调制器失调下的大视场猫眼回波特性分析

段帅军,樊桂花,张来线,刘瑞丰

(航天工程大学电子与光学工程系,北京 101416)

1 引 言

猫眼效应是指入射光束经过猫眼光学系统后能够按照入射方向原路返回发射端,其反射光强度远远高于漫反射[1-3]。基于猫眼效应的逆向调制激光通信系统通过把空间光调制器和猫眼光学系统组合成猫眼逆向调制器,其相对于其他逆向调制通信系统,其能够进一步减小调制器的尺寸,有效提高通信速率[4-7]。但在实际应用中猫眼逆向调制通信系统一般为非理想状态,存在调制器失调、非正入射等情况,这会对通信系统的性能产生严重的影响,因此分析调制器失调和光束非正入射对猫眼回波功率分布的影响有着重要的意义。

本文把猫眼光学镜头的角失调量转换为线失调量,在激光大角度斜入射条件下应用柯林斯衍射积分公式,将含有硬边光阑的光学窗口函数展开为有限个复高斯函数之和,同时考虑了调制器失调的情况,得到了调制器失调情况下的猫眼回波光场分布的解析解,仿真分析和实验验证了调制器俯仰角和入射角的关系以及对回波功率分布的影响。

2 模型建立

一般情况下,猫眼逆向调制通信链路的发射端与逆向调制端距离较远,进入猫眼镜头的光束认为是平行光。将倾斜光束通过猫眼光学镜头的过程展开,把猫眼光学镜头的角失调量转化为线失调量,可得到如图1所示的一个双透镜等效简化模型。其中设立xyz坐标系如图1所示,将z轴设定为主光轴方向,其方向与入射光方向一致。L1为发射端到透镜1前镜面的距离,L2为透镜2后镜面到接收端的距离,θx、θy为入射光束在x和y方向的入射角,φx、φy为调制器在x和y方向的失调角,定义图中θy和φy的取值符号为正。Δx和Δy为光束在等效透镜2前的离轴量,其表达式为式(1)所示。

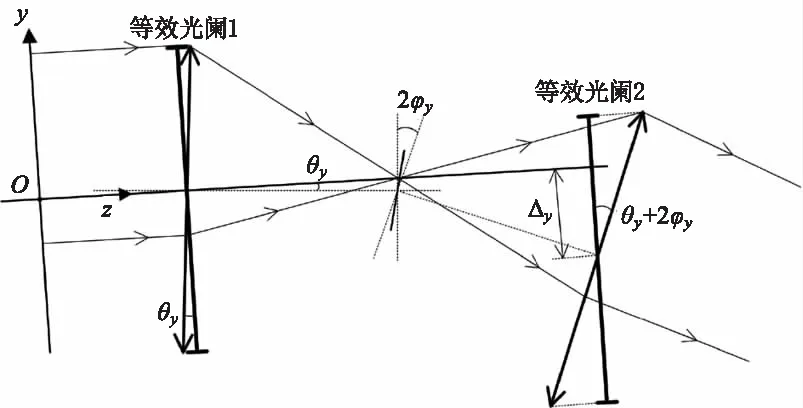
图1 斜入射光束通过调制器失调猫眼镜头的传输过程

(1)

其中,f为透镜的焦距;δ为离焦量。

将激光的传输过程分为三个区间:输入端到等效透镜1前镜面、等效透镜1前镜面到等效透镜2前镜面、等效透镜2前镜面到接收端,其中后两个区间均带有硬边光阑。三个区间的传输矩阵可参考文献[3]。

由于光束存在入射角以及调制器存在俯仰角使得猫眼光学镜头在xyz坐标系下产生倾斜,两个透镜的等效光阑形状为椭圆,在x-y坐标系下,将两个椭圆硬边光阑的窗口函数展开为有限个复高斯函数之和[8],可以写为:

(2)

(3)

其中,Fm、Fn和Gm、Gn分别为式(2)、式(3)展开的复高斯函数之和的展开系数和复高斯函数系数。

设入射激光的束腰位置为输入参考面,则束腰半径为ω0的高斯光束在输入参考面的光场分布为:

(4)

假设焦平面处调制器的尺寸足够大,根据激光区间传输矩阵[3]和式(2)(3)(4),代入到直角坐标系下的柯林斯衍射积分公式[9],并利用化简公式:

(5)

经过一系列的计算,可得输出参考面的光场分布为[3]:

exp{ik[L1+K(1+T)(f+δ)+L2]·

(6)

式中:

(7)

(8)

(9)

(10)

(11)

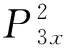
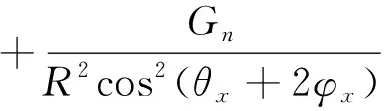
(12)

(13)

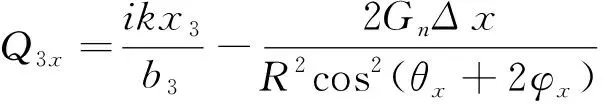
(14)

(15)

输出参考面的光强分布可由下式得到:

(16)

3 仿真分析

通过式(16)可以计算得到输出参考面上猫眼回波的功率分布,在仿真计算中令入射激光的波长为1064 nm,束腰半径为1 mm,猫眼透镜的口径半径为2 cm、焦距为13 cm。因为猫眼逆向调制光学系统为圆对称系统,因此只需考虑入射光束沿y轴方向斜入射的情况,即θx=0。

3.1 调制器俯仰角对回波的影响

为保证输入光束接近平行光,令L1=2 km,L2=10 m,图2、3、4分别是入射角为0°、2°、-2°情况下不同调制器俯仰角的回波光场分布。图中的回波光斑均产生了明显的衍射现象,且光斑的形状为两等效光阑交汇的形状。图2正入射情况下随着调制器俯仰角的逐渐增大,回波光斑逐渐变小,光强值逐渐减小,光斑位置向y轴负方向偏移,衍射峰的数量先增加后减小。图3入射角度为2°时,相比于图2正入射,相同调制器俯仰角对回波产生的影响更大,入射角对俯仰角有一定的“促进”作用,当俯仰角为6°时,俯仰角接近于最大值,光斑形状迅速变小,接近于一条直线,此时衍射最为剧烈。图4入射角度为-2°时,相比于图2正入射,相同调制器俯仰角对回波产生的影响更小,入射角对俯仰角有一定的“抑制”作用,当入射角为-2°,俯仰角为2°,即两者取值互为相反数时,此时的回波光强分布与图2正入射俯仰角为0°时的十分相似,光斑形状均为正圆。

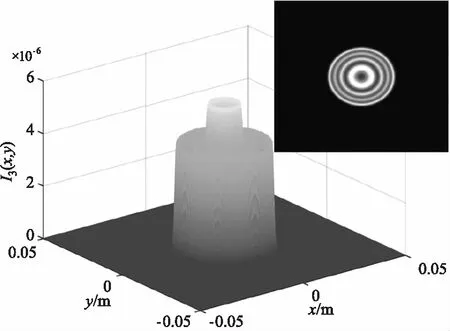
(a)0°

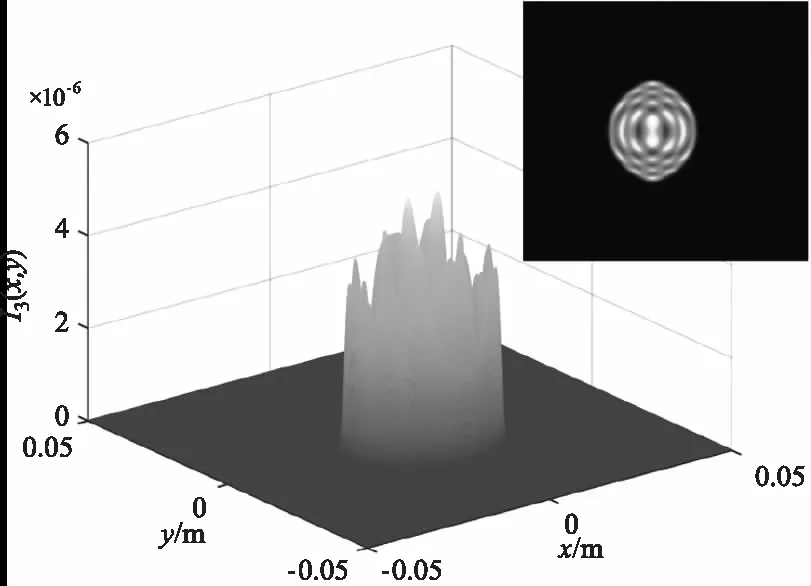
(b)2°

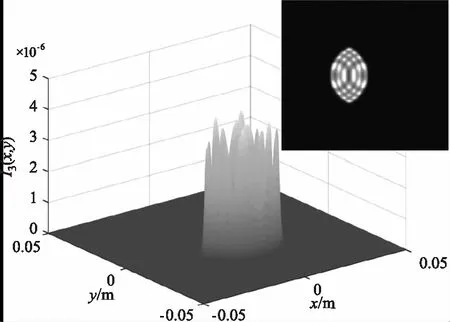
(c)4°

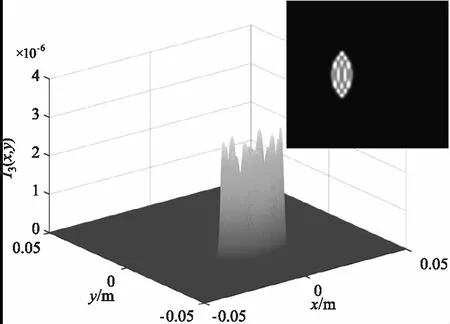
(d)6°

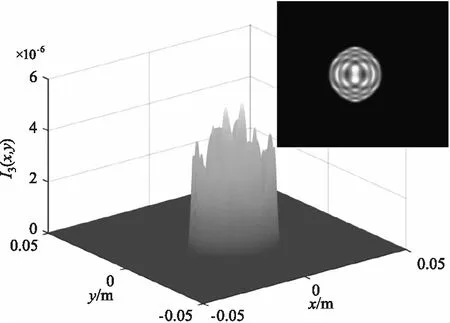
(a)0°

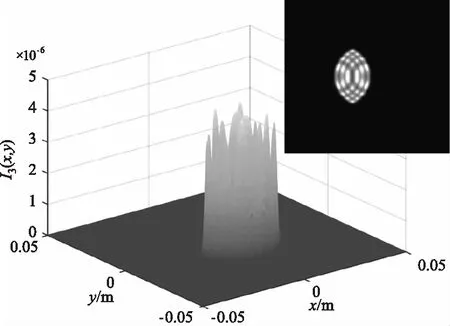
(b)2°

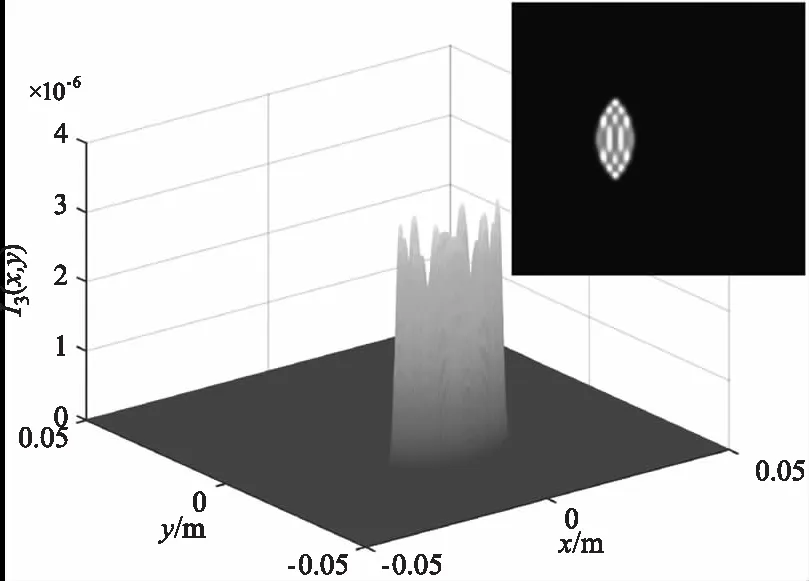
(c)4°

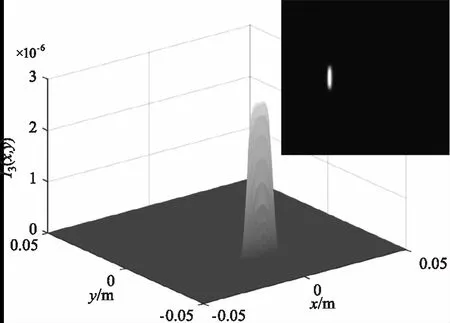
(d)6°

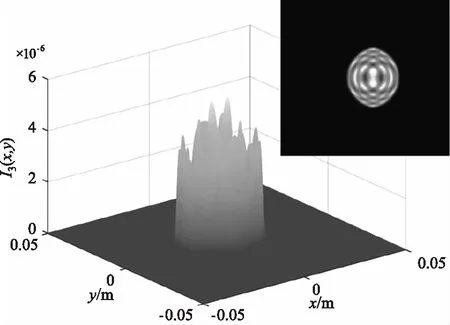
(a)0°

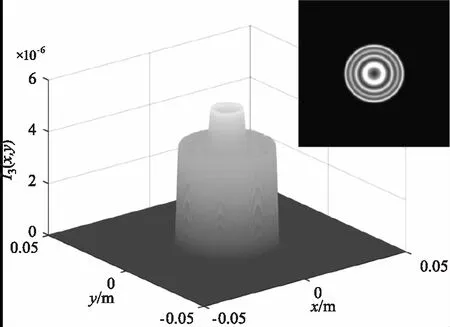
(b)2°

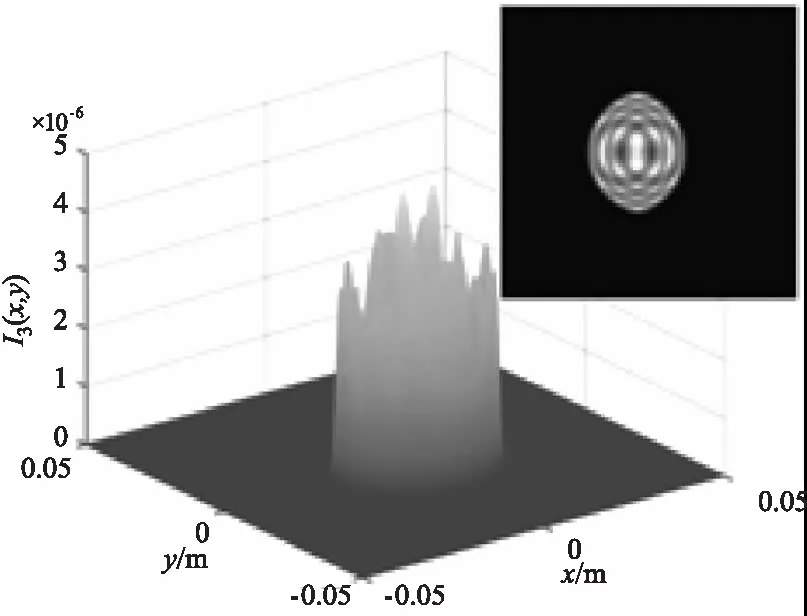
(c)4°

(d)6°

3.2 俯仰角与入射角的关系

在上一节中发现光束入射角与调制器俯仰角之间存在一定约束关系,两者相互影响。因此结合图1,推导出在满足产生回波的前提下,光束入射角和调制器俯仰角遵循以下约束条件:

(17)

由式(17)可得出不同条件下的俯仰角与入射角之间的关系。图5是不同的口径焦距下最大调制器俯仰角与入射角之间的关系,由图5可以看出调制器的最大俯仰角与入射角成反比关系。两者取值符号相同时,入射角越大,最大俯仰角越小；两者取值符号不同时,入射角越大,最大俯仰角越大。同时还发现猫眼的口径越大、焦距越短,入射角固定的情况下最大调制器俯仰角就越大。

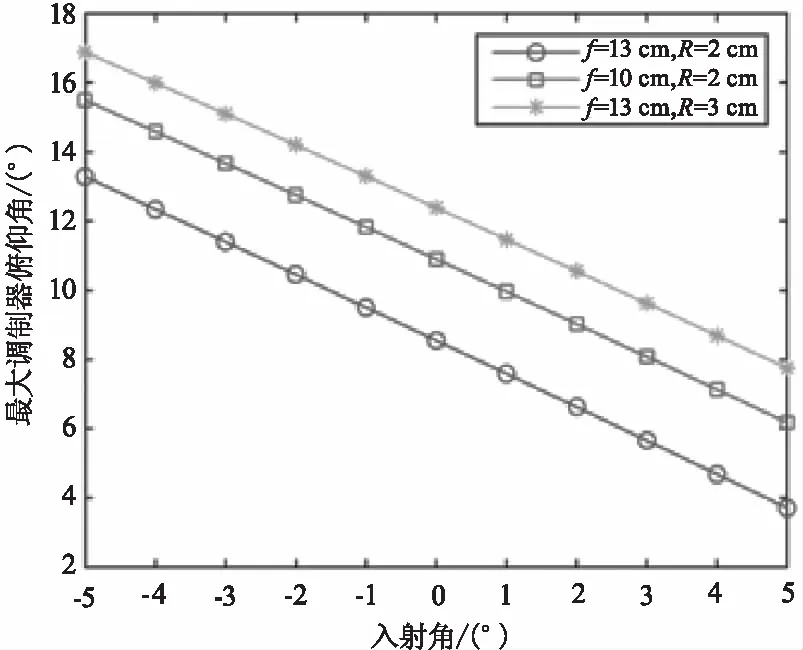
图5 不同的口径焦距下最大调制器俯仰角与入射角之间的关系

图6是不同的口径焦距下最大入射角与调制器俯仰角之间的关系,两者关系类比于图5的分析,最大入射角与调制器俯仰角成反比关系,两者取值符号相同时,俯仰角越大,最大入射角越小；两者取值符号不同时,俯仰角越大,最大入射角越大。同时猫眼的口径越大、焦距越短,调制器俯仰角固定的情况下最大入射角就越大。

4 实验验证

采用实验装置如图7所示。半导体激光器发射激光,经过准直扩束镜、分束镜后到达猫眼光学系统,返回的光束再次经过分束镜在接收屏上产生光斑,光斑图像经摄像机采集送至计算机进行处理。猫眼光学系统由透镜和平面反射镜组成,其中平面反射镜放置在转台1上来实现调制器失调量的改变,整个猫眼光学系统放置在转台2上来实现光束入射角的改变。实验装置的主要参数如下:激光器输出波长为532 nm,分束镜分束比为1∶1,猫眼光学系统半视场角为8.7°,其中透镜口径为40 mm,焦距为130 mm,接收屏和激光器与猫眼光学系统的距离均为10 m。

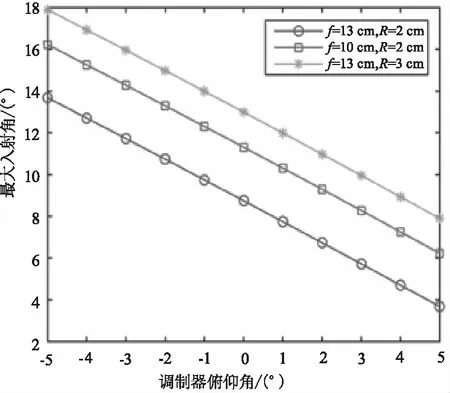
图6 不同的口径焦距下最大入射角与调制器俯仰角之间的关系

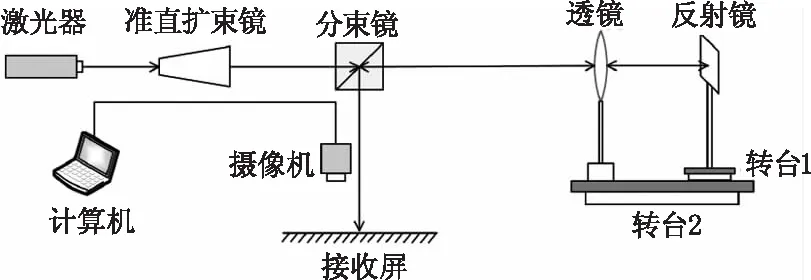
图7 实验装置示意图

为了更好地观测光斑的形状,接收屏上为1 cm×1 cm的网格。图8、图9、图10为入射角分别是0°、-2°、2°时不同调制器俯仰角对应的回波光斑图。由图可得,正入射时回波光斑的形变程度随着调制器俯仰角的增大而加剧,俯仰角互为相反数时对应的回波光斑形状相同。入射角与俯仰角取值符号相同时,回波光斑的形变程度加剧；入射角与俯仰角取值符号相反时,回波光斑的形变程度减弱。当入射角为2°、俯仰角为4°以及入射角为-2°、俯仰角为-4°时回波光斑的形变程度最为剧烈；当入射角为2°、俯仰角为-2°以及入射角为-2°、俯仰角为2°时回波光斑为正圆,与图8正入射调制器非失调的光斑图相同。实验结果与仿真分析较为吻合,区别在于实验光斑的衍射现象强于仿真所得,衍射条纹十分密集,原因是实验中的猫眼光学系统由透镜和反射镜组成,轴外像差比较大。

图8 入射角0°时俯仰角分别为-4°、-2°、0°、2°、4°的回波光斑

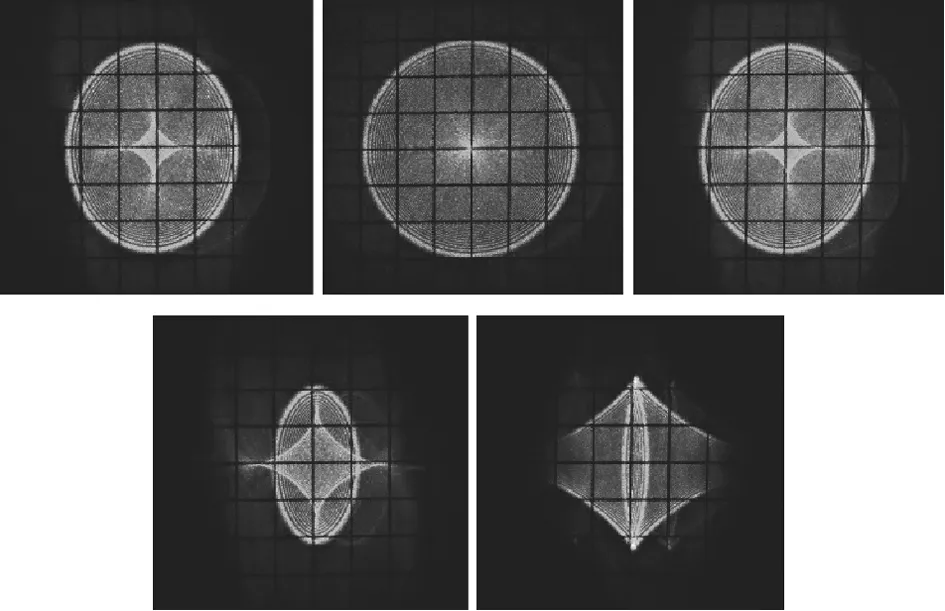
图9 入射角2°时俯仰角分别为-4°、-2°、0°、2°、4°的回波光斑

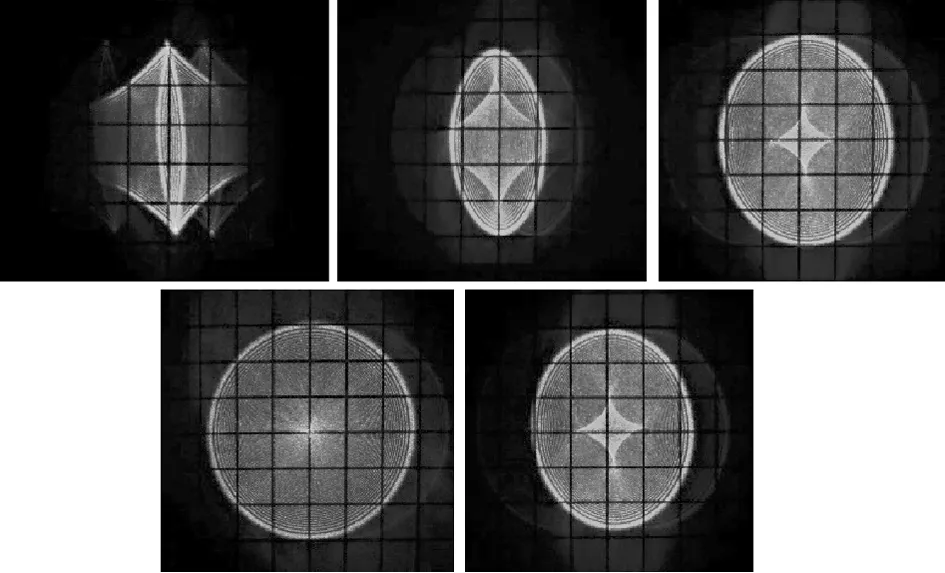
图10 入射角-2°时俯仰角分别为-4°、-2°、0°、2°、4°的回波光斑

固定激光入射角为定值,逐渐调整转台1缓慢增大调制器俯仰角同时观察接收屏回波光斑形状,当光斑形状接近于直线将要消失时记录此时转台旋转的角度为当前入射角取值的最大调制器俯仰角,得到最大调制器俯仰角和入射角的关系如图11所示。由图可得仿真值与实验值基本吻合,最大调制器俯仰角和入射角成反比关系。

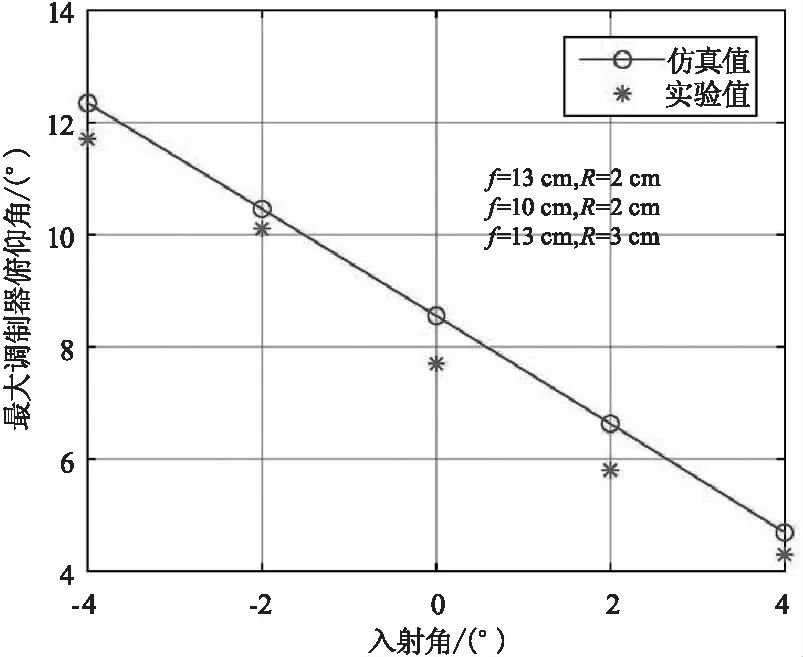
图11 最大调制器俯仰角与入射角的关系

5 结 论

本文将猫眼光学镜头的角失调量转换为线失调量,基于柯林斯衍射积分公式建立了调制器失调下的大视场猫眼回波分布模型,并仿真分析和实验验证了调制器失调量和入射角对回波功率分布的影响。结果表明,若调制器俯仰角和入射角取值符号相同,则两者对回波的影响互相起“促进”作用；若两者取值符号不同,则两者对回波的影响互相起“抑制”作用；若两者互为相反数,则两者对回波的影响互相抵消,等效于正入射调制器非失调状态。猫眼逆向调制激光通信系统一般为非理想状态,利用这一结论可以通过改变系统的入射角或者调制器角失调量,来改善系统的回波质量,提升系统的通信性能。