兰州地铁地温分布特性及其演化规律
2020-04-08张虎元朱江鸿马国梁甄作林盖玉玺
张虎元,朱江鸿,马国梁,甄作林,3,盖玉玺
(1.兰州大学 土木工程与力学学院, 甘肃 兰州 730000;2.兰州大学 西部灾害与环境力学教育部重点实验室,甘肃 兰州 730000;3.中铁西北科学研究院有限公司, 甘肃 兰州 730000)
地铁地温是地铁暖通空调系统优化设计的主要参考指标[1-3],合理设计地铁暖通空调系统,高效节能地调节地下空间的温度[4-5],对于提高乘客的舒适度,节约地铁运营成本具有重要的实际意义。
关于地温的研究已有不少成果,主要集中在地热学,包括矿井围岩地温、地源热泵与地温关系、气象学等[6-9]。其中,针对地铁地温研究较少,只有一些文献针对南京和西安等地的地铁进行了研究,积累了一些数据。Xiang等[10]在分析地铁地温过程中,只给出了恒温层的温度为20 ℃。胡增辉等[11-12]实测了南京地铁地温,运用反演公式计算得到了地层土体的导热系数,并采用数值模拟的手段分析围岩传热范围的影响因素,探究了地铁隧道围岩的传热机理。任建喜等[13]在西安地铁沿线4个典型地貌单元布置9个钻孔,观测得到了不同地貌单元地层的恒温层位置和地层地温的分布规律,为西安地铁暖通空调系统初步设计提供参考。
兰州地铁,处于我国西北高海拔的黄土高原地区,其所在地层与我国其他地方的地铁地层不同。目前,关于兰州地铁地温的分布规律研究相对缺乏。确定兰州地铁初始地温(隧道开挖前的地温)及运营条件下兰州地铁系统与初始地温的相互作用规律,为今后兰州地铁运营过程中暖通空调的优化提供可靠的参考依据,可为高海拔地区地铁空调工程的初步设计提供参考。因此,本文实测兰州地铁所在地层全年的初始地温,分析其变化规律,提出兰州地铁初始地温预测模型公式;并采用非稳态传热的数值模型,探究运营条件下兰州地铁围岩温度演化规律。
1 工程概况和现场监测方法
1.1 工程概况
根据兰州市城市规划和轨道交通线网规划,兰州地铁分布在兰州盆地内部的河谷地带,由河谷高阶地和河谷平原组成,地貌上属于侵蚀—堆积河谷平原。地形较为平坦,其中包括黄河Ⅰ—Ⅳ级阶地和漫滩。
兰州地铁沿线分布的围岩地层主要有第四系全新统杂填土、素填土、黄土状粉土、粉质黏土、粉细砂和下更新统卵石地层。土层一般为可塑—软塑状态,砂层稍密—密实,潮湿—饱和,卵石层稍密—中密,地层稳定,可作为围岩和地基持力层,场地土的类型多为中硬场地土,部分为中软场地土,场地类型为Ⅱ类。
1.2 监测断面及测点布置
初始地温监测断面位于甘肃省兰州市兰州西客站(兰州地铁沿线重要车站之一)附近,与隧道水平距离为50 m左右,以保证地铁隧道施工过程对监测地温无影响,海拔高程为1 524.36 m。
根据地铁隧道底板埋深为19.5~21.8 m,测点的最大深度设置为23 m。从地表开始,往下每隔1 m设置1个测点,测点埋深依次为1,2,3,…,23 m,命名依次为T1,T2,T3,…,T23,如图1所示。

图1 地温测点布置(单位:m)
1.3 监测时间
监测从2017-03-25开始,至2018-03-17停止,共1年,测量周期为7 d·次-1。这1年4个季节的起止时间为:春季,2017-03-21—2017-06-20;夏季,2017-06-21—2017-09-22;秋季,2017-09-23—2017-12-21;冬季,2017-12-23—2018-03-20。
1.4 监测仪器
地温监测仪器主要有温度传感器、温度采集仪器,如图2所示。温度传感器是自制的,由1/3B级JUMO四线制pt100铂热电阻、四线制四氟屏蔽导线、温度探头和插头组成,精度为0.01 ℃,具有耐250 ℃高温、耐-50 ℃低温、耐腐蚀的功能,见图2(a)。每个测点埋入1个温度传感器的探头。温度采集仪器采用wKc-988数字测温仪,见图2(b),测温范围为-20~100 ℃,分辨率为0.1 ℃。

图2 监测仪器
1.5 仪器校准
为了保证温度测量的准确性,所有温度传感器在埋设之前进行温度校准。在正式测量初始地温之前,在冬季时测量了兰州地铁埋深1 m处的初始地温,发现最低值大于0 ℃,并且兰州环境气温不会超过50 ℃,则校准范围为0~50 ℃。在温度校准时,0~15 ℃的温度环境在DW-40L262低温冷藏箱进行,15~50 ℃的温度环境在SHZ-88水浴恒温震荡器进行,低温冷藏箱和水浴震荡器的温度通过多个温度计验证,准确性良好。图3所示为温度传感器的室内温度校准曲线,横坐标实际温度为低温冷藏箱温度或水浴温度,纵坐标测量温度为温度采集仪器测试温度传感器的读数。从图3可以看出,测量温度与实际温度具有良好的线性关系,测量温度=实际温度+四线制四氟屏蔽导线的长度×0.3。测量温度与实际温度之间的误差是由四线制四氟屏蔽导线的电阻造成的,是不可避免的[14-16]。因此,现监测得到的地温数据,需要通过室内温度校准曲线(图3)进行校正,校正后的数据才是监测位置的真实温度。
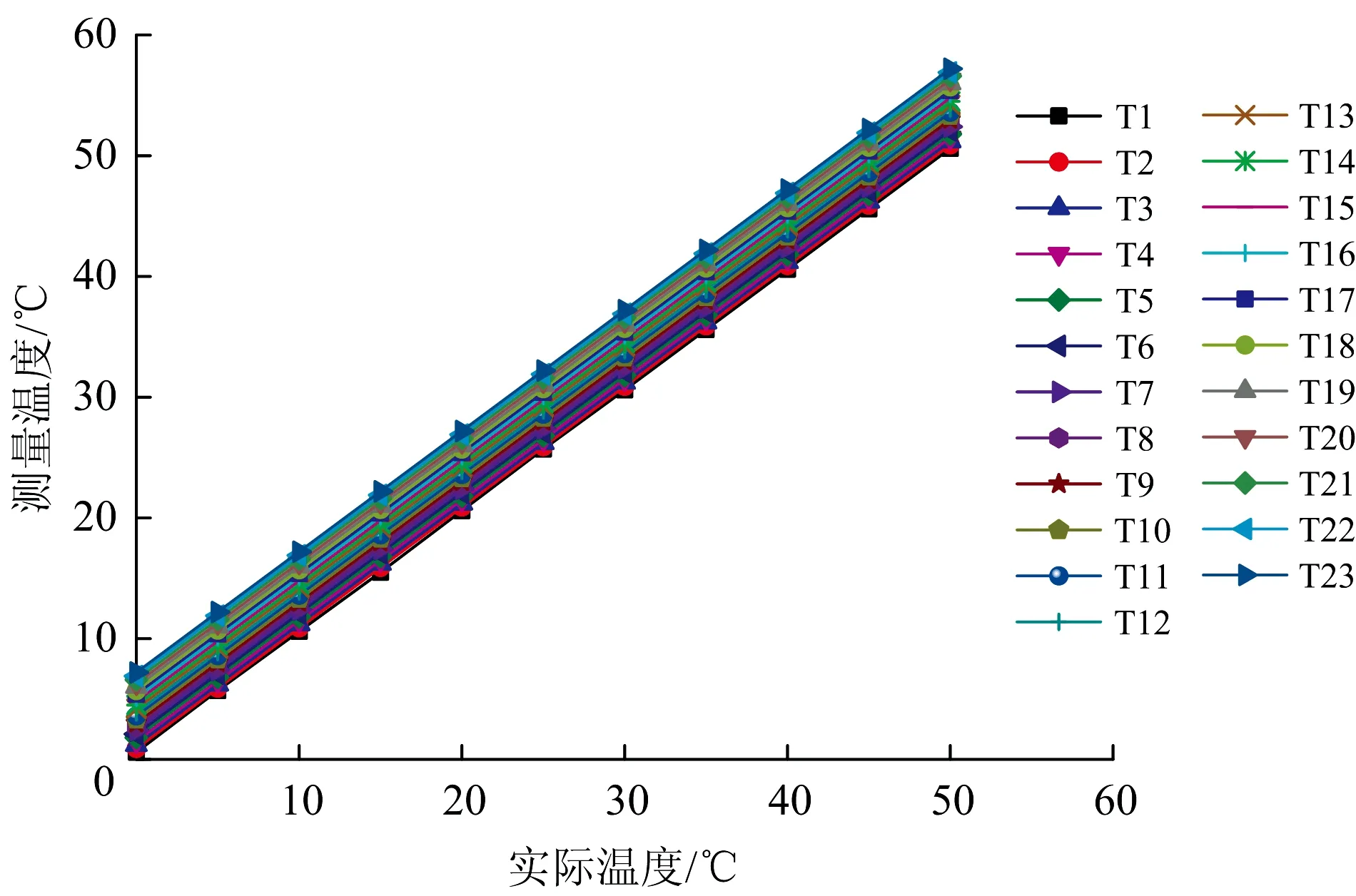
图3 温度传感器室内温度校准曲线
2 初始地温监测结果
2.1 环境气温分布规律
环境气温不同,则地铁初始地温不同,并且不同深度的初始地温随着环境气温的变化会表现不同的变化规律,因此,应先分析环境气温的变化规律。
不同季节日平均气温随时间的变化规律如图4所示,图中横坐标轴时间表示1个季节从头至尾的依次天数。从图4可以看出:在春季,日平均气温整体呈上升趋势,最初的日平均气温为10 ℃左右,最后的日平均气温可达到23 ℃左右,季平均气温为16.5 ℃;在夏季,日平均气温刚开始整体呈上升趋势,最高可达31 ℃,然后呈下降趋势,最末在18 ℃左右,季平均气温为22.8 ℃;在秋季,日平均气温整体呈下降趋势,范围在-3~19 ℃,季平均气温为6.9 ℃;在冬季,日平均气温整体呈现下降、上升、再下降(最低可达-10 ℃)、然后再上升的趋势,最末在13 ℃左右,季平均气温为0.4 ℃。
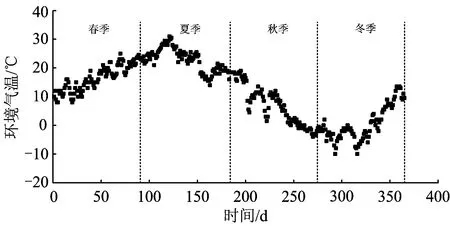
图4 不同季节日平均气温随时间的变化规律
2.2 不同季节地铁初始地温分布规律
兰州地铁1年4个季节初始地温随埋深的变化规律如图5所示。结合图5和图4可以发现初始地温与环境气温、埋深的关系,以及其平均值的分布规律,分别如下。

图5 兰州地铁初始地温随埋深的变化规律
1) 初始地温与环境气温的关系
地表至埋深5 m段内,初始地温受环境气温的影响较为明显,随着环境气温的变化而发生变化。埋深5 m至埋深12 m段内,初始地温受环境气温的影响相对于前一范围更不明显。埋深12 m至埋深23 m段内,初始地温受环境气温的影响最小,在整个时节中随时间的变化幅度小于0.3 ℃。可见,埋深越大,初始地温受环境气温影响越小。
埋深1 m处的初始地温:在春季,从10.8 ℃增大到19.8 ℃,增幅超过9 ℃;在秋季,减幅超过10 ℃,从22 ℃一直下降到11.9 ℃;在冬季,变幅超过5 ℃,最高可达11.5 ℃,最低可达4.9 ℃。每1个测点的初始地温在各个时节中变化幅度均超过4 ℃。
2) 初始地温与埋深的关系
地表至埋深12 m段内,随埋深的增大,春季中,3月25日和4月1日的初始地温都呈增大的趋势,4月8日至6月17日的初始地温都呈先减小后增大的趋势;夏季中,6月24日至7月15日的初始地温都呈先减小后增大的趋势,7月22日至9月16日的初始地温都呈减小的趋势;秋季中,9月23日至10月14日的初始地温都呈减小的趋势,10月21日至12月16日的初始地温都呈先增大后减小的趋势;冬季中,初始地温都呈先增大后减小的趋势的趋势。
埋深12 m至埋深23 m段内,随埋深的增大,4季中初始地温的变化幅度均较小,春季和夏季小于0.3 ℃,秋季和冬季小于0.4 ℃。
3)初始地温平均值的分布规律
初始地温平均值随埋深的变化规律如图6所示。由图可知:地表至埋深12 m段内,随埋深的增大,春季初始地温平均值呈先增大后减小的趋势,夏季初始地温平均值呈减小的趋势,秋季初始地温平均值呈先增大后减小的趋势,冬季初始地温平均值呈增大的趋势,全年初始地温平均值呈先增大后减小的趋势;埋深12 m至埋深23 m段内,随埋深的增大,春、夏、秋、冬和全年初始地温平均值的变化幅度均较小,小于0.4 ℃。

图6 兰州地铁初始地温平均值随埋深的变化规律
地表至埋深3 m段内,初始地温平均值从大到小的顺序是夏季、秋季、全年、春季、冬季。埋深3 m至埋深12 m段内,初始地温平均值从大到小的顺序是秋季、夏季、全年、冬季、春季。埋深12 m至埋深23 m段内,春、夏、秋、冬和全年初始地温平均值均在15 ℃左右。
由此可知,兰州地铁地层的初始地温,年变温层为地表至埋深12 m(不包含12 m);年恒温层为埋深12 m及其以下,温度为15 ℃。
2.3 年变温层中初始地温分布规律
年变温层中,埋深1,2,…,11 m处初始地温的时程曲线如图7所示。图中横坐标轴时间的1表示2017年3月21日,即春季的第1天,之后依次累加;本研究第1次温度监测日期是2017-03-25,为第5天,其他监测日期的表达方式类似。从图7可以看出,在初始地温的年变温层中,各埋深处的初始地温年变化规律与环境气温变化规律相似,近似呈正弦曲线状分布。
根据图7每1个测点初始地温的最大值和最小值,计算差值得到振幅,初始地温的振幅随埋深的变化规律如图8所示。由图8可知:1年中初始地温的振幅随埋深的增大逐渐减小。埋深为1 m时,1年中初始地温的振幅大于18 ℃;埋深为11 m时,1年中初始地温的振幅小于1 ℃。初始地温的振幅与埋深呈指数关系。

图7 兰州地铁年变温层中不同埋深的初始地温时程曲线

图8 兰州地铁初始地温振幅随埋深的变化规律
结合图7和图4可知:随埋深的增大,1年中初始地温的变化曲线存在初始地温滞后于环境气温的现象,则环境气温对初始地温的影响不是即时的而是有一定的滞后性。埋深1 m处,1年中初始地温最高时日期是8月26日;随着埋深逐渐增大,1年中初始地温最高时日期逐渐往后推;到了埋深11 m处,初始地温最高时日期是11月11日。1年中初始地温最低时日期的变化规律与最高时相似。
3 初始地温预测模型公式
以监测兰州地铁初始地温的数据为基础,提出兰州地铁初始地温预测模型公式,以解析解的形式反映兰州地铁初始地温。
3.1 地温预测模型公式
3.1.1 变温层
假定变温层是均一介质,地层在深度方向的传热远大于在水平方向的传热,基于傅里叶定律,可以得到一维传热方程表示的变温层地温[17]为
(1)
式中:T(z,t)为第t天深度z处的地温, ℃;z为埋深,m;t为距离起算日期的时间,d;K为导热系数,W·(m·K)-1。
地表处的地温为[17]
T(0,t)=D0+A0sin(2πft+β)
(2)
式中:D0为地表处平均地下, ℃;A0为地表处地温年变化幅值, ℃;f为频率,1年365天,即可取1/365;β为初相角。
基于式(1)和式(2),可求解得[17]

(3)
式中:a0为地表处的导温系数,m2·d-1。
然而,兰州地铁的变温层并不是同一介质,而是由多种介质构成的,不同介质的D,A,a均不相同,因此需对式(3)进行改进。对于同一介质的地层,地温Ts(z,t)为
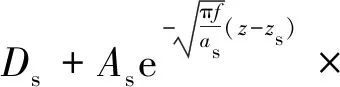
(4)
式中:Ds为同一介质地层的顶面处平均地温, ℃;As为同一介质地层的顶面处地温年变化幅值, ℃;as为同一介质地层的导温系数,m2·d-1;zs为同一介质地层的顶面处深度,m;ts为同一介质地层中距离起算日期的时间,d。
3.1.2 恒温层
在恒温层中,地温保持不变,设恒温层的地温为Th(℃),则地温可表示为
T(z,t)=Th
(5)
3.2 兰州地铁初始地温预测模型公式的构建与验证
3.2.1 变温层
在初始地温中,兰州地铁年变温层自上而下依次由杂填土、素填土、黄土状粉土、粉质黏土、粉细砂等组成,共5种介质。在钻孔时对5种介质的地层分别取样,并采用Hot Disk TPS2500s热常数分析仪测试其热物理参数,可得5种介质地层的as;根据每个测点的年平均初始地温,按照相对的范围对其进行线性内插可得各个介质地层的Ds,其中地表年平均初始地温,与恒温层初始地温相等[18],为15.00 ℃;各介质地层的As通过图8的拟合函数可得;各介质地层的βs通过该层的任意1个温度监测数据(图8的坐标点)便可确定;由此得到各介质地层Ds,As,as,βs参数的取值见表1。
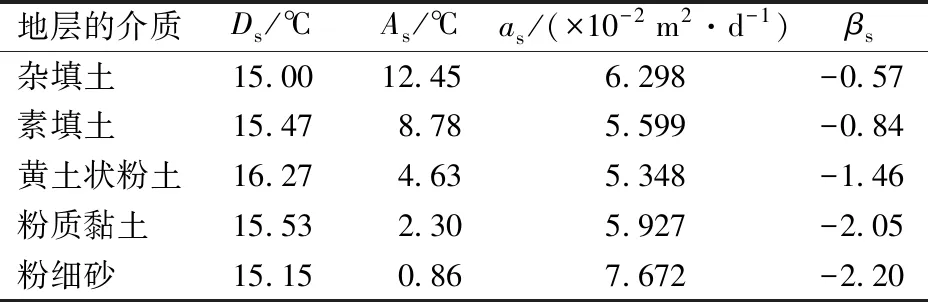
表1 模型参数的取值
z取1,2,3,…,11,对应图1的地层范围确定地层的介质,根据地层介质在表1中选取模型参数的值,代入式(4),得到11个式子,这11个计算公式就是兰州地铁初始地温预测模型公式,分别命名为式(6-1)、式(6-2)、式(6-3),…,式(6-11)。采用该预测模型公式预测2017-03-25至2018-03-17的兰州地铁初始低温地温时程曲线,如图9所示。对11条曲线分别进行拟合,其R2都大于0.85,说明采用该模型可以较为准确地预测兰州地铁初始地温预测。

图9 预测的兰州地铁变温层中不同埋深的初始地温时程曲线
3.2.2 恒温层
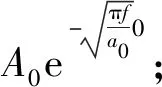
(7)
根据式(7)可求得
(9)

4 运营条件下兰州地铁隧道围岩温度演化规律
根据兰州地铁初始地温的监测数据和预测模型公式,再运用非稳态传热的数值模型,模拟计算兰州地铁运营过程中隧道内空气与围岩之间热交换形成的围岩温度,探究地铁运营条件下围岩温度的演化规律。
4.1 围岩温度非稳态传热数值模型的建立
4.1.1 控制方程
热存储项的计入将稳态系统转变为非稳态系统,非稳态传热分析的控制方程为[19]

(10)
式中:C为比热容矩阵;T为围岩温度或者隧道内环境温度向量;K为导热系数矩阵;Q为热流率向量。
在非稳态传热分析中,热流率随时间变化时,非稳态传热分析的控制方程为[19]
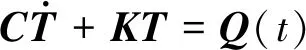
(11)
采用有限元分析软件Ansys,对方程式(11)求解,得到隧道内不同环境温度时的地铁隧道的围岩温度。
4.1.2 隧道模型
地铁隧道底板埋深设计是19.5~21.8 m,且周围土体为卵石土。设置隧道模型均处于恒温层中,整个隧道模型的初始围岩温度为15 ℃,隧道模型的上下边界与左右边界条件均一致。参考兰州地铁隧道设计尺寸,将模型中的地铁隧道断面设为圆形,半径为2.7 m,衬砌厚0.6 m,与围岩直接接触。隧道模型圆心为点(0, 0),设圆心距离隧道模型顶面(恒温层底面)为8 m,圆心距离隧道模型底面为27 m,圆心距离隧道模型左面和右面都为27 m。隧道模型单元的边长为0.1 m。
4.1.3 围岩温度非稳态传热数值模型的地层介质物理参数
采用Hot Disk TPS2500s热常数分析仪测试兰州地铁卵石土和混凝土衬砌的热物理参数,结果见表2。围岩温度演化过程主要靠隧道内空气与衬砌围岩之间产生的对流进行热交换,隧道壁面的换热系数为10.0 W·(m2· ℃)-1 [20]。

表2 围岩与支撑结构的热物性参数
4.1.4 围岩温度非稳态传热数值模型的模拟工况
地铁围岩温度演化过程主要考虑的影响因素有:地铁运营时长,隧道内环境温度、围岩初始温度、围岩及衬砌的热物理参数。其中,围岩初始温度、围岩及衬砌的热物理参数均已确定。
根据《地铁设计规范》[21],在空调调控中,地铁隧道内环境温度最高不应高于30 ℃,最低应等于当地地层的自然温度,同时最低不应低于12 ℃。因此,设定隧道内环境温度分别为20,25和30 ℃(没有考虑通风风速),探究隧道内不同环境温度时随着地铁建成时间的增加地铁隧道围岩温度的演化规律。
4.2 数值模型有效性验证
以胡增辉的地铁隧道模型试验参数[11]为基础,运用Ansys及控制方程[19],建立胡增辉的地铁隧道模型的数值模型,初始围岩温度取15.8 ℃,隧道内温度取地铁设计的隧道内环境极限温度35 ℃。采用胡增辉地铁隧道模型试验得到的距洞壁不同距离处不同热交换时间时围岩温度的实测值[11]与采用本文预测方法得到的预测值进行对比,见表3。从表3中可以看出,预测值在实测值的5%误差以内,误差较小,验证了本文预测方法的合理性和有效性。
4.3 数值模拟结果及分析
4.3.1 围岩温度分布云图
随着地铁建成时间的增加隧道围岩温度分布云图如图10所示。由图可知:隧道内空气与围岩之间热交换1个月后,隧道围岩温度等温线以同心圆形态分布,围岩温度大于16 ℃的面积不到数值模型总面积的1/10;热交换6个月后,隧道围岩有一部分温度等温线分布形态开始呈扁圆形;热交换5年后,等温线基本呈扁圆形,围岩温度大于16 ℃的面积约是数值模型总面积的1/2;随距隧道内壁距离的增大,围岩温度等温线间距呈增大的趋势,说明距离隧道内壁越远,围岩温度梯度越小,围岩温度变化幅度相对更小。
表3 距洞壁不同距离处不同热交换时间时围岩温度的实测值与预测值对比

距洞壁的距离/cm12 h后围岩温度/℃20 h后围岩温度/℃实测值预测值实测值预测值130.830.231.030.4229.228.729.529.3427.726.528.027.6726.025.126.825.51123.022.124.023.41621.020.122.221.72219.818.321.020.42918.317.920.019.23718.017.519.318.9

图10 隧道围岩温度分布云图(单位:℃)
4.3.2 隧道内环境温度对围岩温度分布的影响
取自隧道拱顶向上至数值模型边界的线为A线,自隧道右侧壁且坐标y=0处向右至数值模型边界的线为B线,自隧道仰拱中点向下至数值模型边界的线为C线。
3条线上隧道围岩温度的分布规律如图11所示。由图可知:围岩温度与距隧道内壁距离成负相关关系;以C线的温度为例,隧道内环境温度相同时,随热交换时间的延长,同一位置处的温度逐渐增大,图中曲线的斜率逐渐增大,即温度梯度呈增大的趋势;热交换时间相同时,随隧道内环境温度的增大,同一位置处的温度逐渐增大,温度梯度呈增大的趋势;对于A线和B线,温度及温度梯度随热交换时间或隧道内环境温度的变化规律类似。

图11 隧道围岩温度的分布规律
分析图10,隧道各处的围岩温度及围岩温度梯度分布情况与A线、B线、C线类似。因此,围岩温度及温度梯度与隧道内环境温度、热交换时间均成正相关关系。
热透厚度指隧道内壁与围岩温度稳定处的距离。定义围岩温度变化小于5%处为围岩温度稳定处[11]。以C线为例,热透厚度见表4。由表4可知:隧道内环境温度相同时,随热交换时间的延长,热透厚度逐渐增大;热交换时间相同时,随隧道内环境温度的增大,热透厚度逐渐增大,但是增大幅度呈减少的趋势;热交换时间相同的情况下,隧道内环境温度为30 ℃的热透厚度与隧道内环境温度为25 ℃的热透厚度相差不到0.5 m;对于A线和B线,热透厚度随热交换时间或隧道内环境温度的变化规律类似;结合图10的围岩温度分布云图,热透厚度未达到极限(数值模型边界处温度变化为5%)时,热透厚度与隧道内环境温度成正相关关系,与热交换时间时间成正相关关系。
表4 不同隧道内环境温度时不同热交换时间下的隧道围岩热透厚度(C线)
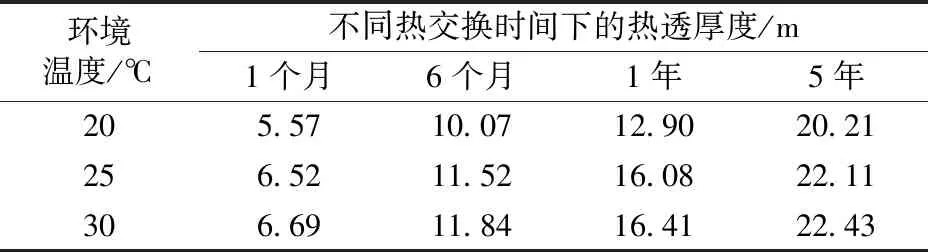
环境温度/℃不同热交换时间下的热透厚度/m1个月6个月1年5年205.5710.0712.9020.21256.5211.5216.0822.11306.6911.8416.4122.43
5 结 论
(1)兰州地铁初始地温,随着环境气温的不同而不同,随着埋深的不同,其变化规律不同;年变温层位于自地表至埋深12 m处;年恒温层位于埋深12 m以下,温度为15 ℃左右。
(2)年变温层中,1年内初始地温变化规律与环境气温变化规律相似,近似呈正弦曲线状分布,但存在相位滞后的现象;1年中初始地温的振幅随埋深的增大呈指数减小。
(3) 基于实测数据,提出兰州地铁初始地温预测模型公式,以解析解的形式反映兰州地铁初始地温。
(4) 在隧道内空气与围岩之间热交换过程中,兰州地铁隧道围岩温度、围岩温度梯度与隧道内环境温度、热交换时间均成正相关关系,与隧道内壁距离成负相关关系。
(5) 在隧道内空气与围岩之间热交换过程中,热透厚度未达到极限(数值模型边界处温度变化为5%)时,热透厚度与隧道内环境温度、热交换时间均成正相关关系。
