32 m高速铁路简支梁桥铺轨后残余徐变上拱限值研究

田新宇，高 亮，刘明辉，蔡小培

(1.北京交通大学 土木建筑工程学院，北京 100044；2.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081)

我国高速铁路大量采用“以桥代路”的方式控制工后沉降和轨道平顺性[1]。简支梁具有结构简单、施工快捷、经济性强等优点[2-4]，高速铁路桥梁目前大量采用32 m跨度预应力混凝土简支梁，同时，无砟轨道也因其高平顺性和少维修性而广泛应用于高速铁路建设。

高速铁路预应力混凝土简支梁因截面长期处于预应力产生的偏心受压状态，易随着时间变化逐渐产生不同的塑性变形，即徐变压缩变形[5-6]。徐变压缩变形量下缘最大，向上逐渐减小，因而导致梁体向上拱起，即徐变上拱[7-8]。无砟轨道直接设置在桥梁之上，梁面一般与底座板固结在一起，而桥梁的竖向刚度远大于轨道板的刚度，桥梁徐变的位移将传递到轨道上。由于钢轨是连续弹性体，在梁缝处不会形成相应的折角，而是形成缓和的弯曲变形过渡[9-11]。对于长大连续等跨简支梁桥地段，从纵断面上看则存在连续的周期性高低不平顺[12-13]。针对混凝土桥梁徐变上拱与无砟轨道协调性及其对高速列车—轨道—桥梁耦合系统动力特性的影响等问题，国内外学者开展了诸多研究。刘鹏等主要分析了混凝土桥梁徐变与无砟轨道不平顺间的映射关系，并探究了桥梁基础上拱对无砟轨道结构受力变形影响的规律[14]；徐庆元[15]、杨宏印等基于车桥耦合动力学理论研究了桥梁徐变上拱条件下车—线—桥结构动力学响应及列车的走行性变化规律。既有研究大多只是定量地分析了桥梁徐变上拱引起的车—轨—线系统的静、动力学行为，尚缺乏对桥梁徐变上拱阈值的关注。受扣件调整量的限制，无砟轨道平顺性对轨下结构变形十分敏感，为保证行车的安全舒适性，需提出桥梁徐变上拱限值以控制混凝土结构的长期变形，确保线路的高平顺性。

本文采用Midas软件建立简支梁—CRTSⅡ型板式无砟轨道有限元模型和车—线—桥耦合动力模型，进行32 m高速铁路简支梁桥铺轨后残余徐变上拱限值研究。

1 桥上无砟轨道周期性不平顺特征

随着铁路向着高铁、重载的方向不断发展，轨道结构的动态检测手段也日趋多样化、精细化。动态检测的最终目的是应用检测结果对轨道质量状态进行评价，以指导线路运维工作。图1—图3分别给出了京津城际(2017年2月7号)、昌福线和杭深线简支梁桥上综合检测列车定期检测数据。

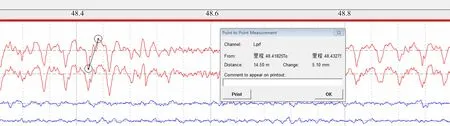
图1 京津城际简支梁桥上实测的无砟轨道高低不平顺

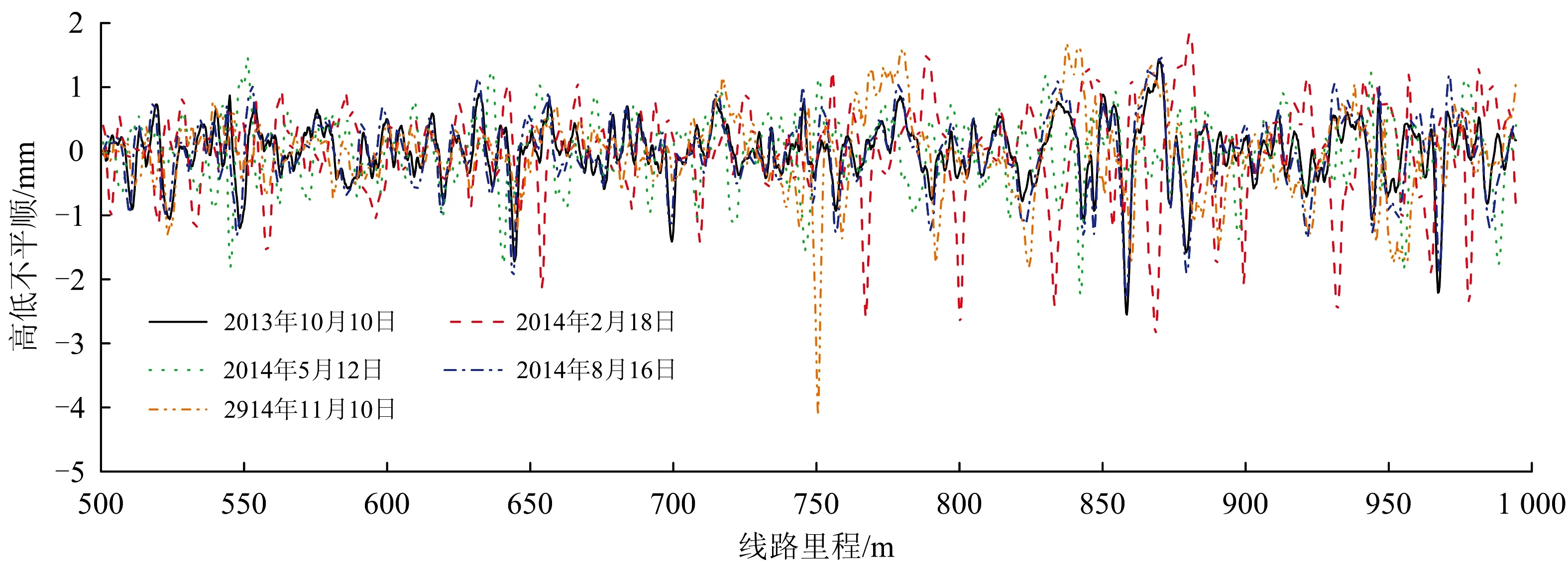
图3 杭深线简支梁桥上实测的无砟轨道高低不平顺

由图1—图3可知，我国京津城际、昌福线和杭深线3条线路上均存在明显的周期性不平顺，其波长与32 m简支梁桥跨度相近，且随运营时间的增加处于持续发展中。进一步分析可知，京津城际典型简支梁桥上跨中—支座的高低不平顺差值为5.1 mm；与此类似，昌福线和杭深线桥上跨中和支座处的高低不平顺差值分别达到了6.4和4.8 mm。

我国相关铁路设计单位针对32 m双线无砟轨道后张法预应力混凝土简支箱梁结构进行了详细的受力计算，并给出了相关的计算结果见表1。

由表1可知：32 m无砟轨道预应力简支箱梁理论计算残余徐变变形量在6.2～7.3 mm，对比上文提到的跨中和支座处高低不平顺的差值可知两者在量值上相差不大。综合上述波长和幅值对比结果，可认为残余徐变上拱是导致桥上周期性轨道不平顺的主要原因。实际工程受铺轨时间和桥梁服役龄期影响，桥梁的徐变上拱值往往不会达到理论计算值。

表1 箱梁受力计算结果

高速铁路混凝土桥梁在长期预应力的作用下，由于混凝土的徐变特性，桥梁有时会出现比较明显的残余徐变上拱，预应力混凝土桥梁残余徐变上拱引起轨面的变形属于静态变形。其存在直接影响了线路的质量指数TQI及车辆、无砟轨道、桥梁结构的服役状态，增大了车辆和桥梁的动力性能。当桥梁残余徐变变形过大时，必将引起线路的动态TQI数据超限。

2 简支梁桥残余徐变上拱与桥上钢轨附加变形的映射关系

桥上轨道结构作为最直接的行车基础，其服役状态与行车品质息息相关。桥梁残余徐变变形会引起无砟轨道长钢轨产生一定的上拱变形，连续布置的简支梁桥则形成周期性的不平顺，直接影响行车的安全舒适性。桥梁—无砟轨道—长钢轨作为一个多层异质结构体系，其传力和承力关系十分复杂，桥梁残余徐变上拱和桥上钢轨附加变形间的映射关系值得关注。

基于有限元软件MIDAS/CIVIL建立15跨32 m简支梁桥上CRTSⅡ型板式无砟轨道无缝线路空间耦合模型，研究混凝土简支梁桥发生残余徐变上拱时，桥上无缝线路长钢轨的附加变形特性。简支梁桥上CRTSⅡ型板式无砟轨道无缝线路自上而下包括钢轨、扣件、轨道板、砂浆层、底座板、“两布一膜”滑动层、“两布”滑动层、剪力齿槽、端刺和桥梁等结构部件，建模时均考虑在内，同时为保证轨面变形的连续性，减少边界条件对模型计算的影响，轨道结构两侧各延伸至桥外100 m。

模型中钢轨采用标准CHN60轨，采用梁单元模拟；轨道板混凝土强度等级为C55，长、宽和厚三向尺寸分别为6.25，2.55和0.20 m，底座板采用C30混凝土，其宽和厚分别为2.95和0.19 m，简支梁、轨道板和底座板考虑其受力特征均采用梁单元进行模拟，桥梁模型参数依据通桥〔2008〕2322A-Ⅵ “时速350公里客运专线铁路无砟轨道后张法预应力混凝土简支梁(双线)跨度31.1 m”确定。扣件垂向阻力、“两布一膜滑动层”、轨道板与砂浆层、砂浆层与底座间纵向的相互作用关系均采用非线性弹簧单元模拟，垂向相互作用关系采用线性弹簧单元模拟。模型中假设简支梁桥墩固定支座完全阻止梁墩间的相对位移，且不考虑活动支座摩阻力，桥梁墩底全约束。

模型参数：扣件间距为0.65 m，纵向阻力无载时取30 kN·m-1·线-1，有载时取60 kN·m-1·线-1，屈服位移取0.5 mm，扣件垂向刚度采用线性弹簧单元模拟，取为35 kN·mm-1。桥上“两布一膜”滑动层和摩擦板上“两布”滑动层的摩擦系数参考规范选取，如图4所示，均为双折线，分析中“两布一膜”滑动层摩擦系数取0.3。模拟轨道板和底座板垂向连接的线性弹簧单元的参数取值根据CA砂浆弹性模量及厚度换算得出。对于底座板和桥梁间的垂向弹簧单元，根据挤塑板的刚度换算得到其参数取值，CRTSII型板式无砟轨道参数见表2。

图4 滑动层摩擦系数取值图

表2 CRTSII型板式无砟轨道参数

研究桥梁残余徐变变形条件下桥上无缝线路长钢轨的附加变形特性时，桥梁的残余徐变变形作为已知的位移边界约束条件施加于桥梁的桥面。建立的双线简支梁桥—无砟轨道—钢轨有限元模型示意图如图5所示。

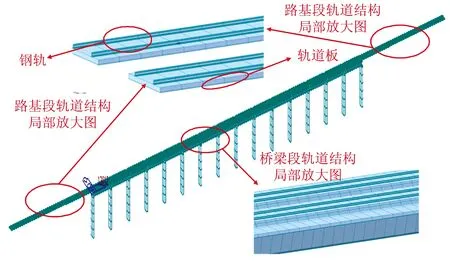
图5 桥上纵连板式无砟轨道无缝线路空间耦合模型

基于上述建立的简支梁桥—纵连式无砟轨道空间耦合模型，考虑铺轨后桥梁分别产生残余徐变变形幅值为3，4，5，6，7，8，9和10 mm的上拱，计算桥梁残余徐变引起的桥上钢轨附加变形。图6给出了残余徐变幅值为10 mm时桥上长钢轨产生的附加变形示意图。

图6 残余徐变幅值为10 mm时引起钢轨附加变形示意图

图7给出了残余徐变幅值分别为3和10 mm时长钢轨的垂向变形。图 8给出了不同残余徐变变形幅值引起的钢轨变形幅值。由图6和图7可知：不同桥梁残余徐变变形条件下，各跨桥上长钢轨的垂向位移分布规律基本相同，钢轨产生的垂向变形关于桥梁跨中对称分布，且最大的垂向变形出现在桥梁跨中位置。因桥上钢轨向上拱起，引起靠近路基侧的桥上钢轨产生负的转角，因此靠近桥梁的路基上的长钢轨将产生方向向下的位移；桥梁残余徐变幅值为3 mm时，钢轨最大上拱幅值为2.94 mm，桥梁残余徐变幅值为10 mm时，对应的长钢轨最大垂向变形量为9.8 mm。由图8可知：桥梁残余徐变变形幅值与桥上钢轨变形间呈现线性相关关系，且钢轨最大上拱量略小于桥梁的残余徐变变形幅值。

图7 3和10 mm残余徐变变形幅值引起的桥上钢轨变形

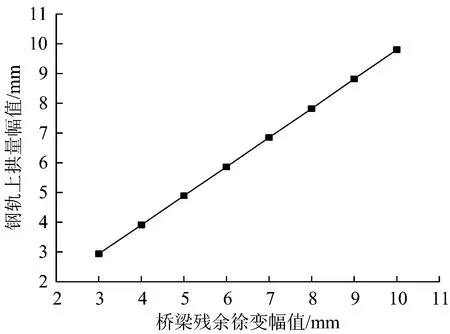
图8 不同残余徐变变形幅值引起的钢轨垂向位移幅值

3 高速铁路32 m简支梁桥残余徐变限值

目前我国高速铁路设计规范规定，铺轨后跨度小于等于50 m的无砟轨道桥面垂向残余徐变变形不应大于10 mm，现行《铁路线路修理规则》中TQI动态不平顺管理标准允许的42 m波长范围内高低不平顺峰—峰值为6 mm，两者存在矛盾，因此从动力性能角度对32 m简支梁桥残余徐变上拱限值进行进一步分析。

列车在桥梁上运行时会与桥梁间形成复杂的耦合时变体系。针对该耦合时变系统，分别建立车辆、轨道和桥梁模型，并基于轮轨接触理论将车辆模型、线路模型和桥梁模型耦合在一起。为了简化体系的分析过程，将车辆模型各部件均视为刚体，部件间均通过线性弹簧和黏滞阻尼器连接，车体、转向架均考虑沉浮、点头2个自由度，轮对仅考虑沉浮自由度，单节380BL动车车辆简化为具有10个自由度的振动系统。车辆与轨道桥梁系统垂向采用Hertz非线性接触。60 kg·m-1钢轨视为连续弹性离散点支承基础上的无限长Euler梁，并考虑钢轨的垂向振动；钢轨与轨道板间的扣件采用弹簧阻尼单元模拟；轨道板与桥梁间采用弹簧阻尼单元连接。模型长度取100 m路基+10×32 m简支梁+100 m路基，相关参数取值参见文献[16]。车辆—轨道—桥梁空间耦合动力学模型如图9所示。

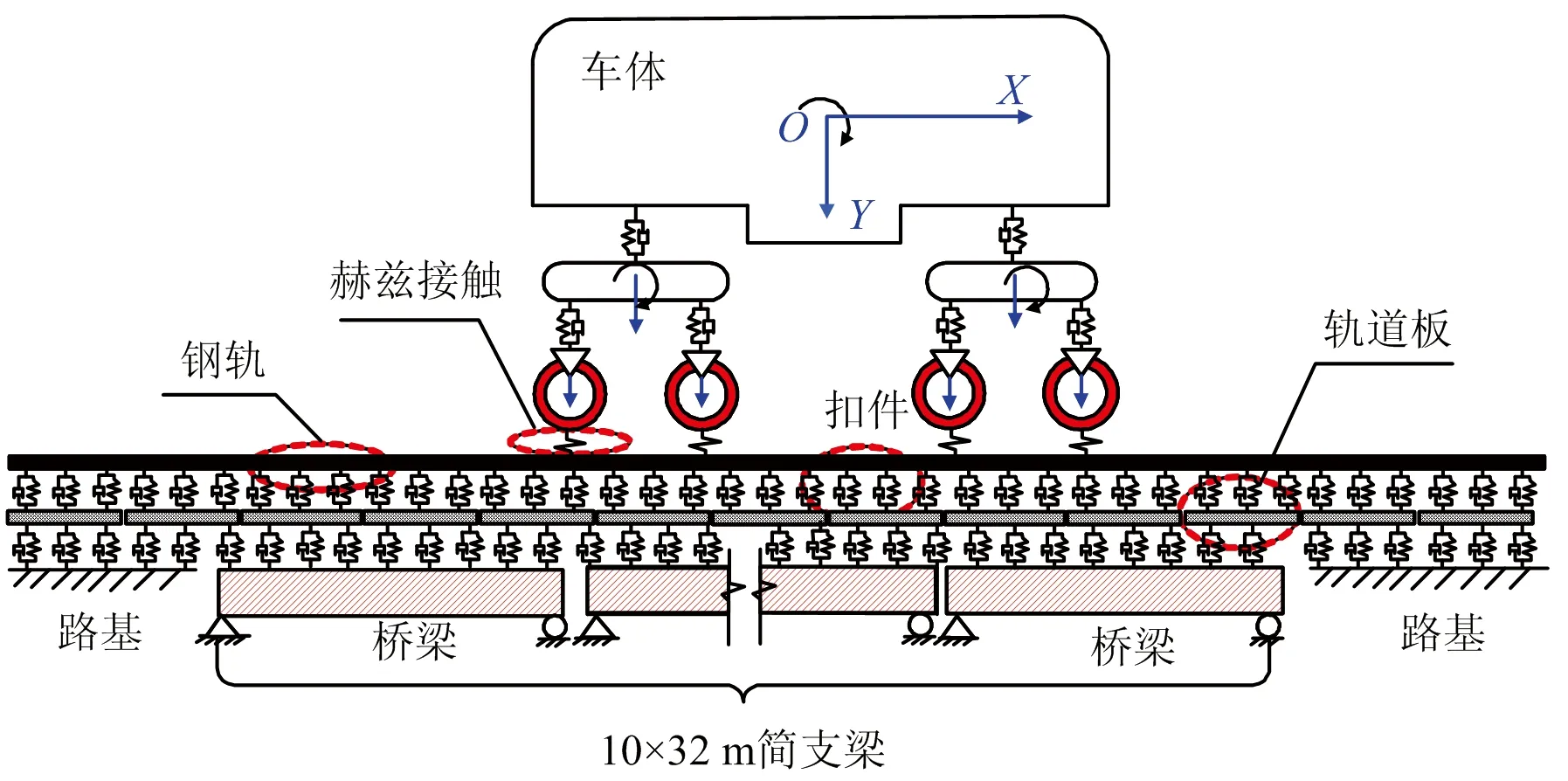
图9 车辆—轨道—桥梁耦合动力学模型

轨道不平顺为车—线—桥系统激励源，选用的随机轨道不平顺为京沪高铁路基地段实测的轨道不平顺，如图10所示。受篇幅限制，仅给出32 m简支梁桥残余变形幅值为5和7 mm时对应的钢轨轨面上拱曲线，如图11所示。将徐变上拱引起的钢轨变形作为附加不平顺，与实测的随机轨道不平顺叠加成实际输入不平顺。基于车辆—轨道—桥梁耦合动力学模型，分别计算车速280，300，320，340，360和380 km·h-1条件下车辆及桥梁的动力响应。

图10 实测的随机不平顺

图11 幅值为5和7 mm的残余徐变引起的钢轨附加变形曲线

车—轨—桥系统是一个耦合体系，桥梁的过大振动不仅使结构强度降低、线路状态发生改变，而且还会影响桥上车辆的行车安全性和平稳性。车桥系统中，车辆和桥梁是2个相对独立的子系统，两者振动特性差异较大，因此应同时对车辆、桥梁振动及行车的安全、舒适性进行评价。我国GB 5599—1985《铁道车辆动力学性能评定和试验鉴定规范》给出了行车安全性指标轮重减载率的限值为0.6。依据《高速铁路设计规范》规定，现行车体垂向加速度Ⅰ级偏差管理值为0.1g(g为重力加速度)，Ⅱ级偏差管理值为0.15g，舒适度指标合格标准为3.0。在20 Hz及以下强振频率作用下，无砟桥面的竖向振动加速度a≤5.0 m·s-2，梁端竖向转角不大于2/1 000，梁端水平折角不应大于1/1 000。本节将结合轮重减载率、车辆、桥面振动加速度、舒适度指标、梁体跨中动挠度等5个指标进行32 m简支梁桥残余徐变限值研究。

不同不平顺幅值和速度条件下桥梁的跨中挠度和加速度以及梁端加速度最大值分析结果如图12所示。由图12可知：随着行车速度的提高和徐变引起的不平顺幅值的增大，桥梁跨中的挠度、振动加速度和进出桥的桥面加速度也不断增大；当行车速度一定时，随着不平顺幅值的增大，桥梁的挠度及桥面的振动加速度峰值近似呈线性增加；当轨道不平顺幅值为7.0 mm时，行车速度360 km·h-1工况下进出桥时桥面的振动加速度幅值为5.021 m·s-2，桥面振动略微超限，但其他工况下，桥面的振动加速度仍处限值范围内；几种工况下桥梁跨中挠度最大值为1.29 mm。

图13给出了不同轨道不平顺幅值和速度条件下车体的轮重减载率、车体垂向加速度及舒适度指标。由图13可知：随着行车速度的不断提高和徐变引起的不平顺幅值的增大，行车的安全指标和舒适度指标不断增大；当桥梁残余徐变上拱幅值为10 mm，行车速度从280 km·h-1逐渐增加至380 km·h-1时，轮重减载率从0.13增大至0.24，但仍小于限值0.60，即行车的安全性指标可得到保证。当行车速度一定时，随着轨道不平顺幅值的增加，车体的垂向振动加速度近似呈线性增大；当行车速度为380 km·h-1时，残余徐变上拱幅值由3 mm增至10 mm时，车体的垂向加速度峰值由0.324 m·s-2逐渐增加至1.216 m·s-2，增加了3倍，行车的舒适度指标由1.549逐渐增至3.105，增加了1倍。可见32 m波长的长波轨道不平顺幅值是影响行车的舒适性主要因素。

图12 桥梁动力学响应

根据高速铁路设计规范，当乘坐舒适度指标大于3.0即认为舒适度指标不满足相关要求。由图13可知，当残余徐变变形幅值分别为6.0和7.0 mm时，不同行车速度下的车辆舒适度指标均小于规范要求；当残余徐变幅值为8.0 mm，在考察的车速范围内，车体的舒适度指标最大值达到3.108，超过规范要求，但其他指标仍满足限值要求；结合桥面振动加速度，考虑高速行车舒适性，建议高速铁路32 m简支梁桥铺轨后徐变上拱限值按7.0 mm控制，为避免残余徐变上拱限值对桥梁设计方案的影响，可适当通过延后铺轨时间来保证桥梁残余徐变变形小于7.0 mm。

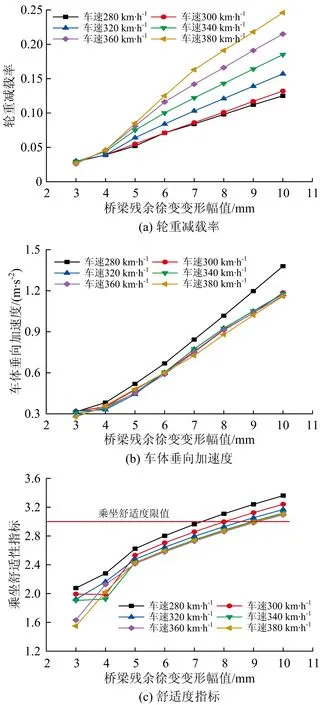
图13 不同不平顺幅值和速度条件下车辆的轮重减载率、车体垂向加速度及舒适度指标

4 结论和建议

(1)桥梁残余徐变变形是影响32 m波长周期性高低不平顺的主要因素。

(2)随着桥梁残余徐变幅值增加，长钢轨的最大上拱量呈线性趋势增大，当桥梁残余徐变变形幅值为10 mm时，钢轨的上拱变形量可达到9.8 mm。

(3)随着桥梁残余徐变变形的增加，桥梁跨中加速度、行车的安全和舒适度指标不断增大。行车速度为380 km·h-1、残余徐变上拱幅值由3 mm增加至10 mm时，车体的垂向加速度峰值由0.275 m·s-2增加至1.159 m·s-2，增加了3倍，行车的舒适度指标由1.549逐渐增加至3.105，增加了1倍。

(4)在考察的车速和桥梁残余徐变幅值下，桥梁跨中加速度、行车的安全性和车体垂向加速度可得到保证，当桥梁残余徐变幅值为8.0 mm，在考察车速范围内，进出桥时桥面的振动加速度的最大幅值为5.217 m·s-2，车体的舒适度指标最大值达到3.108，超过了规范限值。

(5)行车舒适性是控制桥梁残余徐变变形限值的主要因素，为保证高速行车的舒适性，建议高速铁路32 m简支梁桥铺轨后徐变上拱限值按7.0 mm控制，为避免对桥梁设计方案的影响，建议可适当通过延后铺轨时间保证桥梁残余徐变变形小于7.0 mm。