关于函数的两个不等式

四川省绵阳开元中学 (621000) 敬加义 黄超英

(Ⅰ)设函数F(x)=18f(x)-x2[h(x)]2，求F(x)的单调区间与极值；

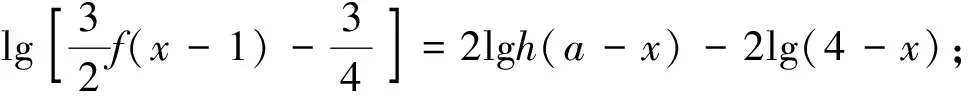
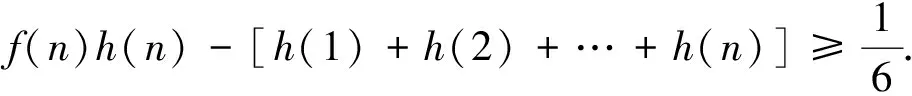
(Ⅰ)、(Ⅱ)解答略，本文运用数形结合法，通过梯形面积和定积分的意义，给出本题第(Ⅲ)问的另一种解法，并根据这种解法导出涉及区间上非负凹(凸)函数的两个不等式.

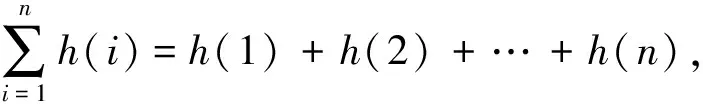
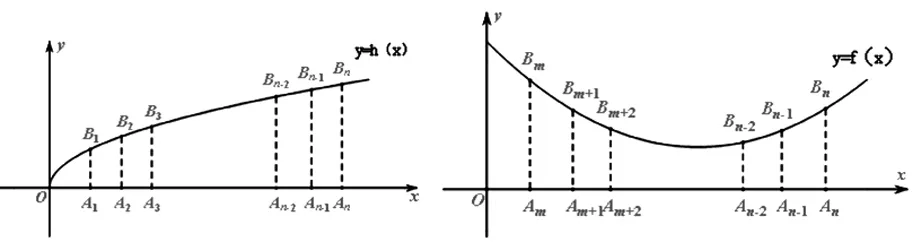
图1 图2

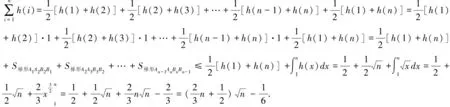
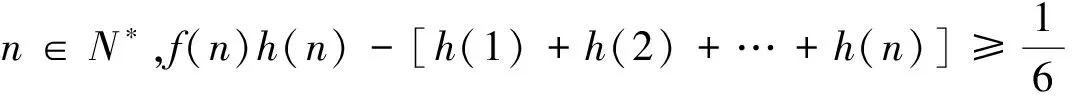
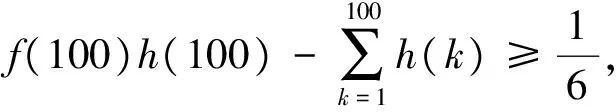
回顾上述解法，我们可得:

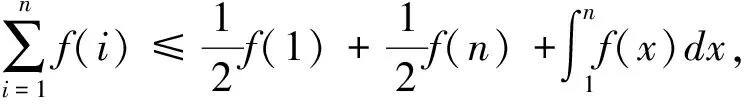
类似的，如图2，f(x)是区间[m,n]上的可积凹函数，且f(x)≥0.

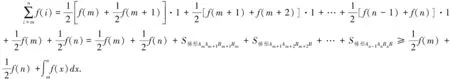
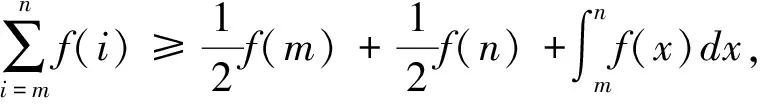
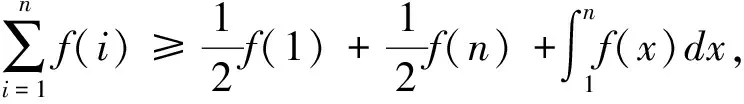
下面再举两例分别展示这两个命题的应用.

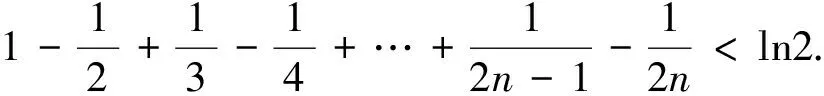
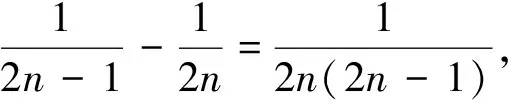
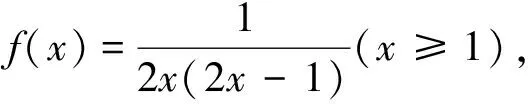
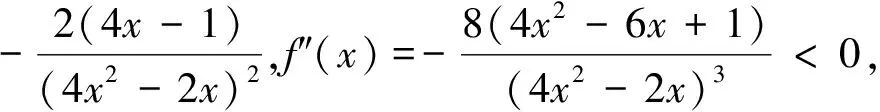
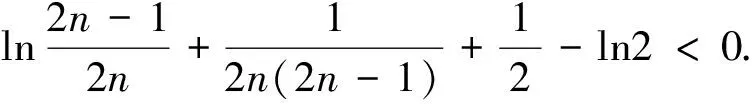
例2 (2009年高考山东卷·理·22题)等比数列{an}的前n项和为Sn，已知对任意的n∈N*，点(n,Sn)均在函数y=bx+r(b>0且b≠1,b，r均为常数)的图象上.

(Ⅰ)求r的值；

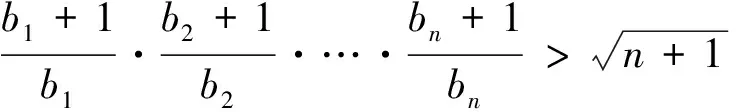
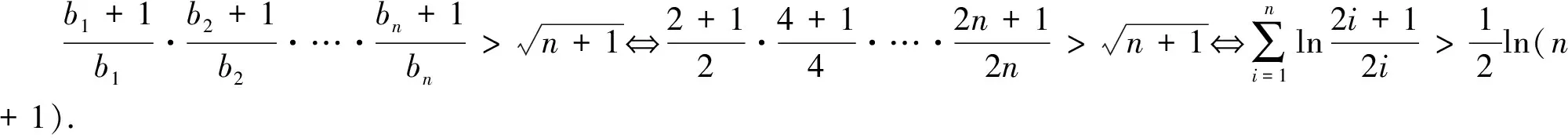
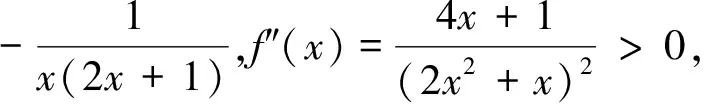
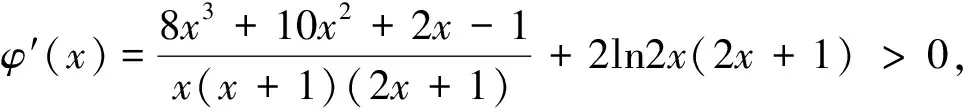
说明：1.由本文所给两个命题可得有关区间上的凹(凸)函数的不等式“更优”下界(上界)的确定方法；

2.由于“定积分与微积分基本定理”已成为“新课标”选修2—2中“导数及其应用”部分的内容，从而本文所使用解法及两个命题所给出的不等式在理解与应用上也就成为了可能,选修了该内容的学生应不陌生.