“直观想象”在高考函数问题中的渗透应用
2020-04-08浙江省永康市第一中学321300付增民
浙江省永康市第一中学 (321300) 付增民
新修订的《普通高中数学课程标准(2017年版)》中强调:突出数学素养,在数学课程逐渐展开的过程中,促进学生数学核心素养的形成和发展.直观想象是六大核心素养之一,“是发现和提出问题、分析和解决问题的重要手段[1]”,“主要表现为:建立形与数的联系,利用几何图形描述问题,借助几何直观理解问题[1]”.一说起“直观想象”,人们往往首先想到的是在几何问题中的应用,其实,“直观想象”素养在许多“数”的问题尤其是函数问题中也渗透应用的相当广泛.由于函数是高中数学的一条主线,所以与函数相关联的导数、方程及不等式的一类热问题常常在高考或各地模拟考试中以“把关定向”的角色压轴出现.这类问题不仅能考查函数知识和应用以及换元、构造、对应、图形、配凑等意识,而且依据问题的特点构造相应的函数,然后利用函数的图像直观地解决问题,因而也能有效地培养“直观想象”素养.本文以2019年高考试题或模拟题为例进行剖析,力求揭示此类试题的考查形式,探索它们的题型规律,透视其求解策略,以期抛砖引玉.
1.函数图像的判断
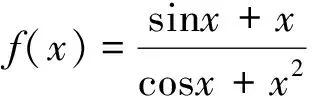


点评:函数图像的判断问题是高考的热点题型.本题先判断函数的奇偶性,得f(x)是奇函数,排除A;再注意到选项的区别,利用特殊值得到正确答案的.考查了函数的性质与图像,渗透了逻辑推理、直观想象和数学运算素养.
2.利用图像进行命题判断

A.①④B.②③C.①②③D.①③④
解析:根据题意,作出函数图像.

由图可知2π∈[x1,x2)由题意可得


点评:本题首先作出函数的图像,然后结合图像的直观性,并通过分析、运算分别对命题逐一作出判断的.
3.函数方程中关系式的求解值问题

A.-1B.0C.1D.2
解析:作出函数f(x)=

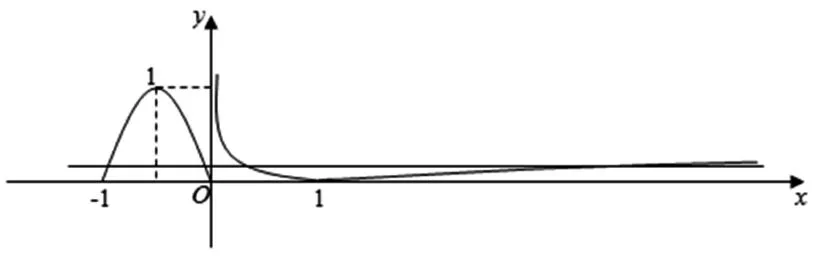
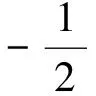
点评:本题首先作出函数的图像,然后利用图像所呈现的函数的性质,整体求值,最后代入求解的.很好地考查了整体处理的意识和直观想象、逻辑推理等核心素养的运用.
4.函数方程中参数范围的确定





5.函数不等式中参数范围的确定

解析:∵x∈(0,1]时,f(x)=x(x-1),f(x+1)=2f(x),∴f(x)=2f(x-1),即f(x)右移1个单位,图像变为原来的2倍.


点评:本题为选择压轴题,结合题意画出示意图,借助图像直观,分析出临界点位置,并通过精准运算求解的.利用函数的图像直观使问题的解决明朗化,是培养和形成直观想象数学核心素养的良好途径.
新一轮的课程改革已经进入了关键时期,在教育教学中越来越强调要培养学生的数学核心素养和学习能力.近年来,高考制度的改革给高中数学复习备考也带来了深刻的变革,在复习中教师越来越注重学习方法、解题方法的传授,而不仅仅只是向学生传授基础的学科知识.数学是学生学习生涯中促进其能力发展、思维提高以及认知水平提高的一个基础性学科.但是由于高中数学知识的复杂性、抽象性使很多学生在学习过程中望而生畏.教师在数学解题教学中教学方式以及教学理念若运用不当,就会使得学生的学习效率低下,表面上看每天都沉浸在高压的学习下,但是并没有什么太大的效果.因此,教师必须要转变教学理念和教学方式,引导学生对不同类型题目的特征进行总结和归纳,掌握不同的解题方法,让学生在做题实践中体会数学的魅力.直观想象作为六大数学核心素养之一,恰当而合理的运用,确实会给一些数学问题的解决带来事半功倍的效果.有教师曾感慨道,导数的学习给函数的研究插上了翅膀,而从上述问题的解决可以进一步看到,直观想象素养在求解函数热点问题特别是一些压轴小题的有效运用,相当于给函数问题的研究和求解又插上了另一只翅膀,展开双翅,这样对于诸多函数问题的解决也许就会飞的更高、更远……
