注重解题过程分析 揭示数学探究途径
——以一道不等式题的探究为例
2020-04-08重庆市潼南中学402660彭思锐
重庆市潼南中学 (402660) 彭思锐
数学探究是高中数学课程标准中要求的内容之一,在中学数学教学中如何进行数学探究,是每一位数学教师都值得思考的问题,本文通过对一道不等式题的探究过程的揭示,对数学探究的途径作一探讨.

(数学通讯2018第7期问题征解364题)
不等式(1)结构对称,证明方法多样[1],对不等式的探究除证明方法的多样外,还需关注与不等式(1)相关的一些问题.为此利用柯西不等式和基本不等式给出不等式(1)的一种简捷的证明,并通过对证明过程的分析,来探究与不等式(1)结构类似的不等式和(1)的推广.
1.不等式(1)的证明

记不等式(1)的左端为M,整理得

分析:从证明过程可以看出,利用柯西不等式变形整理后的(2)式的左端的分子,分母分别为不等式(1)的左端的分子分母相应的项的和构成,显然,只要(2)式右端的分子,分母的结构不变,其证明过程也完全相同,因此,如果将不等式(1)的分子或分母的项进行适当的重组,扩充,或变式,将会得到许多与(1)结构类似的不等式.
2.不等式(1)的类似不等式
2.1 交换分子或分母的顺序
若注意到(2)式右端的分子与分母分别是(1)式左端各分式的分子与分母的和,因此,只要(1)式左端分子,分母的和不变,其结论都是成立的,因此,将(1)式各分子或分母的顺序交换可得新的不等式.

2.2 若将(1)各分式的分母的项扩充.相应的不等式(2)的分母的和发生变化,但其证明思路不变,从而可得结构与(1)类似的不等式.
不等式2 已知正数ai(i=1,2,…,n),2≤n∈N+,满足:a1a2…an=1,求证:
不等式3 已知正数ai(i=1,2,…,n),2≤n∈N+,满足:a1a2…an=1,求证:


2.3 若将(1)式左端分母中的根式里面的项扩充,可得结构与(1)类似的不等式.


2.4 若将(1)式左端分母中的根式里面的项添加系数,可得结构与(1)类似的不等式.


2.5 若将(1)式左端分子叠加,可得结构与(1)类似的不等式.



不等式13 已知正数ai(i=1,2,…,n),2≤n∈N+,满足:a1a2…an=1,λ,μ>0,求证:
显然,不等式(1)的左端的分子,分母的项的变式以及相应项的系数的搭配不止上述几种,因此还可以得到许多新的不等式.
3.不等式(1)的推广
与不等式(1)的证明类似,可以将不等式(1)左端分子的次数进行推广,有:


记不等式(3)的左端为N,整理得

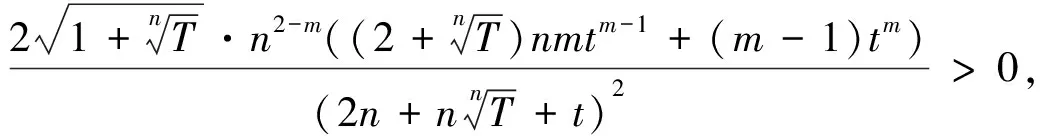
特别地,当T=1时有:

同不等式(1)的讨论一样,对不等式(3)和(4)的进行变式,可得到许多结构与(3)和(4)类似的不等式,在此不再赘述,有兴趣的读者不妨一试.
