以旋转为例谈图形变换专题复习

福建省厦门市同安区厦门实验中学(361116) 刘云啟

《义务教育数学课程标准(2011 版)》对旋转的要求为:会说出旋转的定义和它的基本性质,理解旋转前后对应点到旋转中心的距离相等,对应点与旋转中心连线所成的角彼此相等的性质；能按要求作出简单平面图形旋转后的图形,理解中心对称图形和旋转对称图形的转化关系．结合近几年全国各地市的中考题,不难发现,在选择题、填空题和解答题中都会考查到旋转．而在复习过程中,学生遇到考查旋转综合题时,借助常规方法往往难以解决问题．浅层原因在于通过旋转构造辅助线是学生学习的一大难点,深层原因在于学生尚未有效掌握旋转的本质．

数学教育家傅种孙先生曾言:“几何之务不在知其然,而在知其所以然；不在知其所以然,而在知何由以知其所以然”．这为数学的学习标明了三个递进的境界:一是知其然,二是知其所以然,三是知何由以知其所以然．笔者认为,紧扣中考考试大纲,以基础知识、基本技能、基本能力和基本思想构成的“四基”为复习路径,不仅能较好地夯实知识点,掌握相应的数学思想和方法,而且可以作为中考数学专题复习中比较有效的方式,这与傅种孙先生的观点不谋而合．本文以旋转这一知识点为例,谈谈如何在图形变换专题复习中实践以上复习方式．

1 重视概念,夯实基础知识

华罗庚先生指出:“复杂的问题要善于‘退’,‘退’到最原始而不失去重要性的地方,是学好数学的一个诀窍”．夸美纽斯在《大教学论》中提到:“在尽可能的范围内,一切事物都应尽力地放在感官的跟前．更好地理解旋转,莫过于从最原始的地方出发——动手操作．

例1给定一张钝角ΔABC的纸片,以A为圆心,把ΔABC绕点A逆时针旋转180°．

(1)想一想纸片绕点A旋转的过程；

(2)请用给定的纸片在图1中转一转；

(3)请画出点C的对应点在BC延长线上时的对应图形,点B的对应点在BC延长线上时的对应图形,点B的对应点在BA延长线上时的对应图形以及画出一个把ΔABC绕点A逆时针旋转任意角度所得到的图形；

(4)将这四个新得到图形分别和原图形进行观察比较,你发现了什么?

图1

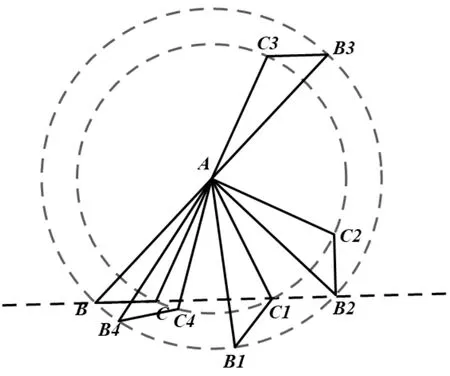
图2

评注分设4 个问题的目的在于借助圆,学生能够直接感知图形旋转路径,有利于培养学生空间想象能力；将旋转附着在圆上,学生更易理解旋转的本质特征,有利于深化学生化归与转化思想；通过不同旋转位置新旧图形(如图2)的比较、探究,总结出旋转的共性,有利于学生掌握从特殊到一般的数学思想方法．

虽然旋转的概念比较容易理解,但在复习基础知识时,不应一味追求以做题巩固知识点,而应追根溯源,弄清楚旋转概念的内涵与外延．知其然,也要知其所以然,为提升基本技能做铺垫．

例1可以作为学案的内容,学生课前完成．专题复习课时间有限,把一部分内容移植到课前完成,为课堂教学赢得时间和空间．通过课堂进一步讲解,学生经历两次思考对比后,对旋转的理解会更为透彻．在教学时还应注意,旋转点除了在几何图形的顶点(边上的特殊点)上,还可以在图形外,边上(排除顶点),图形内部．教师应要求学生自主解决其它三种情况,这有助于巩固学生分类讨论意识,加强学生识图作图能力,渗透转化与化归的数学思想．

例2(2017年南通中考数学卷,15)如图3,将ΔAOB绕点O按逆时针方向旋转45°后得到ΔCOD．若∠AOB=15°,则∠AOD=_____度．

变式1(2018年衡阳中考数学卷,13) 如图4,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按顺时针方向旋转而得到的,则旋转的角度为______．

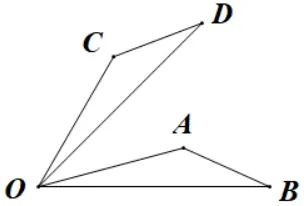
图3

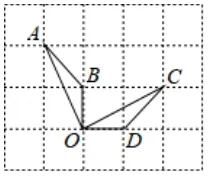
图4

评注虽然例2 和变式1 可以直接利用旋转的性质很快得出答案,但应引导学生从源头上去认识题目,将圆作为旋转的知识生长点,以基础题的形式呈现,学生可以更清楚地理解旋转．只有回归本质,建立起旋转知识点的强大根系,学生才能够适应在基本技能和基本能力方面的考查．

2 严密推理,巩固基本技能

中考除了对旋转知识点单一技能考查外,更倾向于结合其它知识点,以局部知识网络的形式检测学生的数学水平．

例3(2017年天津中考数学卷,9) 如图5,将ΔABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB的延长线上,连接AD．下列结论一定正确的是( ).

图5

A.∠ABD=∠EB.∠CBE=∠C

C.AD//BCD.AD=BC

评注例3 考查了旋转的性质、平行线的判定以及等边三角形的判定．在熟练掌握基础知识的前提下,建立知识点间的联系进行技能叠加,达到解决题目的目的．学生形成解决旋转的基本技能,有助于实现同类型题目的多题一解．我们给出例3 的变式2．

变式2(2018年山西中考数学卷,8) 如图6,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到ΔA′B′C,此时点A′恰好在AB边上,则点B′与点B之间的距离为( ).

图6

A.12 B.6 C.6D.6

评注题目条件发生了改变,但解题的核心依然是旋转的性质．从形式、内容以及方法上可以发现变式2 与例3 高度相似．熟练掌握多题一解的能力,还需要抽取不同题目的共性,牢牢抓住解题的本源．我们给出例3 的变式3．

变式3(2018年江西中考数学卷,10)如图7,在矩形ABCD中,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点E的对应点落在CD上,且DE=EF,则AB的长为_____．

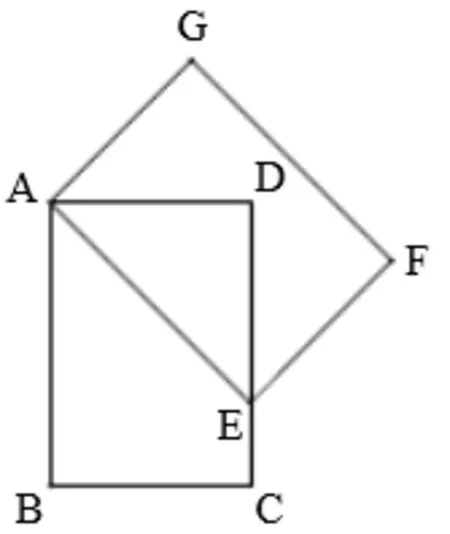
图7

评注虽然题目条件不一样,图形有别,涉及的考点又有所不同,但都考查了旋转的性质．

有效挖掘题目条件并加以运用,解决上述类型的题目并不难．而学生遇到比较复杂的旋转问题时,即便结合已知条件分析图形,也难以下手．这就需要理解旋转本身是一个动态的过程,应当从运动的视角去思考图形变换的内在联系,认识图形大小、图形位置变与不变的本质特征．

例4(2019年厦门数学质量检测试卷,23) 在四边形ABCD中,AB//CD,∠ABC=60°,AB=BC=4,CD=3.

(1)如图8,求ΔBCD的面积；

(2)如图9,M是CD边上一点,将线段BM绕点B 逆时针旋转60°,可得线段BN,过点N作NQ ⊥BC,垂足为Q,设NQ=n,BQ=m,求n关于m的函数解析式．(自变量m的取值范围只需直接写出)

图8

图9

评注结合旋转角度,利用旋转过程中线段长度的不变性,联想到三角形全等的条件,进而构造辅助线．突破这个障碍,求解问题就会比较容易．

通过这四道试题的展示,可以清晰地发现例1 的探究是十分有必要的．如果对例1 深入理解,就能够掌握圆是图形旋转知识点生长延伸的最好土壤这一共性．学生通过不同题目的比较分析,建构知识点之间的关系,形成局部的知识网络．由单一技能向多技能叠加的转变,从而掌握旋转的基本技能,也为进一步提升基本能力打好基础．熟练进行技能叠加的前提是对每一个知识点追根溯源的执着,关键是不断通过题目进行风雨历练,精做精析精思,才能迎来雨后的彩虹．

3 注重反思,提升基本能力和思想

由于图形变换能较好地考查学生直观想象、猜想推理,分析解决问题的能力,而旋转是最复杂的一种图形全等变换．各省市命制质检题、中考试题时会将旋转以压轴题的形式呈现．

例5(2018年厦门中考数学卷) 已知RtΔABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF,分别与直线AB交于点M,N．

(1)当扇形CEF绕点C在ACB的内部旋转时,如图10,请探究线段MN,AM,BN之间的等量关系,并说明理由；

(2)当扇形CEF绕点C旋转至图11 的位置时,第(1)题的关系式是否仍然成立?若成立,请证明；若不成立,请说明理由．

图10

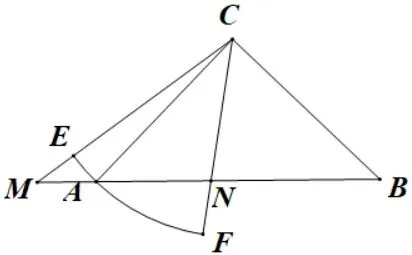
图11

评注结合已知条件进行局部推导,较多的学生是可以做到的,但鲜有学生能够做到完整推导,足以反映上述试题不再是单纯的技能叠加,说明本题重在考查学生的数学能力,区分学生的层次．

解析几何题最常用的方式是直观想象与逻辑推理．直观想象以抽离基本图形与运动变化为主,逻辑推理最常用的就是综合-分析法．不妨从这两个思路引导学生分析,培养学生解决难题能力的同时,还应抓住学生的思维困惑点．例如,为什么AM,BN,MN之间不存在和、差及不等关系?可以通过直尺测量的方法进行初步验证猜想错误．为什么将三边放在一起思考?是三边同在一条直线上还是构成一个三角形?需要关注基本图形(等腰直角三角形)和特殊条件45°角,这是朝旋转思考的提示点,从而联想到“作旋转证全等”．在建立题目条件之间关系时,思维路径的引领上应当更有方向性,逻辑性上有理有据．

变式4(2018年龙岩中考数学卷,10)如图12,∠ACB=90°,AC=BC,∠DCE=45°,如果AD=3,BE=4,则BC的长是( ).

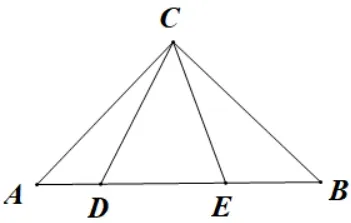
图12

A.5 B.5C.6D.7

评注共性寓于事物的个性之中,一般性寓于特殊性之中．对例5 总结反思的基础上解决变式4,找到题目的共性不再那么复杂．利用边角的特殊性借助旋转进行边角转化,无形中就将数学思想方法内化到思维路径的推导中,有效地把知识点、数学思想方法紧密联系起来．学生不仅能够内生归纳总结一类题的意识,而且还能培养自身宏观把握的能力,从而学生既能“林中观其树的结构”,又能“空中俯瞰林的轮廓”．

稳固的基本技能要求学生能够联系多个知识点,形成局部知识网络,而掌握好基本能力和思想则要求学生能够进行技能叠加的嵌合,把局部网络编织成一个更大的知识网络．现在我们可以感知到学生难以解决旋转压轴题的原因正是缺乏技能叠加之间的嵌合．如何嵌合才能使学生在这一块能得高分?波利亚在《怎样解题》中写道:“怎样解题的最后阶段是回顾”,他指出:“通过回顾完整的答案,重新斟酌、审查结果及导致结果的途径,他们能够巩固知识,并培养他们的解题能力．没有任何一个题目彻底完成了的,总还会有些事情可以做”．因此,解题后的反思总结是沉淀学生数学能力的重要时机．启发学生思考为什么可以用旋转解题,引导学生如何利用图形旋转不变的数量关系和图形结构,以不变应万变．总结用旋转解题的优势在哪里．解题过程中运用了哪些知识点?知识点之间是如何串联在一起的?如何通过知识点体现数学思想方法?同时,针对探究线段数量关系的题目,引导学生总结一些常见的结论类型,增加解题灵感,优化思维路径．

学生数学能力的提升非一朝一夕之事,需要时间的积累沉淀．无论是新授课、一轮复习还是专题复习,应该引导学生不忘初心,从最根本的地方入手,一步一个脚印,学懂弄通做实．在遇到较难问题时,才能够如泉水般涌现出解题思路．

4 感悟

旋转复习是“由点成面”的过程,即在基础知识上理清吃透知识点；在基本技能上用题目“包抄”知识点,强化局部知识网络,形成解决知识点的内驱力；在基本能力和基本思想上,数学思想方法是主线,无论是猜想验证所凸显的特殊到一般的思想,还是边角转化所渗透的化归与转化思想,可以发现思维路径中数学思想贯穿始终．通过“四基”复习路径,不仅复习了旋转知识,还串联了其它知识点,可以使不同层次的学生得到提高,能够有效因材施教,提升中考数学复习的质量．此外,“四基”复习路径有助于学生更好地实现数学能力和数学思想的形成,发展学生的数学核心素养,从而学生能够从数学的视角分析问题,以数学的思维思考问题,用数学的方法解决问题．