考虑设备可靠性与能耗的平行机调度
2020-04-08许显杨
许显杨, 陈 璐
(上海交通大学 工业工程与管理系,上海 200240)
制造业是社会发展的重要支柱,而制造业的发展带来了巨大的能源消耗.2016年我国制造业能源消耗量达 247 792.83 万吨标准煤,占我国能源消费总量的56.9%[1].在保证生产能力的同时降低企业能耗,是制造企业构建核心竞争力的关键,而通过生产调度手段降低生产系统能耗已成为近年来的研究热点[2].如:Liu等[3]的研究结果表明延长1.3%的完成时间可节约22.5%的能耗;Yan等[4]列举的包含7个加工任务的生产案例中,通过调度手段节约了1.88 kW·h 的电能,且节省的电能会随着加工任务数量的增加而成比例递增.以较低的优化成本、较短的更新周期节约可观的加工能耗方面,调度手段具有巨大的潜力.
从需求端降低能耗的调度问题可以分为考虑非加工能耗与考虑加工能耗两类[2].针对降低非加工能耗问题的研究大多采用开关机(On-Off)机制,即关闭长时间不作业的设备以降低其空转能耗.Che等[5]考虑开关机造成的额外能耗与时间浪费,并以此确定最小可关机时间间隔,建立了同时最小化延迟和能耗的多目标优化模型.王君[6]考虑开机能耗与关机能耗,建立了以任务分配、任务起始加工时间、设备关机节点为决策变量的调度模型.Yildirim等[7]考虑启动能耗,建立了以最小化完成时间和能耗为目标的混合整数模型.Cheng等[8]则仅考虑开机能耗,建立了分时电价下考虑开关机机制的调度模型.
从加工能耗角度建立模型多采用加工速度可变(Speed-Scaling)机制,即考虑不同加工速度对系统能耗及生产能力的影响.Fang等[9]针对流水线车间建立优化模型,除调度序列外将加工速度也作为决策变量之一.吴秀丽等[10]则研究了柔性作业车间内的多转速策略,以最小化加工完成时间与总能耗.加工速度可变机制的内涵可以进行拓展,如考虑刀具规格、切削速度、进给速率、切削深度等[11]在内的切削参数,以及不同设备类型对于能耗及加工能力的影响.Wang等[12]考虑不同切削条件对能耗及加工能力的影响,利用两阶段启发式算法降低了平行机车间的加工能耗.He等[13]考虑设备类型对能耗的影响,将设备选择与调度序列作为决策变量建立了数学模型.李聪波与何彦等[14-15]研究柔性作业车间,在调度模型中考虑工艺路线对于能耗的影响,提出了节能调度方法.
Yan等[16]的研究表明随着可靠性的下降,加工能耗随之升高.Dahmus等[17]对实际数据的分析结果表明,设备老化将带来更高的加工能耗.然而,目前考虑能耗的调度研究中多将设备健康状态视为稳定的且在调度过程中不发生改变,这与实际加工的情况偏差较大.Nezami等[18]提出的三目标优化问题,利用开关机机制同时最小化能耗、完成时间与最大化可靠性,但模型中将能耗与可靠性视为完全无关的变量.Yildirim等[19]提出设备可靠性的下降导致加工时间延长,但忽略了可靠性对加工能耗的影响.
本文研究平行机调度问题,考虑可靠性对加工能耗的影响,建立了以最小化能耗成本与延迟成本加权和为优化目标的数学规划模型,设计开发了蚁群算法对问题进行求解,最后利用算例实验证明了算法的有效性及具有的较高效率.
1 能耗与设备可靠性关系的定义
可靠性是指产品在规定条件下和规定时间内完成规定功能的能力[20],用可靠度函数R(t)表示,定义为系统或部件在时间t内正常工作的概率.本文采用指数型可靠度函数对设备的可靠性进行建模,其在系统或部件的可靠性研究领域是最常用的分布函数之一[20].可靠度函数
Rk(Lk)=exp(-λLk),t≥0
(1)
式中:λ为故障率;Lk为设备k经过上一次维护变为全新状态后的累积加工时间.
在设备的一个维护周期内,随着设备使用时间的累积,其可靠性rk随之逐渐下降(见图1(a)),而任务i的加工功率Ei随之逐渐增加[16](见图1(b)).

图1 设备加工功率与可靠性的关系
基于图1中设备加工功率与可靠性的定性映射关系,本文定义设备加工任务i的实际加工功率与设备可靠性rk的定量关系为
(2)

2 模型建立
在加工车间内有平行机集合M,且各设备的初始状态是不同的.需要对集合N中的任务进行加工,目标设定为最小化能耗成本与延迟成本.模型假设:① 所有的任务在0时刻即可以开始加工;② 每台设备在同一时刻仅能加工1个任务;③ 加工过程不允许被打断;④ 任务不允许使用多台设备进行加工;⑤ 在单个任务的加工过程中,设备的可靠性不发生变化.
模型中的基本符号:N′为包含虚拟任务“0”的任务序号集合;pi为任务i的加工时间;di为任务i的交付期;L0k为设备k在调度开始前的累计加工时间;B为一个极大的正数;γ为单位延迟时间的成本系数;ε为单位能耗的成本系数;δ为能耗成本的权重系数.
模型的决策变量xijk为0/1变量,如果在设备k上任务j紧随任务i后进行加工,则取1,否则取0.
辅助决策变量:Ci为任务i的加工完成时间;Lik为设备k在任务i加工开始前的累计时间;rik为设备k在任务i开始加工前的可靠性;ei为任务i的实际加工功率.
由此建立数学模型如下:
(3)

(4)
(5)
(6)
(7)
(8)
∀i∈N,k∈M
Cj-Ci+B(1-xijk)≥pj
(9)
∀j∈N,i∈N′,i≠j,k∈M
Ljk-Lik+B(1-xijk)≥pi
(10)
∀j∈N,i∈N′,i≠j,k∈M
(11)
∀j∈N,k∈M
(12)
∀j∈N,k∈M
(13)
∀i∈N,j∈N,k∈M
目标函数即式(3)包含两部分:第一部分为能耗成本,由单位能耗成本系数与总能耗的乘积来表示;第二部分为延迟成本,由单位延迟时间成本系数与总延迟时间乘积表示.式(4)与(5)保证一台设备的虚拟任务“0”前后至多只能有1个任务进行加工.式(6)与(7)保证任务仅能在1台设备上进行加工.式(8)保证每个任务仅能有1个前序任务和1个后序任务.式(9)描述了任务与其前序任务完成时间的关系,式(10)表示了任务与前序任务设备累计加工时间的关系.式(11)与(12)分别为可靠性及能耗的计算关系.式(13)定义了模型中各个变量的取值范围.
以最小化总延迟成本为优化目标的平行机调度问题是NP-Hard问题[21],而相较于传统的平行机调度问题,本文在平行机调度问题中考虑了设备可靠性对能耗的影响,引入了计算可靠性的非线性约束(式(11)),更增加了求解难度.如当设备数量为3,任务数量为10时,模型共有462个变量,757个约束,Lingo求解器在24 h内无法得到最优解.因此,为了求解大规模问题,本文开发了更为高效的蚁群算法.
3 算法设计
为了解决提出的调度问题,本文设计开发了一个蚁群算法(ACO).首先,基于ATC(拖期成本)规则提出了新的启发式规则用于生成初始解,以确定蚁群算法的参数及构造流程;然后,通过设备选择,任务选择,任务分配3个过程构造调度解,将任务分配到设备上,完成调度序列的构造,并提出了创新的蚁群搜索启发因子,定义了蚁群的搜索过程;最后,引入了局部搜索算法提升解的质量.具体的算法流程如下.
3.1 初始解生成
本文提出了新的启发式规则用于生成初始解,用于确定蚁群搜索流程及算法参数.
步骤1设U为所有未加工任务的集合,tk是设备k上所有已分配任务的加工完成时间.初始时,U=N,tk=0,k∈M.


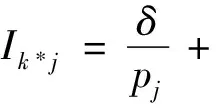
(14)
步骤4将任务j*分配到设备k*的加工序列的下一个位置.更新tk*=tk*+pj*,令U=U/j*.
步骤5重复步骤2~4,直到所有任务分配完成,即U=∅.
步骤6对每一台设备的加工序列进行相邻任务交换操作,提升解的质量.

3.2 蚁群算法调度序列的构造
在传统的以最小化延迟成本为目标函数的平行机调度问题中,多将解的构造分为两个阶段:分配与排序[22].本文的模型需要同时最小化能耗成本与延迟成本,因此提出了一个三阶段的构造方式,即设备选择、任务选择与任务分配,得到|M|维向量表征得到的调度序列.
3.2.1设备选择 构造调度序列首先需要选择一个设备,选择方式由初始解能耗成本与延迟成本的关系确定.首先生成一个符合[0,1]均匀分布的随机数qa,qa0是用户定义的表征探索偏好的常数,且 0≤qa0≤1.当qa≤qa0时,选择所有设备中累积加工时间最短的设备,或是选择最先可用的设备;否则,基于概率分布Pk随机选择设备k.
(15)

(16)
(17)
(18)
如果初始解能耗成本高于延迟成本,则依据式(15)和(16),即根据设备累计加工时间选择设备;反之,则依据式(17)和(18),即基于设备最早可用时间选择设备.
3.2.2任务选择 设备选择完成后,蚁群需要基于所选设备k*选择一个任务.在这个阶段,选择任务基于信息素强度τk*j与启发因子ηk*j,重要程度分别为α与β.其中,启发因子ηk*j=Ik*j.任务选择的步骤具体如下:生成符合[0,1]均匀分布的随机数qs,当qs≤qs0时,选择使得(τk*j)α(σηk*j)β最大化的任务j*,其中σ为比例系数;否则,基于概率分布Pk*j选择任务j.选择过程为
(19)
(20)
3.2.3任务分配 考虑到各个设备的可靠性不同,带来的额外能耗有所差别,因此在第3阶段根据下式为第2阶段中选择的任务j*分配设备,采用贪心策略选择使目标函数值最小的设备.
k**=arg min[δεEj*(e-λ(L0k+tk))+
(1-δ)γmax{tk+pj-dj,0}]
(21)
基于这样的重选过程选择了任务与设备,代表任务分配到设备进行加工.
3.3 局部搜索
当所有任务均已分配完成时,一个完整的调度序列已构造完成.为进一步提升解的质量,采用如下两个局部搜索算法规则对现有调度序列进行改进.
规则1同一设备上的任务交换.随机选择设备k,选择在设备k上加工的任务j1与j2,交换j1与j2.
规则2任务在不同设备之间的交换.选择目标函数值最高的设备和目标函数值最低的设备,在设备k1加工的任务中选择任务j1,在设备k2加工的任务中选择任务j2,交换j1与j2.
3.4 信息素更新
在所有蚂蚁找到可行解后,需要对信息素进行更新,以便于对后续循环中的蚂蚁进行指导,获得更优的目标函数值.当一次循环内所有蚂蚁完成搜索后,分以下3种情况进行信息素更新:① 若在当前的全局最优调度中任务j在设备k上进行加工,则增加信息素τkj强度;② 若在本次循环内的最优调度中任务j在设备k上进行加工,则增加信息素τkj强度,但增加的信息素少于全局最优调度;③ 其余路径信息素τkj强度不增加.
τkj(t+1)=(1-ρ)τkj(t)+ρΔτkj,best
(22)
(23)
式中:Sbest及Obest表示全局最优调度方案及其目标函数值;Slbest及Olbest表示本次搜索最优调度方案及其目标函数值.
3.5 ACO算法流程
设当前蚂蚁搜索得到的调度方案为Sants,目标函数值为Oants,综合以上各阶段的流程,本文提出的ACO算法具体步骤如下.
步骤1算法参数α、β、qa0、qs0、ρ、ITER、ANTS初始化,令iter=1.
步骤2令ants=1,U=N,tk=0,k∈M.
步骤3设备选择.根据初始解中延迟成本与能耗成本的比例,依据式(15)~(18)选取设备k*.
步骤4任务选择.基于信息素强度τk*j与启发因子ηk*j,根据式(19)和(20)选取任务j*.
步骤5任务分配.贪心策略,选择使目标函数值最小的设备k**加工j*,如式(21).
步骤6令U=U/j*,tk**=tk**+pj*,如果U=∅,则转入步骤7;否则,转入步骤 3.
步骤7执行局部搜索算法提升解的质量.
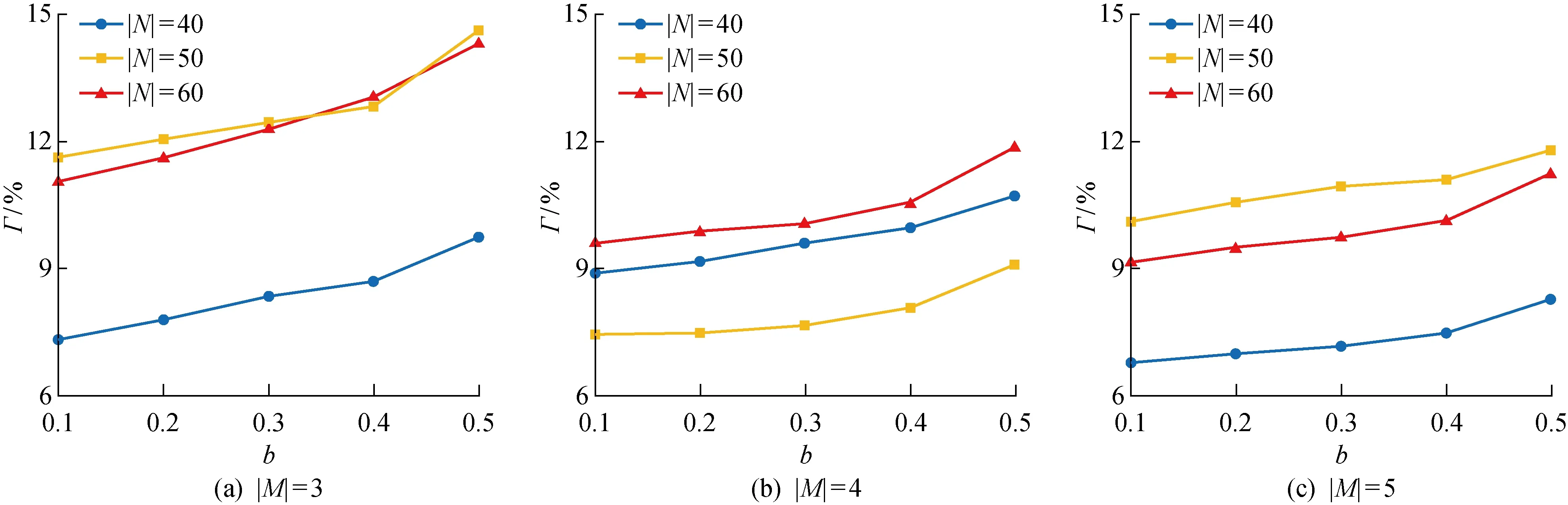
步骤8若Oants 步骤9令ants=ants+1,如果ants>ANTS,那么转入步骤 10;否则,令U=N,tk=0,k∈M,转入步骤 3. 步骤10若Olbest 步骤11令iter=iter+1,如果iter>ITER,那么转入步骤 12;否则,转入步骤 2. 步骤12算法终止. 为了验证ACO算法的性能,本节应用1组小规模算例和3组大规模算例对算法进行了测试.采用Python 2.7.13 测试算法,所有的计算实验均在配置为Intel(R)Core(TM)i5-7200U(2.50 GHz)处理器、8 GB内存的个人电脑上进行. 表1 算法参数水平值设置 为求得小规模问题的最优解,采用Lingo17.0对数学模型进行求解,如果1 h内无法算出最优解,则终止求解器并以当前求得的可行解作为最终解.取T=0.5,R=0.8生成各任务交付期.设备、任务数量,以及设备初始累积加工时间L0k设置如表2所示.共设置12种不同组合的小规模算例,每种组合均以参数生成规则随机生成10组算例,分别利用Lingo与ACO算法求得最优解,并取结果平均值进行比较.以ACO算法与Lingo求解器的偏差程度作为评价指标,即 小规模算例的实验结果如表3所示,其中ti(i=ACO,Lingo)为采用i时的求解时间.结果表明:当Lingo可以在规定时间内求得最优解时,ACO算法求得的最优解与Lingo求得的最优解完全一致.而随着任务数量增加,Lingo在有限时间内无法获得全局最优解,此时ACO算法得到的最优解优于Lingo在规定时间内得到的最优解.同时,在求解时间上,ACO算法明显优于Lingo,在求解效率上更具优势. 表2 小规模算例参数设置 表3 小规模算例实验结果 当可靠性函数中参数λ=0.000 3,可靠性阈值为0.4时,计算可得设备的一个维修周期内的可用寿命为 3 054 h.为了定义各台设备在初始状态时可靠性的偏差程度,引入系数b表征设备初始累计使用时间L0k的偏差程度.取所有设备L0k的中位数为 1 500 h,初始可靠性最低及最高的设备L0k分别取 1 500(1-b)和 1 500(1+b),其余设备分别取分位数.b值越大,则各设备初始可靠性的偏差程度越大.考虑到ACO算法的随机性,在进行算法求解效率分析、调度方法比较与敏感性分析时,每种参数组合的实验均按条件生成10组随机算例,并取10组算例计算结果的平均值进行对比和分析. 4.3.1算法表现分析 问题参数设置与小规模算例相同,取b=0.5,验证蚁群算法在解决大规模问题时的效率,同时与3.1节中提出的启发式规则得到的初始解Oinit进行比较,验证ACO算法的求解优势.求解结果如表4所示,表中数据为10个随机算例计算时间的均值.从表中的结果可以看出,ACO算法在求解大规模问题时效率较高,可以在较短的时间内求得满意解,且解的质量较之于初始解有明显改善. 表4 ACO算法的效率与表现 4.3.2考虑可靠性的调度方法与不考虑可靠性的调度方法比较 为了验证本文所提出的调度方法对于降低生产成本的有效性,随机生成9组算例,分别计算考虑设备可靠性与不考虑设备可靠性时的目标函数值.b分别取0.1、0.3、0.5,代表了设备初始可靠性不同偏差程度的3种加工场景,计算结果如图2所示.图中:D′=(OCon-ONon)/ONon,OCon为利用本文调度方法得到的目标函数值,ONon为不考虑设备可靠性时的目标函数值.本文提出的ACO算法可以用于不考虑设备可靠性时的平行机调度问题. 图2 考虑设备可靠性的调度方法所节约的成本 比较9组算例的成本值可以得出以下结论: (1)相对于不考虑设备可靠性的调度方法,本文所提出的调度决策成本较低.随着设备初始可靠性偏差程度的增大,节约的成本值也随之增加,当b分别取0.1,0.3,0.5时,总成本分别降低了0.60%,1.29%,2.04%.这主要是因为考虑了设备可靠性后所得到的调度序列更加合理地分配了加工任务. 图3 可靠性偏差程度b对应的总成本 图4 可靠性偏差程度b对应的延迟成本比例 (2)相对于不考虑设备可靠性的调度方法,本文方法所节约的成本随着问题规模的增加而增大.如设备数量为5时,加工任务取50,60,70时分别节约了1.17%,1.49%,1.66%的总成本.这表明当问题规模增大时,在生产调度中考虑设备可靠性更有意义. 4.3.3敏感性分析 (1)设备初始可靠性对调度决策的影响.首先取9组不同算例验证初始可靠性的偏差程度对加工任务分配的影响,取T=0.4代表交付期较紧的情况.每组算例分别计算b取0.1,0.2,0.3,0.4,0.5时的结果,对比5种情况下总成本O,以及延迟成本在总成本中的占比Γ,结果如图3和4所示. 从结果中可以看出,随着b的增加,生产总成本几乎保持不变,但延迟成本的占比随之升高.这是由于,随着设备初始可靠性的偏差程度增加,对任务进行分配时会更加优先考虑设备可靠性.初始可靠性较低的设备将会加工数量更少的任务或者工时较短的任务,且初始可靠性偏差程度越大,设备间的加工时间差异越大.这样的任务分配方式牺牲了一定的交付期限,带来了更高的延迟成本,但却降低了更多的能耗成本.相较于传统不考虑可靠性的调度,这样的任务分配原则更加有利于降低生产总成本. 此外,当b由0.4变为0.5时,延迟成本比例变化较大,这表明当设备初始可靠性偏差程度很大时,任务分配对设备初始可靠性偏差程度的变化更敏感. (2)交付期对调度决策的影响.为了分析交付期松紧程度对于调度决策的影响,取b=0.5,令R=0.4,分别计算T取0.1,0.2,0.3,0.4,0.5时,延迟成本在总成本中的占比Γ′,结果如图5所示. 图5 交付期松紧对于调度决策的影响 由图5可见,随着T的增大,任务交货期变紧,延迟成本比例随之升高,各设备累积加工时间趋于一致,且T越大变化趋势越明显.分析结果可以得出以下结论: 当T≤0.3 时,加工任务的交付期较松,产能压力较小,此时初始可靠性较高的设备承担了更多的加工任务,大幅降低了能耗成本,有效地节约了生产总成本. 当T>0.3时,交付期较紧,过度关注能耗成本将会带来较高的延迟成本. 以上分析表明:在实际生产调度决策时,当交付期较松时,交付期不是降低成本的瓶颈因素,此时关注设备可靠性对生产调度的影响可以有效降低生产成本;而当交付期较紧时,则应主要关注延迟成本对于总成本的影响. 本文研究在平行机调度问题中设备可靠性对设备能耗成本的影响,建立了最小化延迟成本和加工能耗成本的数学模型,设计开发了蚁群算法求解问题,为车间降低总生产成本提供了新的思路.实验结果证明,本文提出的算法能够快速有效地求解所研究问题,相比不考虑能耗成本的调度方法,最多可降低2.5%的生产总成本,具有实际应用价值.此外,敏感性分析表明:当交货期较松时,将加工任务分配给可靠性较高的设备可以有效地降低系统成本;而当交货期较紧时,则应在保证不造成过高延迟的情况下进行任务分配.这一结论为车间基于设备可靠性进行生产调度决策提供了理论依据.在后续的研究中,将增加维护决策,以达到改善设备状态,提高设备的可靠性的目的,但是增加维护决策将进一步增加模型的复杂度和求解难度.4 算例验证与分析
4.1 参数设置


4.2 小规模算例验证
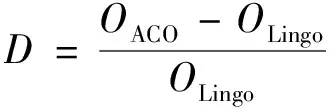

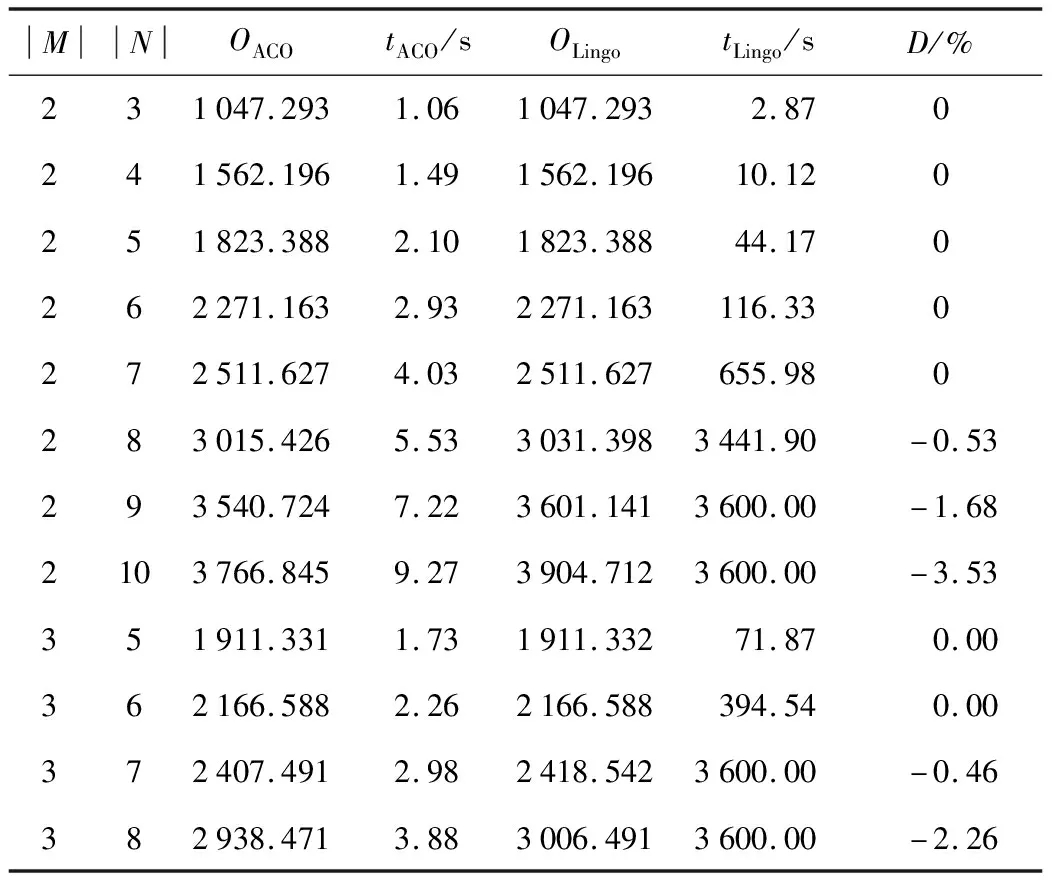
4.3 大规模算例验证

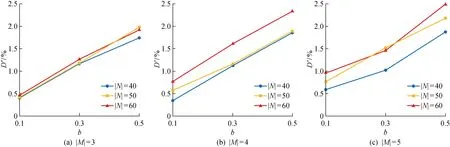


5 结语
