一类时标模糊微分方程的可解性
2020-04-08梅倩倩洪世煌丁方莉
梅倩倩,洪世煌,丁方莉
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
近年来,许多学者对时标微分方程进行了大量研究,有多值函数在时间标架上的可微性和时标上的集值方程与模糊方程[1-2]。其中,C.Vasavi等[2]利用Banach压缩原理,给出了时标模糊动力方程解唯一的充分条件。Hong S.H.等[3]研究了一类新的非线性脉冲集值动力方程,即时标上脉冲集值动力方程,并获得了该方程解的存在和稳定性的一些新判据。受以上研究的启发,本文首先定义模糊函数的广义导数,然后采用文献[1]中定义的集值函数的指数二分法,给出了模糊函数的相应概念,并探讨了时标上的脉冲模糊微分方程的可解性。
1 预备知识
时间标架T是实轴R上的一个非空闭子集,定义前跃算子σ∶T→T为:σ(t)=inf{a∈T∶a>t},后跃算子ρ∶T→T为ρ(t)=sup{τ∈T∶τ 定义1设Tf为T的所有模糊子集组成的集合,如果u∈Tf满足以下条件,即u∶T→[0,1]且 (1)u是正规的,即存在s0∈T使得u(s0)=1; (3)u在T上是上半连续的; 则称u为一个模糊数。 注意T⊂Tf。关于模糊集的更多概念见文献[4]。 定义2设集合X,Y∈Tf。如果存在Z∈Tf,使得X=Y+Z,则称Hukuhara差X-HY存在,且X-HY=Z。广义差“-g”定义为 CB(E)表示度量空间(E,d)的有界闭子集全体,在CB(E)上定义Hausdorff距离[5]为 定义3[2]设函数F∶T→Tf,t∈T,如果存在G∈Tf,使对∀ε>0,存在t的邻域UT=(t-δ,t+δ)∩T,(δ>0),当t+h∈UT,有 其中,μ(t)=σ(t)-t,则称F在t处广义可导。并称G是F在t处的广义导数,记作G(t)=ΔgF(t)。若F在区间I⊂T的每一点处广义可导,则称F在I上广义可导。 PC1=PC1[T+,Tf]={U∈BC|U在每一个区间(tk-1,tk)上广义可导} 考虑脉冲模糊微分方程 (1) 用eA(t,s)Us表示以下线性齐次模糊方程 (2) 的唯一解U(t,s,Us),其中初值s∈T+是固定的。∀u,v∈T,如果T=R,则eA(u,v)=eA(u-v);如果T=Z,且eA(u,v)=(I+A)u-v。其中I是满足正规性的模糊函数,Z是整数集。 (3) 则称方程(2)在时标T上满足指数二分法。 需要以下假设 其中τ,t∈T+。一般来说,对于a,b∈R及U∈Tf,(a-b)U≠aU-gbU。 如果函数F(t)是Δ可微的,且满足FΔ(t)=f(t),那么f定义在T上的(柯西)积分如下 (4) (5) (6) P1=(I-P)。 通过定义4和文献[1]中的引理11可得: (7) (8) (9) (10) 假设,对任意的正常数m,tm≤t≤tm+1,凭借条件(ii),可得 (11) 将式(11)中的2个不等式带入式(9)和式(10),可得 (12) (13) (14) 其中,tk≠t∈(t0,∞)T+。对于t∈[0,t)T+,通过文献[1]中的引理12可得: (15) (16) (17) 最后,在指数二分法的假设下,线性齐次模糊动力方程ΔgU(t)=A(t)U(t)的零解在T+上是有界的唯一解[6],设U1,U2都是线性脉冲模糊动力方程(4)的解。由式(4)的第1个方程可以推出: ΔgU1(t)-gA(t)U1(t)=ΔgU2(t)-gA(t)U2(t)=F(t)t≠tk (18) 本文在时标上给出了模糊微分方程解的唯一性。在证明解的唯一性时,采用指数二分法,并借鉴一类在时标上的脉冲集值微分方程解的存在性的研究方法。但是,本文只研究线性齐次模糊微分方程,相关非线性模糊微分方程解的定性问题有待进一步研究。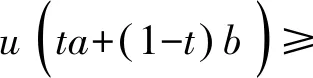
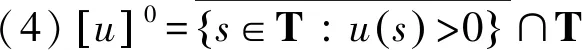

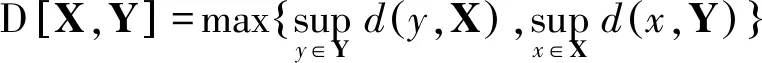
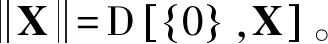
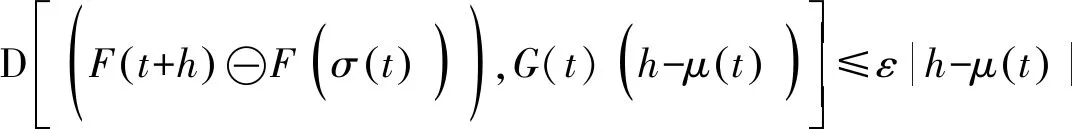
2 脉冲模糊微分方程的解

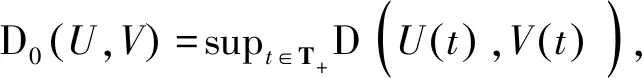

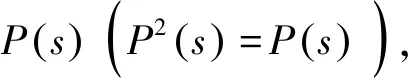
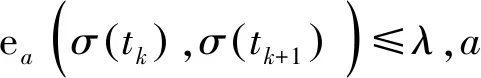
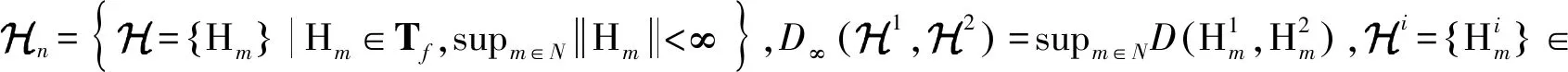
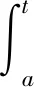

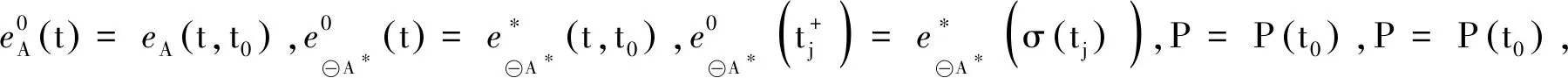

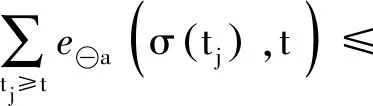

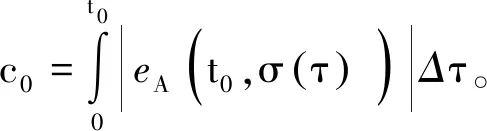
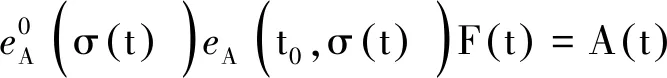
3 结束语
