观测站误差下外辐射源雷达TS-WLS定位算法

周夏磊，左 燕，蒋陶然

(杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

外辐射源雷达通过第三方(广播、电视、卫星、通信基站等外辐射源)发射的电磁信号辐射源对“无线电静默”目标进行探测与定位，具有隐蔽性高、抗干扰能力强、监视范围广、成本低等优点，逐渐成为雷达探测领域的研究热点[1-2]。外辐射源定位系统对目标监测通道的回波信号和参考通道的直达波信号进行相关性处理，得到信号的到达时差(Time Difference of Arrival, TDOA)。TDOA定位求解过程就是从TDOA量测非线性代数方程中解算出目标的位置。目前，基于目标辐射源的TDOA定位问题已得到广泛研究。文献[3]首先提出一种基于两步加权最小二乘估计的辐射源TDOA定位算法。随后，观测站位置误差[4]和时钟偏差[5]下的TDOA改进算法被相继提出。与目标辐射源定位体制不同，外辐射源雷达采用双基/多基结构，TDOA参数转化为双基距(Bistatic Range, BR)，具有强非线性，使得基于BR的目标定位估计难度增加。基于极大似然估计的BR定位可获得最优估计，但该方法计算量随变量维数的增加呈指数增长[6]。为此，基于加权最小二乘(Weighted Least Squares, WLS)[7]、两步加权最小二乘(Two-stage Weighted Least Squares, TS-WLS)[8]和约束总体最小二乘(Constrained Total Least Squares, CTLS)[9]的单站外辐射源雷达BR定位算法被相继提出。随后，文献[10]针对多站多外辐射源雷达BR定位问题，提出一种三步加权最小二乘估计算法。上述定位算法中，均假设观测站位置精确已知，但实际中的观测站位置往往存在扰动误差，直接影响目标位置估计的精度。因此，针对外辐射源雷达定位问题研究时须考虑观测站位置误差。

本文研究观测站位置误差下单站外辐射源定位问题，将多步加权最小二乘思想应用到定位模型中，提出一种改进的两步加权最小二乘估计的代数解算法，将观测站位置量测扰动噪声统计特性融入定位算法中，提高了算法的抗噪性和定位精度。

1 定位算法

1.1 问题描述

图1 单站多外辐射源定位场景

(1)

令BRD量测向量u=[u1…uM]T，BRD量测误差n=[n1…nM]T且协方差矩阵E[nTn]=Qn。基于BRD的单站外辐射源目标定位问题是根据BRD量测u和观测站位置量测Sr估计目标位置Star。

1.2 改进两步加权最小二乘估计算法

(2)

对式(2)两边平方，将R，rm和dm代入式(2)，展开移位可得：

(3)

(4)

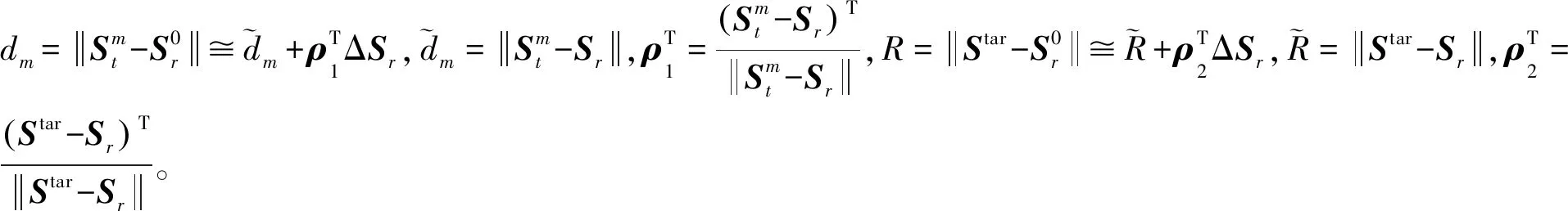
将式(4)写成矩阵形式

ε1=Z1-H1X1=A1n+B1ΔSr

(5)

X1的加权最小二乘估计值为

(6)

(7)

(8)

(9)

(10)

ε2=Z2-H2X2=A2ΔX1+B2ΔSr

(11)

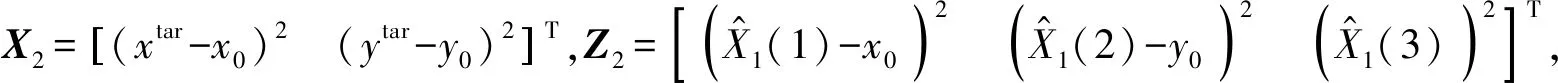
采用加权最小二乘估计求解式(11)，可得：

(12)

(13)

(14)

(15)

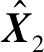
(16)

2 理论分析

2.1 克拉美罗下界

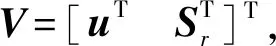
(17)

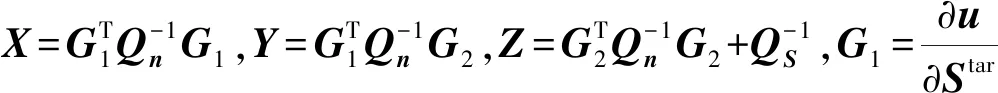
CRLB(θ)=X-1+X-1Y(Z-YTX-1Y)YTX-1

(18)

式(18)为考虑观测站位置误差时目标位置估计CRLB，第一项X-1是没有考虑观测站位置误差时目标位置估计CRLB，第二项则反映了观测站位置误差对目标定位CRLB的影响。

2.2 理论估计误差方差

根据一阶小扰动分析，得到本文提出的TS-WLS算法理论估计误差方差为

(19)

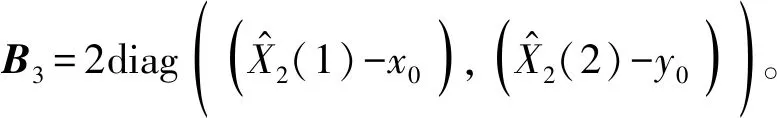
将式(7)，式(13)，式(15)之和代入式(19),可得：

(20)

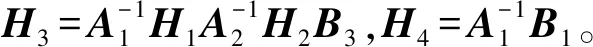
根据矩阵求逆公式，式(18)中CRLB的逆为

(21)

当观测站量测噪声误差适中时，H3=G1且H4=G2，式(20)与式(21)相等，说明本文TS-WLS算法的理论估计误差方差可以达到CRLB，定位精度高。

3 仿真测试与分析

(22)

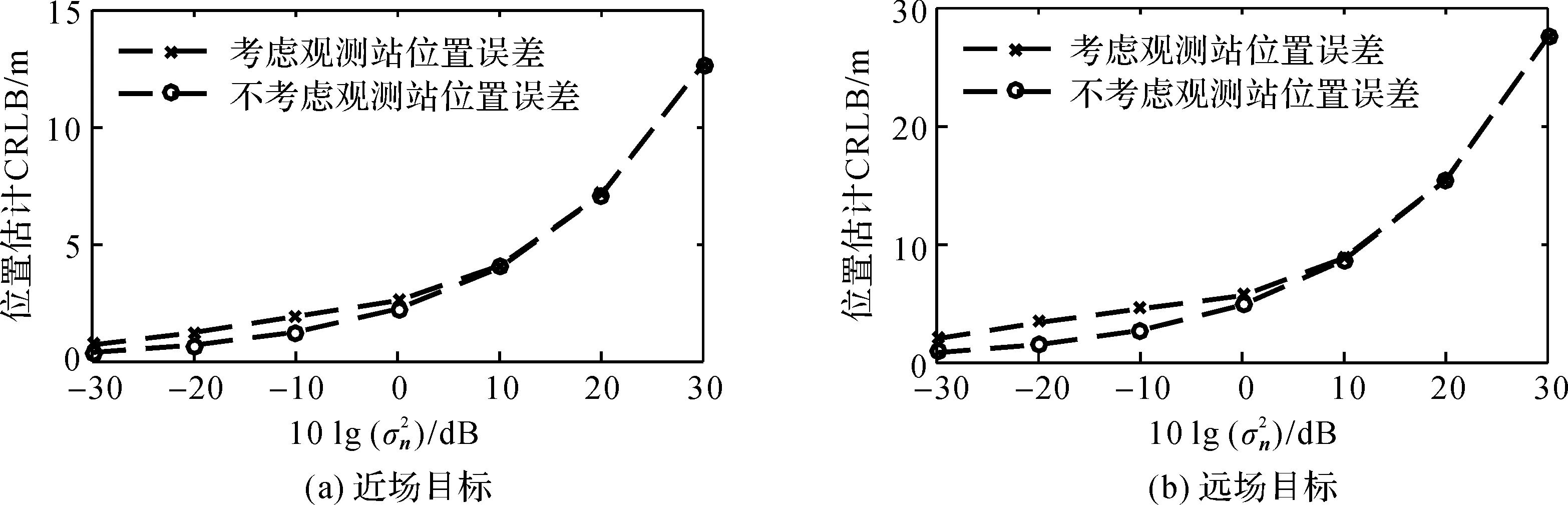
图2 不同BRD量测误差下目标定位CRLB

图3 不同观测站位置误差下目标定位CRLB

将本文TS-WLS算法与WLS算法[7]进行比较。在不同观测条件下，分别对近场目标和远场目标进行定位。仿真结果如图4和图5所示。

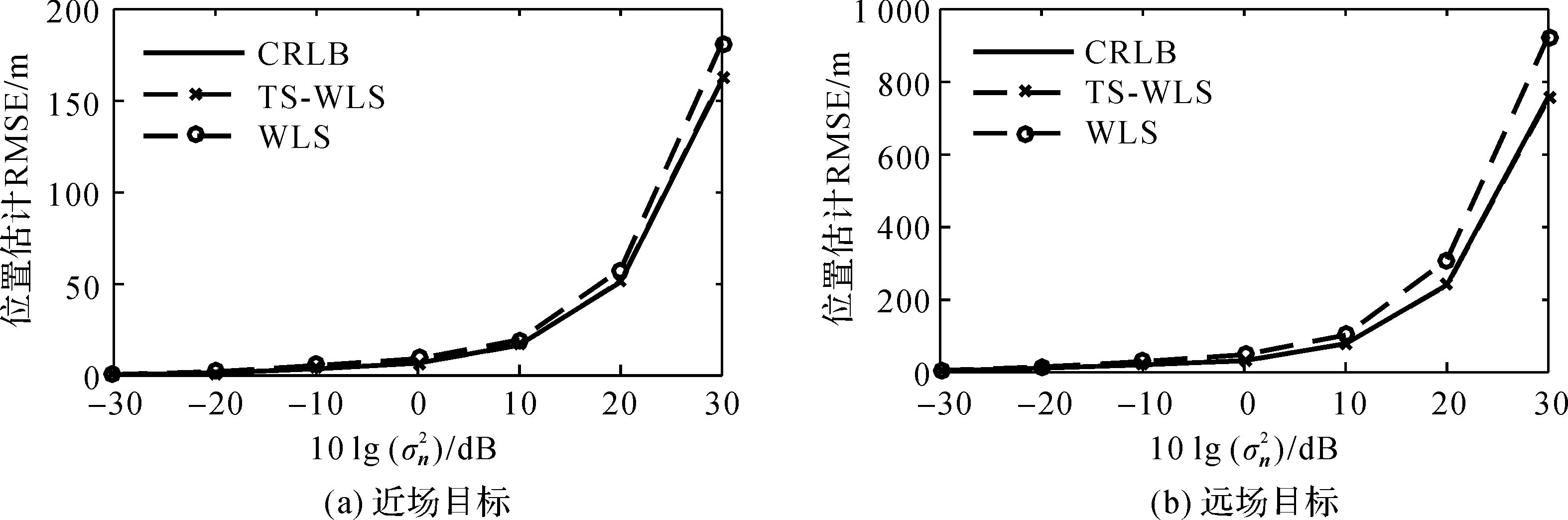
图4 不同BRD量测误差下定位算法估计性能

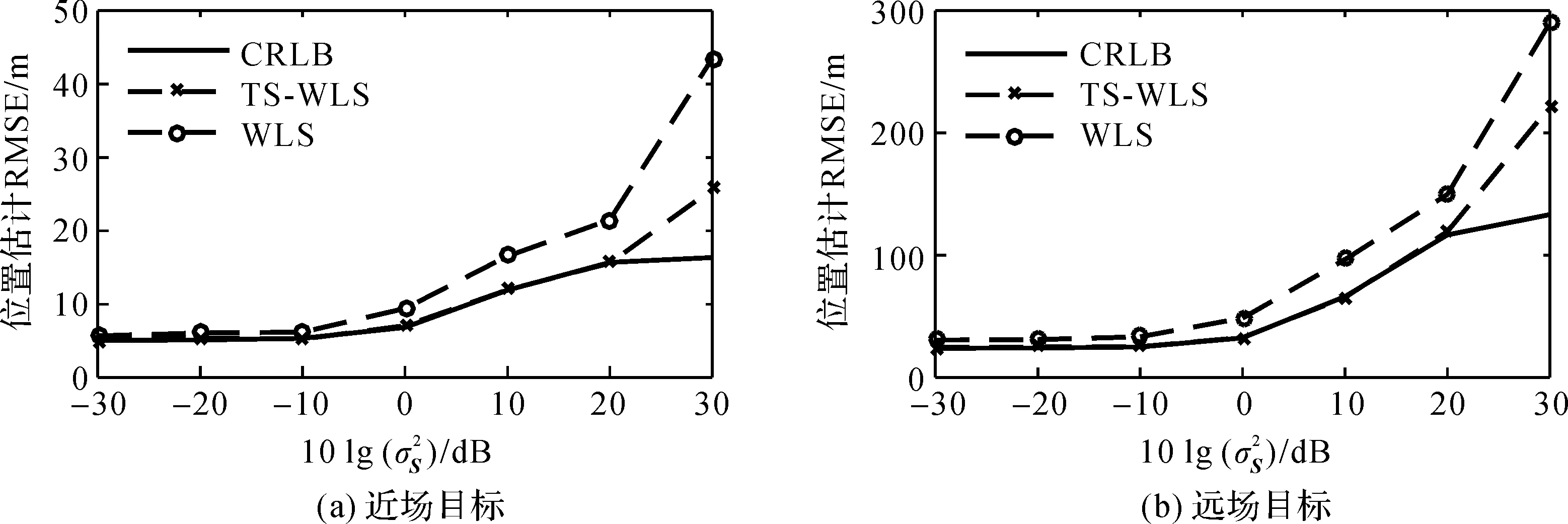
图5 不同观测站位置误差下定位算法估计性能

由图4可以看出：TS-WLS算法对目标的定位精度优于WLS算法，其定位RMSE均能达到CRLB。对于近场目标，当BRD量测误差大于10 dB时，WLS算法定位RMSE开始偏离CRLB。对于远场目标，当BRD量测误差分别大于-10 dB时，WLS算法定位RMSE开始偏离CRLB。相同的BRD测量误差下，远场目标的定位误差比近场目标的定位误差更大。

由图5可以看出：TS-WLS算法对目标的定位精度优于WLS算法。对于近场目标，当观测站位置误差为-20 dB时，WLS算法定位RMSE开始偏离CRLB，当观测站位置误差升至20 dB时，TS-WLS算法定位RMSE才开始偏离CRLB；对于远场目标，当观测站位置误差为-30 dB时，WLS算法定位RMSE开始偏离CRLB，当观测站位置误差升至20 dB时，TS-WLS算法定位RMSE才开始偏离CRLB。相同的观测站位置误差下，远场目标的定位误差比近场目标的定位误差更大。

比较TS-WLS算法和WLS算法的计算复杂度。TS-WLS算法计算复杂度为O{NP[2(D+1)M2+2(D+1)2M+(D+1)3+(D+1)M]}，WLS算法计算复杂度为O{NP[2(D+1)M2+2(D+1)2M+(D+1)3+(D+1)M+2D(D+1)2+2D2(D+1)+(D+1)3+D(D+1)]}。二维空间下D=2，M为外辐射源个数，NP为计算加权矩阵时的重复次数，NP=2。在1 000次蒙克卡洛仿真中，TS-WLS算法平均运行时间为0.026 s，WLS平均运行时间为0.010 s。两种算法计算收敛速度很快，TS-WLS算法运算量比WLS算法略有增加，但定位性能则有显著提高。

4 结束语

本文研究了观测站位置误差下单站外辐射源雷达双基距定位问题，提出了一种改进的两步加权最小二乘的代数闭式解算法。算法将观测站位置量测扰动噪声统计特性融入到定位算法中，提高了算法抗噪性和定位精度，计算效率高，有一定的工程应用价值。但是，本文算法针对的是单站多外辐射源定位场景，下一步将对多站多外辐射源定位问题展开研究。