开放式小区公交微循环站点与线网综合设计

邓吉浩，宋 瑞，陈小鸿，王天实，王柏豪

(1. 同济大学 道路与交通工程教育部重点实验室，上海 201804；2. 北京交通大学 城市交通复杂系统理论与技术教育部重点实验室，北京 100044；3. 清华大学 土木工程系交通研究所，北京 100084；4. 加利福尼亚大学戴维斯分校 交通运输研究所，戴维斯95616，美国)

城市公交微循环是交通微循环在公共交通上的应用，可以及时疏散交通流量，也可以保证公共交通系统的快捷高效性.随着城市的快速发展，土地的储备日渐稀少、道路供给日趋不足，这也成为当今我国大城市交通拥堵的主要原因之一.生活在被围墙包络的“封闭式小区”的居民对居住环境的要求不断提高，对活力街区的诉求日益明显.因此，2016年国务院曾发布《关于进一步加强城市规划建设管理工作的若干意见》[1](以下简称《意见》)指出：应推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院要逐步开放，即规划、构建“开放式小区”.在开放式小区背景下，综合设计公交微循环的站点和线路对于改善居民生活质量、提高城市交通系统的运行效率、降低公交企业的运营成本等具有至关重要的作用.

国外城市对微循环线路的研究较为成熟，Supangat等[2]为减少西雅加达居民区的交通拥堵，利用平均偏移聚类方法实现了对最佳巴士站位置的选取.Sha等[3]基于公交微循环系统的便捷性，提出了可以同时考虑减少乘客至公交站点步行距离和提升公交可达性的模型，并求解出最优站点位置.Pang等[4]建立双层规划模型，考虑弹性需求布设城市公交站点.Kuah等[5]综合考虑运营商和用户的成本，设计了从机场或远郊购物中心到城市中心区的接驳巴士线路.Lin等[6]提出了一种“反馈线路”模型，能够最小化公交线路长度，最大限度减少车辆运行时间并提高车站的服务范围.Pattnaik等[7-8]利用遗传算法实现了对现有线网的局部优化.

近年来，国内对公交微循环的站点布设、线路设计方法以及求解算法上都有所发展.张锐[9]应用集合覆盖方法实现了对公交站点的选取.武苗苗等[10]基于公交客流特性，分析了微循环背景下的公交站间距取值.魏强[11]以线路客流密度最大为目标建立模型，对公交微循环线路进行设计.潘述亮等[12]以满足乘客个性化需求为导向，提出了灵活型公交微循环系统设计理论及方法.熊杰等[13]基于公交潜在需求指标构建了社区公交路径优化模型.刘华胜等[14-15]综合考虑乘客与企业利益，建立双层模型以解决接运线路设计问题.孙志田等[16]用改进遗传算法求解公交线网的优化模型.解超[17]综合利用多路径最大覆盖/最短距离模型(MSMCSP)和逐条预选与搜索优化(PSO)算法、设计了快速公交的选线方案.赵胜川等[18-19]分别利用最短路及k-最短路算法和免疫遗传算法，实现了对公交线网的优化.

现有的研究针对站点布置和线路设计考虑了不同因素，建立模型并设计了求解算法，但是均未考虑在开放式小区背景下可利用小区内部道路进行公交微循环布设；此外现有研究只单独考虑站点选址或线网布局，没有将二者进行综合设计.本文作者基于开放式小区，建立了能够同时考虑站点和线路设置的微循环公交综合设计模型.利用遗传算法，得到了所选算例小区的微循环公交站点与线路设计结果，并给出了使企业和乘客利益达到最优的参数取值.

1 选点与选线的相关因素分析

建立综合设计模型需要明确与站点选址与线路布局的相关影响因素.这些因素可以成为所建模型的约束条件，另一方面也可以对模型求解结果的合理性与有效性做出评价.叶秋君等[20-21]在研究公交站点选址与线路设计问题时，根据乘客需求、运营调度、社会财政等提出指标并进行了定性或定量分析.本文基于此并结合研究背景，主要考虑以下影响因素:

1)站间距与线路长度.和常规公交类似，公交微循环的站间距需要控制在合理的范围内，过长的站间距会降低乘车便利性，过小的站间距则增加运行成本并有损乘客乘车舒适度.

2)服务区域.常规公交站点的布设一般会考虑其服务区域内的土地利用，居民出行需求密度越大的区域，越有可能设置公交站点.公交微循环线路的布设不需要将用地性质作为主要因素考虑，但可以利用类似的方法寻找乘客乘车需求较大的“需求点”，进而建模求解.

3)线路条数.对一确定的服务区域，公交线路的布设条数应在合理的区间.过多的线路条数会增加运营公司的成本，在非高峰时期造成资源的浪费；线路条数过少则会损害乘客的乘车利益.

此外，车辆配置、运营的时间可靠性、运营的安全性以及相关政策与票价等因素均会影响公交微循环系统.这将为进一步深入研究提供思路.

2 站点与线路综合设计模型

2.1 问题描述

开放式小区公交微循环站点与线路综合设计问题可以描述为：对给定的已知数量的小区，根据居民出行需求调查确定需求点的位置与数目，在已知公交微循环线路数目的条件下，结合乘客的步行距离约束确定公交站点的位置与数目，同时根据站距范围约束和线路闭合约束得到最终微循环线路布设结果，每一条线路均为圈点线路，以满足居民的出行需求，并实现企业成本和乘客成本的最小化.

2.2 模型假设

1)所研究的每个小区内部道路均具有公交车通行条件；2)所研究区域内机动车之间、行人之间无相互影响；3)所研究问题的总成本与企业成本和乘客出行成本线性相关；4)所研究区域周边只有1个地铁站.

2.3 模型参数

模型参数符号及含义见表1.

表1 模型参数符号及含义

2.4 模型表述

开放式小区公交微循环站点与线网综合设计模型如下：

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

zmi≤yi

(7)

(8)

(9)

(10)

zmi·dmi≤smax

(11)

(12)

3 算法设计

本文建立的模型为0-1整数规划模型.遗传算法可以有效求解此类问题，故采用遗传算法对模型进行求解.

3.1 个体编码方式

应用多段组合染色体编码，将染色体进行整数编码.一条染色体由表示每条线路的基因段组成，每条基因段由0及若干自然数组成，其中基因段开头和末位的“0”为线路起讫点，其他“0”为空位不表示任何含义，非0整数表示该线路途经的站点序号.

模型中的式(2)～式(5)及式(7)规定了线路的形状和特性，该算法编码的目的在于检查所设计的线路是否符合其他约束条件，若不符合，则重新编码.

在编码染色体前，先对各备选站点进行编号，以4条线路12个备选站点为例，染色体编码示意见图1.图示中所对应的4条线路分别为：O(地铁站，公共起点)→10→12→O；O→7→2→8→O；O→1→3→6→O；O→4→9→5→11→O.

3.2 选择、交叉、变异

1)选择.采用最佳个体保存与轮盘赌选择相结合的策略.具体步骤为：首先计算并给每代种群个体的适应度进行排序，排序后第一条染色体为适应度最高的个体予以保留；其余根据前代种群个体适应度，采用轮盘赌选择策略进行运算.

2)交叉.染色体的交叉操作采用单点交叉方式.

3)变异.按照预设变异概率，随机将染色体的基因变异成为站点序号范围内的任意一点，变异之后对所得染色体进行检测，若不符合条件便重新变异，直到可行为止.若无需调整，则变异结束.

3.3 不可行解处理方法

建立判断函数，函数值规定为0-1变量，染色体若符合所有约束条件则函数值返回1，若不符合任意约束条件则函数值返回0.当判断函数运行结果为0时，启动编码函数，将不符合约束条件的染色体重新生成.

4 算例分析

北京回龙观地区有大量住宅用地，某小区位于该地区最北端，小区周边有3个公交车站，但分布分散、距离小区现有出入口较远.该小区东侧820 m处布设有地铁平西府站(8号线)，经过实地考察，若将该小区内道路用地计算在内，该区域的道路面积率超过15%，该小区所在街区平均面积低于5万m2，符合《意见》的相关要求[1]，该小区已具备转变为开放小区的基本条件.因此，选取该小区作为研究对象，验证上述模型和算法的正确性和有效性.

4.1 算例数据

该小区现有西门、南门2个出入口.小区内部道路均具备消防通道条件.经过实地考察，获得了小区居民在高峰时间段出行需求的数据，结合小区内道路的设置情况和住宅楼的分布情况，通过在某周三(工作日)进行居民出行调查，识别在早高峰时间段居民在小区内高频出现的150个位置，即所考虑的需求点.根据这些需求点的位置作聚类分析，得到25个车站备选点，最终期望得到的车站实际位置将从这些备选站点中产生.取站间距下限smin=200 m，站间距上限smax=400 m(不包括实际站点和地铁站的距离)，线路条数M=4.

4.2 求解结果与分析

输入算法参数为：迭代次数MAXGEN=200，种群规模SIZEPOP=50，交叉概率Pcross=0.9，变异概率Pmutation=0.09，线路条数M=4，α=0.4,β=0.6.在Intel Core i5-2450M CPU @ 2.50 GHz，内存8 G，操作系统 Windows 10 环境下，使用数学求解器Matlab R2015b求解50次，每次均可获得对应种群下的最优解，且每次求解运行时间均少于15 s.从Matlab的运算结果中调取Individuals数据表，对50次结果进行比对分析，得到一组最优解.该解的4条线路分别为：

①O(地铁平西府站，下同)→1→7→11→23→O；

②O→8→5→9→14→15→O；

③O→12→13→21→25→O；

④O→10→17→18→19→20→O．

得到的公交微循环站点选址和线路设计方案见图2.绘制收敛函数曲线，见图3.由图3可知，在100代后算法收敛.

通过计算直线距离，可以得到线路布设前后的居民总步行长度，对比后可以发现线路布设前居民从所有需求点步行至小区南门、东北门及西门距离共15 342 m，大于线路布设之后居民步行至最近微循环线路站点的距离共3 219 m，也证明了微循环线路的设置可以有效减少最后一千米的步行距离.

需要说明的是，尽管Lingo算法可以给出最优解，但使用Matlab遗传算法完成求解的时间远远小于Lingo算法.此外，当线路条数M≤2时，Lingo算法可以在有限的时间内给出一个最优解；当线路条数M>2时，针对每个M值都分别进行10次运算，发现使用遗传算法更节省时间，其得到的最优解与使用Lingo算法得到的最优解的差值在允许范围内，使用Lingo算法和使用Matlab遗传算法计算结果的比较如表2所示.表2中对比度=(Matlab遗传算法计算结果-Lingo算法计算结果)/Lingo算法计算结果×100%.

由表2可知,遗传算法在求解该问题时比Lingo算法更具优势.

表2 使用Lingo算法和使用Matlab遗传算法计算结果比较

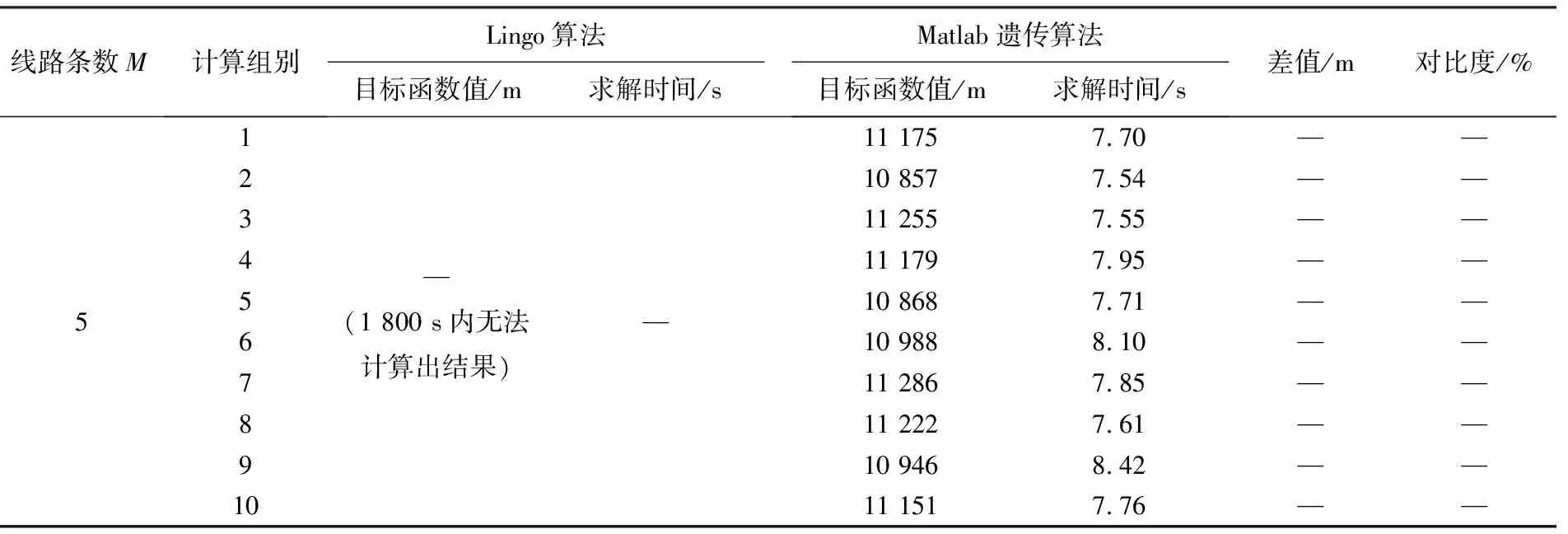
续表2

4.3 灵敏度分析

为了向决策者提供支持，以下对公交企业成本权重α、乘客出行成本权重β以及线路条数M进行灵敏度分析.

1)对α和β进行灵敏度分析.

对α、β分别取4组值，并针对每组权重值对不同线路条数M计算目标函数值(该值为使用遗传算法运算20次的平均值)，不同α、β值下的目标函数值见表3.

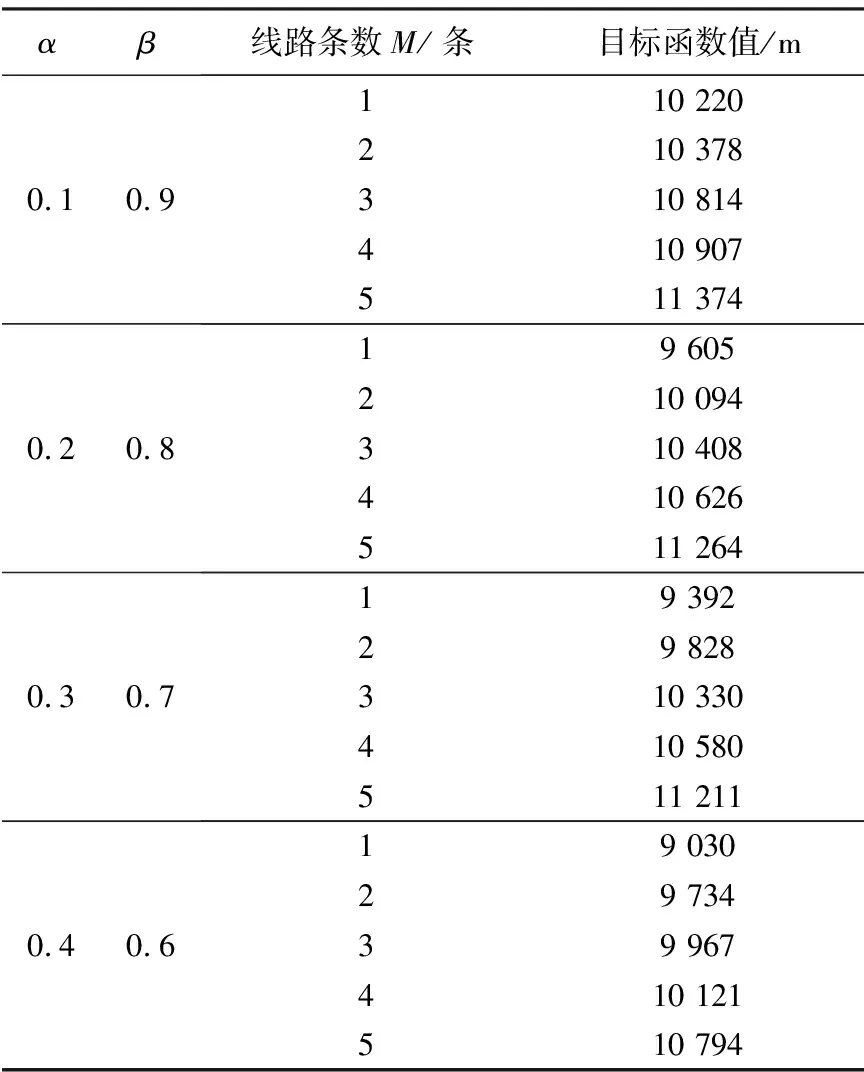
表3 不同α和β值下的目标函数值

在以上算例中，当α的值不断增大时，相同线路条数对应的目标函数值不断减小，表明较大的α值对应的最优解更有优势，可以使得公交公司的成本和乘客出行成本的总和达到最优，因此可以设定α=0.4,β=0.6.

需要说明的是，当针对的研究区不同时，需求点的位置与数量也不同，在不同的α与β的取值下得到的结果及其变化趋势可能不同，最后得到的设计结果也会有不同.因此在实际规划中，决策者应根据具体要求输入参数α、β，进而找到使目标函数值最优的权重值组合.

2)对线路条数M进行灵敏度分析.

乘客利益和运营企业利益不同，乘客希望省时、便捷；企业则希望减少线路条数以减少运营成本.当α、β取不同值时，企业运营距离成本和乘客出行距离成本随线路条数M的变化曲线见图4.

由图4可知，当α、β取值相同时，乘客出行距离成本随线路条数增加而减少，企业运营距离成本随线路条数增加而增加.因此，决策者在选定参数α、β值后，应综合考虑企业与乘客利益，合理布设线路条数.

5 结论

针对开放式小区公交微循环站点与线路综合设计问题进行了研究，建立了公交微循环站点和线路综合设计模型，编写了遗传算法，通过逐步迭代获得近似最优解.得到以下结论：

1)模型以所有公交微循环线路总长度最小和乘客总步行距离最短为目标函数，同时将站点数量、站间距范围、线路长度范围等作为约束条件.

2)实际案例验证了模型与算法的有效性与正确性，也表明使用遗传算法能在更短时间内求解出有效、合理的站点选址和线路布设方案.

3)灵敏度分析表明，当α=0.4,β=0.6时，在相同线路条数下目标函数值更小，即所得解有明显优势.

4)在选择布设线路条数时，决策者应综合考虑企业与乘客利益确定.

作为对解决“最后一千米”问题的尝试，城市规划师和交通设计师可以考虑设置公交微循环线路，以服务居民的接驳出行需求.

随着乘客对于个性化出行需求的发展，公交微循环的运营调度方法和灵活型公交微循环线路设计方法将成为继续深入研究的课题.