考虑出行者选择偏好的出行方式选择模型

姚恩建，陈伟迪，卢天伟，杨 扬

(1.北京交通大学 a.交通运输学院,b.综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

随着城市的发展和社会经济水平的不断提高，城市交通系统日趋完善，出行方式也愈加丰富.长期以来，人们为应对多样化的出行需求，尝试建立多样的出行方式选择模型，以求客观准确地刻画出行者的出行行为.

在传统非集计模型研究领域，Algers等[1]通过SP(Stated Preference)、RP(Revealed Preference)调查数据并结合Logit模型进行出行选择行为分析.李鹏[2]针对多种交通运输方式的选择，加入了层次分析法进行辅助决策.随着大数据分析的广泛运用，刘阳等[3]基于深度神经网络，构建了描述城市交通出行方式选择行为的小波神经网络预测模型.

在不断修正和改进过程中，多项Logit(Multinomial Logit, MNL)模型因其概念明确、计算方便的特点，逐渐成为目前出行方式选择研究领域中运用最为广泛的方法.但MNL模型要求出行者选择结果的影响因素彼此之间无相互影响，这在现实条件下难以满足.针对该问题，Williams[4]提出了分层的多巢Logit模型(Nested Logit, NL)，在实际预测中很大程度上解决了MNL模型的不相关选择项独立性假设(Independence of irrelevant alternatives，IIA)特性.姚丽亚等[5]通过研究，进一步证明了NL模型在预测中具有更好的预测精度.杨励雅等[6]同时考虑了出行方式与出发时间，联合建立了NL模型，证实了NL模型优于MNL模型.因此，在后续的研究中，NL模型被更广泛地应用于出行行为选择研究中，同时也将作为本文模型构建的基础.

非集计模型建立的假设基于效用最大化理论，即出行者能够选择其备选方案内效用最大的出行方案[7].影响选择结果的特性包含交通方式特性和出行者特性，这些方式特性均为客观特性.而在实际出行情境中，不同个体对于客观特性的敏感程度表现不一，因此导致选择决策伴随一定的主观因素和随机性，对选择结果并不一定完全基于绝对理性[8].Simon[9]将该行为决策称有限理性满意决策.有学者开始尝试将影响决策变量的主观程度考虑进传统的MNL模型中，解释实际发生的出行方式选择行为.杨励雅等[10]为克服Logit类模型的局限性,以出行链为分析单元,构建快速城市化进程中居民出行方式选择的结构方程模型.景鹏等[11]为出行方式选择模型添加心理潜变量，以计划行为理论为框架，整合对通勤方式选择行为有影响的各种心理因素，通过估计模型参数预测心理潜变量的拟合值，并将其作为解释变量加入到传统Logit模型中形成混合选择模型.Krishnan[12]首次提出了效用差概念，以衡量影响出行者在不同出行方式间选择的影响因子，并进一步修正Logit模型，建立方式选择MPD(Minimum Perceivable Difference)模型.张新洁等[13]针对MNL模型的IIA特性缺点，结合效用差感知阈值理论，在连续平衡交通分配方式下构建有限理性分层Logit(Bounded rationality nested Logit, BRNL)模型，引入感知成本差，假设当感知成本差足够大时，出行者依据个人喜好做出选择判断.

上述研究已经证明引入主观因素对提高传统非集计模型预测精度的重要性.本文作者以传统NL模型为框架，通过引入度量偏好程度的参数，模拟出行者在选择出行方式时的决策过程，形成有限理性的方式选择模型，并结合案例检验其预测效果.

1 固有选择偏好特征

1.1 有限理性选择行为定义

理想状态下，出行者在选择出行方式时，会统筹考虑视野内备选出行方案的特征因素，例如不同方案的出行时间、出行费用等，并通过理性分析选择用户最优出行方式[14].然而在实际出行情景中，出行个体并非对备选方式的特征因素变化完全敏感，可能忽略细小变化，仅依据个人偏好做出不符合理性假设的选择[15].本文认为此类情景中的出行者处于对特征因素的不敏感区间内，其选择行为伴随一定程度的主观随机性和个人偏好.

1.2 选择偏好存在性验证及分析

为验证方式选择行为中存在非完全理性决策及不敏感区间假设的真实性，将基于SP调查的方式进行出行者的出行选择行为数据采集，并分析其选择行为特征.获得出行距离7～9 km的情境下，地铁和公交的出行时间调整后(增加或减少)的被调查者选择意愿变化.特征变量取值情况见表1.

表1 特征变量取值

本次SP调查对象以公共交通(公交、地铁)为主要出行方式的在校大学生(无车人群)，以互联网为传播渠道[16]，共收回符合条件的问卷数量为200份，经有效性判别、筛查后最终得到有效问卷数量为189份，调查结果显示交通方式的消耗时间与选择意愿存在一定相关性，如图1所示.

由图1可知，横坐标各条件下的平均值和四分位数显示出行者对地铁的选择意愿与时间差值成负相关趋势，即地铁出行时间越少，出行者更倾向于选择地铁出行.当时间调整幅度处于[-10,+15] min时，选择意愿的平均值和中位数没有显示出与时间调整幅度明显的相关性，而是呈现出相对稳定的情况，-10、-5、0、+5、+10 、+15 min条件下的四分位数分布体现了此时出行者对特征变量改变的敏感性较弱，其选择行为并非完全理性.因此，上述结果证明了出行者在出行方式选择时带有一定的个人偏好和主观随机性，本文将此类固有选择偏好和选择随机效应下的出行方式选择行为归为有限理性下的出行方式选择行为.

2 构建有理性的方式选择模型

2.1 改进NL模型结构

为描述选择情况，探究出行者出行时间、出行费用与出行方式选择之间的相关性，建立出行方式分层选择结构[17-18]，见图2.

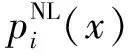
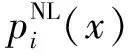
(1)

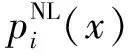
(2)

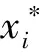
得到出行方式i的选择概率

(3)

2.2 出行方式选择概率计算方法

对于NL模型而言，选择水平1中任意方案ir的概率pNL(ir)等于选择水平2中r条件的概率pNL(r)与在r条件下选择i方案的概率pNL(i|r)的乘积，即

pNL(ir)=pNL(i|r)×pNL(r)

(4)

pNL(i|r)和pNL(r)的求解函数如下

(5)

(6)

(7)

式中：V(i|r)为在选择方案ir时，效用由于ir和r的组合而变化部分的固定项；Vr为在选择方案ir时，效用中与i无关，仅随r变化部分的固定项.Ir为在r条件下水平1中的选择方案数；R为水平2中的选择方案数；λ为尺度系数.

3 数据分析及模型参数确定

3.1 出行调查数据统计分析

本文所采用数据基于北京市第五次居民出行调查统计.为更为精准地研究选择偏好影响效果，将研究对象设定为以公共交通为主要出行方式的无车人群，并通过随机抽样的方式构建了20 996条出行方式备选集，其中,仅包括第2章中所提及5种交通方式的出行者调查数据样本，其相关影响因素包括出行费用、出行时间，具体的数据统计情况见图4.

3.2 建立方式效用函数

通过极大似然估计法对模型中各项的指标系数进行标定[20]，确定各效用函数的特征项和固定项，并对各项系数进行显著性检验，结果见表2.

表2 系数标定结果

调整优度比ρ2为0.393，大于0.2，说明模型拟合较好，尺度系数λ标定结果为0.537，介于0到1之间，说明模型结构合理.各参数的t值绝对值均大于1.96，说明各变量对效用函数值影响显著.将上述标定结果代入效用函数公式，得到基于本次调查数据下的各出行方式的效用函数表达式：

Vwalk=3.20-0.067 3×Xtime1

(8)

Vbike=-0.372-0.082 2×Xtime2

(9)

Vbus=-0.015 7×Xcost1-0.069 4×Xtime3

(10)

Vsubw=-0.015 7×Xcost2-0.069 4×Xtime4

(11)

Vtaxi=-0.025 7×Xcost3-0.066 4×Xtime5

(12)

3.3 假设情景及变量取值

《第五次北京城市交通综合调查》显示北京市居民的日平均出行距离为8.1 km[21]，故以起讫点相距8.5 km的西直门地铁站、中关村地铁站为例.通过《2015年北京交通发展年报》[22]，可得2014年北京市晚高峰时段(17:00—18:00)5种出行方式的平均速度，见表3(公共交通的平均速度包括进出站及换乘).据此计算各出行方式的平均出行时间，作为特征变量固定值.通过百度地图API获取晚高峰时段各出行方式的实际出行时间、出行费用，作为模型计算选择概率的特征变量值.以《2015年北京交通发展年报》中的2014年北京市各交通方式出行量的比例，作为5种出行方式各自的固有选择偏好.模型中各变量取值见表3.

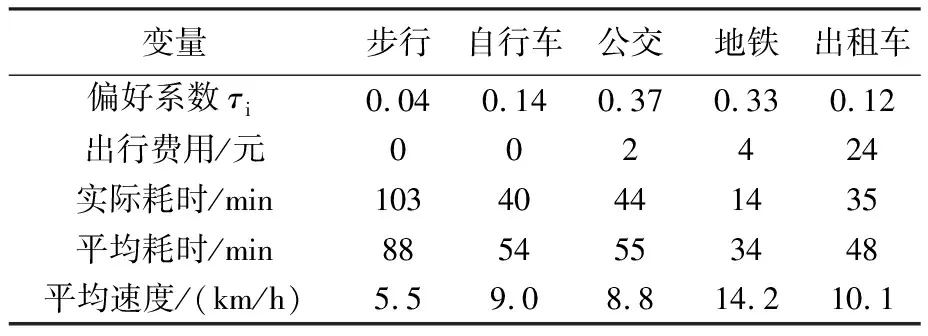
表3 模型中各变量取值

由于出行距离8.1 km已经远超第5次交通调查中步行的平均出行距离1.6 km，因此所得步行方式选择概率缺乏实际意义，在后续分析中仅反映步行方式受其他因素变化的影响情况.

4 模型结果分析

偏好程度σ值对地铁选择概率的影响见图5，其中地铁的最短出行时间为5 min.由图5可见，σ值可以用来反映出行者的选择偏好在选择行为中的作用强度，σ值越大，选择行为越具有偏好倾向.

从图5中可知：

1)NL模型计算出完全理性行为能力下地铁选择概率随出行时间变化的规律，出行时间增加，地铁选择概率降低，两者呈现较为直观的负相关性.

2)当σ=3时，出行者的选择行为变为有限理性.地铁出行时间在15～35 min内，其选择概率没有明显变化，此时的选择概率近似等于地铁的固有选择偏好0.33.在15 min之后的有限理性选择概率大于完全理性选择概率，在15 min之前的有限理性选择概率小于完全理性选择概率.

3)当σ=5时，随着地铁出行时间增加，地铁的选择概率始终是0.33左右.也就是说，出行者理性程度非常低，其选择行为基本不受时间变动的影响，完全依据个人喜好选择.

结合图1、图5，当σ=3时，出行者对于地铁出行时间的不敏感区间在[-10,10] min，和实际调查结果相似，因此取σ=3，得到地铁出行时间对各方式选择概率的影响关系见图6，由图6可知：

1)随着地铁出行时间增加，地铁方式的选择概率逐渐降低，其他方式的选择概率有不同程度的增加.说明乘坐地铁出行需要的时间越长，出行者选择地铁的概率越低，此时出行者更倾向于向其他交通方式转移.

2)地铁及其他出行方式的选择概率，在出行时间为25 min上下范围内的变化趋于稳定.说明对于选择地铁出行的出行者，出行时间在25 min上下范围内时，其选择行为受固有选择偏好影响，选择行为趋于有限理性，而受时间变化的影响程度相对较弱.

3)当地铁出行时间超过35 min后，地铁的选择概率继续随出行时间增加而降低.说明此时出行时间超过了出行者的心理承受范围，其选择行为重新趋于理性，在选择出行方式时会理性考虑时间价值.

随机抽取出行距离在8 km左右的500组数据，代入模型，计算得到NL模型和有限理性模型的预测结果见表4，命中率检验结果见表5.由此可知：

1)对于步行、自行车和公交选择概率的预测结果，有限理性模型的预测概率比NL模型更高；而对于地铁和出租车，有限理性模型的预测概率比NL模型更低.

2)传统NL模型预测的步行、自行车的选择概率误差更小，真实性更高；有限理性选择模型预测的地铁、公交及出租车的选择概率误差更小，真实性更高.

3)有限理性模型在5种方式上的结果命中率均高于传统NL模型，体现了更好的适用性和更高的预测精度.

表4模型预测的出行分担率结果

Tab.4Split rate predicted by the model of travel mode selection %

出行方式有限理性模型NL模型真实值步行3.51.90.7自行车109.57.5地铁32.332.926.3公交31.429.941.4出租车22.725.724.1

表5命中率检验结果

Tab.5Test results of hit rate %

出行方式NL模型有限理性模型步行81.1282.84自行车82.0482.36地铁86.6387.05公交81.3684.97出租车83.7484.35

偏好程度σ值对各出行方式选择概率的影响见图7.由图7可知：

1)随着σ值的增加，出行者的理性程度逐渐降低，出租车的选择概率逐渐减小，其他交通方式的选择概率逐渐增加.

2)随着σ值的继续增加，出行者选择行为转变为完全非理性，各方式的选择概率逐渐趋于恒定，选择行为接近主观偏好，选择结果接近固有偏好系数.

3)地铁方式选择概率随σ值的变化较小，非理性选择结果和理性选择结果相似，说明地铁对出行者的黏度更高，在通勤场景中选择地铁方式的出行需求相对刚性.

5 结论

1)在NL模型中引入了固有选择偏好作为影响出行者出行选择行为的重要因素，与理性决策原则共同决定选择行为，使选择模型对于实际选择情况的预测更加精准.

2)交通方式的特征变量不再直接决定模型的计算结果.当备选方案的特征变量在特定区间变化时，出行者的选择行为体现出相对较强的个人偏好，选择概率几乎不随之变动.当特征变量的变化超出特定区间时，更多地体现出理性选择的特点，选择概率随特征变量的改变而变化.

3)通过对模型参数σ的估计，可以描述不同出行者在选择时的不敏感区间，准确预测复杂条件下的出行者方式选择结果，为出行方式选择行为相关研究提供理论基础，也为交通结构的合理调整提供科学依据.