区域轨道交通跨线运行行车密度优化模型

梁青槐，柴树山，邓京维

(北京交通大学 土木建筑工程学院，北京 100044)

截至2018年末，我国累计有35个城市建成投运城轨线路185条，运营线路长度达5 761.4 km，国内很多城市已进入网络化运营的阶段[1].其中，跨线运行有利于实现整个网络的线路资源利用效率和运营效率的最大化，可以提高客流服务水平[2]，是实现线路互连互通的重要方式之一.另外，区域快线与城际铁路相比，具有同城化通勤服务、公交化的城市轨道交通特征，与普通地铁相比，具有高速度、高服务范围等优势[3].因此，区域快线与地铁系统的跨线贯通运营对于实现中心城区与近远郊地区之间通勤客流的快速直达、减少换乘、缩短旅行时间等具有重要的作用.

国内外许多学者对网络化运行和区域轨道交通列车运行组织方案的编制与优化进行了相关研究.在网络化运行方面，仲建华等[4]针对轨道交通网络化运行的内涵、原则、思路和基本条件等进行了探索；张化难等[5]以重庆为例，探讨了网路化运行中的快慢车运行模式.在单线运行组织优化方面，Assis等[6]基于客流的动态变化，分析乘客的出行时间，分时段对列车的时刻表进行优化和排定；Site[7]等以企业的运营成本和乘客的出行成本最小为目标，建立数学模型优化列车车型、发车频率和相对行车间隔；宋瑞等[8]针对城市轨道交通线路运营计划编制传统方法的不足，通过纳入对乘客超乘行为与留乘行为的成本惩罚，建立了运行计划优化模型；凌俊等[9]针对非高峰期城市轨道交通客流不均的现象，建立双目标多约束优化模型，灵活设计列车的运行组织方案.在网络化运行组织优化方面，胡兴丽等[10]通过分析轨道交通在不同运行组织下的通过能力，对相同制式下的轨道交通跨线运行组织进行了优化；王永亮等[11]通过引入备选集的方法建立了双层规划模型，对城市轨道交通网络化列车运行组织方案进行优化.

但是，该领域已有的研究成果大多着眼于各线路独立开行模式，对区域轨道交通与地铁网络跨线运行的运行组织方案研究较少，且相关运行组织优化研究中缺乏针对乘客不同出行需求的考虑.本文作者通过考虑跨线列车对非跨线客流出行的影响和开行跨线列车的行车间隔等条件，基于客流出行分布细化客流类型，建立多目标混合整数非线性优化模型，对承运各类客流的列车行车密度进行优化.

1 模型建立

在列车运行组织方案编制过程中，列车的行车密度是衡量系统运输能力的一个重要指标.因此，通过建立数学模型，对各线路普通列车和跨线列车的行车密度进行优化，使得在满足各交路客流需求、线路运能等条件下，得到成本最小时各交路每小时开行列车的对数.优化过程中，要综合考虑企业和乘客的利益，实现社会效益最大化.

与单线运行时的计算模型相比，开行跨线列车时的计算模型有其自身的特殊性.列车跨入被跨线路的方式不同，会对被跨线路的运能造成不同的影响：当跨线列车通过取代被跨线路列车的方式完成跨线时，会降低非跨线区段的运能；当跨线列车通过插入到被跨线路列车间完成跨线时，会增加跨线区段的运能.跨线列车在输送跨线客流的同时，也会承运部分非跨线客流.因此，各类列车的行车密度需要与不同区段的客流需求特征相匹配，满足各类客流需求.另外，计算模型要充分体现开行跨线列车时的优势，与单线运行模式相比，开行跨线列车要使得跨线客流在更低成本下实现直达，并取得更高的社会效益.

1.1 假设条件

1)列车在各线路上为“站站停”运行模式，且不考虑小交路.

2)不考虑快慢车运行方案，认为同一交路上列车的周转时间是相同的.

3)为了减少对被跨线路中非跨线区段运能的影响，跨线列车进入被跨线路运行时，插入到该线路原有列车之间，不取代该线路上原有的普通列车.

4)认为一定时段内起讫点之间的客流出行量由该起讫点之间的直达列车承担.对于跨线客流，当乘坐跨线列车不能实现直达时，选择乘坐发车密度相对较高的普通列车，经一次换乘后实现过轨，减少候车时间.

5)认为参与跨线运行线路中的设施、设备已预留有跨线运行的实施条件，包括列车过轨设施的预留以及不同线路间车辆、供电、信号等设备的兼容或统一.

6)列车运行组织方案的编制应以客流需求特征为基础，在满足客流需求的前提下，列车的发车间隔受列车服务水平的限制.因此，本文认为在一定的列车服务水平约束下，高峰小时内客流需求量受发车间隔大小的影响较小，为降低模型的复杂度，不考虑客流量与行车间隔间的交互影响.

1.2 目标函数

1)列车运营成本.

列车运营成本可以分为列车运营的固定成本和可变成本.固定成本与列车运用数量有关，可变成本与列车行车密度和运行交路长度有关.假设某线网由n条线路组成，线路i、j为该线网中两条不同的线路. 其中，线路i上的部分列车需要跨线至线路j上运行，则保证列车运营成本最小时的目标函数可以表达为

i≠j，i、j、k=1,2,3,…，n

(1)

式中：a为每列车分摊至单位时间内的购置费用，元/(列·h)；b为每列车运行单位里程时的费用，元/(列·km)；nk为线路k普通列车行车密度，nk≥0且为整数，对/h；ng(i,j)为线路i上的列车跨线至线路j上运行时，该跨线列车的行车密度，ng(i,j)≥0且为整数，对/h；Tkk为线路k普通列车的周转时间，min；Tg(i,j)为线路i上的列车跨线至线路j上运行时，跨线列车的周转时间，min；Lk为线路k交路的长度，m；Lg(i,j)为线路i上的列车跨线至线路j上运行时，跨线交路的长度，m；⎤为向上取整.

2)乘客出行成本.

由于乘客换乘时的走行时间与决策变量(列车的行车密度)无关，可以看作常量不予考虑；一般情况下，各列车通过相同的区间和车站时，通常采用相同的区间通过时间和停站时间.因此，为了降低建模的复杂性，可以认为乘客总的车内时间是固定的[12]，此处不予考虑.因此，对于乘客的出行成本，本模型只考虑候车时间成本.

相关统计数据表明[13]，在行车间隔较短的情况下，乘客的平均候车时间趋近于行车间隔的一半.各类运行模式的列车对于不同出行需求的客流具有不同的适用性.因此，需要根据客流需求分布对客流进行分类，分别计算各类客流总的候车时间.客流总的出行时间成本可表示为

(2)

式中：c为乘客的单位时间价值，元/min；Px为第x类客流总量，人；nx为分担第x类客流的列车行车密度，nx≥0且为整数，对/h.

其中，起点位于Oa站～Ob站之间，终点位于Da站～Db站之间的客流量Px为

(3)

式中：POiDj为以Oi为起点，以Dj为终点的OD客流量，人.

线路i跨线至线路j运行时，分担第x类客流的列车行车密度nx取值见表1.

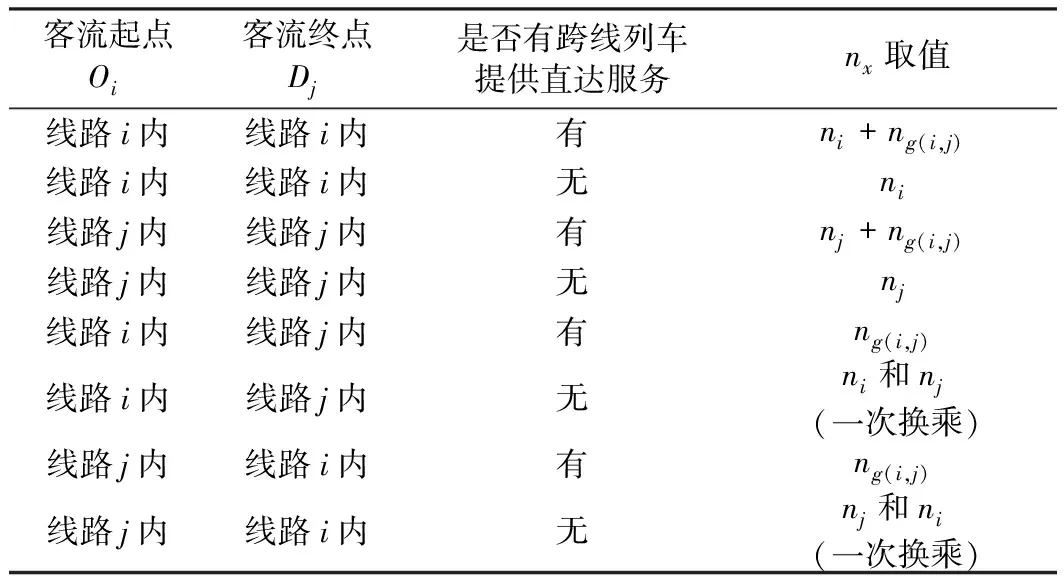
表1 分担不同种类客流的列车行车密度nx取值

1.3 约束条件

1)跨线列车主要解决乘客出行中的直达问题，可以减少跨线乘客的换乘时间，缓解大客流车站的换乘压力，提高出行效率.因此，跨线客流若选择乘坐跨线列车直达目的地，其出行时间成本应该低于乘坐普通列车通过换乘到达目的地的出行方式成本，两种方式消耗的出行时间成本之间应该满足

(4)

由此可推出

(5)

i≠j,i、j=1,2,3，…，n

式中：ti、tj分别为线路i、线路j普通列车的行车间隔，min；tz(i,j)为从线路i通过换乘的方式到达线路j时的平均换乘走行时间，min；tg(i,j)为线路i的列车跨线至线路j上运行时，跨线列车的行车间隔，min；ni、nj分别为线路i、线路j普通列车的行车密度，对/h.

2)开行跨线列车时，不但要使得跨线客流在更低成本条件下实现直达，还要保证企业与乘客的总成本小于各线单线运行时的总成本，满足

(6)

式中：Z1′、Z2′分别为采用单线运行组织方式时企业的运营成本和乘客的出行成本.

其中，对于参与跨线运行的线路，当采用单线运行模式时，各线路行车密度为跨线运行时各线路普通列车行车密度与跨线列车行车密度之和，单线运行时Z1′、Z2′分别满足

b[Li(ni+ng(i,j))+Lj(nj+ng(i,j))]

(7)

(8)

i≠j,i、j=1,2,3，…，n

式中：Pii、Pjj分别为起讫点都在线路i、线路j的客流量；Pij为起点在线路i，讫点在线路j的客流量；Pji为起点在线路j，讫点在线路i的客流量.

3)跨线列车直达范围内的非跨线客流也会占用跨线列车部分载客量，为了满足总的客流需求，各线路上的列车运力要大于上下行最大断面流量.因此，各线路最大断面流量须满足

Pmax，id1≤(niθi+ng(i,j)θg(i,j))·V

(9)

Pmax，id2≤ni·V·θi

(10)

Pmax，jd1≤(njθj+ng(i,j)θg(i,j))·V

(11)

Pmax，jd2≤nj·V·θj

(12)

i≠j,i、j=1,2,3，…，n

式中：Pmax，id1、Pmax，id2分别为线路i上跨线列车直达范围内和非直达范围内上、下行最大断面流量，人；Pmax，jd1、Pmax，jd2分别为线路j上跨线列车直达范围内和非直达范围内上、下行最大断面流量，人；V为列车定员，人/列；θi、θj分别为线路i、j上普通列车的满载率；θg(i,j)为线路i上的列车跨线至线路j上运行时，跨线列车的满载率.

4)跨线列车运力需要满足跨线客流需求，可表达为

Pmax，g(i,j)≤ng(i,j)·V·θg(i,j)，

i≠j,i、j=1,2,3,…，n

(13)

式中：Pmax，g(i,j)为线路i上的列车跨线至线路j上运行时，跨线交路上下行最大跨线客流量，人.

5)若列车内过于拥挤，会降低列车的服务水平，严重影响乘客的舒适性，减少乘客乘坐该线路列车的吸引力.因此，需要保证各交路列车处于一定的服务水平，满足

(14)

(15)

(16)

(17)

式中：θmax，i、θmax，j分别为线路i、j的列车最大满载率限值.

6)各线路开行的列车总数不能超过各线路最大通过能力，表示为

ni+ng(i,j)≤Nmax,i

(18)

nj+ng(i,j)≤Nmax,j

(19)

i≠j,i、j=1,2,3，…,n

式中：Nmax,i、Nmax,j分别为线路i、j的最大通过能力，大于0且为整数，对/h.

2 模型求解

本模型为双目标非线性混合整数优化模型，当列车行车密度增大时，列车运营成本相应增加，但是乘客出行成本会降低.因此，考虑到城市决策者的实际需要，引入权重系数进行线性变换，转化为单目标优化问题.转化后的目标函数为

MinZ=wZ1+(1-w)Z2

(20)

式中：w为权重系数，满足0≤w≤1，作为成本控制的偏好系数，用以表示决策者分别对运营商和乘客利益的重视程度[14-15]，w越大，表示对运营商利益的重视程度越大，对乘客利益的重视程度越小.

由于Lingo软件可以方便、高效地求解单目标非线性混合整数规划问题，软件中采用的顺序线性规划法(SLP法)可有效求解非线性问题，因此,本文利用Lingo软件求解,计算过程不再赘述.

3 算例分析

3.1 计算参数

由于在区域轨道交通网络化运行中，列车运行组织方案的制定是一个庞大的系统工程，本文仅以某市远期规划的一条区域快线跨线至一条普通地铁线路运行为例，优化各交路列车的行车密度.该算例中，SL1={S1,S2,…，S21}为一条区域线路的车站集合，该线路主要承运城市外围组团与城区间的通勤客流；SL2={S1′,S2′,S3′,…，S32′,S20}为一条普通地铁线路的车站集合，其中，S3′站位于大型客运枢纽内，S20为换乘车站，同时预留有实施跨线运行的条件.为实现外围组团客流能够直达市内客运枢纽，同时减少车站S20的换乘压力，将S1-S3′-S1作为跨线交路，各交路方案见图1.

模型中各参数的取值见表2，根据早高峰小时站间OD客流数据，计算得到的不同种类客流及分担各类客流的列车行车密度见表3.

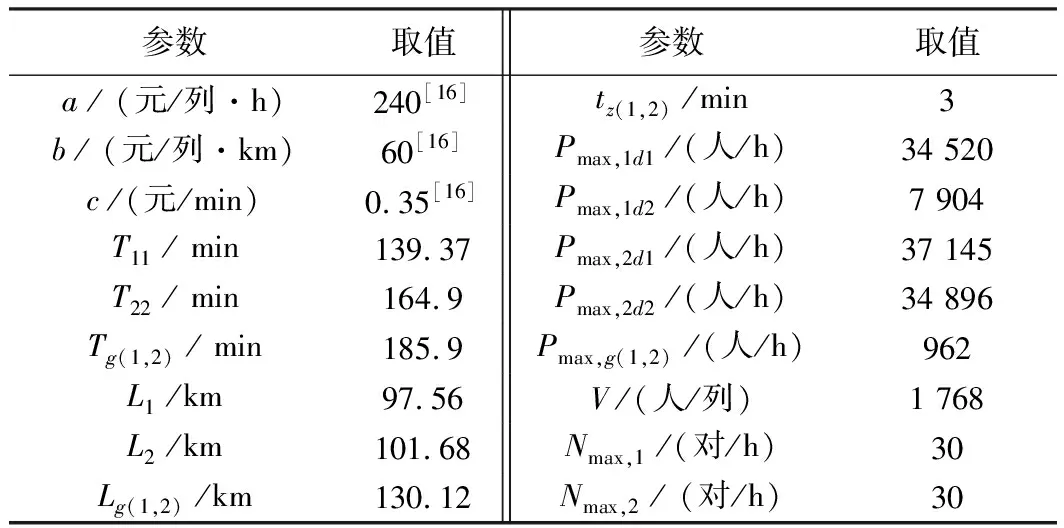
表2 模型中各参数的取值

3.2 求解结果

为了控制车厢内乘客的拥挤程度，并满足列车运能的要求，将各线路列车最大载客量分别限制为定员载荷(θmax=θ1max=θ2max=1)和超员载荷(3 110人/列，此时θmax=θ1max=θ2max=1.76).当w取不同的值时，各变量的优化结果见表4、表5，各成

表3 各类客流及分担各类客流列车的行车密度

本随w的变化曲线见图2、图3.

由表4、表5和图2可以看出，随着对运营商利益重视程度的增大，总体上各线路普通列车行车密度逐渐降低，从而造成列车运营成本逐渐降低，乘客的出行成本逐渐增加.若列车最大载客量限制为定

表4 θmax=1时各变量的优化结果

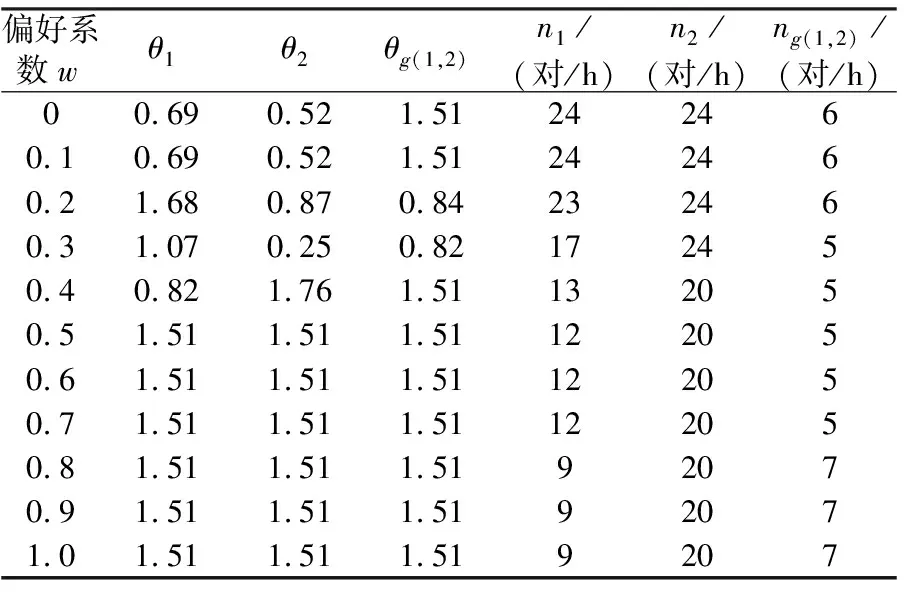
表5 θmax=1.76时各变量的优化结果

员载荷，偏好系数范围为0.4≤w≤1时，运营成本与乘客出行成本达到平衡，此时总成本降到最小，为434 842.70元，列车开行优化结果为：各线路列车最优满载率取值范围分别为0.98≤θ1≤1.00，0.90≤θ2≤1.00，0.99≤θg(1,2)≤1.00；最优行车密度n1=15对/h，n2=20对/h，ng(1,2)=5对/h.若列车最大载客量限制为超员载荷，偏好系数取0.5≤w≤0.7时，运营成本与乘客出行成本达到平衡，此时总成本降到最低，为428 354.20元，列车开行的优化结果为：各线路列车最优满载率为θ1=θ2=θg(1,2)=1.51；最优行车密度为n1=12对/h，n2=20对/h，ng(1,2)=5对/h.

若不采用跨线运行的方案，且各线路均采用与跨线运行时相同的行车密度时，其成本与跨线运行时的成本之差与w之间的关系见图3.由图3可以看出，各线路单线运行时，乘客的出行成本差为负值，企业运营成本差为正值，说明采用单线运行时乘客总的出行成本有所降低，企业运营成本有所增加.随着对企业运营成本重视程度的增加，单线运行与跨线运行之间的总成本之差逐渐降低，说明此时开行跨线列车的优势逐渐降低.因此，当开行跨线列车时，不能因过于重视运营成本而忽视乘客出行的成本效益.

4 结论

1)针对区域轨道交通线路与地铁线路之间的跨线运行组织模式，建立了区域轨道交通跨线运行模式下多目标混合整数非线性优化模型.模型中考虑了企业与乘客的成本效益、开行跨线列车时的行车间隔条件、列车的服务水平、以及跨线列车在其直达范围内对非跨线客流的承运作用等，并通过引入偏好系数控制对企业效益和乘客利益之间的重视程度.基于客流需求分布细化客流类型，在满足客流量需求、保证一定的列车服务水平的前提下，对承运各类型客流需求的列车进行行车密度优化.

2)以某市规划的一条跨线线路运行为例，基于该模型计算得到了各类型列车的最优行车密度，验证了模型的适用性和合理性.通过计算，得到了企业和乘客效益平衡时的偏好系数，同时优化得到了一定服务水平下偏好系数控制的列车最佳满载率.