多孔介质热流耦合传热模拟研究

吴贵福 杨印章 刘仁强 王志国 贾天骄 刘立君

摘      要： 針对稠油热采过程中高温高压流体注入油藏多孔介质引起的温度场和速度场的变化情况，以达西定律为基础，采用有限体积法建立多孔介质热流耦合方程。基于REV尺度多孔介质模型进行模拟计算，研究多孔介质的渗透率和体积分数，以及热采过程中热流体的注入压力，对多孔介质内热流耦合传热过程的影响。结果表明：增加渗透率对多孔介质传热的效果优于增加入口压力，固体体积分数增大，增加热阻，导致传热效果降低。增大注入热流体压力，能够增加热量传递速度。

关  键  词：数值模拟;热流耦合;渗透率;体积分数

中图分类号：TE345       文献标识码： A       文章编号： 1671-0460（2020）03-0697-05

Simulation Study on Heat Flow Coupled Heat Transfer in Porous Media

WU Gui-fu¹， YANG Yin-zhang²， LIU Ren-qiang³， WANG Zhi-guo²， JIA Tian-jiao²， LIU Li-jun^2*

（1. College of Mechanical Engineering， Jiamusi University， Heilongjiang Jiamusi 154000， China;

2. College of Civil Engineering， Northeast Petroleum University， Heilongjiang Daqing 163000， China;

3. Exploration and Development Research Institute of Daqing Oilfield Limtied Company， Heilongjiang Daqing 163712， China）

Abstract： Aiming at the changes of temperature field and velocity field caused by high temperature and high pressure fluid injected into reservoir porous medium during heavy oil thermal recovery process， based on Darcy's law， the coupled equation of heat flow in porous media was established by the finite volume method. Based on the REV-scale porous media model， the effect of permeability and volume fraction of porous media and the injection pressure of hot fluid during thermal recovery on the heat flow coupling heat transfer process in porous media was studied. The results showed that the effect of increasing the permeability on the heat transfer of porous media was better than increasing the inlet pressure， increasing the solid volume fraction and increasing the thermal resistance， resulting in a decrease in heat transfer. Increasing the pressure of the injected hot fluid could increase the heat transfer rate.

Key words：  numerical simulation;  heat flow coupling;  permeability;  volume fraction

能源、环境和可持续发展是21世纪人类社会生存和发展的主题，三者之中可持续发展是中心，能源与环境是保障和基础^[1]。稠油资源，一般来说具有高黏度、高凝点和胶质与沥青含量高（三高）等特点，常规方法较难采出。热力开采方法是目前国内外开采稠油资源的有效方法之一^[2，3]。油藏区域属于多孔介质结构，多孔介质内部孔隙分布不均匀，使得其内部流动非常复杂。由于流动形态及流动方式不断变化，对多孔介质内部热流耦合传热效果影响很大。目前对多孔介质传热特性有较广泛的研究，采用实验和建立理论模型进行有限元分析的方法。

实验研究方面，付超^[4]等通过底部热加载的方式对两层多孔介质热流耦合对流传热特性进行研究。张云嵩等^[5]研究射流冲击条件下多孔介质覆盖的流动液膜的传热特性。李刚等^[6]以纳米流体为流动介质填充到充满玻璃球的等腰三角形多孔介质腔体，研究不同顶角的自然对流换热。通过实验的方法对多孔介质进行研究可以得到实际情况下多孔介质流动的传热特性，但是实验方法对实验设备和实验原料要求高，而且偶然性事件发生容易误导实验人员，导致实验的结果出现非常规现象，进而影响我们对变化情况的分析。数值模拟从已知的物理定律出发，通过求解基本定律在特定物理条件下的数量关系，并总结出结论。数值模拟方法可以实现反复运算，能够方便地控制和调整参数。

利用数值方法，Fetzer等^[7]对土壤蒸发过程进行简化和参数化，建立了两组数值模拟，研究表明均质和非均质多孔介质对蒸发传热具有重要性，并且土壤中的侧向热量流动对蒸发传热起着重要作用。Khan等^[8]利用非线性常微分方程，研究了多孔介质中的渗透表面，并在对其进行热力学分析，得到了无量纲速度、温度、表面摩擦系数和局部努塞尔数的解。刘佳琪^[9]运用CFD方法对天然气水合物注蒸汽开采过程进行数值模拟，对注蒸汽温度、注蒸汽速率和孔隙度等影响因素进行研究。张一凡^[10]基于容积平均和局部热平衡法，研究多孔介质壁面对槽道湍流流动及传热的影响，对含有多孔介质壁面槽道湍流的流场和温度场进行直接数值模拟。冯守玲^[11]以微小反应器固定床为研究对象，采用fluent数值模拟软件分析固定床内树脂颗粒的传热特性。王强^[12]利用fluent数值分析软件模拟指尖密封结构内的流动与传热特性。任浩^[13]等人通过数值模拟的方法，研究蒸汽驱对油藏采收率的影响，并对剩余油分布进行分析。

从国内外研究现状中可以看出，大多数研究者对多孔介质传热特性都是从多孔介质自身的属性上对多孔介质进行研究，但是外部条件对多孔介质传热的影響研究较少。本文从外部条件和自身属性条件对多孔介质传热特性进行研究，建立了均匀多孔介质二维简化几何结构模型，对多孔介质内部的热流耦合过程进行数值模拟，并分析渗透率、体积分数和热采过程中的入口压力对传热过程的影响。开展本研究，可以深入研究驱油过程中的一些基础和难点问题，实现科技增油、缓解我国油气供需矛盾和保障石油安全提供理论基础。

1  计算模型

油藏多孔介质内部的换热方式主要包括油藏多孔介质骨架自身的导热和油藏多孔介质内部流体的导热与对流。为便于研究油藏多孔介质热流耦合传热的影响，本文计算忽略内部气体的导热与对流以及辐射换热，只考虑多孔介质内部流体与固体之间的热流耦合过程。

模型建立过程基于以下简化假设：（1）岩石骨架和原油为不可压缩;（2）整个过程为瞬态过程，考虑温度的瞬态影响;（3）渗流过程为单向流体;（4）多孔介质渗流服从达西定律;（5）多孔介质区域为各向同性;（6）流体为单相流体。

1.1  油藏多孔介质的运动过程

（1）运动方程

多孔介质传质过程符合达西渗透定律，达西定律渗流方程为：

（1）

式中：V₁ — 达西渗透速度，m/s;

κ — 多孔介质渗透率;

μ —流体的动力黏度，Pa·s;

P — 压力梯度，MPa。

（2）连续性方程

在不考虑源、汇的情况下，流体和固体的连续性方程为：

         （2）

式中：t — 时间，s;

ε_s — 多孔介质孔隙度;

ρ₁ — 流体密度，kg/m³。

将运动方程代入连续性方程，然后整理得到的渗流微分方程为

（3）

1.2  油藏多孔介质的传热过程

多孔介质内部传热过程采用二维非稳态导热微分方程，二维非稳态导热微分方程为

        （4）

根据有效体积法，确定多孔介质的有效体热容，有效体热容方程如下

    （5）

式中：（ρC_P）_eff — 有效体热容，J/（kg·K）;

ρ_s — 多孔介质骨架密度，kg/m³;

θ_s — 多孔介质的体积分数;

C_s — 多孔介质骨架恒压热容，J/（kg·K）;

C_l — 流体恒压热容，J/（kg·K）。

根据有效体积法求得模型的有效导热系数，有效导热系数方程为

        （6）

式中：k_eff— 有效导热系数，W/（m·K）;

k_s— 骨架的导热系数，W/（m·K）;

k_l — 流体的导热系数，W/（m·K）。

多孔介质内热流密度方程如下，式中负号表示热量传递方向与温度升高的方向相反。

            （7）

式中：q — 热流密度，W·m^-2;

d_z — 厚度，m;

T — 温度梯度，K。

能量守恒方程

     （8）

將上述方程代入能量守恒方程，得到多孔介质能量守恒方程

    （9）

2  数值模拟方案

岩石多孔介质特性一般通过体积分数、渗透率等特征系数表示。体积分数越大，表示单位体积的多孔介质中有更多的骨架基体，孔隙所占体积较少;渗透率越大，表示流体在多孔介质中的渗透能力越大。

本文针对油藏多孔介质，开展基于REV尺度的油藏多孔介质，进行热流耦合计算，得到多孔介质流动特性与传热特性。油藏多孔介质内部的孔隙是无规律分布，直接建立与实际完全相同的模型非常困难，因此本文将计算模型简化为REV尺度的宏观模型。并进行了网格无关性验证。

在网格尺寸独立性的研究部分，模拟计算网格数为5 944， 5 860和2 836的模型，对比不同网格数量下出口温度随时间变化的情况，如图1（a）所示。

在网格数量5 944和5 860下温度随时间变化的曲线相对接近，网格数为5 860下模拟的精度已经达到最优值，继续增加网格数量对于计算精度的提高作用不大，而且还会增加模拟的计算量，为了能更加有效地完成研究，选择网格数量为5 860。在选择时间步长的研究中，分别模拟了1，10和50 h，从图1（b）可以发现1和10 h的曲线几乎重叠，可以认为时间步长为10 h的情况下，模拟已经达到最佳值，为了得到更加详细的数据结果，所以选择时间步长为1 h。

模型的长度L= 71.5 cm，高度H= 91 cm，初始压力P₀= 5 MPa，初始温度T₀= 372.15 K，入口温度T_in=473.15 K。多孔介质固体的密度为2.4×10⁶kg/m³，恒压热容为833.3 J/（kg·K），导热系数为1.85 W/（m·K），孔隙率为0.3。多孔介质流体的恒压热容为2 100 J/（kg·K），导热系数为0.15 W/（m·K）（图2） 。

流体密度采用文献^[14]中使用的密度函数：

（10）

式中：ρ— 流体密度，W·m^-2;

T— 温度，K。

3  模拟结果及分析

图3为模拟结果的速度场云图和速度矢量图，从图3中可以看出，沿着入口方向上，速度矢量分布较为密集，而两侧的较为稀疏，这是因为沿压力入口方向上，压力梯度变化大于两侧的压力梯度变化，导致速度增大。图4为多孔介质孔喉处的速度矢量图，从图4中可以看出，在孔喉处，随着孔喉尺度的减小，流体流过的通道变得狭窄，导致流体的速度变大，在孔喉最小的尺寸处得到流速最大值。

图5为多孔介质传热过程中不同时刻的温度变化情况，从图5可以看出，沿着压力入口方向上的温度传递速度大于压力入口两侧的温度传递速度，这是由于模型中部的流体流动速度大于两侧的流体流动速度。为了研究其传热规律，选取模型出口温度作为研究对象，探究入口压力、渗透率和体积分数对温度传递的影响。

3.1  油藏渗透率对温度传递的影响

渗透率对温度传递存在很大的影响，分别模拟计算对比渗透率k= 15、150、500和2 000 mD时温度变化情况，结果如图6和图7所示。

从图6中可以看出，随着油藏多孔介质渗透率的增大，出口温度达到稳定的时间变得的越短，说明油藏温度传播的速度加快。造成这种结果的原因是：当多孔介质渗透率增大时，多孔介质内部的流体热传导能力加强。多孔介质传热主要的方式为导热和对流传热，其中内部流体传导能力加强，使得流体与固体之间的对流传热加强，影响整个区域的传热过程。

从上面的分析中可以看出，多孔介质渗透率对多孔介质的传热过程影响很大，不能仅通过渗透率来预测传热过程的变化规律，还应该考虑孔隙度和孔隙几何结构对传热过程的影响。

3.2  多孔介质体积分数对多孔介质传热的影响

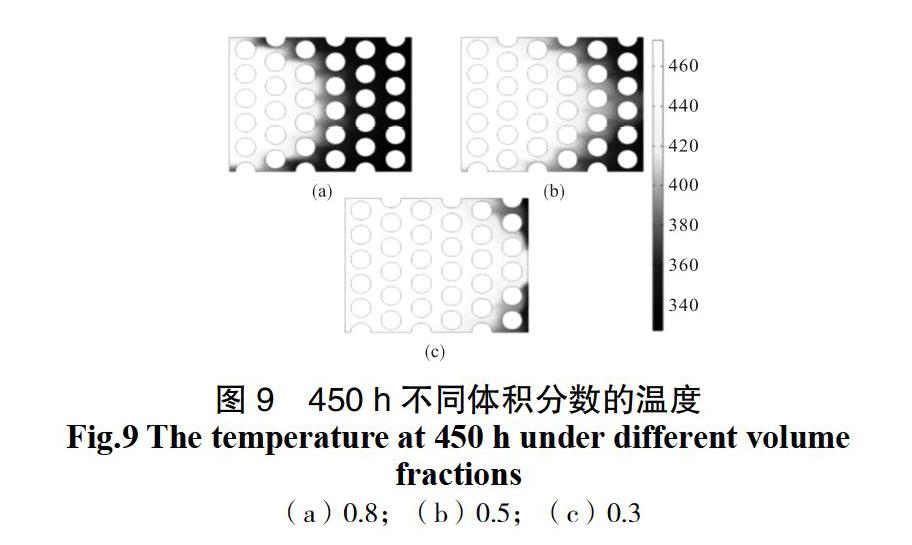
作为描述多孔介质的特征主要参数，体积分数是影响多孔介质传热特性的重要因素。由多孔介质体积分数定义可知，体积分数越大，单位体积内固体所占得体积较大。固体与流体的恒压热容与导热系数相差较大，所以多孔介质体积分数对温度传递存在较大的影响，本文分别模拟体积分数为0.3、0.5和0.8时多孔介质传热的变化情况，结果如图8和图9所示。

从图8中可以看出，体积分数越大出口温度升高地越慢，体积分数越小，温度升高的非线性增大越明显。这是由于相同条件下，体积分数越大，固体所占的体积增大，虽然强化了固体导热，但是固体的导热熱阻比流体的导热热阻大，并且内部流体的体积减小，降低了对流传热作用，使得流体在内部传热效果降低。随着体积分数的增加，油藏多孔介质骨架截面界面变小，降低了流体通过多孔介质的流动能力。通过上面的分析可以看出，多孔介质的渗透率和体积分数都影响到了多孔介质的传热情况。

3.3  入口压力对温度传递的影响

除了多孔介质本身的属性影响传热外，由于入口压力导致的压力场的变化，也会引起传热效果的改变。为了研究热采过程中入口压力对温度传播的影响，分别计算对比了压力P=6、8a和10 MPa时温度变化情况，结果如图10和图11所示。

从图10中看出，随着入口压力的增大，出口温度变化的速率也随之增大，增大呈明显非线性增大。根据达西定律，流体在多孔介质中的流动速度与压力梯度呈线性关系，压力梯度增加导致流体流动速度也相应地增加，速度增大强化了对流传热，最终导致传热速率增加。

渗透率与流体入口压力对多孔介质热流耦合传热影响的根本原因都是通过增加流体在多孔介质中的流动速度，使得多孔介质内部的对流传热加强。将图6与图10进行比较，可以明显看出增加渗透率对多孔介质传热的效果优于增加入口压力，所以如何通过技术手段增加油藏多孔介质的渗透率，是一个亟待解决的问题。

4  结论

本研究考虑多孔介质中流体流动与温度耦合传热过程，对多孔介质的渗透率、体积分数和热采过程中的入口压力对传热的影响进行了数值分析，主要得到以下结论：

（1）均匀多孔介质在渗透率较高的情况下，多孔介质传热的速度加快，这是由于渗透率影响渗透速度，从而使对流传热的强度增加，但是对于多孔介质结构，不能仅以渗透率来判断多孔介质传热，还需要从多孔介质的几何结构和孔隙率等方面研究多孔介质传热。

（2）由于多孔介质结构的特殊性，主要存在导热和对流换热，所以，固体与流体的体积分数对多孔介质传热尤其重要，当体积分数越大，固体所占得体积增加，单位体积内流体减少，整体热阻增加，使得传热速度降低。

（3）增大热采流体的注入压力，能有效提高流体在多孔介质中的渗流速度，从而增加流体在多孔介质中的对流传热效果。

参考文献：

[1]马一太，吕灿仁. 能源利用可持续发展的热力学分析[J]. 热科学和技术，2004， 3（1） ：86-90

[2] 李景宝. 提高稠油开采的技术研究[J]. 中国科技信息， 2009，（03）：18-19.

[3]张义堂，等.热力采油提高采收率技术[M].北京：石油工业出版社， 2006.

[4]付超， 王赫宇， 杨伟，等. 底部热加载下两层多孔介质热流耦合现象研究[J]. 应用力学学报， 2017， 34（3）：489-494.

[5]张云嵩， 陈威， 程建，等. 射流冲击泡沫金属流动液膜传热的实验研究[J]. 低温与超导， 2018（2）.

[6]李刚， 张策， 张尧，等. 多孔介质等腰三角形腔体内自然对流换热[J]. 甘肃科学学报， 2018（1）：85-89.

[7] Fetzer T ， Vanderborght J ， Mosthaf K ， et al. Heat and water transport in soils and across the soil-atmosphere interface： 2. Numerical analysis[J]. Water Resources Research， 2017， 53（2）：1080-1100.

[8] Khan Z H ， Qasim M ， Haq R U ， et al. Closed form dual nature solutions of fluid flow and heat transfer over a stretching/shrinking sheet in a porous medium[J]. Chinese Journal of Physics， 2017， 55（4）： 1284-1293.

[9]劉佳琪， 刘宝玉， 赵华. 天然气水合物注蒸汽开采影响因素研究[J]. 石油和化工节能， 2017（5）：33-41.

[10]张一凡， 刘财喜， 董宇红. 多孔壁面槽道湍流中的流动阻力和传热[J]. 上海大学学报：自然科学版， 2018， 24（3）.

[11]冯守玲， 郑艺华， 张心怡，等. 多孔材料固定床内温度场的数值模拟研究[J]. 青岛大学学报（工程技术版）， 2017， 32（2）：91-95.

[12]王强， 胡娅萍， 吉洪湖. 基于多孔介质的指尖密封各向异性传热模型[J]. 航空动力学报， 2017， 32（11）：2585-2595.

[13]任浩， 刘永建， 姚帄旗， 等. 齐40块高倾角油藏蒸汽驱后期剩余油分布研究[J]. 当代化工， 2019（7）：1615-1618.

[14]Xu Ying，Nie Xin，Cheng Qinglin，Dai Zhonghua，Liu Xiaoyan，Liu Yang， L. I. Cong. Phase-change heat transfer analysis of shutdown overhead pipeline[J]. Case Studies in Thermal Engineering，2019，13.