一种基于化学势LBM多相流模型的改进方法

2020-04-07,,,

广西师范大学学报（自然科学版） 2020年2期

,,,

(广西师范大学广西多源信息挖掘与安全重点实验室，广西桂林541004)

晶格Boltzmann方法(lattice Boltzmann method，LBM)由于物理背景清晰，算法简单，计算效率高和适合大规模并行计算等诸多优点，已在多相流领域得到众多学者们的关注和应用[1-5]。目前，比较流行的LBM多相流模型主要有：①1991年，Gunstensen等[6]提出的颜色梯度模型；②1993年，Shan等[7]提出的直接刻画粒子间相互作用的伪势模型；③1995年，Swift等[8-9]基于自由能理论提出的自由能模型。其中伪势模型和自由能模型应用最为广泛。

伪势模型，又叫Shan-Chen模型，是通过一种假设的相互作用势来刻画流体微观粒子之间的相互作用。该模型虽然算法简单且容易捕获和跟踪相界面，但也有一些局限性：一是只有当有效密度满足φ(x)=φ0exp(-ρ/ρ0)(其中ρ表示密度，ρ0和φ0表示参考密度和质量)时，该模型才符合热力学一致性。但在实际应用中，往往有效密度并不取这一特殊形式；二是只适用于密度比较小的多相流系统；三是当模拟达到平衡时，相界面处存在较大的虚速度。多年来，众多学者对其进行了研究和改进：2003年，Zhang等[10]采用势函数的形式计算粒子间的相互作用力，使得伪势模型的稳定性得以提高；2006年，Yuan等[11]通过将各类状态方程引入模型，扩展了原始伪势模型的应用范围，实现了更高的密度比，但却依然存在热力学不一致的缺点；2009年，Kupershtokh等[12-13]采用折合变量的思想，提出了一种以加权的方式将有效密度形式和势函数形式结合起来计算粒子之间的相互作用的模型，当取合适的权值时，模型的稳定性得到大大提高；2013年，Hu等[14]通过在状态方程前添加一个可调的参数，能够很好地提高模拟的稳定性；2018年，Qin等[15]引入高阶差分来计算非理想流体的相互作用势，有效地提高了模型的精确度，使得计算结果更加可靠。

基于热力学自由能理论，1995年，Swift等[8-9]将压力张量耦合到平衡分布函数，提出了自由能模型。虽然在理论上具有热力学一致性，但是原始的自由能模型并不满足伽利略不变性这一物理基本规律[9，16]，构建的新平衡态分布函数也较为复杂。针对这些问题，2000年，Inamuro等[16]通过调节平衡态分布函数中各项系数的方式来减少模型不具有伽利略不变性所带来的影响；2015年，Wen等[17]通过分析伪势模型和自由能模型各自的缺陷和特点，将基于热力学计算得到的非理想力通过伪势模型的力项技术合并到晶格Boltzmann方程中，提出了同时满足热力学一致性和伽利略不变性的多相流模型；2017年，Wen等[18-19]又从化学势(chemical potential，CP)的角度考虑，构建了一种基于化学势的晶格Boltzmann方法多相流模型，该模型相比于基于压力张量的模型[17]避免了计算具有各向异性的压力张量及其散度，只需要计算化学势的梯度，从而大大提高了计算效率和模型的稳定性。

值得注意的是，在Kupershtokh等[12-13]的工作中，通过引入折合变量pr=p/pc,ρr=ρ/ρc,Tr=T/Tc，式中p表示压强，ρ表示密度，T表示温度，pc、ρc、Tc分别表示临界压强、临界密度和临界温度，pr、ρr、Tr分别表示折合压强、折合密度和折合温度，对van der Waals状态方程(VDW EOS)进行了重新定义，发现基于折合变量的状态方程相比原方程没有任何与具体物质相关的参数，因此可以定性地描述真实流体的相关特性，使得方程更具有普适性。

受到以上工作的启发，本文拟将折合变量引入到化学势多相流模型中，构建一种基于折合的化学势LBM多相流模型，并对该模型在性能和实用性上进行数值模拟验证。

1 改进化学势模型

1.1 化学势LBM多相流模型

在非理想流体系统中，含有梯度平方近似的自由能泛函可以表示为[9,17,20]：

(1)

其中积分第一项是自由能密度函数，第二项是密度梯度对自由能的贡献，κ是与界面厚度和表面张力有关的系数。化学势由自由能密度函数决定：

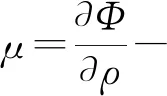
(2)

其中,

(3)

由方程(2)和(3)可得：

μ=ψ′(ρ)-κ2ρ。

(4)

对于各类流体系统，其状态方程的通用形式为：

p0=ρψ′(ρ)-ψ(ρ)。

(5)

系统的非理想力可以由化学势求得[18]，即

F(x)=-ρμ+

(6)

另外，本文使用标准单驰豫晶格Boltzmann演化方程：

(7)

(8)

其中ωi表示权重系数。在不同的离散速度集模型DnQm(D表示维度，Q表示离散速度，n表示空间维度数，m表示离散速度数)中，ωi、cs与ei的取值是不一样的，下面给出本文使用的D2Q9离散速度模型的相关参数：

(9)

(10)

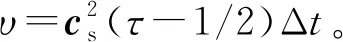
在D2Q9模型下，流体的宏观密度和宏观速度可由分布函数求得：

(11)

(12)

平衡状态下，方程(11)和(12)则是系统质量守恒和动量守恒的基本条件。

本文采用Shan-Doolen力项模型，通过修正平衡分布函数中的速度，将非理想力耦合到LBM演化方程中[21]。非理想力对碰撞过程的影响使得平衡态粒子的动量增加为

ρueq=ρu+τF。

(13)

(14)

1.2 折合表示的化学势

根据方程(5)可以求得自由能密度与状态方程之间的关系：

(15)

其中，C表示积分的常数项。因此，由方程(4)和(13)可知，只要给定状态方程的形式，即可求得各类流体对应的化学势。

以van der Waals流体为例，其状态方程和对应化学势的形式为：

(16)

(17)

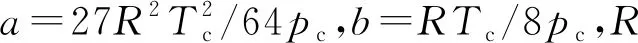
引入折合变量(以下折合后的变量下标均标注为r)：

(18)

则得到折合后的状态方程：

(18)

可以看出，相比原方程，折合状态方程的形式更加简洁，并且与参数a、b无关，避免了与具体物质有关的参数影响。因为折合后的方程是无量纲的，所以此形式下的状态方程更具有普适性[12]。

在格子单位下，以格子时间Δt和格子步长Δx为特征量，将化学势进行折合，得到折合化学势：

由图1可知，卤汁1在复卤过程中总酸含量总体上比卤汁2要高，卤汁1复卤过程中总酸最低含量为0.91 g/kg，最高含量为3.88 g/kg；卤汁2复卤过程中总酸最低含量为1.13 g/kg，最高含量为3.79 g/kg。卤汁中总酸变化的原因可能是，在豆干卤制过程中，工厂每天要进行补料和补水，所以总酸会在一定的范围内波动。卤汁1在卤制过程中，总酸含量在2.71 g/kg上下波动；卤汁2在卤制过程中，总酸含量在2.31 g/kg上下波动。而变化不大的原因是工厂每天会对卤汁总酸进行监控。所以总酸只在一定的范围内波动[9]。

(19)

则van der Waals流体对应的折合表示的化学势为：

(20)

引入折合表示的流体速度和粒子分布函数：

(21)

相应地，折合表示的晶格Boltzmann演化方程变为：

(22)

平衡态分布函数变为：

(23)

(24)

(25)

这里给出折合表示的计算非理想力的分量形式：

(26)

力项模型依然采用Shan-Doolen的平衡态速度修正模型[21]，折合形式下平衡态速度和流体宏观速度被重新定义为：

(27)

2 模型验证

2.1 两相共存密度

在气液相变的数值模拟中，Maxwell等面积重构方法解出的两相共存密度被广泛作为验证模型热力学一致性的基准数据。将计算域划分为100×200的长方形均匀网格流场，流场中部为液体，其余部分为气体，气液两相界面设为水平的，四周采用周期性边界条件，初始流体速度为零，为方便与原化学势多相流模型作对比，根据文献[18-19]，设弛豫时间τ=1.3，参数κ=0.01。

图1 两相共存密度曲线与Maxwell方法理论解的比较Fig.1 Comparison of two-phase coexistence density curves and theoretical solution of Maxwell’s method

为了能够体现改进模型的扩展性，我们同时对VDW EOS、Carnahan-Starling状态方程(CS EOS)、Redlich-Kwong状态方程(RK EOS)、Peng-Robinson状态方程(PR EOS)进行了模拟，并与Maxwell方法理论结果进行比较。如图1所示，在不同状态方程下，当前模型的数值计算结果与Maxwell方法的理论结果都能很好地吻合，这说明当前模型是符合热力学一致性的。我们也对不同状态方程模拟的温度范围进行了考察，如表1所示，与原始化学势模型相比，使用当前模型模拟的温度更低，温度范围更广，这说明当前模型具有很好的稳定性。此外，使用当前模型显著提高了模拟的两相密度比，例如使用PR EOS和RK EOS能够模拟的最低折合温度都为0.34，最大两相密度比分别为3.07×108和5.10×108，均超过了108。

2.2 Laplace定律验证

Laplace定律通常用来评价多相流系统中表面张力的影响，也是验证多相流模型可行性的重要依据。根据Laplace定律，当液滴与周围气体达到稳定状态时，液滴内外压差ΔP与液滴半径R满足：

ΔP=Pin-Pout=σ/R，

(28)

其中，σ表示液滴的表面张力,Pin和Pout分别表示液滴的内部压强和外部压强。

表1 采用原始化学势模型与当前模型能够模拟的温度范围和最大两相密度比

由方程(28)可知，液滴内外压差ΔP与半径R存在线性关系，也就是说要想判断模型是否符合Laplace定律，只需考察ΔP与R的倒数是否成一次函数关系即可。选取VDW EOS进行模拟，在网格大小为256×256的流场中央设置一个静止液滴，四周采用周期性边界条件，弛豫时间τ=1.3，参数κ=0.01。考察折合温度Tr分别为0.6、0.7、0.8时，半径分别为30、35、40、45、50、55、60(格子单位)的液滴内外压差与半径之间的关系，液滴周围为当前温度下饱和的气体。如图2所示，在不同温度下静止液滴内外压差ΔP随半径R的倒数的增加而线性增加，并且两者成正比关系，此结果与Laplace定律相一致。这里每条线都有一个稳定的斜率，代表在当前温度下表面张力的大小。由此验证了当前模型满足Laplace定律。

图2 VDW流体在不同温度下ΔP与1/R的关系Fig.2 Relationship between ΔP and 1/R of VDW fluid at different temperatures

2.3 降低计算中的虚速度

在使用LBM多相流模型进行模拟时，虚速度是衡量模型性能的一个重要指标。如果虚速度过大，则模拟中很难将其与真实流体速度区分开，使得计算结果失去意义。有效降低虚速度的影响一直是多相流领域研究的热门话题。为方便比较，我们仍然以VDW EOS为例，计算区域设置为256×256大小的均匀网格，弛豫时间τ=1.3，κ=0.01，网格中央设置一个静止液滴，液滴周围为当前温度下饱和的气体，四周采用周期性边界条件。考察当折合温度Tr分别为0.82和0.92时，不同半径液滴两相界面处虚速度的大小。

如图3所示，当Tr分别等于0.82和0.92时，当前模型的虚速度都明显低于原始化学势(CP)模型的，由此可以说明使用当前模型可以有效降低虚速度对流体行为的影响。

图3 原始化学势(CP)模型与VDW EOS的虚速度比较Fig.3 Comparing the spurious current of the original chemical-potential(CP) model and the present model

3 模型应用：液滴撞击液膜

作为模型的测试案例和初步应用，我们模拟了单液滴在无重力影响的情况下，以一定初始速度撞击液膜的过程。同样选取VDW EOS，在网格区域大小为2 000×600的二维平面内设置一个液滴，计算域的底部铺展一层液膜，高度为整个计算域高度的1/12，液滴半径R=100，折合温度Tr=0.6，弛豫时间τ=1.25，参数κ=0.01，流场上下边界采用半程反弹边界条件，左右边界采用周期性边界条件。在液滴撞击液膜的过程中，雷诺数Re具有至关重要的作用[22-23]，通常Re=UD/νl，其中U为液滴撞击液膜的初始速度，D为液滴的直径，νl为液体的粘性。