基于有限元法的耐张线夹钢锚工艺缺陷影响分析

李建斌，张一，周浩正，黄金威

(1. 广东电网有限责任公司中山供电局，广东 中山 528400；2. 广东电网有限责任公司湛江供电局，广东 湛江 524000)

耐张线夹是用于固定导线或避雷线至绝缘子串或杆塔，起耐张作用的重要连接金具。在结构上，压缩型耐张线夹主要分为铝管和钢锚2部分,其中铝管用于压接导线或避雷线，而钢锚的挂环通过紧固件连接在非直线杆塔的耐张绝缘子串上，承受导线全部的张力[1-6]。在整个输电网络的安全和稳定运行中，耐张线夹起到重要作用。

在输电网络中耐张线夹普遍存在断裂或脱落现象，这些事故的发生会严重影响电力系统的安全稳定运行，不仅会给电网带来重大经济损失，同时降低电力系统稳定性，目前已有诸多学者对电力系统中出现的耐张线夹断裂事故进行了分析研究。文献[7]对断裂试样进行了化学成分检验和结构解剖，分析得出钢锚碳含量偏高是导致断裂的主要原因；文献[8-9]对断裂试样进行金相检查以及扫描电镜分析，分析得出金属疲劳与线夹空腔积水发生锈蚀是线夹断裂的主要原因；KARABAY S等人[10]研究了钢芯铝绞线由于制造缺陷导致早期失效的原因，但没有分析耐张线夹位置断裂的原因；文献[11-14]中对射线无损在线检测耐张线夹进行了深入研究；文献[15]利用射线检测装置进行了实地勘测任务；亦有学者从耐张线夹的引流作用进行了仿真分析[16-17]，重点分析了电流热效应对线夹性能的影响；AUFAURE M[18]提出了三节点模型，推导出切线刚度矩阵来计算架空输电导线在平衡情况下的水平张力分布，该方法可以利用较少的迭代计算得到稳定解，并且结果可用于导线的载荷计算。

目前文献大都对已发生事故线夹进行事后分析，对于耐张线夹本体缺陷造成的潜在隐患目前还较少进行相关研究。经现场实际测量某批220 kV输电线路所用耐张线夹，发现钢锚凹槽部分由于制造工艺问题导致凹槽深度不一，可能会影响线夹的使用性能和使用寿命，在满足安装工艺要求情况下，有必要对此进行深入探讨。

本文以典型的液压型耐张线夹作为研究对象，进行了选型并简化凹槽和铝管压接部分。首先介绍了耐张线夹的选型及自身的物性参数；其次根据标准技术图纸建立了标准尺寸下的线夹钢锚三维模型，通过分析钢锚所处系统环境得到仿真的边界条件，借助Calculix分析工具对线夹进行了力学仿真分析；对于现场抽样测量耐张线夹钢锚凹槽深度发现存在的制造工艺缺陷问题，本文在标准模型的基础上建立了不同凹槽深度的模型；最后分析了耐张线夹力学仿真结果，同时讨论了耐张线夹钢锚工艺缺陷对线夹使用性能的影响。

1 耐张线夹选型及参数

1.1 耐张线夹连接金具的选型

本文选用型号为NY-630/45的液压压缩型耐张线夹为分析对象，其中N表示耐压线夹，Y表示压缩型，630/45表示铝截面为630 mm和钢截面为45 mm。该型号本体由铝制件，其余为热镀锌钢制件，广泛应用220 kV线路中，选用NY-630/45作为研究对象，具有一定的代表性。

NY-630/45耐张线夹用以固定导线在非直线塔的绝缘子串上，常见适用的钢芯铝绞线导线型号为LGJ-630/45，该导线外径为33.6 mm，单位质量为2 060 kg/km。按照耐张线夹与钢芯铝绞线的压接规范，其结构[19-21]如图1所示。

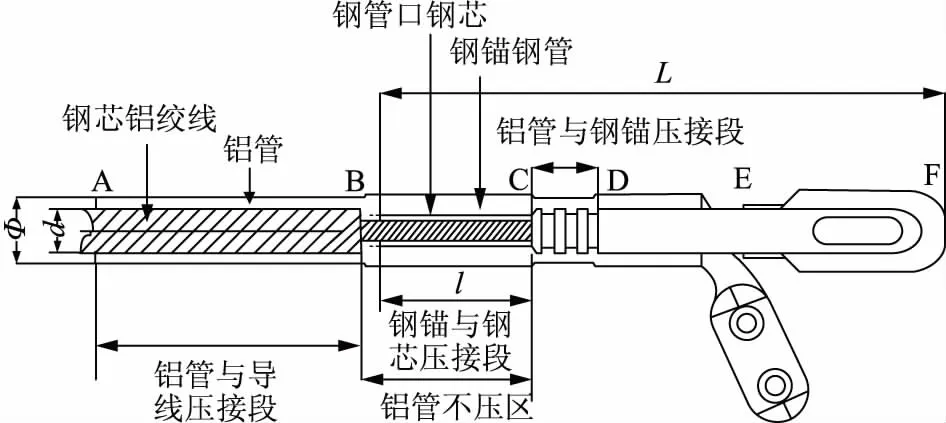
l—钢锚与钢芯压接段长度；Φ—铝管后直径；d—架空导线钢芯直径；L—耐张线夹钢锚长度。

图1 耐张线夹压接结构
Fig.1 Structure of clamping and
pressing of tension wire

在线夹安装过程中，架空输电线路导线会先去除铝线部分，留下图1中BC段导线钢芯部分，钢芯与钢锚中空部分使用液压机进行压接，压接压力一般在85～90 MPa之间；图1中AB段是铝管与钢芯铝绞线的压接区域；CD段以及DE段是铝管与钢锚相互压接区域，压接所用压力和压接钢锚与钢芯大小一致，其中CD段有3个相同深度的凹槽，压接之后主要起到防耐张线夹滑动的作用，亦是本文后面重点关注研究的区域。

1.2 耐张线夹钢锚物性参数

NY-630/45耐张线夹钢锚所使用钢材原材料为Q235B(直径为36 mm)圆钢，对某批钢锚原料送检，依据执行标准GB/T 700—2006分析得到原材料的化学成分和力学性能，见表1。

经检验，样品试验的化学成分和力学性能结果满足国家标准要求。

表1中屈服强度值是一个关键指标，根据弹性力学知识可知:材料的应力-应变关系超过屈服强度便会出现宏观可见变形，材料发生塑形变形;同时超过屈服强度点之后应力-应变关系呈现非线性关系，到达抗拉强度点材料就会被拉断。本文将利用有限元计算的方法对不同凹槽深度对钢锚整体应力分布的影响进行分析。

表1 Q235B圆钢化学成分及力学性能Tab.1 Chemical components and machenical performance of Q235-type steel

2 NY-630/45耐张线夹应力分布仿真模型建立

2.1 力学模型建立

线夹钢锚在受导线张力情况下会发生微小形变，钢锚上一初始位置(x,y,z)在力的作用下位置改变为(X,Y,Z)，向量u=(u1,u2,u3)=(X-x,Y-y,Z-z)称作位移向量。由胡克定律可得

σij=λδij·u+2μεij.

(1)

式中：σij为应力张量；δij为克罗内克函数，当i=j时，δij=1，其他情况下δij=0；εij为应变张量；i、j为平面坐标方向；λ和μ为描述固体性质的常量，称为拉梅参数，其与杨氏模量E及泊松比υ的关系为

(2)

根据式(1)和式(2)可以计算出钢锚内部各个单元体的3个主应力σ1、σ2、σ3，3个主应力与其各个受力平面的法向平行，根据这3个主应力可以计算出Von Mises屈服准则下的Von Mises等效应力，即

(3)

Von Mises应力是根据第四强度理论(即畸变能密度理论)计算的一种等效应力[22]。实验表明，碳素钢和合金钢等韧性材料的塑性屈服实验原理和结果与这一强度理论吻合良好，钢锚为钢结构的塑形材料，因此我们选取Von Mises等效应力对钢锚应力分布进行分析。

由于钢锚凹槽部分是铝管与钢锚压接区域，同时受到导线张力和铝管挤压压力的作用，因此凹槽区域的剪切应力也是反映铝管与钢锚咬合紧密的力学指标。图2展示了钢锚在正常工作过程中的受力状态。

图2中在受力面A上剪切应力[22]为

(4)

式中：ΔFi为i方向的剪切力；ΔAj为j方向的受力面积。式(4)表明钢锚内部各处的剪应力可以取垂直施力方向所在截面的极限剪切力得到，剪切应力τij还可由第一主应力σ1和第三主应力σ3表示，即

(5)

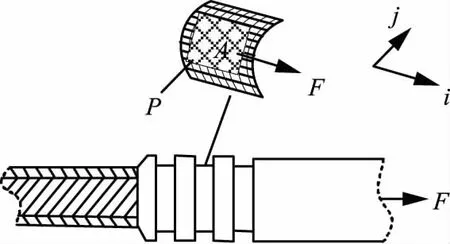
P—铝管与钢锚压接压力；F—钢锚所受导线张力。

图2 钢锚凹槽受力状态
Fig.2 Stress state of steel anchor groove

2.2 有限元建模求解流程

根据弹性力学的变分理论可以将式(1)中的偏微分方程组转换为可以用计算机迭代计算的线性方程组，这是通过将求解域网格离散化实现的，对得到的方程组引入相关约束条件，利用计算机迭代计算即可求解出位移量u，根据式(1)—(3)可以进一步计算出所求系统的应变、应力结果。

本文使用有限元仿真软件Calculix进行耐张线夹钢锚的力学仿真分析。耐张线夹钢锚的建模使用FreeCAD构建，有限元网格划分采用GMSH自适应网格划分策略，求解器采用Caculix，结果后处理采用VTK。具体的有限元建模求解流程如图3所示。

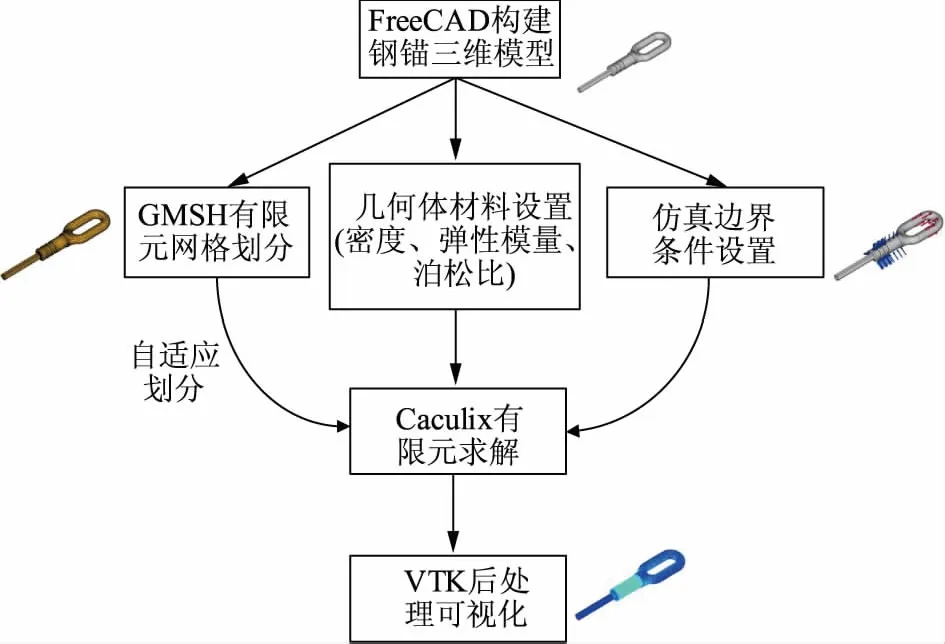
图3 有限元建模求解流程Fig.3 Process of modeling and caculating using FEM

2.3 几何建模、边界条件及材料参数设置

NY-630/45型耐张线夹钢锚的三维几何模型根据工程图在FreeCAD三维建模软件中绘制，因为分析对象是压接之后的钢锚，经压接后呈六边形，其压接后存在3个对边距S，且

S=0.866×0.933D+0.2.

(6)

式中D为钢管或者铝管外径。对钢管而言其对边距最大允许值为17.39 mm，3个对边距只允许一个达到最大值，超过规定时应查明原因，割断重接；因此在建模过程中对图1中 BC段进行了处理，将其构建为液压压接之后的模型。图4展示了钢锚实物压接图。

图4 钢锚实物图Fig.4 Actual picture of steel anchor

为求解目标力学系统组成的偏微分方程，需要给定狄里克莱边界条件(第一边界条件)、纽曼边界条件(第二边界条件)以及方程组的涉及的材料参数[17-19]。与求解常微分方程一样，如果边界条件不足会导致网格离散化后构成的高阶代数方程组奇异，即代数方程组系数矩阵非满秩，根据数值迭代理论可知代数方程奇异会导致计算结果发散不收敛，无法求解目标力学系统。对一个机械结构系统而言，其边界条件类型有固定约束、边界载荷、固定位移等，固定约束和载荷是2种最为常用的边界条件。

根据现场运行条件可以确定耐张线夹钢锚所受导线张力为20 kN，并作用在钢锚挂环部分，对应的施加边界条件为图5中的箭头位置；图1 对应BC段为钢锚与导线钢芯压接区域，铝管在此位置不再进行压接，因此设定内壁为固定约束，对应施加的边界条件位置在压接区域内壁；图1对应CE段为铝管压接区域，在现场安装中一般选取85～90 MPa液压值并且使用对应的钢模进行压接，因此在钢锚与铝管接触咬合面设置压力为90 MPa的边界载荷，对应如图5所示的箭头部分。

钢锚原材料为Q235B圆钢，根据GB 50017—2017《钢结构设计标准》进行化验检测，得到该钢材在力学仿真中涉及的材料参数见表2。

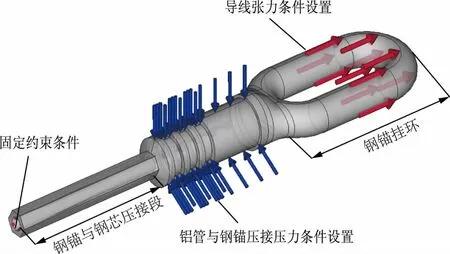
图5 仿真条件设置Fig.5 Setup of FEM simulation

表2 仿真材料属性Tab.2 Properties of material used in FEM simulation

3 耐张线夹仿真分析

3.1 耐张线夹钢锚标准模型下的应力分布情况分析

上述构建的张线夹钢锚三维有限元模型经过GMSH网格自适应划分之后送入Caculix解法器求解，得到钢锚在凹槽深度均为3 mm的标准情况下的剪切应力和Von Mises应力分布情况，如图6所示。

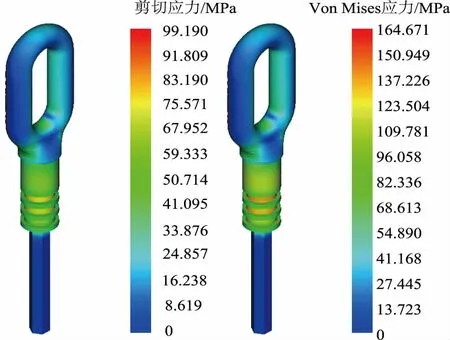
图6 钢锚剪切应力和Von Mises应力分布结果Fig.6 Distribution of max sheer stress and von Mises stress in steel anchor

从图6(a)可以看出：钢锚凹槽部分受铝管挤压咬合作用，凹槽接触面承受与之垂直的剪切应力，最大值为99.19 MPa；而在钢锚与钢芯压接部分因为不再与铝管压接，该部分剪切应力几乎为零。图6(b)是钢锚整体的Von Mises应力分布，可以看出Von Mises应力值最大的区域集中在钢锚凹槽部分，在20 kN导线张力的工况条件下Von Mises应力最大值为164.671 MPa，低于表1中的屈服强度值266 MPa，故有足够的裕度来满足实际使用条件。为分析Von Mises应力的详细分布，利用调整阈值的方法对凹槽进一步进行可视化分析，得到如图7所示结果。

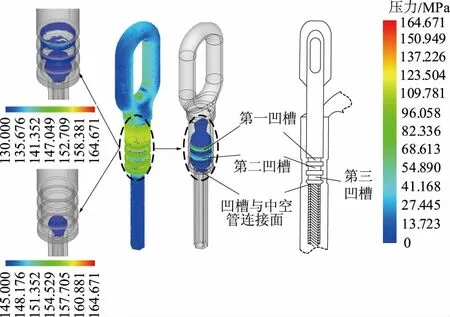
图7 凹槽区域Von Mises应力分布Fig.7 Distribution of von Mises in the area of groove

图7仿真结果表明：Von Mises应力主要集中在第一凹槽面到钢锚与钢芯连接处，在凹槽内部呈现倒锥形分布，而且应力最大最集中部分亦出现在凹槽与中空管(即压接钢芯部分)的连接面处。此结果间接验证了耐张线夹断裂事故中大都是钢锚中空管与钢锚主体部分断裂的原因是该连接面承受最严苛的应力条件，从而加速了金属疲劳效应。如果导线运行过程中由于风力等外力条件使该位置所受应力超过极限应力便会发生塑性形变，甚至直接发生断裂。

3.2 不同凹槽深度对Von Mises应力分布的影响

针对钢锚制造工艺导致凹槽深度尺寸不一的问题，在前面仿真基础上，通过调节3个凹槽深度构建了除标准模型外的另外3×9组模型(3个凹槽区域，每个凹槽构建了9组不同深度的模型)，凹槽深度尺寸为1.6～3.4 mm之间。为了便于分析，采用单一变量控制法，即每次改变一个凹槽深度，通过仿真计算得到相应的最大应力值，其结果如图8所示。

由图8结果可以看出：对于同一凹槽面，凹槽深度小于标准的3 mm深度时，钢锚最大Von Mises应力值呈现先增大后减小的趋势；深度大于3 mm时最大Von Mises应力略微增加；而标准尺寸下最大Von Mises应力值最低，第一、二、三凹槽的最大应力值分别超出其标准情况下应力值的10.5%、3.3%和3.5%，造成这种变化的原因是凹槽深度改变了钢锚的结构对称性，进而改变了主应力的分布状态。从式(3)可知：3个主应力值改变会影响Von Mises应力，当σ1、σ2、σ3任意两者之差增大计算得到的Von Mises等效应力亦随之增大，当凹槽深度低于2.0 mm时，Von Mises应力减小，此时是因为有更多钢材物质(即更多体积单元体)承受导线张力和铝管压接压力，这种作用强于对称性结构改变引起的应力增大效应。

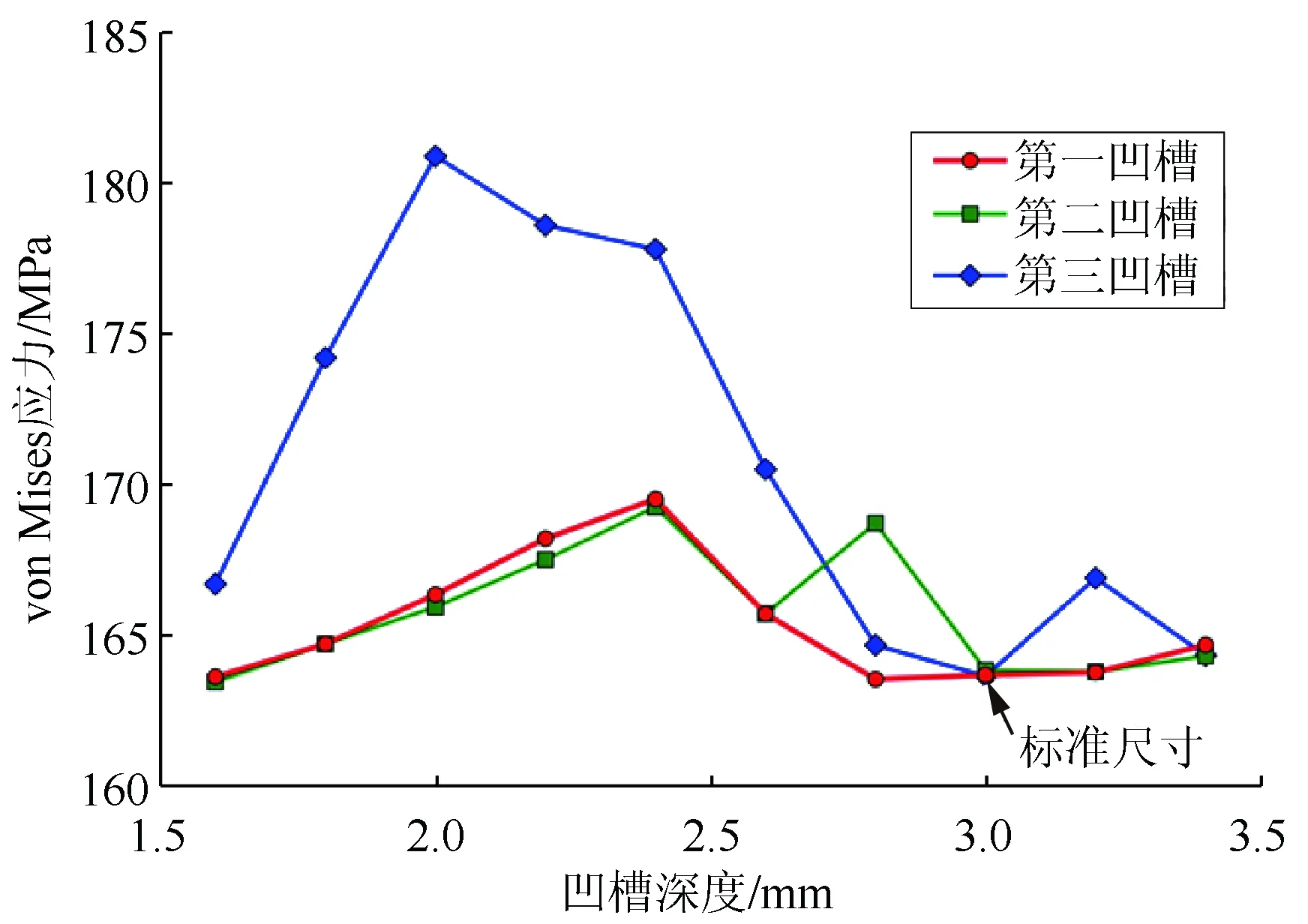
图8 不同凹槽深度最大Von Mises应力Fig.8 Maximun Von Mises stress in different depth of groove

对不同凹槽进行分析。从图8可以看出：第三凹槽的深度变化对应力值变化的影响比另外2个凹槽大，当第三凹槽深度为2.0 mm时最大Von Mises应力为180.89 MPa，比正常3.0 mm深度情况下高出10.5%，原因是第三凹槽位置靠近钢锚与导线钢芯压接部位，该区域的钢材料较少，平均单元体所受3个主应力值比其他区域大；因此在同样张力的条件下第三凹槽部分的Von Mises应力值改变相较于第二也更加明显，从而增加耐张线夹钢锚断裂的风险。图8中亦可看出：第三凹槽的深度改变对钢锚整体应力分布影响比第一和第二凹槽要大，当第一凹槽深度偏差达0.6 mm时，Von Mises应力值超出标准情况下8.6%，因此在施工作业检查某批次钢锚的时候应该着重检查第一凹槽深度是否满足标准要求。

3.3 凹槽深度对剪切应力分布的影响

凹槽深度的改变不仅会改变Von Mises应力分布，还会改变耐张线夹钢锚的剪切应力分布。根据第3.2节内容已经分析得知第三凹槽对钢锚整体力学性能的影响最大，为了探究凹槽深度对剪切应力的影响，仿真计算第三凹槽在不同深度下的最大剪切应力，结果见表3。

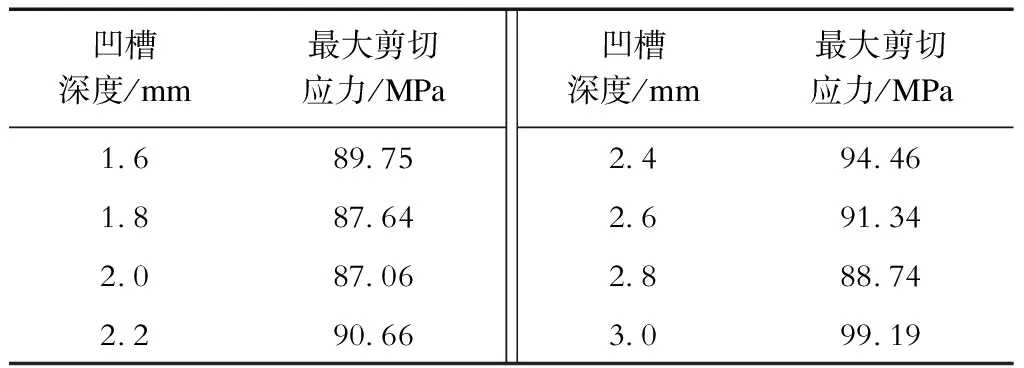
表3 第三凹槽深度与最大剪切应力关系Tab.3 Relationship between depth of third groove and max sheer stress

从表3可以看出，随着凹槽深度的减小，最大剪切应力呈现出先减小、后增大、再减小的趋势。这一变化情况需要结合前面图8结果进行分析：当凹槽深度减小为2.8 mm时，钢锚凹槽结构发生改变，单元体计算得到的主应力值亦相应发生改变，根据式(5)可知剪切应力值随第一主应力和第三主应力变化而变化，钢锚构件在结构上的改变引起的主应力变化是非线性的，亦可根据图8中第三凹槽Von Mises应力随深度变化结果得知；当凹槽深度为2.0 mm时，对应的Von Mises应力值达到最大，而此时最大剪切应力最小，其值为87.06 MPa，比正常3.0 mm深度条件下剪应力减少了12.2%，原因是第一主应力与第三主应力差值减小，而第一主应力与第二主应力差值、第二主应力与第三主应力差值增大，该结果同时说明铝管与钢锚凹槽部分的咬合摩擦作用减小，这将削弱凹槽的防滑作用，增加线夹脱落风险；当凹槽深度偏差达0.6 mm时，剪切应力较标准情况下减少4.7%。因此，凹槽深度变化会影响耐张线夹的耐张性能，降低耐张线夹的使用寿命，增加了电网运行的风险。

4 结论

本文对耐张线夹钢锚因制造工艺导致的凹槽深度不同对线夹性能的影响进行了研究，利用有限元分析的方法，构建了包括标准模型在内的28种不同凹槽深度的钢锚模型，分析了仿真得到的应力分布结果，并得出以下结论：

a)3个凹槽深度不均匀改变了钢锚结构的对称性，进而影响钢锚内部单元体的应力分布，其中第三凹槽对应力分布影响最大，当偏差达0.6 mm时，最大Von Mises应力值超出标准情况下8.6%，应力分布最集中部分在钢锚第三凹槽与钢芯压接段的连接面处，线夹断裂发生部位亦多发生于此。

b)由于制造工艺缺陷造成钢锚凹槽深度不一，最大剪切应力低于标准值，这将会增加线夹钢锚断裂以及钢锚脱落的风险。从研究结果可知，当钢锚凹槽深度偏差达0.6 mm时，耐张线夹剪切应力减少4.7%，线夹耐张性能下降；因此，在施工作业前需要对钢锚进行测量筛选，避免使用不满足标准的钢锚，从而提高电力金具在使用过程中的安全稳定性。