可变多胞体结构的鲁棒模型预测控制

杨世忠，邢丽娟

青岛理工大学 信息与控制工程学院,山东 青岛266520

1 引言

鲁棒模型预测控制（Robust Model Predictive Control，RMPC）由于能显式地表示系统的模型不确定性和输入输出约束，实现系统的稳定控制，被广泛应用于各种系统控制中[1-4]。在RMPC中，如何更好地减小由于系统的参数的不确定对系统控制造成的影响，减小系统的在线计算量，实现系统的快速稳定控制，是科研人员一直关注的重点。

鲁棒模型预测控制将系统模型的不确定性用多胞体描述，离线时优化出一系列嵌套椭圆集序列，在线时根据状态变量在椭圆集序列中的位置得到系统的控制律，这种基于离线嵌套椭圆集RMPC已经取得了许多研究成果[5-6]。文献[7]针对系统状态的多组一维子空间，运用常规离线鲁棒预测控制生成多组椭圆不变集序列，在线时寻求当前状态所处最大椭圆不变集，通过简单的融合计算得到对应的控制律。文献[8]离线构造一系列椭圆集来描述多步可行区域，每个椭圆集的平衡点根据上一个椭圆来选取，再根据在线计算合适的输入使系统稳定，采用逐步倒退计算的方法确保迭代的可行性和稳定性，减少了计算负担。文献[9]针对一类具有多胞不确定性的线性参数变化系统，通过求解线性矩阵不等式，构造了一个收缩的椭圆集序列，优化了离线不变椭圆集的数量，实现了系统控制的快速稳定控制。由于系统的输入输出约束一般采用不等式的形式给出，采用离线嵌套椭圆集的RMPC 的初始可行域较小，算法保守，因此，采用一系列嵌套多面体集的离线算法开始广泛应用于RMPC 中[10-12]。文献[13]离线时构建多面体不变集，在线时每一个采样时刻确定包含当前状态的最小多面体不变集，通过计算与相邻两个多面体不变集的位置关系得到状态反馈控制律。文献[13]离线时选取一系列收敛于原点的离散状态来计算相应的状态反馈控制律，并构造各多面体不变量集。在线时，通过确定当前测量状态可以嵌入的最小多面体不变量集来确定系统的控制律。文献[14]提出了一种基于鲁棒一步集的Tube不变集鲁棒模型预测控制方法，采用多面体不变集离线设计方法得到基于多面体不变集序列的扩展终端约束集，通过引入鲁棒一步集并借助Tube 不变集控制策略，设计了基于鲁棒一步集的鲁棒模型预测控制方法。文献[15]考虑了离散时间的不确定分段仿射系统，提出了一种基于检测状态空间区域的可达性的多面体RMPC 算法，保证系统状态从最大集驱动到目标区域，减少了在线计算量。文献[16]中的RMPC 算法针对线性变参数系统，离线时构造了与嵌套多面体不变集相关联的控制律序列，在线时经过线性插值的方法确定系统的实时控制律。应当看到，以上多面体不变集是在系统多胞体结构不变的基础上由输入输出约束来确定的，由此产生的多面体也具有一定的保守性，而采用未知但有界误差估计，用数据驱动的策略可以更好地估计不确定性多面体。文献[17]采用未知但有界误差估计的方法，提出了一种不确定多胞体的递推估计RMPC，在每个采样周期对多胞体结构进行更新，改善了系统的控制效果，但由于该算法采用在线优化的方式，造成系统在线运算负担较重。

在以上文献的基础上，为适应状态变量的变化对多胞体结构的影响，减少在线运算量，提高控制的精确性，采用如下设计方法：将控制算法分为离线算法和在线算法两个部分，离线算法根据系统状态变量的变化，得到相应的可变参数多胞体结构，并将其转化为便于优化运算的状态空间多胞体形式，构建一系列离线嵌套多面体不变集。在线算法根据状态变量在嵌套多面体不变集中的位置，结合可变多胞体结构，采用线性插值的优化方式得到系统的实际控制律，以实现系统的快速稳定控制。

2 问题描述

给定一个线性变参数系统：

其中，x(k )∈Rn为系统状态变量；u(k )∈Rm为系统控制输入；y(k )∈Rny为系统输出。

由于系统（1）的参数可变，所以状态方程系数矩阵A,B 具有不确定性，可用凸多胞体约束来表示：

这样，状态方程系数矩阵A,B 可表示为：

同时考虑系统（1）的输入、输出约束：

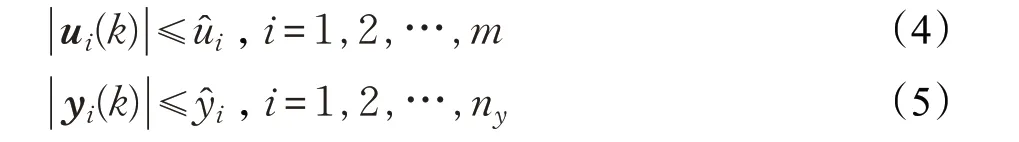
对上述线性变参数系统，采用最小最大优化方式：

选择李亚普诺夫函数：

使系统（1）满足不等式：

由公式（8）推导出J∞()k 的上界γ，则有：

设系统的状态反馈律为F，则有：

令F=YQ-1，则公式（6）的优化可采用以下线性矩阵不等式的形式：

其中，公式（11）是优化目标，公式（12）是系统状态变量的椭圆集约束，公式（13）是李亚普诺夫稳定的条件，公式（14）和（15）是输入、输出约束。

在常规的算法中，多胞体结构是固定的。设计的目的是在离线算法中考虑系统状态变量的变化而导致的多胞体结构的变化，并根据变化的多胞体结构构建嵌套多面体不变集。在线时根据状态变量在嵌套多面体不变集的位置，同时考虑多胞体结构的变化，通过线性插值的方法得到系统的实时控制律。

3 多胞体的未知但有界误差估计

由于系统的状态变量在不断的改变，系统的多胞体结构也会相应发生变化，为了能根据状态变量的变化而得到相应变化的多胞体结构，采用未知但有界误差的方式来对多胞体进行估计。由于直接由未知但有界误差的方式得到的可变参数多胞体不方便进一步优化运算，所以需要将可变参数多胞体转化为适合于线性矩阵不等式优化的状态方程系数矩阵多胞体的形式。因此，设计思路是首先通过未知但有界误差估计的形式得到线性可变参数多胞体，然后，再经过变换得到状态方程系数矩阵多胞体，以便采用线性矩阵不等式进行优化。

由于多胞体结构是由系统（1）状态方程系统矩阵中的可变参数决定，为了体现可变参数和系统可测量的变量的关系，系统（1）需要转换成未知但有界误差描述模型：

其中，z(k )∈Rs为系统可测量变量，φ(k )∈Rr为系数矩阵，θ ∈Rr×s为系统的不确定参数，e()k 为有界误差，满足：

由公式（16）、（17）可得：

将公式（16）表示为空间集合的形式：

设系统（1）的可变参数的初始多胞体为Ωθ1，依次第i 个可变参数多胞体为Ωθi。这样在计算离线的第i个可变参数多胞体结构可采用以下公式：

由公式（21）可以看到，当系统的状态发生变化时可变参数多胞体的结构会发生变化，因此在实际的控制过程中考虑多胞体结构变化对系统的影响，有利于实现系统的稳定控制，减少由于多胞体固定不变带来的保守性。由于鲁棒模型预测控制算法优化时采用的是状态方程系数矩阵，因此，需要将得到的可变参数多胞体结构化成状态方程系数矩阵多胞体的形式。

对应系统（1）的状态方程系数矩阵A,B 因包含未知参数导致其具有不确定性，根据公式（16）可知θ 是A、B 中的不确定参数变量。若，结合公式（2）可以得到系统的可变参数和状态方程系数矩阵的关系：

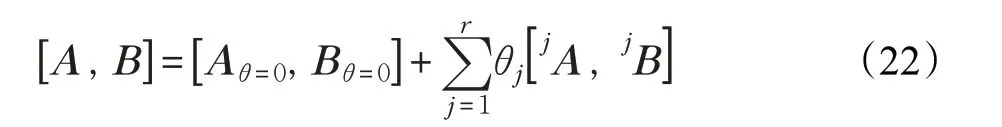
其中，Aθ=0、Bθ=0是A、B 中令θ=0 得到的矩阵，jA、jB 是A、B 减去Aθ=0、Bθ=0后以对应每个不确定参数变量的系数矩阵。

4 RMPC离线算法

为减少在线运算量，采用离线算法得到一系列基于可变多胞体结构的多面体不变集和相应的控制律。在离线算法中，首先通过给定一系列状态变量，结合多胞体结构的改变，优化得到一系列控制律；然后依据优化出的控制律，根据系统的输入输出约束得到相应的一系列多面体集。

算法1 对于系统（1）和输入输出约束（4）、（5），设定有界误差界限emin、emax，根据系统（1）参数可变范围得到可变参数初始多胞体为Ωθ1。给定L 个逐渐向平衡点靠拢的状态变量xi，令i=1。

（1）若i=1，将xi代入式（11）～（15）优化得到系统的控制律Fi；若i ＞1，转到（2）。

（2）根据已得到的控制律Fi-1和当前的给定状态变量xi得到系统的输入输出等相关变量，将系统（1）转化为未知有界误差描述模型（16）。

（3）由公式（19）、（20）得到当前的可变参数变量空间集合Hup、Hdown。

（4）由公式（21）得到第i 个可变参数多胞体Ωθi。

（5）由公式（22）计算系统状态方程系数矩阵的多胞体，代入公式（13）和（15），再优化式（11）～（15）得到控制律Fi。

（6）令i=i+1，若i ≤L，返回（1）；否则，算法结束。

算法1首次计算控制律时，采用的是系统的可变参数初始多胞体，在此基础上通过不断优化得到L 个不同结构的可变参数多胞体，经过变换得到不同结构的状态方程系数矩阵多胞体，并求解出相应的控制律。然后，通过算法2得到离线嵌套多面体不变集。

算法2 对于系统（1）和输入输出约束（4）、（5），通过设定的状态变量xi，由算法1 得到L 个状态方程系数矩阵多胞体和控制律Fi。

（1）令i=1,m=1。根据输入输出约束，设对于每个xi和控制律Fi对应的多面体不变集为Si={x|Mix ≤di}，其中：

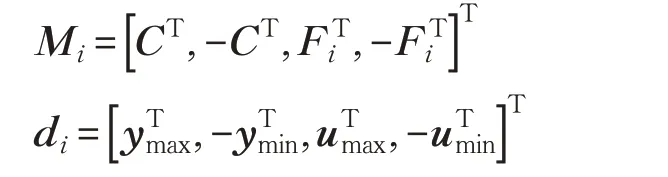
（2）取( Mi,di)的m 行，采用系统状态方程系数矩阵多胞体进行优化求解：

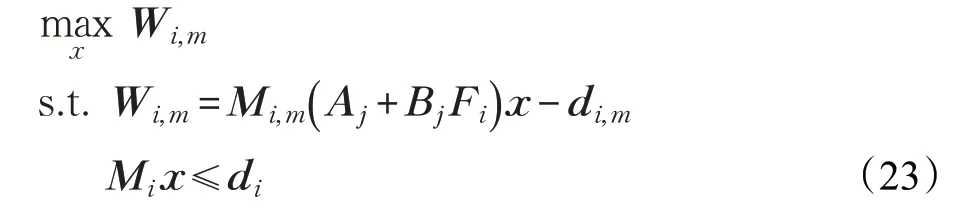
若Wi,m＞0，说明原来的不变集需要添加约束Mi,m( Aj+BjFi)x ≤di,m，则：

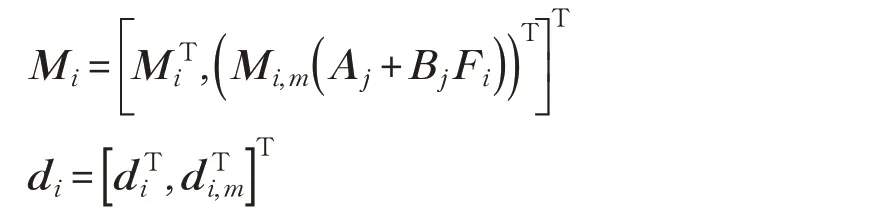
（3）令m=m+1，如果m 不大于( Mi,di)的行数，返回步骤（2）。

（4）令i=i+1，如果i ≤N，返回步骤（1）；否则算法结束。

离线算法2中，对于嵌套多面体不变集的优化求解过程中，对于给定的不同状态变量，都采用相应多胞体结构进行优化，这样更符合系统控制的实际情况。

采用离线算法中得到系统的可变多胞体结构、相应的控制律和嵌套多面体不变集，使得在线运算时只需要根据状态变量在嵌套多面体不变集中的位置，通过插值优化就可得到系统的实际控制律，减少了系统的在线运算量。

5 RMPC在线算法

在线算法根据系统状态变量的当前值x(k)在嵌套多面体不变集中的位置，寻找状态变量处在哪两个多面体不变集之间，并通过由离线算法得到的控制律进行线性插值优化得到实时控制律[18]。在计算的过程中，需要考虑多胞体结构的变化。

算法3 对于系统（1）和输入输出约束（4）、（5），由离线算法得到L 个离线多面体不变集及相应的控制律和状态方程系数矩阵多胞体结构。

（1）根据当前状态变量x(k)，寻找其所处的最小多面体不变集Si。

（2）若i ＜L，进行以下优化问题的求解：

（3）若i=L，则u(k)=FLx(k )。

（4）将u(k )代入系统（1），实现对系统的稳定控制。

在算法3中，λFi+(1 -λ )Fi+1是采用线性插值计算得到的实时控制律，Fi和Fi+1是状态变量所处的最小多面体集和下一个更小的多面体集对应的控制律。得到实时控制律后，由公式（10）确定系统的输入量，实现系统的稳定控制。

定理1 对于线性变参数系统（1），满足输入输出约束（4）、（5），若系统初始状态变量x1∈S，S 为多面体集，则算法3可以保证闭环系统的渐近稳定。

证明由于算法3是在可变多胞体结构的基础上进行的，首先说明由可变参数多胞体转换的状态方程系数矩阵多胞体的嵌套关系。设在离线算法相邻的两个θ的多胞体为Ωθi和Ωθ（i+1），由公式（21）可知Ωθ(i+1)⊂Ωθi，根据凸多胞体理论有：

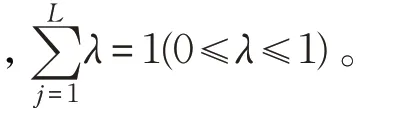
根据公式（22），设与之对应的状态方程系数矩阵多胞体为Ωi和Ωi+1。根据公式（22）和（25）可得：

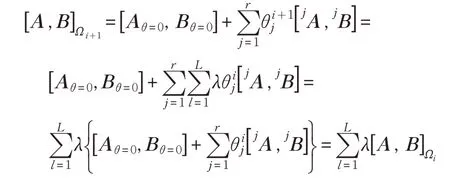
即Ωi+1⊂Ωi。这说明在状态方程系数矩阵多胞体集合也是嵌套的。

下面说明系统的稳定性，对于x1∈S，不失一般性，设k 时刻有x(k )∈Si，且，选择李亚普诺夫函数如公式（7），则，根据公式（8）可知Vi( x( k +1) )＜Vi( x(k ))；由于Si+1⊂Si，Ωi+1⊂Ωi，则Vi+1( x( k +1) )＜Vi( x( k +1) )。综上可得Vi+1( x( k +1) )＜Vi( x(k ))，即V( k+1) ＜V(k )，由此可知，算法3 可以保证闭环系统的渐近稳定。

6 仿真

以经典角度定位系统为例，系统由电动机驱动的在平面原点的旋转天线组成。控制问题是使用输入电压的电机令天线旋转，使其始终指向平面上运动物体的方向。以天线的角度位置和天线的角速度为状态变量，天线的运动可以用下列离散时间方程来描述：

输入约束条件：

参数变化范围：

系统的初始值为x(0)=[0.05;0]。

现在的RMPC为减少在线计算量，都采用离线算法和在线算法的方式，离线算法得到嵌套多面体不变集和对应的控制律，完成大部分运算量，这样在线算法的计算量就会大大减少。仿真对比也采用这种方式进行比较，对系统（26）采用可变多胞体结构的多面体不变集RMPC 和常规的多面体不变集RMPC[14]之间进行仿真比较。

根据公式（16），将系统（26）转换成未知有界误差描述模型：

由公式（28）可得系统（29）的可变参数初始多胞体Ωθ1为：

状态方程系数矩阵初始多胞体Ω1为：

常规的RMPC 中多胞体为Ω1，在整个控制过程中保持不变。

对于系统（26），由公式（22）可知，关于可变参数多胞体和状态方程系数矩阵多胞体的转化系数矩阵为：

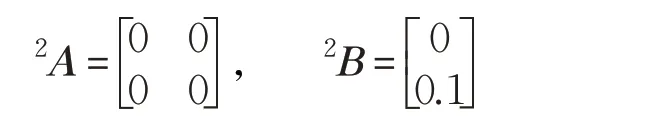
离线算法选择5个状态变量，如下所示：

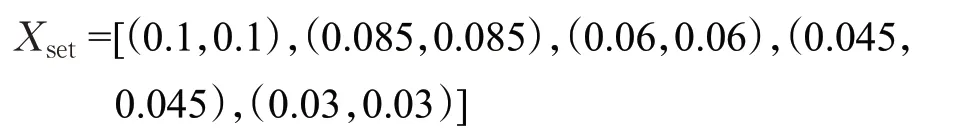
根据算法1，设置e(k)的极值为0.003，得到关于系统可变参数的5个多胞体，如图1所示。

图1 可变参数多胞体结构

由图1可以看到，当系统的状态变量逐渐趋于平衡点时，可变参数的多胞体结构也在不断减小，是一个嵌套的多胞体集。对于常规的多面体不变集RMPC，可变参数多胞体结构如图1 中的多胞体1，在控制过程中不发生变化。

由算法1可以得到相应的控制律F：

采用同样的给定状态变量值，给出常规多面体不变集RMPC离线算法得到的控制律F′：

比较两种控制律，可以看到，当状态变量趋于稳定点时，控制律作用是逐渐增大的。另外，由于在第一个控制律求解时，两种算法的状态方程系数矩阵初始多胞体是相同的，所以两种算法的第一个控制律是相等的。由于可变多胞体结构更符合实际的控制过程，所以得到的其他4个控制律都大于多胞体不变时得到的控制律。通过算法2 离线得到可变多胞体结构的嵌套多面体不变集，如图2所示。

图2 可变多胞体结构的嵌套多面体不变集

在线仿真时，将算法3 实现的控制过程和文献[14]中常规控制过程进行比较。两种算法得出的控制仿真图如图3、图4所示。

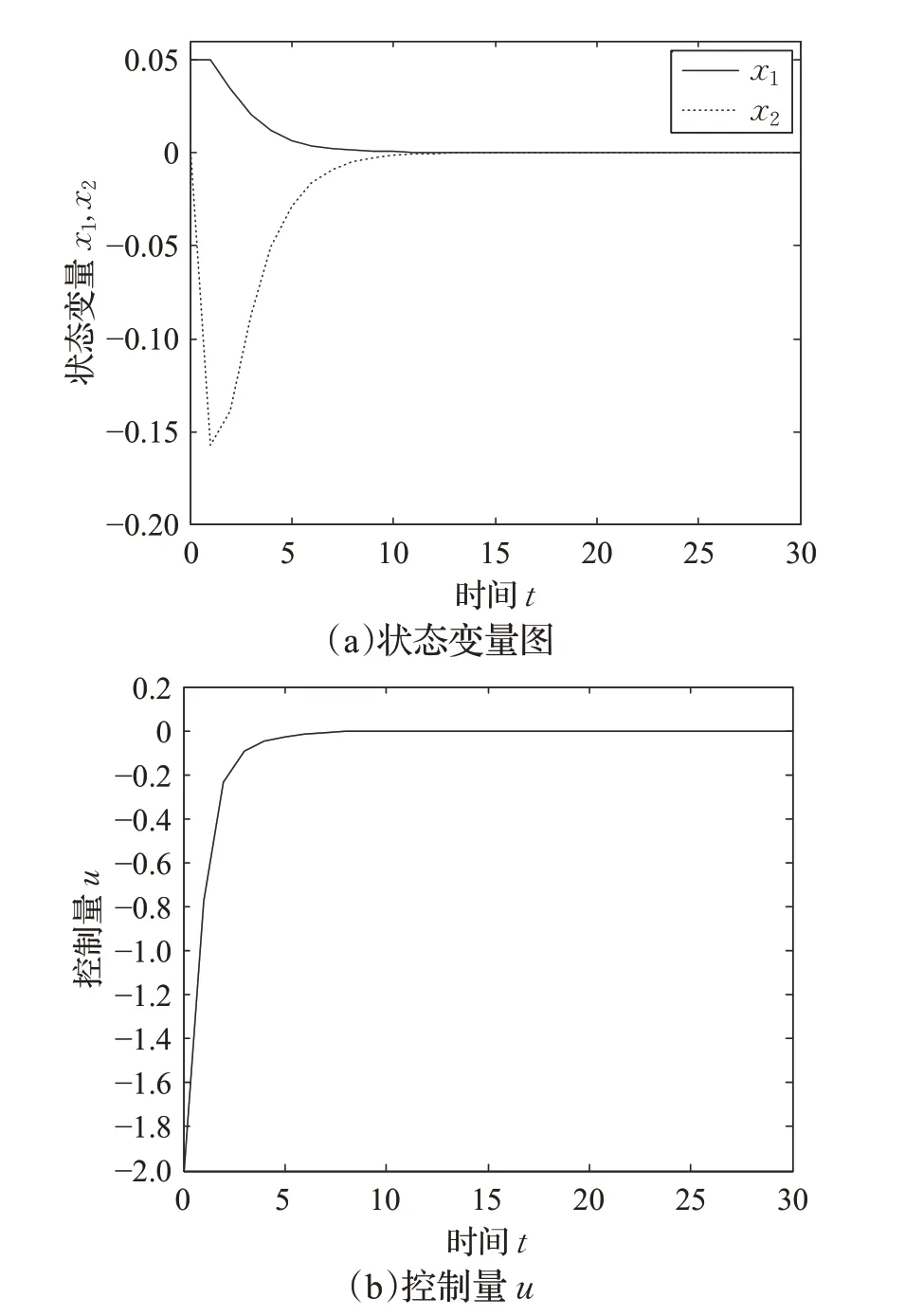
图3 可变多胞体结构的RMPC算法

比较图3、图4 可以看到，采用可变多胞体结构的RMPC算法，状态变量变化快，在第12个采样周期就可以达到稳态点；而采用常规RMPC 算法时，状态变量需要30个采样周期才趋于稳定点。采用可变多胞体结构的RMPC算法，控制量较大，对系统的作用强，在第8个采样周期控制量达到稳态点；而采用常规RMPC 算法，控制量较小，对系统的作用较弱，需要24个采样周期控制量才趋于稳定点。

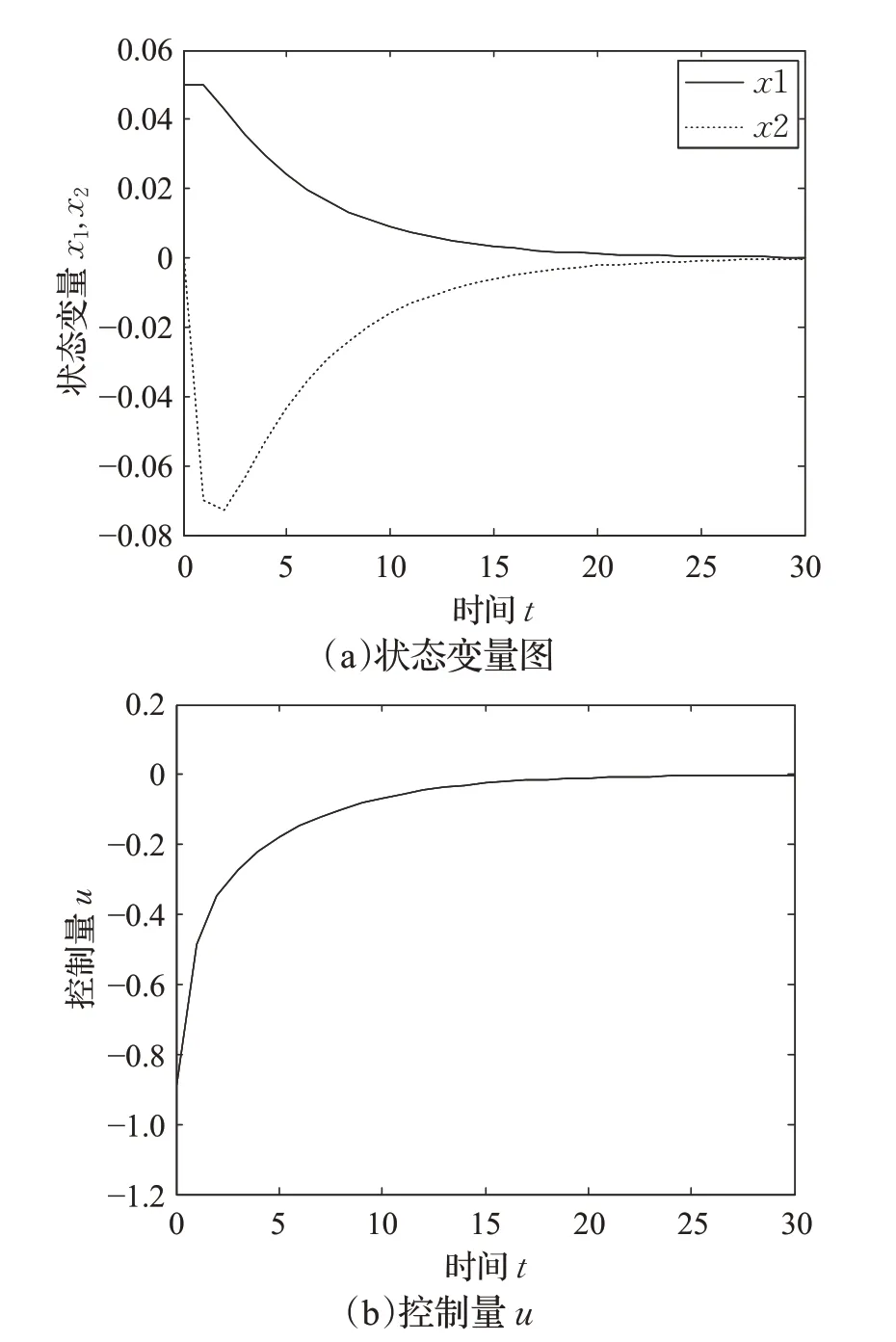
图4 常规RMPC算法

仿真结果表明，采用可变多胞体结构的RMPC算法时，由于多胞体结构可以随着状态变量的变化而进行调整，在状态变量趋于稳定点时，控制律的作用也不断增大，这样，系统控制量作用增强，加快了系统趋于稳定的速度，因此，系统响应的快，稳定性好。

7 结论

对于线性变参数系统，提出可变多胞体结构的多面体不变集鲁棒模型预测控制优化算法。采用多胞体的未知有界误差估计的方法，将线性变参数系统状态方程转换成未知有界误差描述模型。离线时，通过未知有界误差描述模型和一系列给定的状态变量，得到关于可变参数的多胞体结构，并构建嵌套多面体不变集序列。在线时，根据测量到的状态变量在系列多面体不变集的位置，考虑可变多胞体结构，通过线性插值的优化方式得到实际控制律。算法考虑了多胞体结构的变化对系统控制的影响，增强了系统的控制作用，实现了系统的快速稳定控制。通过仿真比较验证了算法的有效性，为线性变参数系统的鲁棒预测控制提供了一种可行的控制方法。