融合用户兴趣和评分差异的协同过滤推荐算法

陆 航，师智斌，刘忠宝

1.中北大学 大数据学院 大数据与网络安全研究所，太原030051

2.中北大学 软件学院，太原030051

1 引言

协同过滤算法是当前推荐系统中应用最广泛的推荐算法，在互联网各个领域都有实际的应用价值，如商品推荐[1]、音乐推荐[2]、新闻推荐[3]。其中基于用户的协同过滤算法主要依据用户对项目的历史评分行为计算用户之间相似度找到最近邻居，预测对项目的评分，然后将评分最高的前n 个项目推荐给用户。但是，随着协同过滤推荐算法在实际中的应用，也暴露出来许多问题。例如存在着用户和项目的冷启动问题，数据稀疏性问题，可扩展性问题[4]。其中用户相似度计算不准确也是影响推荐不准确的一个主要因素之一[5]。针对这个问题，许多学者展开研究。其中考虑评分差异性是提高相似度计算的一种有效方法。文献[6]通过对欧氏距离进行归一化来消除不同维度之间的衡量尺度来计算用户相似度。文献[7]定义了一种评分差异度来优化传统的相似性度量方法。上述方法虽然一定程度上提高了推荐效果，但是方法单一，只考虑到用户对项目的显式评分信息。

研究人员发现挖掘用户对项目内在的隐式信息，如兴趣偏好，能极大提高推荐的准确性。文献[8]将用户项目评分矩阵转换为用户项目属性评分矩阵，提出了基于用户对项目属性偏好的协同过滤算法。文献[9]通过标签来计算用户的偏好和项目特征的相似度实现项目的个性化推荐。文献[10]将专家预设的标签信息引入到相似度计算过程中，弥补了评分矩阵稀疏性问题。上述方法尽管能够部分反映用户的兴趣偏好，同时有效地利用标签来解决数据稀疏性问题，但是没有考虑到用户的兴趣会随时间发生变化并且忽略了标签在项目中所占权重问题。

针对以上问题，本文从用户兴趣和评分差异两方面出发，提出了一种融合用户兴趣和评分差异的协同过滤推荐算法（Collaboration Filtering recommendation algorithm based on User Interest and Rating Difference，CF-UIRD）。首先，利用TF-IDF的思想计算用户的项目标签权重，并且在指数衰减函数基础上融入时间窗口，更加精准地反映用户的兴趣变化；然后在欧氏距离基础上设计了一种考虑用户评判准则差异、用户影响差异、项目影响差异等影响因子的评分差异相似性度量算法；最后综合考虑用户兴趣和评分差异来评估用户的最终相似度，找出目标用户的邻居用户，预测项目评分，生成推荐列表。

2 相关工作

2.1 构建相关矩阵

用户项目评分矩阵R 如表1 所示。其中n 表示项目总数，m 表示用户总数，Rmn表示用户m 对项目n 的评分。在表1上做预处理，若用户m 对项目n 有评分则将评分置为1；若没有评分则将评分置为0，构成m×n的用户项目选择矩阵R′。

项目标签矩阵F 如表2 所示。其中s 表示标签总数，n 表示项目总数，Fns表示项目n 是否包含标签s，若项目n 包含标签s，则Fns的值为1，否则Fns的值为0。

用户标签偏好矩阵P 如表3所示。其中m 表示用户总数，s 表示标签总数，Pms表示用户m 对标签s 的偏好程度。

2.2 用户评分差异

文献[11]中阐释了传统相似性度量方法存在的一些缺陷，并引入了用户间评分差异度这一概念：对于任意两个用户，对同一项目的评分差异越小则两个用户的喜好越相近，即两个用户之间的相似度越高；反之如果两个用户之间的评分差异越大则两个用户的喜好越不相近，相似度越低。其中欧式距离常用来计算用户评分差异，值越大说明个体间的差异越大，反之越小。

3 考虑用户兴趣变化的用户兴趣相似性度量算法

3.1 基于项目标签权重的用户偏好

一般来说，用户对项目的评分能够较精准的反映用户对项目的喜爱程度，而标签标注作为一种用户行为，蕴含了用户对项目内容和属性的深入理解[12]。文献[13]通过对项目的标签进行简单的计数统计来求得用户对项目标签的偏好向量，但是这种方法在计算用户对标签兴趣偏好时会出现热门标签权重较大的问题，这样就导致了被用户选择过的稀缺标签很难给用户进行推荐造成权重偏差，降低了推荐结果的准确性并且未能充分反映用户的兴趣偏好。针对以上问题，本文引入TF-IDF的思想对用户的项目标签偏好进行计算。

TF-IDF 是一种加权技术，采用一种统计方法来评估某一个特征词在一个语料库中的重要程度[14]。将其思想应用到用户偏好计算上，若用户选择某个标签越频繁，这个标签被选择的人数又越少并且这个标签在整个标签集中的占比越小，则认为用户对这个标签的偏好程度越高。公式如下：

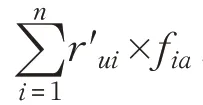
表1 用户-项目评分矩阵

表2 项目-标签矩阵

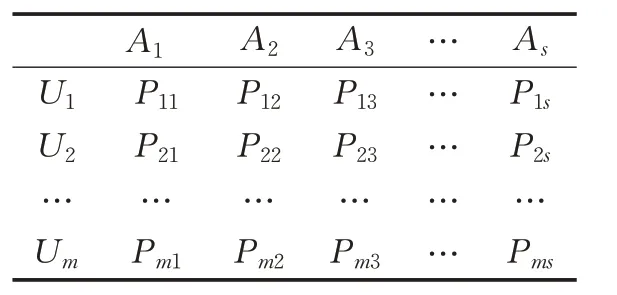
表3 用户-标签偏好矩阵

由公式（1）能够推出，若一个标签选择人数较多且在整个标签集中的自身占比较高，即热门标签，则计算结果偏低；若用户选择冷门标签，相较于其他用户而言，用户更关注此标签且该标签对于该用户的重要程度更高，这样就能在一定程度上很好的区分和明确用户的偏好，提高推荐准确率。

3.2 融入时间窗口的指数衰减函数

传统的推荐算法在处理用户对标签的偏好时常用1/0 值来标注用户是否使用此标签，这意味着随着时间的变化这些标签值是静态的，在推荐过程中所起的作用是相同的，这样就导致在推荐信息时产生低时效的问题[15]。例如用户以前喜欢功夫片，现在喜欢喜剧片，若不考虑兴趣变化，就会造成推荐误差。实际上用户的兴趣是动态变化的，用户所标注的标签也会发生变化，在标签系统中，标签具有实时性，它隐含着用户的兴趣转变信息[16]。相较于用户的早期行为，用户的近期行为更能反映用户的当前兴趣，如果要精准预测用户的当前兴趣，就要在预测过程中使用户近期标注的标签比早期标注的标签拥有更高的权重，即对时间属性赋予合适的权值，这样就能有效降低过时信息的重要性和有效缓解推荐项目老化问题，提高推荐质量，产生较好的推荐效果。文献[16]提出了一种适应用户兴趣变化的指数衰减函数，公式如下：

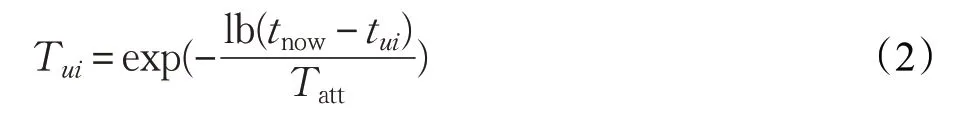
其中，tui表示用户u 对项目i 的评价时间，tnow表示用户评价项目的最大时间，Tatt表示衰减系数，代表用户兴趣衰减快慢。Tui表示用户u 对项目i 的时间加权值，即信息的衰减程度，取值范围在（0，1）之间，tui距离当前时间越近，则tnow-tui差值越小，Tui值越大，表示用户近期行为对预测有更重要的价值。

虽然指数衰减函数可以通过衰减项目影响力，即用户兴趣权重来衡量用户长期兴趣，但是用户的兴趣也不是每分每秒都会发生改变，即没有考虑用户兴趣存在短期的稳定性。例如：用户今天喜欢功夫片，不能认为第二天用户就不喜欢功夫片，这之间存在一个兴趣转变的时间缓冲期，为此引入一个时间窗口值Twin来表示用户兴趣保持稳定的时间周期，对式（2）进行改进，如下所示：

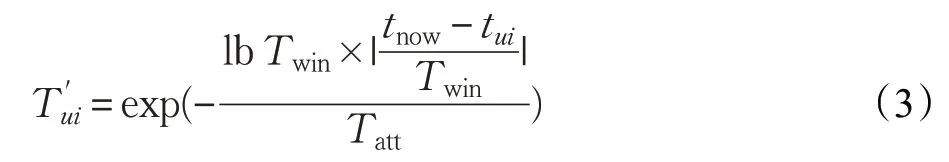
公式（3）将时间窗口引入到指数衰减函数中，弥补了指数衰减函数的不足，综合两者的优势提高了准确率，更加有效地缓解了信息过期对推荐结果的负面影响，提高推荐质量。

3.3 用户兴趣相似性计算

根据前面分析，提出了考虑用户兴趣变化的用户兴趣相似性度量算法（User Interest similarity measurement，UI）。首先将改进后的指数衰减函数添加到基于项目标签权重的用户偏好中得到用户的兴趣偏好，然后将值填充到用户标签矩阵中，公式如下：

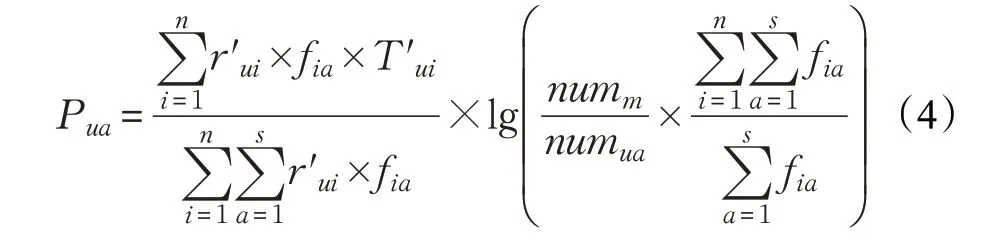
最后对欧式距离进行归一化后，根据填充后的用户标签矩阵计算UI，公式如下：

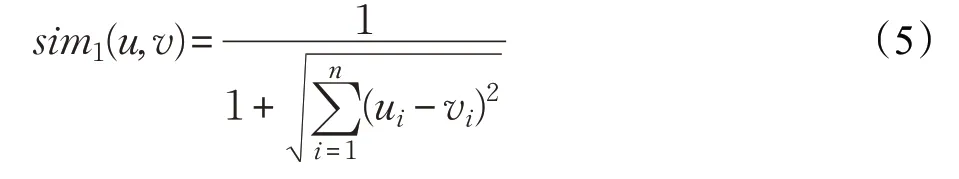
4 用户评分差异相似性度量算法

4.1 评分差异影响因素

文献[11]在求解用户评分差异时，虽然考虑了用户评判准则差异这个事实，消除了平均值差异对结果的影响，但是没有考虑到用户影响差异和项目影响差异对计算结果准确性的影响。因此本文在计算用户评分差异度时设计了一种考虑用户评判准则差异，用户影响差异和项目影响差异的度量方法。

在计算用户评分差异度时，要考虑用户评判准则差异这个事实。因为有的用户喜欢给项目打高分，有的用户则喜欢打低分。例如：在5分制的评分系统中，用户1总是给喜欢的项目打5分，而不喜欢的项目打3分；用户2总是给喜欢的项目打3分，而不喜欢的项目打1分。如果用户1 和2 同时对某个项目评分都是3 分，用传统的欧式距离进行计算评分差异度就会得到用户1和2具有相同偏好的错误结论。因此对于消除用户评判准则差异十分关键。

其次，要考虑到用户之间的影响差异。传统的相似度公式在计算用户之间的相似性时普遍认为用户之间的影响差异为0，而且传统的欧氏距离在计算用户之间相似度时仅利用共同评分项目，忽略了其他评分项目对相似度计算时的影响。例如：用户1 对4 个项目评分分别为（3，3，-，-），用户2 对4 个项目的评分分别为（3，3，2，5），如果只考虑共同评分项目，用户1和2的相似度计算结果完全相同，但实际情况是用户1只能用一半的项目评分去和用户2匹配，计算时忽略了各自评分项目对相似度计算时的影响。为了体现出不同用户之间相互影响程度的差异性，在计算用户评分差异时引入用户影响差异度，定义如下：

其中，I(u,v)表示用户u 对用户v 的影响差异。Iu∩Iv表示用户u 和v 共同评分项目集合，Iu表示用户u 评分项目的集合。用户评分项目越少，对其他用户的影响差异就越小。

在计算用户之间评分差异度时，由于项目影响的差异化，会影响计算结果的准确性。一个项目如果质量较高或较低，那么多数人对其评分都会很高或很低，利用传统欧氏距离计算用户之间的相似度结果就会偏高，而事实上这是由于项目自身质量过高或过低导致，而并非用户之间拥有共同的偏好所致，这种项目在计算用户相似度时应该让其影响度变小。针对上述情况，本文引入项目影响差异度Ii来解决项目自身质量过高或过低对用户相似性计算时导致结果偏高的影响，如下所示：

其中，Ii为项目i 的影响差异度，利用用户对项目i 的评分标准差来表示，z 为评价过项目i 的用户个数，ru为用户u 对项目i 的评分，σ 为项目i 的平均分。对于一个项目，若用户对其评分高低不同，则该项目能够很好地区分用户偏好，影响差异度权值Ii变大；相反，若用户对其评分大致相同，则该项目不能很好区分用户兴趣偏好，影响差异度权值Ii变小。为了让其计算结果保持在（0，1）区间，在计算时，对其进行最大最小归一化处理。

4.2 用户评分差异的相似性度量算法

综合考虑上述差异影响因子，在用户项目评分矩阵基础上，提出了用户评分差异相似性度量算法（Ratings Differential similarity measurement，RD）。公式如下：

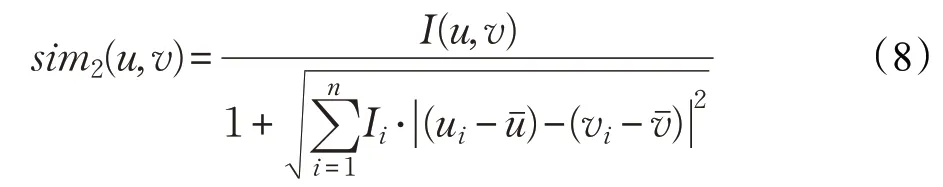
其中，uˉ和vˉ分别表示用户u 和v 评价项目的平均分，ui和vi分别表示用户u 和v 对项目i 的评分，通过两者相减来消除评判准则差异对结果带来的影响；I(u,v)为用户u 和v 之间的影响差异度；Ii为项目i 的影响差异度。sim2(u,v)值越大，用户u 和用户v 的相似度越高。

文献[17]指出，对于不同的推荐系统，应根据项目和用户的数量相对关系选择更加高效的推荐算法，基于用户相似性的推荐模型更加适用于用户数远少于项目数的情况。本文根据用户之间相似度来进行推荐，其中时间复杂度可以评估算法的效率，假设推荐系统中有m个用户，n 个项目，其中用户数远少于项目数，原始的欧氏距离衡量两个用户之间相似度的时间复杂度为O(n)，对欧氏距离改进后的用户评分差异相似性度量算法的时间复杂度为O(mn)，但是m 远小于n，因此本文提出的用户评分差异相似性度量算法在时间复杂度增加不大的情况下可以明显提升用户之间相似度的准确率，从而提高了推荐的质量。

5 融合用户兴趣和评分差异的协同过滤推荐算法

5.1 用户综合相似度

本文提出了融合用户兴趣偏好和评分差异的协同过滤推荐算法（CF-UIRD）。首先通过对sim1(u,v)和sim2(u,v)线性组合，得到融合用户兴趣和评分差异的综合相似度，公式如下：

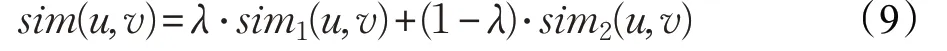
其中，权重λ ∈(0,1)，大小在实验中确定，当两个用户没有共同评分项目时λ 为1。sim(u,v)值越大，两个用户差异性越小，相似度越高。

然后在得到目标用户综合相似度之后，对项目进行评分预测，最后进行推荐，公式如下所示：

5.2 算法描述

算法融合用户兴趣偏好和评分差异的推荐算法

输入目标用户u，项目评分矩阵R，项目标签矩阵F，用户标签矩阵P，邻居个数k。

输出目标用户对待评分项目的预测评分Pui，MAE值。

步骤1 将用户项目评分矩阵R 做预处理，构建用户项目选择矩阵R′；

步骤2 根据公式（4）计算用户兴趣偏好，并对用户标签矩阵P 进行填充；

步骤3 在填充后的用户标签矩阵上，根据公式（5）计算sim1(u,v)；

步骤4 在用户项目评分矩阵R 上根据公式（8）计算sim2(u,v)；

步骤5 根据公式（9），计算综合相似度sim(u,v)；

步骤6 根据公式（10）计算用户对于候选项目的预测评分Pui；

步骤7 根据下文的公式（11）计算MAE值。

5.3 算法分析

本文提出的融合用户兴趣和评分差异协同过滤算法主要有两部分组成，一部分是考虑用户兴趣变化的用户相似性度量算法，这部分算法充分利用项目标签和时间因素，刻画了用户的真实兴趣偏好，通过用户的兴趣偏好来计算用户之间的相似度；另一部分是用户评分差异相似性度量算法，这部分算法综合考虑用户评判准则差异，用户影响力差异和项目影响力差异有效缓解了因为用户评分习惯不同，用户之间评价项目数量不同和项目质量过高过低造成的不能很好区分用户偏好和计算结果偏差问题，从而进一步提高了用户之间偏好准确度；最后通过融合这两部分算法能够更加准确刻画用户偏好，对于用户之间共同评价项目稀少，仅依靠用户项目评分计算用户之间相似性导致计算结果偏差，推荐准确率低的问题，这时可以通过用户对项目标签的兴趣偏好来计算用户之间的相似度，对单方面依靠用户项目评分计算用户之间相似度造成的误差进行修正，找到最近邻居，对用户未评分项目进行评分预测，进行推荐，从而有效缓解因为数据稀疏性导致的推荐准确率下降的问题。

对算法进行时间复杂度分析，假设有m 个用户，n个项目，s 个标签。步骤2 中计算用户对标签偏好的时间复杂度为O(mns)，步骤3中计算用户之间兴趣偏好相似度的时间复杂度为O(n)，步骤4中计算用户之间评分差异相似性时间复杂度为O(mn)，步骤5中线性加权的时间复杂度为O(1)。因此，本文算法计算用户之间综合相似度的时间复杂度为O(mns)。4.2节中提到，基于用户相似性的协同过滤推荐算法适用于用户数远少于项目数的情况，并且项目标签数在实际情况中也远小于项目数，因此本算法在不影响推荐效率的情况下更加全面准确的衡量用户之间相似度，提升推荐质量。

6 实验结果与分析

6.1 数据集

本文采用美国Minnesota 大学GroupLens 研究小组创建的Movielens100K 数据集验证融合用户兴趣偏好和评分差异的协同过滤推荐算法。数据集中记录了943个用户对1 682部电影的100 000个评分，其中每个用户评分电影至少有20 部，最低分为1 分，最高分为5 分。电影标签为：动作、冒险、动画等18个标签，每个电影可能用多个标签表示。实验中随机将数据集的80%作为训练集，20%作为测试集，在训练集上建立模型，然后在测试集上对用户评分进行预测。

6.2 评估指标

平均绝对误差MAE（Mean Absolute Error）是检验推荐系统好坏的常用标准，利用训练集中的数据经过推荐算法得到未评分项目的预测分，然后将预测评分与测试集中的实际评分进行比较，偏差越小，准确性越高。公式如下：

其中，Pui为用户u 对于项目i 的预测评分，rui为用户u对项目i 的实际评分，Test为测试集。

6.3 实验结果

首先对算法中的相关参数进行确定。本文涉及到的参数有3 个，分别为：表示用户在一段时间内兴趣保持稳定的时间窗口参数Twin、衰减系数参数Tatt和用户综合相似度中参数λ。

实验1 通过MAE值来确定时间窗口参数Twin的值，如图1所示，在K=60，Tatt的值分别为30、60、90的条件下，MAE的值都是先下降然后再上升，Tatt=30，Twin=6时，MAE 值最小；当Tatt分别为60 和90 时，Twin=5 时，MAE 值最小。在后续的实验中，将Twin的值设置为5来进行实验，认为用户的兴趣在这5天内不会发生变化。

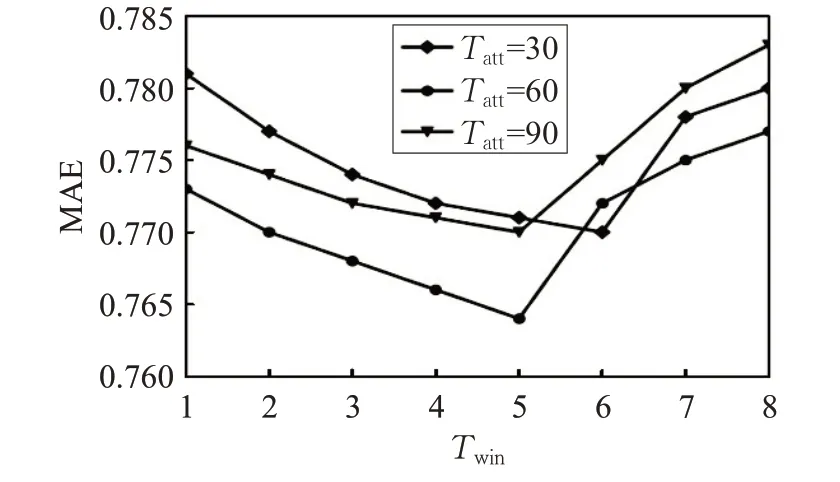
图1 不同Twin 值对应的MAE

实验2 通过MAE 的值来确定最佳时间衰减参数Tatt的值，如图2 所示，在K=60，Twin=5，Tatt的值分别为30、40、50、60、70、80、90 条件下，MAE 的值逐渐下降然后上升，在Tatt=60 时，MAE 值达到最低，因此，设置Tatt=60。

图2 不同Tatt 值对应的MAE

实验3 确定综合相似度中参数λ 的值，当λ=0 时，表示通过用户评分差异来计算用户之间的相似性，当λ=1时，表示通过用户兴趣来计算用户之间的相似性。如图3所示，在K 分别为30、60、90的条件下，MAE值逐渐下降后上升，λ=0.2 时，MAE值最小，推荐效果最好。

图3 不同λ 对应的MAE值

实验4 在不同近邻情况下，比较了不同相似度算法的准确度，其中相似度计算包括：采用传统的欧氏距离算法（ED），采用TF-IDF算法（TF-IDF），采用本文第3章提出的考虑用户兴趣变化的用户兴趣相似性度量算法（UI），本文第4章提出的考虑用户评分差异的相似性度量算法（RD），最后是融合用户兴趣和评分差异的协同过滤推荐算法（CF-UIRD），如图4所示。随着近邻个数的增加，5种算法的MAE值逐渐变小，在近邻等于80之后，MAE的值趋于平缓。本文设计的RD算法比传统的ED算法在推荐准确度上有显著的提升，本文设计的UI算法比传统的TF-IDF 算法也有小幅度提升，最后融合用户兴趣和评分差异得到的CF-UIRD 算法的MAE 值始终小于其他4种推荐算法，推荐准确度最高。

图4 5种算法对应的MAE值

7 结束语

本文针对传统的基于用户的协同过滤算法中用户相似度计算不准确的问题，将用户对项目标签的偏好、用户评判准则差异、评分值差异、用户影响差异和项目影响差异等因素融入到基于用户的协同过滤算法中，并且将指数衰减函数和时间窗口融入到改进的用户兴趣偏好中来表示用户的兴趣变化，提出了融合用户兴趣和评分差异的协同过滤推荐算法。实验结果表明，提出的算法能够更加准确的找到目标用户的邻居集用户，并且提高了推荐的精度。但是本文的推荐算法是将特征独立考虑，并没有讨论特征与特征之间的交互关系，例如女性喜欢看言情剧，男性喜欢看功夫剧，可以看出用户的性别和电影的类型之间是有强关联性的。因此，下一步工作将挖掘用户属性和电影属性之间的关系来进一步提升推荐的准确率。