基于粒子群算法的牵引逆变器多目标优化控制策略

朱琴跃，戴 维，谭喜堂，李朝阳，解大波

（同济大学电子与信息工程学院，上海201804）

相比于两电平拓扑结构，中点钳位型三电平牵引逆变器凭借其控制灵活、输出电压等级高、输出谐波含量低等优势已被广泛应用于高速动车组中，并在地铁车辆应用中得到广泛关注。然而由于其自身拓扑结构的特点，该类逆变器工作时会出现直流侧上下分压电容电压不平衡情况，导致中点电位产生波动，从而引起输出电压发生畸变、谐波含量增大，严重影响逆变器工作性能。因此，三电平牵引逆变器的中点电位平衡控制和谐波抑制一直都是国内外学者关注的问题，如何兼顾中点电位平衡控制和谐波抑制更是逆变器控制策略优化研究的难点。

一般而言，牵引逆变器中点电位平衡控制目标［1］是为了降低直流侧分压电容电压的偏移，减小中点电位波动幅值；谐波抑制［2］的主要目标则是提高输出波形质量，减小其总谐波畸变率。针对此，现有方法主要实现了对中点电位平衡控制或谐波抑制的单目标控制，兼顾两者的有效控制方法还未见文献报道。

目前，效果较好的中点电位平衡控制策略多为基于空间矢量的控制方法［3-7］。文献［3-5］提出通过调节冗余小矢量的作用时间对中点电位进行平衡控制，该方法可实现定性控制，但控制精度不够高且没有从本质上对中点电位波动的产生进行分析。文献［6-7］则利用基于虚拟空间矢量的调制方法使输出三相电流之和为零从而实现对中点电压的全范围控制，但却无法解决计算中近似处理与累计效应造成的中点电位不平衡问题。针对谐波抑制问题，基于特定次谐波消除PWM（selected harmonic elimination PWM，SHEPWM）方法得到了广泛关注与应用［8-9］。该方法通过对开关时刻角的优化选择，达到消除特定次谐波的目的，其核心在于如何求解关于开关时刻角的非线性方程组。传统的数值求解法虽计算简单、精度较高，但在求解过程中存在对初值选取过分依赖、容易出现不收敛等问题。为此，近年来包括遗传算法［10-11］、蜂群算法［12-13］、粒子群算法［14-15］在内的相关智能算法逐渐得以应用，这些算法流程简单，不需要设置复杂的参数，在非线性函数优化和多目标优化等方面具有较大的优势。

针对上述问题，本文结合现有基于空间矢量控制以及粒子群智能算法所具有的工作基础，从分析谐波与中点电位波动产生机理入手，通过等效电路分析法分别建立了三电平牵引逆变器的负载电流总谐波畸变率与中点电位波动的计算模型，提出基于粒子群算法的多目标优化控制策略，即通过粒子群算法求得SHEPWM方法的最优开关时刻角序列，实现牵引逆变器输出电流总谐波畸变率最小前提下的中点电位平衡控制，由此优化牵引逆变器控制策略。

1 牵引逆变器优化目标模型

1.1 主电路基本工作原理

在图1所示三电平逆变器拓扑结构中，每相桥臂包含4个功率开关管Tj1～Tj4（j=a，b，c）。由分析可知，逆变器每相桥臂4个功率开关管的通断情况决定了此桥臂的开关状态：以a相为例，当Sa1、Sa2导通且Sa3、Sa4关断时，桥臂开关状态为“P”；当Sa2、Sa3导通且Sa1、Sa4关断时，桥臂开关状态为“O”；当Sa3、Sa4导通且Sa1、Sa2关断时，桥臂开关状态为“N”。

若定义三电平逆变器每相桥臂的开关状态为Sj(j=a，b，c)，其取值为1、0、—1，则当直流侧电压为Udc时，该逆变器的三相桥臂输出相电压可分别为Udc/2、0、-Udc/2。

图1 三电平逆变器主电路拓扑结构Fig.1 Main circuit topology of three-level inverter

1.2 谐波畸变率计算模型

三电平逆变器控制策略直接影响其输出电压电流的谐波大小。相比于正弦载波PWM、空间矢量PWM调制方法，特定次谐波消除PWM方法可使逆变器输出电压或电流波形谐波含量最低。该方法按照某一优化目标在电压或电流波形特定的位置设置开关时刻角，通过一定控制算法对开关角进行优化计算，根据开关时刻角产生不等宽的脉冲波形，作为逆变器各个开关管的控制信号，从而减少某些特定次数的谐波、降低输出波形的总谐波畸变率。采用该方法［9］得到的PWM脉冲波形在一个基本周期内为1/4周期对称、1/2周期反对称。假设前1/4周期内能够被独立控制的有α1～αN共N个开关时刻角，各个时刻点可按照一定优化目标和优化方法计算得到，则三电平逆变器输出相电压ujn(j=a，b，c)可表示为

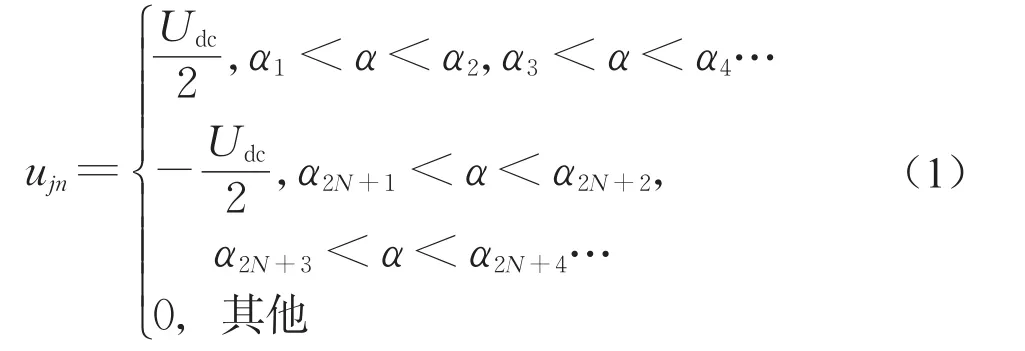
由此可知，相电压ujn(j=a，b，c)均可表示成以(α1，α2，......αN)为变量的函数，只要确定了每个基本周期前1/4周期内N个开关时刻角的值，相电压输出波形就可唯一确定，其中

进一步对相电压进行傅里叶级数展开，且考虑到在三相逆变系统中输出线电压不含3次及其倍数次的谐波，可得三电平逆变器输出线电压uL的第k次谐波有效值为

由于对逆变器供电的大多数负载特别是交流异步电机而言，真正决定和影响系统运行性能的最关键因素为负载电流［16］，故本文谐波抑制目标变量确定为负载电流总谐波畸变率。

假设用于谐波分析的异步电机等效电路如图2a所示，其中Rs为定子电阻，Xs为定子的基波漏电抗，Xm为基波互感抗，Xr为转子的基波漏电抗，Rr为转子电阻。考虑到谐波次数较高时，其第k次谐波的转差率sk基本接近于1，故进一步得到简化后等效电路如图2b所示［17］，由此可得第k次谐波的线电流有效值ILk与线电压有效值ULk之间的关系为

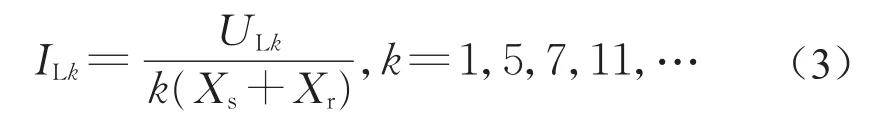
图2 异步电机等效电路Fig.2 Equivalent circuit of asynchronous motor

根据工程应用的要求，计算电压或电流谐波畸变率时最高次谐波取到50次即可［18］，为此可得负载电流总谐波畸变率为

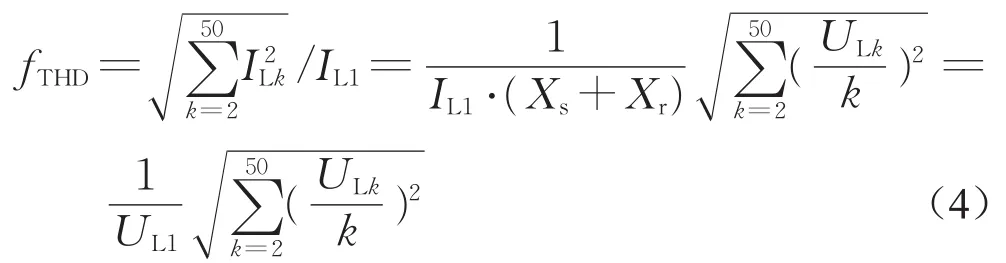
结合式（2）可得

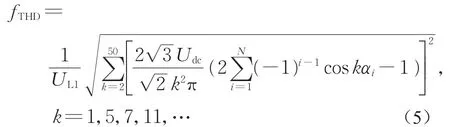
式中：Udc为三电平逆变器直流侧电压；IL1、UL1分别为负载线电流、线电压的基波有效值；αi(i=1，…，N)为1/4周期内可独立优化控制的开关时刻角。

由式（5）可以看出，电流总谐波畸变率由开关时刻角序列X=[α1，α2，...，αN]决定，对于不同的开关时刻角序列，相应计算得到的电流总谐波畸变率也不同。

1.3 中点电位波动计算模型

由上述对三电平逆变器工作原理的分析可知，逆变器每相桥臂开关状态分别取值为“1”、“0”、“-1”时，其对应的输出状态分别为“P”、“O”、“N”，相应的桥臂输出相电压则逆变器共可输出33=27种状态，每种状态对应一种电压矢量。按照其对中点电流inp的影响可将电压矢量分成如表1所示的5种类型。

表1 矢量分类Tab.1 Vector classification

如图1所示主电路中，假设C1=C2=C，由基尔霍夫电流定律可得

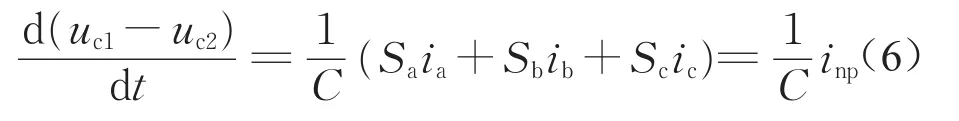
由此可得中点电位波动Δuc的瞬时表达式为

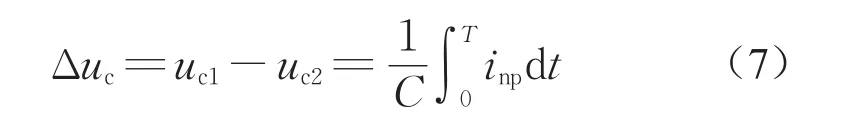
假设三相电压矢量可分别取值为1，0，—1，由此可归纳出不同电压矢量作用下中点电流inp与a、b、c三相电流ij(j=a，b，c)之间的关系为

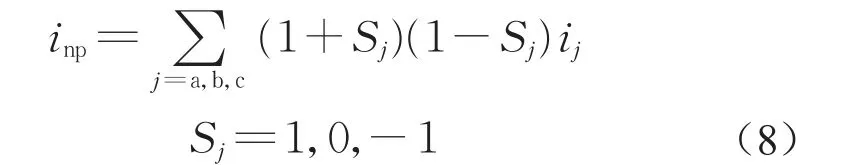
下面以上小矢量中的PPO为例，得到该矢量作用下的简化后等效电路如图3所示。其中，R为每相阻感性负载的等效电阻，相应的三相电流与中点电流分别为

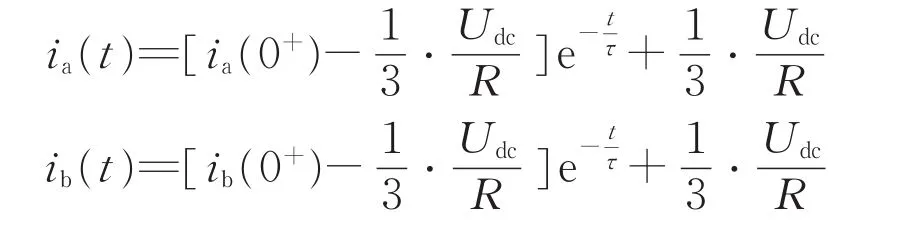
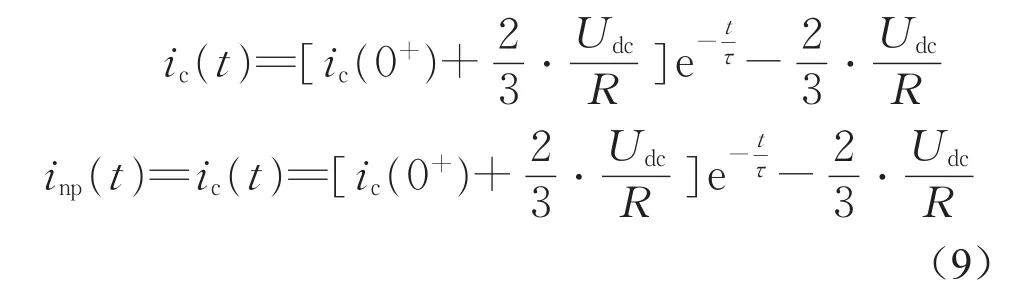
式中：τ为等效电路的动态时间常数，ia(0+)、ib(0+)、ic(0+)分别为上小矢量开始作用时a、b、c三相电流的初始值。

图3 上小矢量作用下三电平逆变器主电路等效电路Fig.3 Equivalent circuit of three-level inverter under upper small vector

同理，可得在不同矢量作用下三相电流为

由上述各式，最终可得不同矢量作用下中点电位波动Δuc为

式中：τ、R分别为不同矢量作用时对应等效电路的动态时间常数与每相负载的等效电阻；T为基本周期大小。

由式（11）可见，中点电位波动幅值的大小也与开关时刻角序列X=[α1，α2，...，αN]有关，在逆变器实际运行过程中，任意时刻t的Δuc计算过程为：

（1）根据当前时刻t的开关时刻角序列X的各个开关时刻值得到逆变器三相开关状态Sj(j=a，b，c)及对应的电压矢量。

（2）读取上一时刻逆变器的三相电流值ij(t-1)，将其赋给ij(0+)（j=a，b，c）；基于此并结合当前电压矢量，根据上式（10）计算当前时刻三相电流值ij(t)（j=a，b，c），并保存。

（3）根据上式（11）计算一个周期T内总的电压波动Δuc的幅值大小。

2 基于粒子群算法的多目标优化

2.1 粒子群算法

粒子群优化（particle swarm optimization，PSO）算法［15］是一种基于群体智能的新型演化计算技术，其中每个寻优问题的可行解都被抽象成搜索空间中的一个没有质量和体积的“粒子”。该算法首先产生初始种群，种群中每个粒子都在可行解空间运动，由自身的运动速度决定其方向和位置，每一粒子紧跟当前最优粒子运动，从而得到最优解。

在PSO算法中，如果选择n个粒子作为初始化随机种群，则在一个d维空间中，每个粒子的位置表示待优化问题的解，每个粒子性能的优劣程度取决于待优化问题目标函数确定的适应度值，粒子通过迭代不断修正自己的前进方向和速度大小，最终找到全局最优解。在种群中，假设第i个粒子的位置为Xi=[xi1，xi2，...，xid]，速度（即位置变化率）为Vi=[vi1，vi2，...，vid]；运动过程中该粒子本身所找到的个体最优解为Pbesti=[pbesti1，pbesti2，...，pbestid]，整个种群目前所找到的最优解，即全局最优解为Gbest=[gbest1，gbest2，...，gbestd]。则在迭代过程中，第p+1 次迭代计算时粒子按照式（12）所定义的方法来更新自己的速度与位置信息。

式中：i=1，2，...，n；j=1，2，...，d；p为迭代次数；r1、r2是［0，1］区间的任意随机数；c1、c2为学习因子，分别表示粒子的自身学习能力和全局学习能力；w为惯性权重，用于控制上次速度对目前状态的影响，该值根据式（13）计算而得［14］。

式中：w1、w2为权重因子；Maxgen为最大迭代次数；Ggeneration为当前迭代次数。

2.2 罚函数法

罚函数法的基本思路是对违反约束条件的非可行点或者试图穿越边界而逃离可行域的点给予惩罚，使其靠近可行域［19］。其构造思想是将约束函数进行组合组成一个“惩罚”项，加在原来的目标函数上以迫使迭代点逼近可行域，由此将约束优化问题变为无约束问题来求解处理。

对于有约束的多目标优化问题，一般可以定义为

式中 ：x=(x1，x2，...，xn)∈R为n维决策变量；f(x)=(f1(x)，f2(x)，...，fm(x))是目标函数，包含一个或者多个目标函数；g(x)、h(x)分别为不等式约束条件和等式约束条件。

由于不等式约束条件可以与等式约束条件互相转换［20］，因此，带罚函数的新目标函数可表示为

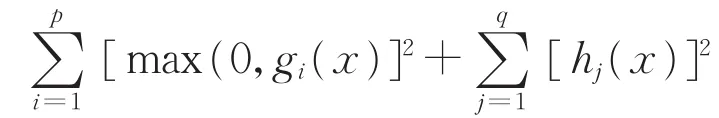
根据罚函数相关定理［21］可知，对于某个确定的M，根据上述优化方法最终求解得到的新目标函数F(x，M)的最优解即为原目标函数f(x)的最优解。

2.3 控制策略优化

2.3.1 多目标优化模型建立

拟采用基于粒子群算法的多目标优化方法来对三电平牵引逆变器控制策略进行优化研究，以实现系统输出电流总谐波畸变率最小前提下的中点电位平衡控制问题。

假设某个开关时刻角序列Xi=[α1，α2，...，αN]，相应的有约束条件的多目标优化模型可定义如下：

目标函数为

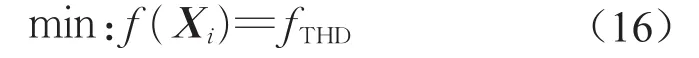
约束条件为

采用罚函数法将式（16）、（17）所描述的多目标优化问题转变为无约束的优化问题，所建新优化模型定义为

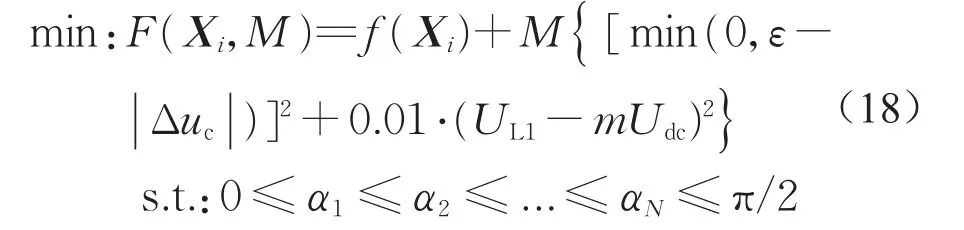
式中：M为罚因子；Udc、UL1、m、ε分别为三电平逆变器的直流侧电压、负载线电压基波有效值、调制比、中点电位波动系数上限值。

由此可得到优化模型可行解的适应度函数为

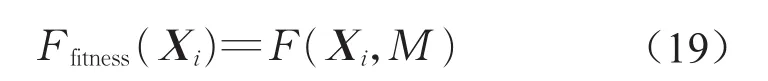
由于罚因子M为预设的定值，为方便叙述与表示，将F(Xi，M)简记为F(Xi)。

2.3.2 基于PSO算法的优化模型求解

采用PSO算法求解式（18）所建优化模型的最优解，具体算法流程如图4所示。

图4 粒子群算法流程Fig.4 Particle swarm algorithm flowchart

由图4可知，系统在初始化后，随机产生开关角序列，并计算其适应度函数值，找出个体最优和全局最优位置，更新粒子的速度和位置，并计算每个粒子更新后的适应度函数值，若此时适应度函数值优于此前的个体最优解，则将其设为新的个体最优解，若个体最优解优于此前的全局最优解，则将其设为新的全局最优解。如果迭代次数达到最大迭代次数并且惩罚项为零，则输出最优解，否则，继续进行迭代或重新进行初始化计算。

3 仿真验证

为了验证基于多目标优化的牵引逆变器优化控制策略的有效性，参考上海地铁二号线某型车的实际参数，搭建三电平逆变器仿真模型，相应参数设置为：直流侧输入电压Udc=1500V，开关频率fs=800Hz，三相输出基频f1=50Hz，调制比m=0.72；PSO算法中，初始种群个数n=40，最大迭代次数Maxgen=50，权重因子w1=0.7982，w2=0.2，学习因子c1=c2=1.4995［22］；开关时刻角初始序列为：

以电机负载为例，对其中点电位波动及输出电流谐波进行仿真与分析。假设星型连接的异步牵引电机负载的参数为：额定电压为1 050V，额定电流为132A，额定转速为1 500r·min-1，额定功率为190kW，额定频率为50Hz，功率因数为0.85，极对数为4，定子漏感0.001 511H，转子漏感为0.001 511H，定子转子互感为0.045 030H，定子电阻为0.111Ω，转子电阻为0.099Ω，电机控制方式采用开环控制。

图5所示为基于粒子群优化算法求解开关时刻角的收敛过程，由此可见，该算法在较短时间内便可寻优得到了合适的输出结果，并趋于稳定。

图6a、6b分别为采用开关时刻角优化控制前后逆变器输入侧电容电压波动波形，且选取了优化后开关角序列为

图5 粒子群优化算法的收敛性Fig.5 Convergence characteristic of particle swarm optimization algorithm

由图可知，当开关时刻角的选取未进行优化前，中点电位的稳态波动峰值为uup=9.3V，波动谷值为udown=-6.2V，总波动系数εtotal=2.07%；而对开关时刻角进行优化选取后，中点电位的稳态峰值、谷值的波动量均明显降低，总波动系数也减小为εtotal=0.96%。由此可见，本文所提的优化控制策略比传统控制策略具有更好的中点电位波动抑制效果。

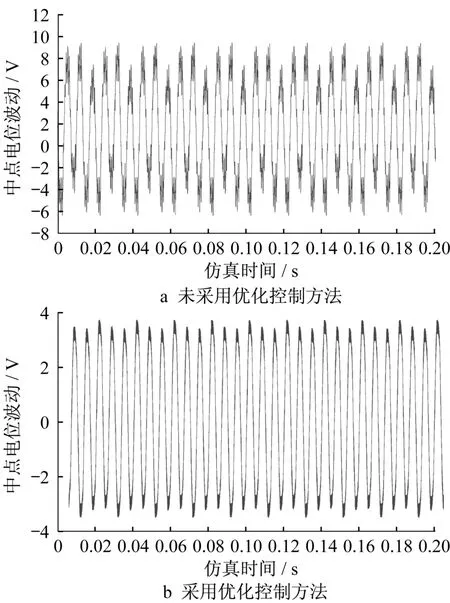
图6 采用优化控制方法前后电容电压波动Fig.6 Capacitor voltage fluctuation before and after optimization control

图7、8分别为优化后逆变器输出相电流和输出线电压频谱图，由图可知，电机负载时逆变器输出电流基频分量幅值为64.69A，THD为2.09%；输出电压基频分量幅值为1 022V，THD为23.72%；谐波主要集中在5、13、17、19次，该仿真结果与前述理论分析基本吻合，且输出电流总谐波畸变率满足实际系统运行需求。

4 实验验证

4.1 实验系统搭建

图7 输出相电流频谱Fig.7 Output phase current spectrum diagram

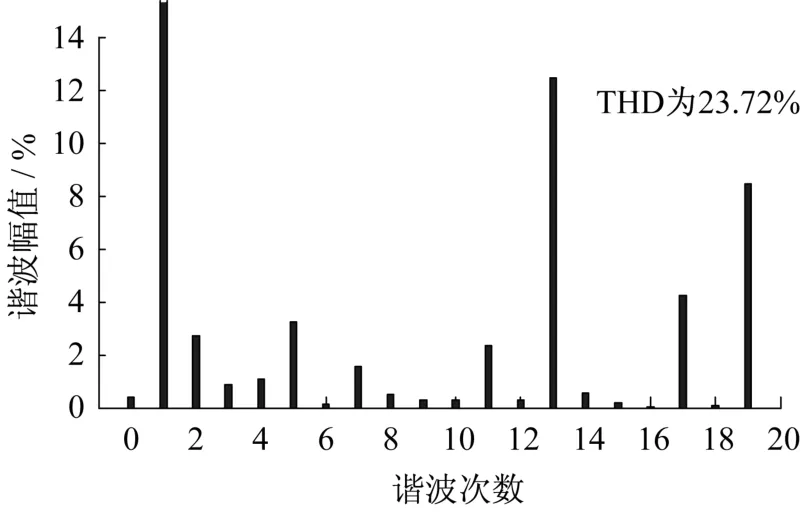
图8 输出线电压频谱Fig.8 Output line voltage spectrum diagram

搭建的实验系统如图9所示，其中，主电路主要由单相直流电源、功率开关模块、直流侧电容等组成；控制单元主要由DSP控制板、功率开关管驱动控制板等组成；负载采用三相阻感与异步电机2种类型。系统中，直流电源采用110V输入，功率开关管选用Infineon公司的FF75R12RT型两单元IGBT模块，电容选用4 700uF/160V的铝电解电容，负载采用YUP100L-4型的三相异步电机，额定功率为2.2kW，额定转速为1 500r·min-1，其余参数与仿真时相同。

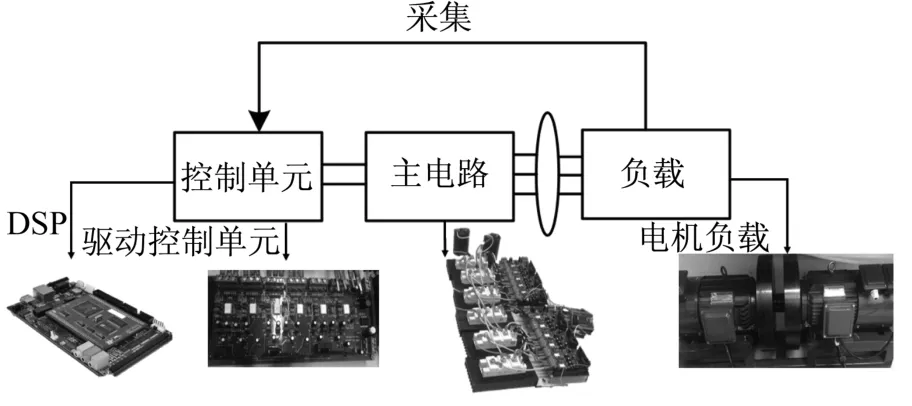
图9 实验系统图Fig.9 Experimental system diagram

4.2 实验结果分析

图10a、10b分别为采用开关时刻角优化控制前后逆变器输入侧电容电压波形。由图可知，当开关时刻角的选取未进行优化前，电容电压的稳态波动峰值为uaup=55.7V，波动谷值为ubdown=54.6V，电压波动幅值在中点电位55V左右上下波动，总波动系数εtotal=2%；而对开关时刻角进行优化选取后，中点电位的稳态峰值、谷值的波动量均明显降低，总波动系数也减小为εtotal=0.91%。该实验结果与上述理论分析与仿真结果基本一致，由此表明，本文所提的多目标优化控制方法对于逆变器中点电位波动具有较好的控制作用。

图10 采用优化控制方法前后电容电压波形界面Fig.10 Capacitor voltage waveform graph before and after optimization control

图11、12分别为优化后逆变器输出相电流、线电压波形及其频谱图。由图可知，输出相电流基频分量幅值为3.83A，THD为4.14%；输出线电压基频分量幅值为103V，THD为23.76%；谐波主要集中在5、13、17和19次。该实验结果与前述理论分析基本吻合，而输出电流、电压总谐波畸变率略高于仿真结果，这主要是由于实验与仿真中电路参数上的一些差异所导致的。

通过上述实验结果可知，本文提出的基于粒子群算法的多目标优化控制策略对兼顾谐波抑制和中点电位平衡控制具有良好的效果。

4 结论

图11 电机负载下输出相电流波形及其频谱图Fig.11 Output phase current waveform and its spectrum diagram under motor load

图12 电机负载下输出线电压波形及其频谱Fig.12 Output line voltage waveform and its spectrum diagram under motor load

针对三电平牵引逆变器中点电位不平衡以及由此而引起的输出电流谐波无法同时得到有效控制问题，采用罚函数法构建输出谐波抑制和中点电位平衡控制的多目标优化模型，基于粒子群优化算法对开关时刻角序列进行优化求解，保证输出电流谐波畸变率最小的同时极大降低了中点电位波动值，优化了牵引逆变器控制策略。仿真和实验结果表明，本文所提多目标优化控制策略对提升钳位型三电平牵引逆变器的整体性能具有较好的效果，所采用的粒子群优化算法具有较好的非线性方程求解处理能力，对工程应用具有一定的参考价值。