基于ARIMA模型分析四川省GDP

刘星辰 冯长焕

一、引言

国内生产总值（GDP）是指按市场价格计算的一个国家（或地区）所有常驻单位在一定时期内生产活动的最终成果，它不仅是核算体系中一个重要的综合性统计指标，也是我国新国民经济核算体系中的核心指标，它反映了一国（或地区）的经济实力和市场规模。无论是政府等国家机构，还是国企、跨国公司等企业，在制定目标战略时，均需参照GDP。

二、文献综述

对地方GDP进行研究是政府制定宏观调控政策的基础，许多学者通过不同的研究角度对GDP的分析方法进行了论证。

梁磊、陈晓东通过建立ARIMA模型对江苏省GDP进行分析，但其仅对GDP增长趋势进行描述而未进行预测；王鄂、张霆通过比较ARIMA模型与Holter-Winter模型的预测残差，对湖南省GDP进行分析与预测；宋平、邱燕玲运用ARIMA模型、最小二乘法以及逐步回归3种方法对青海省GDP进行分析与预测，由于研究的侧重点不同，选择因素的差异对预测残差有较大影响。

本文选取四川省1978年至2018年的GDP时间序列数据，运用B-J方法建立ARIMA模型与残差的自回归模型，通过对AIC等信息准则的比较，选取ARIMA模型对数据进行分析并预测未来短期增长趋势。

三、四川省GDP数据在ARIMA模型中的应用

（一）模型简介

ARIMA模型又称求和自回归移动平均模型，是时间序列分析中一种极为重要的方法。它是指将非平稳时间序列经过差分运算转化为平稳时间序列后，在拟合ARMA模型。

设Xt是经过d阶差分后的平稳序列，则：

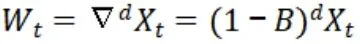
其中B为滞后算子。由于Wt是平稳序列，进而对该序列建立ARMA（p，q）模型。

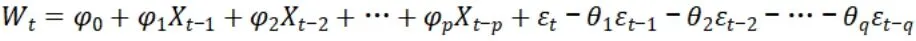
在原始数据需要通过差分将其转化为平稳序列的情况，则可利用ARIMA（p，d，q）模型进行数据分析。当进行经济数据的研究时，其大多数为非平稳的时间序列数据，故本文采用ARIMA模型对四川省GDP数据进行时间序列分析。

（二）模型识别

1.平稳性检验

从《四川省统计年鉴》中可以得到1978年至2018年四川省国内生产总值。运用EVIEWS软件将其生成时序图。从1978-2018年四川省国内生产总值的时间序列图（如图1所示）中可以大致判断该列数据呈现出无周期性的增长趋势，为非平稳序列。

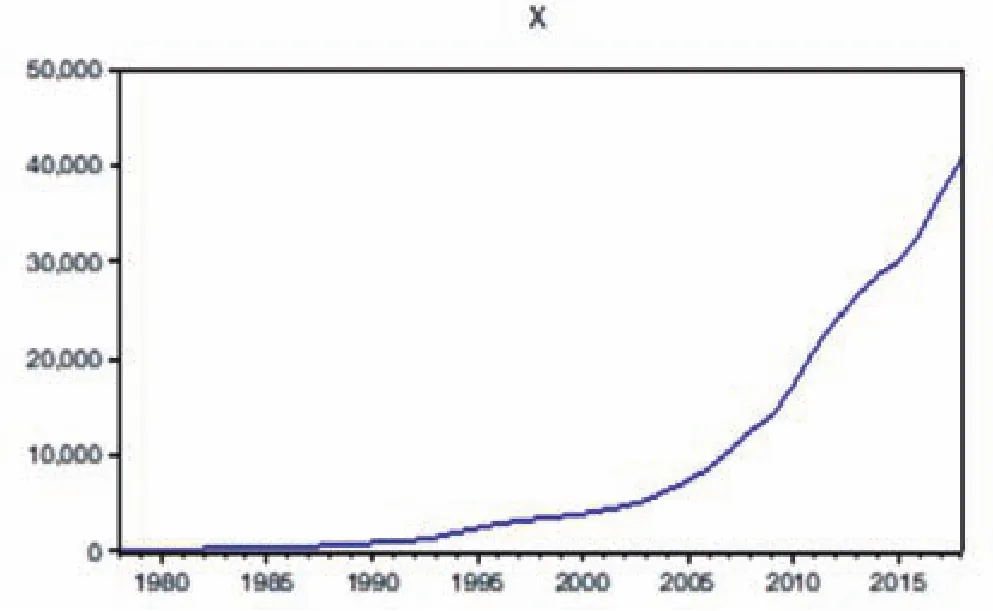
图1 四川省GDP时序图

2.纯随机性检验

从该列数据的自相关-偏自相关图（如图2所示）中可得出，Q统计量所对应得P值均小于0.05，应拒绝原假设，说明该序列为非纯随机序列，即是该序列蕴含相关信息，序列的历史信息对未来有影响，具有研究价值。

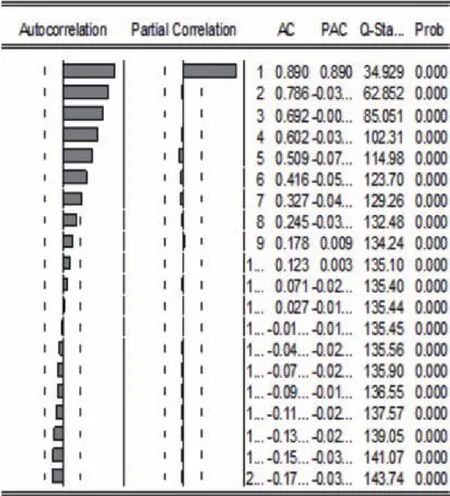
图2 GDP序列的自相关-偏自相关图

3.平稳化处理

去增长趋势：通过对时间序列图（图1）的初步定性分析可知，该序列含有非周期性增长趋势，故对该序列进行一阶差分，而一阶差分后的GDP序列仍存在增长趋势，为非平稳序列，故再对该序列进行一次差分。从图3可以看出，二阶差分后的GDP序列在0附近上下波动，为零均值的平稳序列。再对该序列进行纯随机性检验，结果如图4所示，部分Q统计量所对应的P值小于0.05，应拒绝原假设，说明该序列为非纯随机序列，即是该序列蕴含相关信息，序列的历史信息对未来有影响，具有研究价值。

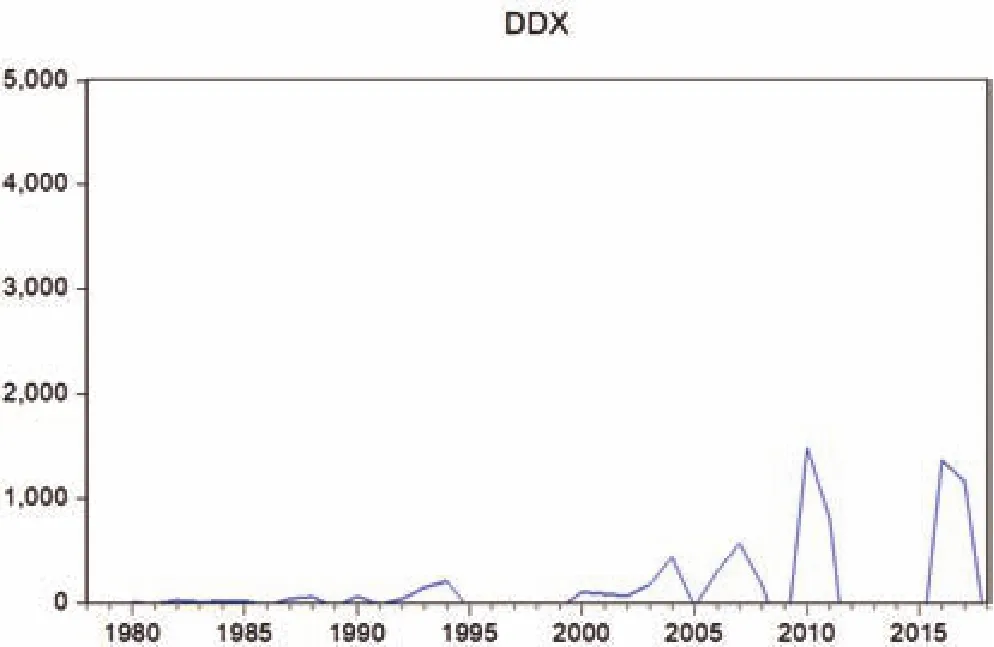
图3 二阶差分后GDP序列的时序图

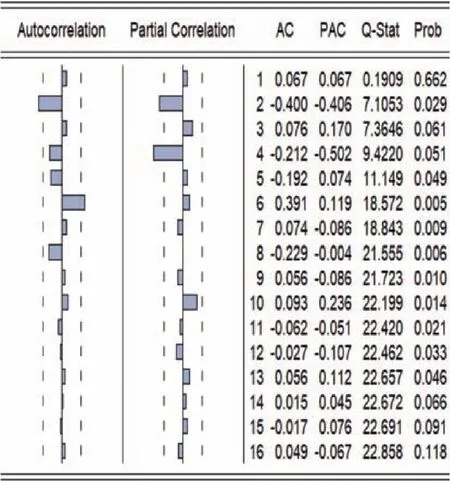
图4 二阶差分后GDP的自相关-偏自相关图

（三）建立ARMA模型

从二阶差分后的GDP序列的自相关-偏自相关图（图4）可看出，自相关系数在滞后6步后呈拖尾状态，偏自相关系数在滞后4步后后呈拖尾状态，据此进行参数估计，在系数通过检验的条件下，初步选择AR(4)、ARMA(2,2)、ARMA(4,2)、ARMA(4,6)4种模型。

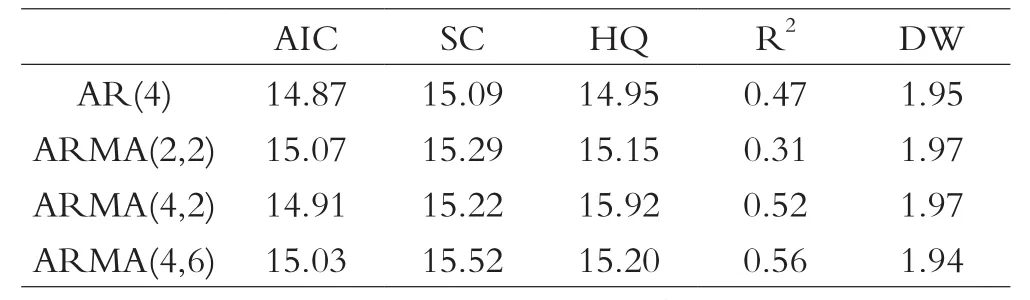
表1 4种模型的信息准则比较

通过对系数显著性检验（如表1所示），在信息准则越小，模型越佳的条件下，比较AIC、SC、HQ三种信息准则，最终确定AR（4）模型为最优模型。

（四）模型检验

对上述模型所生成的残差序列进行纯随机性检验，观察该序列所蕴含的信息是否被提取完全。由于其所有P值均大于0.05，接受原假设，说明该序列为白噪声序列，不蕴含历史信息，通过检验。

（五）残差自回归模型的对比

1.曲线拟合

在前文分析中可以得出，四川省GDP逐年增长，初步判断该项数据是关于时间的函数，使用SPSS软件对数据进行曲线拟合并寻找最佳拟合曲线。

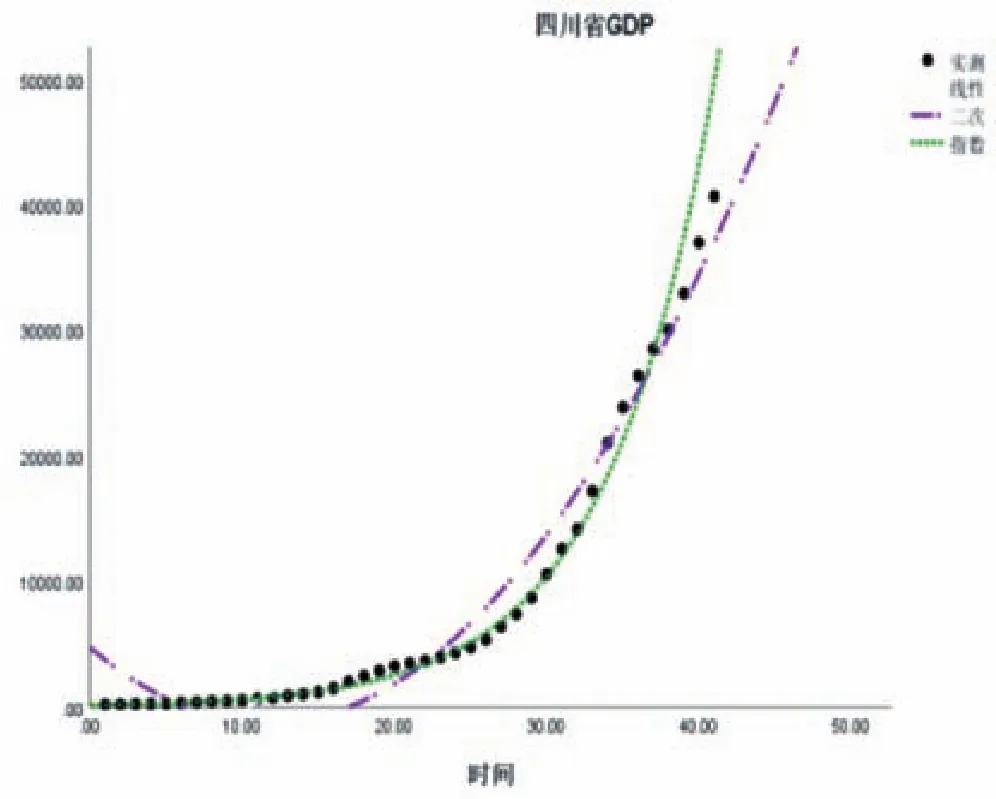
图5 GDP的曲线拟合图

从上图5中可以看出，指数曲线在前30年（1978-2008年）的时间里拟合度极高，但从2010年起拟合残差开始增大；二次曲线虽对前30年数据拟合度较低，却对后十年数据高度拟合，预测残差较小，故选取二次曲线对数据进行曲线拟合。

2.建立自回归模型

为了更好地分析与预测四川省GDP的增长趋势，现将拟合曲线与实际走势的残差进行修正。从拟合残差的自相关-偏自相关图（如图6所示）中可以看出，自相关系数正弦波动变化，呈拖尾状态，偏自相关系数在滞后2阶后迅速收敛为0，呈截尾状态，初步建立AR（1）、AR（2）模型，在通过对AIC信息准则以及拟合优度的比较，选择AR（2）模型，建立了二次曲线拟合后的残差AR（2）模型。

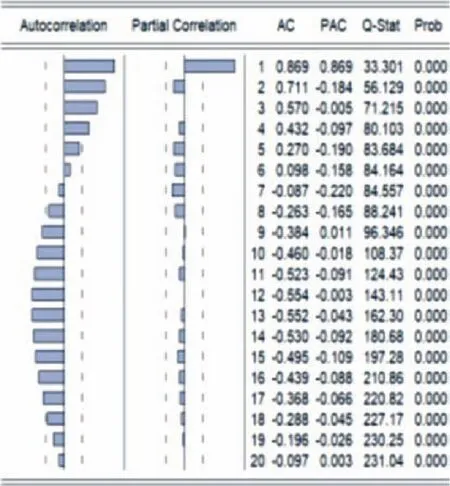
图6 拟合残差的自相关-偏自相关图

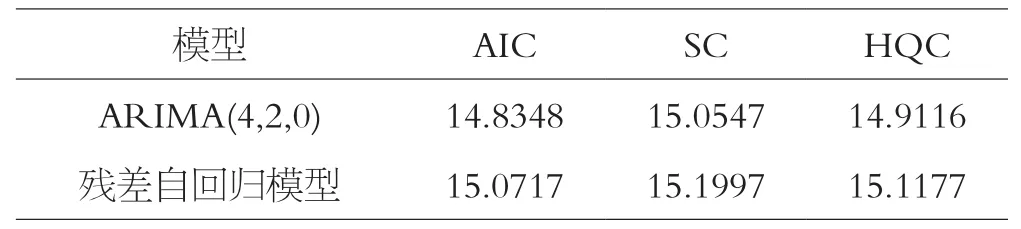
表2 ARlMA模型与残差自回归模型的对比

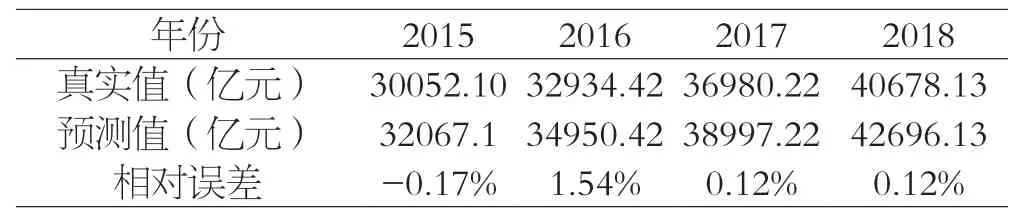
表3 2015-2018年四川省GDP的真实值与预测值对比

在两种模型均通过残差检验的基础上，进一步比较AIC等信息量，在信息量越小，模型越优的条件下，选取ARIMA（4，2，0）模型为最佳模型，再次证明ARIMA模型的可信度较高，现将模型书写如下：

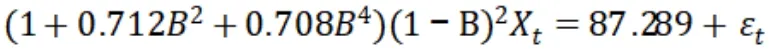
（六）模型预测

利用上述的ARIMA（4，2，0）模型对四川省2015-2018年的GDP序列进行预测，结果如表3所示，由上表3可知，2015-2018年的真实值与预测值的相对误差均小于5%，说明模型可以用于预测，且预测结果良好，但由于模型是对二阶差分后的GDP序列建立的，若用于长期预测的话，预测结果的精确性会有所下降。故仅对2019、2020年四川省GDP进行预测，分别为44454.64、48036.75亿元。

四、结论

从分析的数据来看，在改革开放前30年四川省GDP涨势迅猛，呈指数型增长，在遭遇了2008年全球金融危机及5·12特大地震之后，GDP呈二次函数型增长，涨势虽有回落，但也满足“稳中求进”的要求；从建立的模型来看，在AIC等信息准则的比较下，ARIMA（4，2，0）模型比残差AR（2）模型描述四川省GDP的增长规律更为精确，故采用ARIMA模型预计了2020年四川省GDP可达到48036.75亿元，可实现四川省政府在2016年的十三五工作会上提出的“到2020年地区生产总值比2010年翻一番以上”的目标。ARIMA（4，2，0）模型可为四川省政府在2020年制定宏观调控策略上提供一定的参考。