基于有限元的惯性导航系统动力学特性分析

刘 颖，董志娟，于 浩，杨 媛

(1.西安邮电大学 自动化学院，陕西 西安 710121； 2.吉林吉大通信设计院股份有限公司，吉林 长春 130012)

现代导航、制导、精确打击等领域对惯性导航系统在复杂环境下的可靠性和精度提出了越来越高的要求，而惯性导航系统的性能主要取决于其核心器件光纤陀螺组合[1-3]。理论上，单轴光纤陀螺对其轴向的振动敏感性较低，但由于零部件的装配、结构设计的缺陷等因素，导致光纤陀螺在振动和冲击环境下，精度变差，可靠性不高。因此，振动和冲击也成为影响惯性导航系统的关键因素之一，是高精度惯性导航系统应用中的一个主要问题，逐渐受到了国内外学者的重视和关注[4-7]。为了提高光纤陀螺在振动和冲击下的精度，国内外的学者们主要从器件设计[8]、误差补偿[9-10]、测试标定[11]和电路设计[12]等方面降低振动和冲击对光纤陀螺的影响，而关于改进结构设计和合理的装配工艺的研究相对较少[13]。

为了改善光纤陀螺对振动和冲击的敏感性，以光纤陀螺为核心的惯性导航系统为研究对象，研究光纤陀螺在振动和冲击下的变形的机理。采用有限元分析的理论，在基于各部件对结构刚度的影响大小的基础上，对惯导系统结构进行合理的简化，去除结构体上如垫片、沟槽、装配孔、突台和过渡圆角等细小特征。通过简化惯性导航系统模型，以期降低惯性导航系统对振动和冲击环境的敏感性，保证应用要求的精度和可靠性。

1 惯性导航系统模型

惯性导航系统是由光纤陀螺、加速度计、光源、线路板和机械支撑结构等若干零部件构成，其可靠性和精度主要由光纤陀螺的精度和可靠性决定。惯性导航系统的三维模型如图1所示。

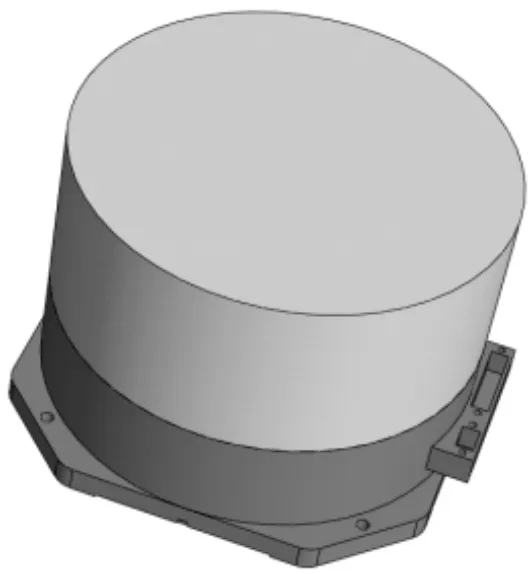
图1 惯性导航系统的三维模型

根据系统动力学原理[14]，具有n个自由度的离散化结构在任意激励f(t)作用下，其振动方程为

(1)

式中：M、C和K分别为结构质量矩阵、阻尼矩阵和刚度矩阵；x(t)为位移响应列向量。令系统的固有频率为fi，相应的正则主振型为Ψi，则存在

(2)

(3)

式中：I为单位矩阵；λi为系统第i阶特征值。

结构质量矩阵和刚度矩阵是系统各单元的特征矩阵，与结构的材料和形状有关。光纤陀螺组合材料有铝合金和环氧树脂材料，其材料性质如表1所示。

表1 材料性质

采用SolidWorks建立惯性导航系统的结构模型，在不影响模型准确的前提下，为了提高有限元模型的转化和分析效率、提高有限元模型的质量及保证有限元分析结果的精度，在基于各部件对结构刚度影响大小的基础上对惯导系统结构进行合理的简化，去除结构体上如垫片、沟槽、装配孔、突台和过渡圆角等细小特征。

将简化后的模型导入Ansys有限元分析软件进行有限元仿真。分别对惯性导航系统的零部件进行网格划分，薄板部分使用板壳单元；较厚的部位使用体单元；加速度计部件用质量元模拟；零件-零件的装配使用刚性杆单元(rigid bar element，RBE)2线刚性单元模拟。划分好的有限元模型如图2所示。有限元模型中共包含节点16 578个，单元12 438个，多点约束25个，单元性质集3个。

图2 惯性导航系统的有限元模型

按照惯性导航系统的使用环境进行边界条件的设定，对各个零部件的连接和接触类型进行设置。惯性导航系统与载体的连接是在螺孔的边缘采用螺钉固定的形式进行约束。

2 模态分析

模态分析是用来确定结构振动特性的一种技术，包括结构的自然频率、振型和振型参与系数，利用模态仿真可以求出其固有频率和与之对应的振动形态[15]。选用ANSYS软件对惯性导航系统进行模态分析，分别计算整个结构的前14阶模态的谐振频率，如表2所示。

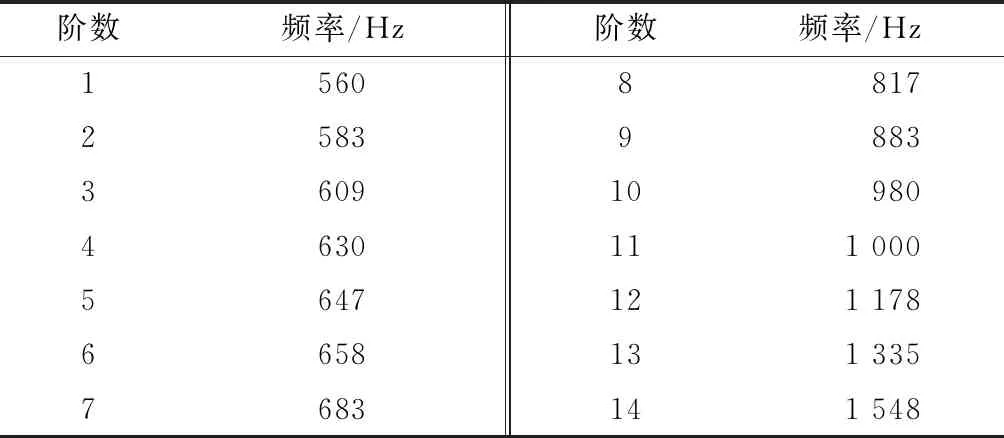
表2 惯性导航系统的固有频率

一般情况下，结构低阶的固有频率，或者某些特定阶的频率尤为重要，这是因为结构自身固有频率越小，越容易被人为的条件或者天然的条件所刺激。选取惯性导航系统中第1阶、第6阶、第11阶、第14阶等4个较容易产生形变的阶数进行相应的模态分析，如图3所示。

图3 不同阶数模态

由图3可知，第11阶之前均为不重要的局部频率，惯性导航系统主体结构的频率高于第11阶的1 000 Hz，结构的整体刚度较大。惯性导航系统的核心部件是惯性测量单元安装结构的固有频率也高于1 000 Hz，在实际使用过程中，不易受外界环境的影响。

获取了惯性导航系统的固有频率和模态分析结果之后，可进一步研究整体结构在承受随机载荷下的受载情况。惯性导航系统的模态分析结果受多方面因素的影响，例如结构件有限元模型的复杂度、连接件的接触类型设置、拟合的精确度以及边界条件的设定等。但是，分析结果在很大程度上能够反应实际应用情况，可以对结构设计及随机振动分析起到重要参考作用。

3 随机振动分析

为了分析工作时振动对惯性系统的影响，故对惯性导航系统进行随机振动分析。随机振动分析是一种基于概率统计学理论的谱分析技术，也被称为功率谱密度分析[16]。

从概率统计学的角度出发，将时间历程的振动和冲击转变为功率谱密度(power spectral density，PSD)加速度载荷，通过PSD反应随机激励的输入特征，进而进行随机振动分析，得到不同频率所对应的功率谱密度，数值如表3所示。总均方根加速度为16.93 grms。

表3 加速度PSD载荷

加速计、光纤陀螺、惯性导航系统箱体和线路板等4个关键部位在x工况加速度功率谱密度响应如图4所示。

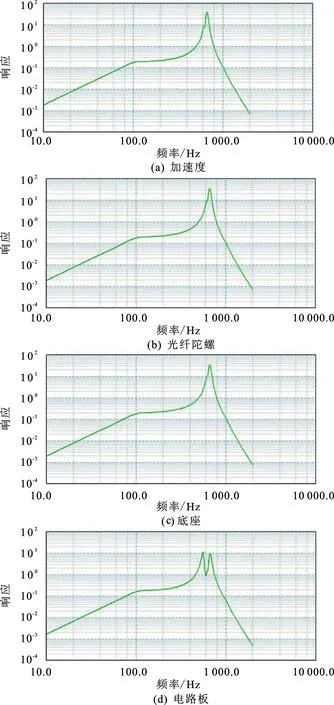
图4 4个关键部位在x工况加速度PSD响应

加速计、光纤陀螺、惯性导航系统底座和线路板等4个关键部位在y工况加速度功率谱密度响应如图5所示。

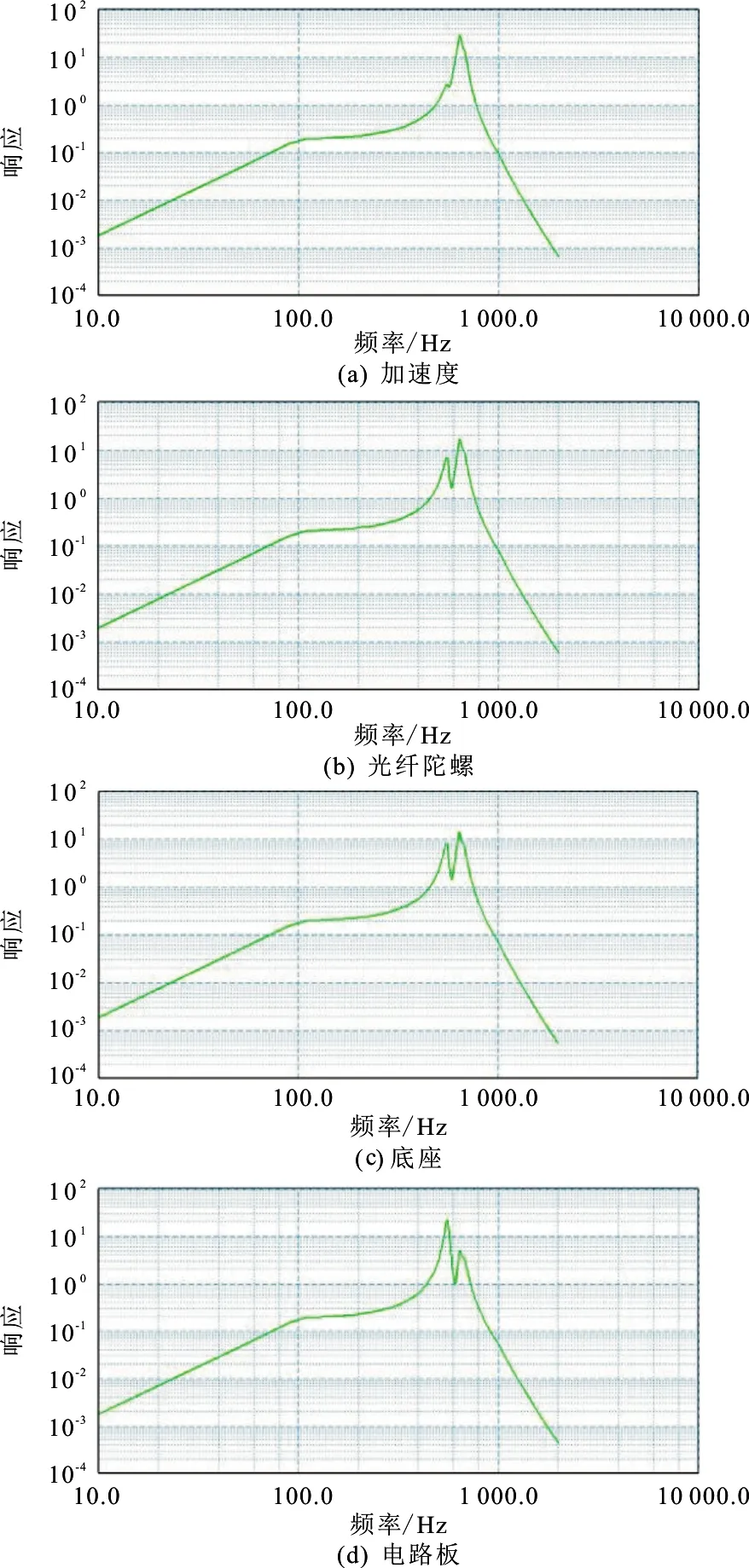
图5 4个关键部位在y工况加速度功率谱密度响应

由图4和图5可以看出，根据输入条件，有限元分析的惯性导航系统结构在x方向PSD激励下，陀螺的最大加速度响应总均方根值为52.06，加速度计的功率谱密度响应值为42.87、陀螺的功率谱密度响应值为45.69、陀螺座的功率谱密度响应值为34.58、箱体的功率谱密度响应值为33.62、电路板的功率谱密度响应值为35.24。在y方向PSD激励下，陀螺的最大加速度响应总均方根值为47.96，加速度计的功率谱密度响应值为43.62、陀螺的功率谱密度响应值为47.10、陀螺座的功率谱密度响应值为32.45、箱体的功率谱密度响应值为31.32、电路板的功率谱密度响应值为36.32。由此可得，惯性导航结构在复杂随机振动环境下可以保证其可靠性和精度。

4 结语

为了保证惯性导航系统在复杂振动环境下正常可靠的工作，建立了其三维模型和有限元模型，通过设定要求的边界条件和约束条件，分析系统内部关键元器件及组件的固有频率、变形量及复杂振动环境的响应，然后采用基于有限元的方法对结构装配体进行了模态和随机振动分析。分析结果表明，惯导系统的局部频率偏低，但结构主体部分的固有频率高于1 000 Hz，结构整体的刚度较大。从结构关键部位结构最大加速度响应总均方根和加速度响应放大倍率可知，惯性导航结构在复杂随机振动环境下可以保证其可靠性和精度，在振动环境下工作安全可靠，不会影响惯性测量单元的测量精度。