一种改进的HSPCNN图像分割算法

田小平，赵怡雪，吴成茂

(西安邮电大学 电子工程学院，陕西 西安 710121)

图像分割是图像识别和机器视觉领域的基本技术，根据图像像素之间的相似性或非连续性策略将图像分割成多个区域，分割质量的好坏直接影响后续图像处理的效果[1-3]。现有的图像分割方法有基于阈值、区域、边缘检测和特定理论的分割[4-5]。在基于特定理论的图像分割中，基于神经网络的图像分割利用神经网络更易引入邻域信息的优势，解决了图像存在噪声和不均匀问题。脉冲耦合神经网络(pulse coupled neural network，PCNN)作为第三代人工神经网络，更好地模仿了神经元脉冲耦合、时空累加和不应期特性，且无需训练便可直接应用，故基于PCNN的图像分割在基于神经网络的图像分割算法中表现优越[6]。

通常情况下，PCNN需要根据经验设定参数且其只能完成二值分割任务[7]，而简化脉冲耦合神经网络(simplified pulse coupled neural network，SPCNN)模型可自适应设定参数且能够实现多层次分割，但其停止迭代条件以点火率为基准，泛化能力有限[8]。利用不同神经元在结构和连接上的差异，将3个不同结构的SPCNN以不同参数连接形成异构简化脉冲耦合神经网络(heterogeneous simplified pulse coupled neural network,HSPCNN)模型，该模型的停止迭代条件以最大熵为基准，与SPCNN模型相比泛化能力有所提升，但该模型分割图像的效果取决于阈值向量的设定[9]。

阈值分割的核心在于以一定准则快速寻找最优分割阈值，采用穷举搜索法寻优，计算量大、分割时间长。将阈值选取问题视为以准则函数为目标函数的优化问题,并借鉴群智能算法则可提高优化效率[10]。其中，粒子群(particle swarm optimization，PSO)算法因其原理简单、参数较少以及能快速收敛至最优解等优点，被广泛应用。

以阈值为优化目标的准则函数构造是一个难点。采用单一评价准则设定阈值，分割效果不理想[11-14]。将交叉熵评价参数、边缘匹配评价参数及噪点评价参数的加权函数作为PSO的综合评价准则可实现PCNN自动分割[15]，但因评价参数的归一化方式不同，交叉熵的值得不到保证，会产生分割无效现象。因此，针对文献[15]仅能完成二值分割任务和评价准则不完善的问题，在该评价准则的基础上引入信息熵评价参数，并通过PSO优化技术将改进的综合评价准则用于评价HSPCNN分割图像，以期提升HSPCNN图像自动分割算法的泛化能力。

1 基础理论概述

1.1 HSPCNN图像分割算法

HSPCNN由不同结构的SPCNN以不同参数连接形成，HSPCNN结构示意图如图1所示。

图1 HSPCNN结构

SPCNN中的神经元对应图像中的像素，神经网络对应图像分割,则HSPCNN的数学模型可描述为

(1)

U1,ij(n)=e-afU1,ij(n-1)+u1,ij(n-1)，

(2)

U2,ij(n)=e-afU2,ij(n-1)+u2,ij(n-1)+SijL12，

(3)

U3,ij(n)=e-afU3,ij(n-1)+u3,ij(n-1)+SijL23，

(4)

um,ij(n-1)=Sij[1+βmLm,kl(n-1)]，

(5)

Em,ij(n)=e-aeEm,ij(n-1)+VEYm,ij(n)，

(6)

(7)

(8)

式中，i、j、k和l分别代表像素位置，Sij代表像素灰度值，n代表迭代次数。βm、Wij,kl(m)、Lm,ij、Um,ij、Em,ij和Ym,ij分别代表SPCNN单元的连接强度、连接权重矩阵、连接输入、内部活动项、阈值和输出，m为SPCNN单元的标签，取值1,2,3。VL和VE分别代表迭代过程中Lm,ij和Em,ij的放大系数，af和ae分别代表迭代过程中Um,ij和Em,ij的衰减常数，L12和L23代表异构连接权值。

神经元兴奋有强弱，故输出不应只有点火和静默两种状态。为使网络对不同输入有不同响应，将m个SPCNN单元的输出累加。Ym,ij表示第m个SPCNN单元的输出，am表示神经元点火时输出的脉冲高度。设定am满足的条件为a1≠a2≠a3、a1,a2,a3∈(0,1)、a1+a2+a3=1,当a1=0.3，a2=0.5，a3=0.2时,HSPCNN输出的分割图像Y(n)∈(0,0.2,0.3,0.5,0.7,0.8,1)[9]，故该模型理论上分割类别最多可以分7类。

1.2 PSO优化算法

PSO是一种模仿鸟群捕食行为的群智能算法。假设粒子群数目为B，粒子群最大进化代数为g，粒子携带d维信息。以粒子i的d维信息为自变量构造适应度函数，每个粒子通过适应度函数都对应一个适应值[16-17]。在粒子进化过程中，保留适应值大的粒子为个体最优pbestid，保留所有pbestid中适应值最大的粒子为全局最优gbestid。粒子通过认知因子c1、随机数r1以及上一次位置与pbestid距离得到自身经验

X1(g)=c1r1[pbestid(g)-Xid(g)]。

(9)

通过社会因子c2、随机数r2以及上一次位置与gbestid距离得到社会经验

X2(g)=c2r2[gbestid(g)-Xid(g)]。

(10)

由权重w、上一次速度Vid(g)、式(9)和式(10)可得到当前速度的计算表达式为

Vid(g+1)=wVid(g)+X1(g)+X2(g)。

(11)

根据上一次位置Xid(g)和式(11)，得到位置更新的计算表达式为

Xid(g+1)=Xid(g)+Vid(g+1)。

(12)

自然变异即对某些变量以一定概率重新初始化。在PSO算法中引入自然变异操作，即在更新后的粒子中以一定概率加入重新初始化的粒子，使粒子跳出先前搜索到的最优位置以避免陷入局部最优。然后将所有粒子的适应度值与pbestid的适应值和gbestid的适应值进行比较，如果更优则将其作为pbestid和gbestid。

2 PHSPCNNM图像分割

2.1 改进的综合评价准则

1)交叉熵评价参数

交叉熵衡量源图像和分割图像的差异，交叉熵越小，分割图像效果越好。交叉熵定义为

C(t)=C1(t)+C2(t)，

(13)

式中：t为灰度阈值，t∈[0，255]；f为图像灰度值；h(f)为图像的灰度直方图；u1(t)和u2(t)分别为背景和目标的类内均值;Z为源图像的灰度上限,交叉熵归一化处理后得到的评价交叉熵优劣参数为

(14)

D取值范围为(0,1)，D越接近1，分割阈值越优，分割越准确。

2)边缘匹配评价参数

利用边缘引导神经元同步发放脉冲，将目标及其纹理细节逐一分割。采用最大类间方差法获取阈值并采用canny算子进行边缘检测。边缘匹配评价参数为分割图像边缘像素与源图像边缘像素的重合数目占源图像总边缘像素数目的比例，定义为

(15)

式中，Sedge(i,j)和Yedge(i,j)分别为源图像和分割图像的二值化边缘。Q取值范围为(0,1)，Q越接近1，分割图像边缘与源图像边缘重合度越高，分割图像轮廓及纹理细节保留越好。

3)噪点评价参数

若目标像素8-邻域范围内无其他目标像素，则将其视为盐噪点；若背景像素8-邻域范围内无其他背景像素，则将其视为椒噪点。各分割图像累加所得实际分割图像的噪点评价参数定义为

(16)

当Ym(i,j)=am时，Ym(i,j)为目标像素；当Ym(i,j)=0时，Ym(i,j)为背景像素。Vm(i,j)代表中心像素Ym(i,j)与其8邻域像素的和，Smapm为盐点标记图，Pmapm为椒点标记图，K为图像像素总数，Nm为各分割图像的噪点评价参数。N取值范围为(0,1)，N越接近1，实际分割图像受噪点影响越小。

4)信息熵评价参数

信息熵描述灰度图像空间分布，信息熵越大，分割图像包含信息越多。为得到包含更多信息的分割图像，定义基于粒子群的信息熵评价参数为

(17)

其中：HS代表实际分割图像的熵；HL代表分割类别为7类时分割图像的最大熵。

因为实际分割类别不一定为7类，为此修正信息熵评价参数为

(18)

其中，HZ代表由HSPCNN模型和图像本身决定的真实分割的类数所对应的最大熵。H取值范围为(0,1)，H越接近1，分割图像从源图像得到信息量越大，分割图像细节越丰富。

为正确分割目标和背景，并兼顾目标整体轮廓和纹理细节，通过引入信息熵评价参数改进综合评价准则，可表示为

M=w1H+w2D+w3Q+w4N。

(19)

式中，w1、w2、w3和w4分别表示式(18)、式(14)、式(15)和式(16)的权重。对于特定图像，基于信息熵的阈值分割和基于交叉熵的阈值分割存在一个更适用的问题且信息熵评价参数和交叉熵评价参数的归一化方式相差较大，故w1和w2的取值有所偏重。保持轮廓与不因分割产生噪点同样重要且边缘匹配评价参数与噪点评价参数归一化方式都相对精确，故w3和w4取值大致相同。w3和w4应与w1和w2中较大者保持一致，具体权重向量应根据具体图像灵活设定。

2.2 PHSPCNNM算法

PHSPCNNM算法将改进的综合评价准则式(19)作为粒子群的适应度函数，通过粒子群优化算法对图像进行分割。具体步骤如下。

步骤1初始化粒子群，包括粒子数目、最大进化代数、随机速度和随机位置。将粒子数目B设为5，最大进化代数g设为100。

步骤2以HSPCNN算法的阈值向量T=[E1,ij(0),E2,ij(0),E3,ij(0)]为优化目标，将HSPCNN迭代次数n设为1，利用式(19)评价每个粒子的适应度，初始化pbestid和gbestid。

步骤3更新每个粒子的速度与位置。因需要计算交叉熵，故灰度阈值E1,ij(0)、E2,ij(0)和E3,ij(0)的取值范围均为[0,255]。若寻优跳出边界，则在[0,255]范围内为T重新取随机值。

步骤4加入自然变异，更新pbestid和gbestid。

步骤5算法的终止条件设置为达到设定迭代次数100、超过设定运行时间10 min或10代以内的适应值误差小于预设误差10-6。若满足以上任一退出条件，则退出程序，输出最优阈值向量和最优分割图像，否则返回步骤3，继续更新阈值向量T和分割图像。

3 实验结果及分析

为了验证算法可靠性，在Matlab R2018a实验平台下，对伯克利(Berkeley)分割数据集中9幅图进行分割实验。针对#3096、#15088、#143090、#219090、#227092、#241004和#253055等7幅图，将权重向量设定为(2.66,2,2.66,2.66)，针对#62096和#102061两幅图，将权重向量设定为(2,2.66,2.66,2.66)。

将最大熵、最小交叉熵、现有综合评价准则以及改进的综合评价准则作为HSPCNN分割图像的适应度函数，给出基于粒子群和最大熵的HSPCNN(HSPCNN based on PSO and maximum entropy,PHSPCNNH)算法、基于粒子群和最小交叉熵的HSPCNN(HSPCNN based on PSO and minimum cross entropy,PHSPCNND)算法、基于粒子群和现有综合评价的HSPCNN(HSPCNN based on PSO and existing comprehensive evaluation,PHSPCNNC)算法、基于粒子群和改进综合评价的HSPCNN(HSPCNN based on PSO and improved comprehensive evaluation,PHSPCNNM)算法。分别利用HSPCNN算法、PHSPCNNH算法、PHSPCNND算法、PHSPCNNC算法和PHSPCNNM算法对图#3096、 #62096、#241004和#253055进行分割，结果分别如图2-图5所示。

图2 不同算法对图#3096的分割结果

图3 不同算法对图#62096的分割结果

图4 不同算法对图#241004的分割结果

图5 不同算法对图#253055的分割结果

由图2-图5可以看出，HSPCNN算法无法完整地分割出目标，PHSPCNNH算法存在错分现象，PHSPCNND算法丢失大量细节，PHSPCNNC会产生分割无效现象，而PHSPCNNM在纹理细节处理方面更出色。

以改进的综合评价准则、峰值信噪比及误分率为指标，验证PHSPCNNM算法性能。不同算法的综合评价参数对比分别如表1-表4所示。

表1 不同算法对图#3096的综合评价参数对比

表2 不同算法对图#62096的综合评价参数对比

表3 不同算法对图#241004的综合评价参数对比

表4 不同算法对图#253055的综合评价参数对比

从表1-表4的评价准则数据可以看出，PHSPCNNM算法在评价参数对比中表现稳定且优于其他算法。

在评价准则的基础上添加峰值信噪比[18]及误分率[19]作为评价分割优劣的参考，不同算法的峰值信噪比及误分率对比分别如表5-表8所示。

表5 不同算法对图#3096的峰值信噪比及误分率对比

表6 不同算法对图#62096的峰值信噪比及误分率对比

表7 不同算法对图#241004的峰值信噪比及误分率对比

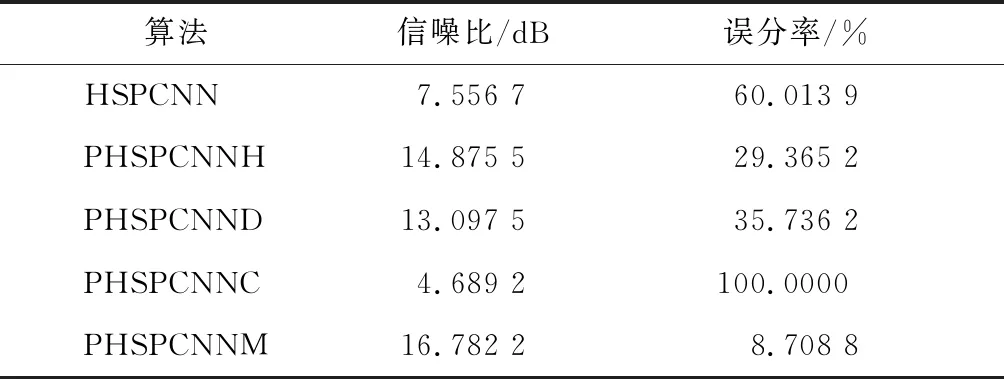
表8 不同算法对图#253055的峰值信噪比及误分率对比

从表5-表8可以看出，PHSPCNNM算法具有更高的峰值信噪比和更低的误分率。

为了验证PHSPCNNM算法的有效性和可靠性，对大量图像进行了分割实验，部分实验结果分别如图6-图10所示。可以看出，对于不同场景的图像，PHSPCNNM算法都能稳定正确的分割出目标与背景，并兼顾其轮廓和纹理细节。

图6 不同算法对图#143090的分割结果

图7 不同算法对图#219090的分割结果

图8 不同算法对图#15088的分割结果

图9 不同算法对图#227092的分割结果

图10 不同算法对图#102061的分割结果

4 结语

结合粒子群和综合评价准则的改进HSPCNN图像分割算法，以阈值向量为优化目标，通过引入信息熵评价参数改进现有综合评价准则，然后将改进综合评价准则作为PSO的适应度函数，通过PSO寻优得到了更稳定、更理想的分割图像。实验结果表明，改进的HSPCNN图像分割算法在目标整体轮廓、纹理细节保持方面更出色，抗噪能力更强。此外，该算法的综合评价参数、峰值信噪比和误分率均为最优。