一种模式可配置的单精度浮点乘法器设计

蒋 林，田 璞，邓军勇

(1.西安邮电大学，电子工程学院，陕西 西安 710121； 2.西安科技大学，集成电路实验室，陕西 西安 710054)

计算机处理器需要处理大量的乘法运算，由于乘法运算的复杂度较高，所以，乘法器的运算速度和功耗通常也就决定了处理器的运行速度和功耗[1]。单精度浮点乘法器采用两个符合IEEE754标准的浮点数完成乘法运算，与定点运算相比，浮点运算单元(floating point units,FPUs)提供了高精度、高动态范围的实际值以及简单的编程模型[2]。

一般而言，频率、功耗和面积是衡量乘法器和处理器性能的3个重要指标。为了降低浮点乘法器功耗，大多数的设计都是通过牺牲计算的精度来实现的[3-4]。例如，在某些对精度要求不高的机器学习和数据传感技术中，有研究直接利用一个乘数的值来代替乘法的结果，以降低功耗[5]，但是，该方法的误差较大。在对运算精度和速度比较高的应用如信号处理、神经网络和流处理等应用[6-7]中，为提高计算速度，有研究通过重构流水线级数的方式来提高运算频率[8]，这会增大设计面积开销。为了降低浮点乘法的面积开销，使用改进的Booth编码，调整扩展位的位置可以有效减少版图面积[9]，但是，这种设计会增加浮点乘法运算的功耗。

单精度浮点乘法器的关键技术主要在尾数乘法的设计部分，该部分通常由定点数乘法实现。传统的定点数乘法算法有原码一位乘法、Booth算法和Wallace树型结构。原码一位乘法基本思想是“判断—加法—右移”循环，实现简单，功耗小，但是，该算法的实现频率低。Booth算法是对原码一位乘法的改进，每次判断右移的尾数为两位，其实现的周期数几乎是原码一位乘法的一半，但是这种算法功耗较大[10]。Wallace结构在乘法器设计中采用树型结构，减少了关键路径和所需的加法单元数目，但是，这种方法会增加功耗和面积[11]。目前的设计更多地关注某一个单个性能，难以兼顾对频率、面积和功耗的需求。

针对以上方法的不足，拟设计一种模式可配置单精度浮点乘法器。利用互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS)工艺设计原码一位、基4-Booth和Wallace树型算法3种常用定点数乘法的浮点乘法器，并且测试这3种乘法器的性能。在乘法器的尾数乘法部分添加模式选择模块，根据应用场景对频率、功耗和面积3个性能的不同需求选择和切换相应的算法，以满足不同应用对处理器性能的要求。

1 单精度浮点乘法器

浮点乘法器通过A和B两个操作数的符号位进行异或操作来计算C=A×B的符号位，其将指数项的有效值相加，并将两个尾数相乘得到结果的尾数。浮点乘法器的原理示意图如图1所示。

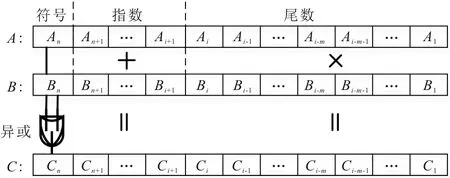
图1 浮点乘法器原理示意图

单精度浮点乘法器的操作数符合IEEE754标准。这种表示方式可以使数据的精度更高，表示范围更大。具体的精度浮点数格式示意图如图2。其中，最高位s表示符号位，阶码e表示第23-30位，尾数f表示第0-22位。尾数用原码表示，第一位总是1，可以在尾数省略第一位的1，称为隐藏位，因而单精度格式的23位尾数实际是24位有效数字。

图2 精度浮点数格式示意图

单精度浮点乘法器的关键计算模块就是尾数乘法部分，这部分通常通过定点数乘法实现，常见的定点数乘法有原码一位乘法、Booth算法[11]和Wallace树型结构[9]。

原码一位乘法的原理示意图如图3所示。经过n次的“判断—加法—右移”循环，直到输出乘积，但随着操作数位宽的增加原码一位乘法循环的次数会增加，即图中右移的次数会增加，导致较低的计算频率。

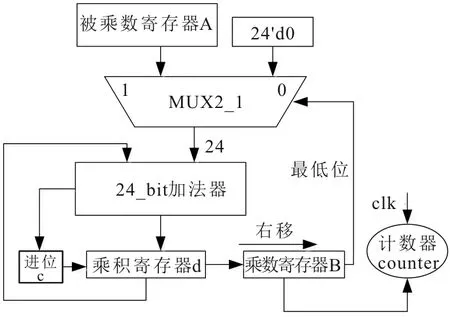
图3 原码一位乘法原理

基4-Booth乘法[11]原理示意图如图4所示。基4-Booth乘法是对原码一位乘法的改进，其每次右移的位数是两位。基4-Booth乘法一定程度上减少了计算周期数，图4中控制逻辑的计数器比原码一位乘法复杂，会造成更大的功耗。

图4 基4-Booth乘法原理

Wallace结构的乘法器在设计中采用树型结构[9]，一种常用的6:4进位保存加法器(carry save adder,CSA)的Wallace树型结构乘法器原理示意图如图5所示。Wallace树型6:4CSA压缩器能够减少关键路径和所需的加法器单元数目，同时也提高了计算频率，但是，这会造成较大的能量消耗和面积，另外，由于每个计算单元的计算量会增大，从而增大了布线资源消耗。

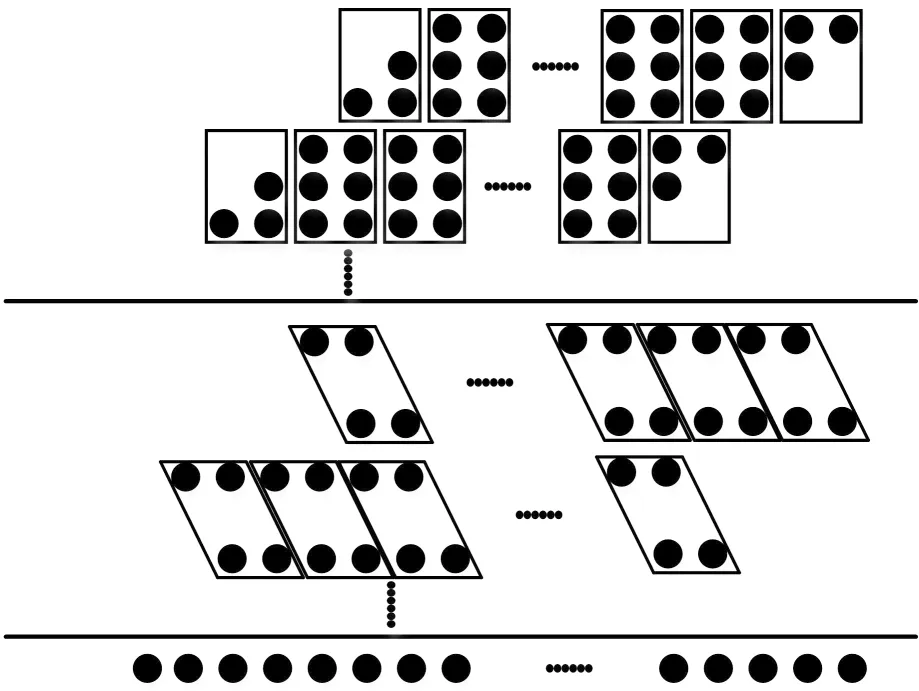
图5 6:4CSA压缩器的Wallace树型结构

不同的应用领域对处理器性能要求各不相同。例如，在电子产品等应用领域，对功耗有较高的要求。在视频图像处理领域，由于对海量图像数据处理的实时性要求越来越高，就需要低功耗且占用面积小的浮点乘法运算。传统的乘法算法无法同时兼顾面积、频率和功耗。

2 多模式浮点乘法器设计

提出一种模式可配置的浮点乘法器，根据不同应用领域对性能的不同需求以及3种定点数乘法算法在频率、面积和功耗方面的优势，配置对应的标志位，选择相应的乘法算法实现浮点乘法运算。

2.1 乘法器整体框架

设计的可配置浮点乘法器包括符号异或模块、指数加模块、判断模块、尾数乘法模块和尾数规格化及舍入模块，其结构示意图如图6所示。

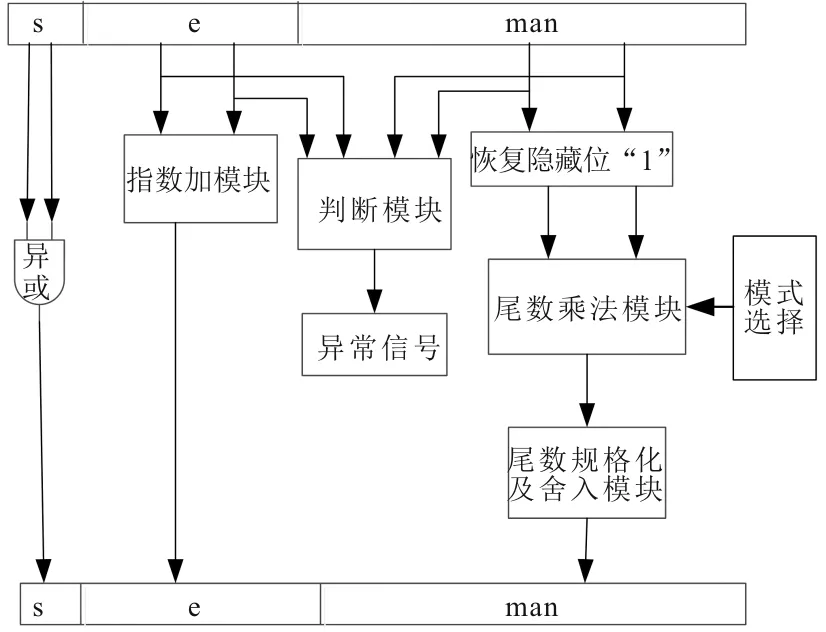
图6 可配置浮点乘法器结构图

单精度浮点乘法器的实现过程包括如下5个步骤。

步骤1将32位的浮点数分段，分别为符号位、指数位和尾数，同时恢复尾数的隐藏位“1”。

步骤2对符号位进行异或操作。

步骤3将阶码(指数)相加，尾数相乘。

步骤4对尾数进行规格化和舍入操作，然后判断阶码是否有溢出。

步骤5将计算的符号位、阶码和尾数进行拼接并作为结果输出。

2.2 模式选择的可重构设计

浮点乘法运算的尾数乘法采用定点数乘法。尾数乘法部分一般采用原码一位乘法、基4-Booth算法和Wallace树型算法3种定点数乘法算法实现。利用90 nm CMOS工艺设计了基于这3种定点数乘法算法的浮点乘法器，并且完成逻辑综合(design compiler,DC)，3种算法的浮点乘法器性能测试结果如表1所示。

表1 3种浮点乘法器性能测试结果

可以看出，原码一位乘法在面积和功耗方面具有优势，当应用场景对面积和功耗要求较高时，采用原码一位乘法是较好的选择。Wallace树型算法在延时(即频率)性能较好，当应用场景对延时/频率有较高要求时，应该选择Wallace树型算法。

根据表1中的性能测试结果，进而设计了可配置浮点乘法器的面积最优模式、频率最优模式和功耗最优模式3种计算模式，具体的模式及其算法选择如表2所示。

表2 模式及实现算法

可配置的单精度浮点乘法器的设计思路是在尾数乘法部分添加了模式选择模块，根据不同应用对延时、功耗和面积3个性能的需求在原码一位乘法和Wallace 树型算法之间进行选择和切换，以满足不同应用对处理器性能的要求。

1)面积、功耗最优模式

当应用对乘法器面积要求较高时，电路的标志位模式切换至“00”，当应用对乘法器功耗要求较高时，模式切换至“01”，选择在面积和功耗方面有优势的原码一位乘法算法实现浮点乘法运算。面积或功耗最优浮点乘法原理示意图如图7所示。

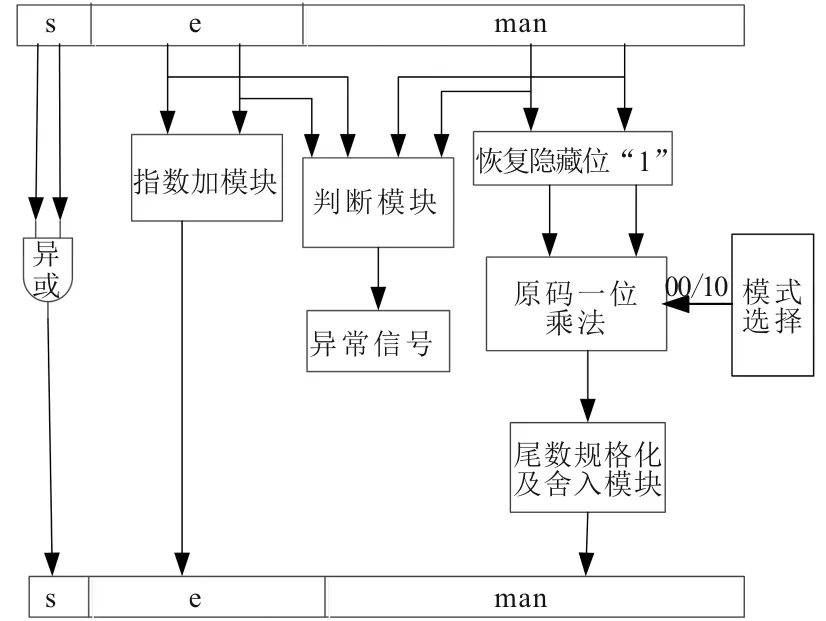
图7 面积或功耗最优浮点乘法原理

2)频率最优模式

在数字信号处理等应用中，对浮点运算单元的频率要求较高，电路的标志位模式切换至“01”，选择频率较优的Wallace树型算法来实现浮点乘法。频率最优浮点乘法原理示意图如图8所示。

图8 频率最优浮点乘法原理

3 实验结果及分析

在ModelSim SE-6410.1c上实现功能仿真，仿真结果表明，设计的可配置浮点乘法器计算一次浮点乘法运算最多需要23个时钟周期，最少需要7个时钟周期，平均需要15个时钟周期。和文献[12]的粗粒度可重构处理器实现的浮点乘法器相比，所需周期个数平均降低了87.3%。对比结果如表3所示。

表3 与文献[12]对比

为评估所提出的模式可配置单精度浮点乘法器，在90 nm CMOS工艺上做了逻辑综合，其中面积、延时和功耗的结果如表4所示，综合结果表明，与文献[2]的ifpmul32相比，延时和功耗均有所降低，最小延时降低了57%，最小面积降低了76.6%。

表4 与文献[2]对比

4 结语

针对现有单精度浮点乘法器不能兼顾不同应用领域对频率、面积和功耗的需求，提出了一种模式可配置浮点乘法器。利用CMOS工艺设计原码一位乘法、基4-Booth算法和Wallace树型算法3种常用定点数乘法的浮点乘法器，并且测试其性能。在乘法器的尾数乘法部分添加模式选择模块，根据应用场景对频率、功耗和面积3个性能的不同需求选择和切换相应的算法，以满足不同应用对对处理器性能的要求。实验结果表明，设计方案能够根据应用场景实现不同算法之间的切换，且性能较好。