全钒液流电池建模与流量特性分析

2020-04-04邵军康莫言青董学平朱浩宇

储能科学与技术 2020年2期

邵军康，李鑫，莫言青，邱亚，董学平，朱浩宇

（合肥工业大学电气与自动化工程学院，安徽合肥 230009）

随着储能技术的快速发展以及环境保护观念日益深入人心，全钒液流电池（vanadium redox flow battery,VRB）因其长寿命、高安全等特点而得到了越来越广泛的应用。VRB储能系统具有广阔的应用前景和巨大的潜在市场，在工业化的进程中，已经建设了各类大容量VRB储能系统示范应用工程。

建立精准且全面的VRB模型是实现VRB推广应用的一个前提条件，也是实现最优流量控制的基础。根据构建原理将VRB模型分为电化学模型、等效电路模型及混合电路模型三大类[1]。对于电化学模型的研究，Tang等[2-3]考虑了自放电反应中各种因素，健全了电化学自放电反应的数学模型，研究了使用不同的离子隔膜条件下离子浓度和容量的变化，建立了离子扩散作用的数学模型，分析了充放电电流大小及隔膜扩散系数对离子浓度变化的影响。Skyllas-Kazacos等[2]研究在不同外加电流且SOC达到50%的条件下进行充放电，测试电池输出电压，结果表明输出电压与外加电流成线性关系。Chahwan等[5]建立的电化学数学模型是关于电压与SOC的关联方程。Shah等[6-7]结合涉及钒物质反应的全局动力学模型，通过综合描述将复杂系统进行简化计算，建立了电池二维数值模型，但计算时忽略了温度变化（特别是热损失）可能会发挥的重要作用。田野等[8]对二维模型进行改进建立了更为全面的三维模型，建模时考虑了流场、浓度场以及温度场，针对流场特性、钒离子的浓度分布以及温度变化情况进行模拟研究，但忽略了膜发热引起的温度变化，故温度场计算不准确。对于等效电路模型，Chahwan[9]提出了等效损耗电路模型，文献[10-13]分别推导了5 kW·h、10 kW·h、20 kW·h、40 kW·h、500 kW·h等不同功率、不同容量等级的VRB仿真模型。文献[14]在常见的VRB系统等效损耗模型基础上考虑离子扩散的作用，该模型可以表征电池的离子浓度动态变化情况，但没有将电堆和储液罐中的钒离子区别开来。而建立一个全面的VRB系统需要考虑电化学反应、流体力学、电路控制、电解液温度变化等方面。文献[15]根据钒电池基本原理和等效损耗建立了等效电路模型，根据机械损耗和钒电池结构参数建立钒电池流体力学模型，并将流体力学模型与等效电路模型结合。关于流量控制的研究，文献[16]研究了流量对VRB系统效率的影响，根据电化学模型和机械模型对电解液的流量进行了分析，但模型无法体现VRB的电学性能。

本文在等效电路模型基础上增加了流体力学模型和电化学模型，给出了更加全面展现VRB相关特性的混合模型，该模型可区分储液罐和电堆中各价钒离子浓度，即实时跟踪储液罐中钒离子浓度变化计算出运行时的SOC值，又可根据电堆中钒离子浓度计算出堆栈电压Us，实现堆罐分离。

通过对VRB混合模型的分析，发现充放电期间的最优流量是关于荷电状态的函数，并通过仿真分析，得到不同SOC状态下的最优流量值，根据该现象利用流量随着荷电状态SOC的变化进行分段控制，有效地提高了系统效率。

1 全钒液流电池结构与工作原理

全钒液流电池系统结构主要由电堆、两个独立正/负储液罐、循环泵以及管道等模块组成，钒电解液储存于储液罐和电堆中。电堆由多片单体电池串联组成，单体电池主要由离子交换膜、电极、双极板、液流框板、密封件构成，单片单体电池内的正、负极电解液用离子交换膜隔开。钒电解液以四种钒离子溶液的形式存在，正极电解液为活性电对蓝色的VO2+和黄色的VO2+，负极电解液为活性电对紫色的V2+和绿色的V3+。另外，电堆外接负载或电源，循环泵以及管道连接电堆和储液罐。

外接电源启动对VRB进行充电时，钒离子在电堆中电极发生充放电氧化还原反应，正极VO2+不断的失去电子逐渐氧化成VO2+，电子通过电路到达负极，负极V3+得到电子逐渐被还原为V2+，并且在循环泵压力作用下，储液罐中的钒电解液流进电堆，均匀流过各单体，持续进行反应。接入负载VRB放电时，正极的VO2+得到电子被还原为VO2+，同时，负极的V2+不断失去电子氧化为V3+。离子交换膜只允许氢离子通过，来平衡电池内部的电荷。即充电时V3+和VO2+离子浓度逐渐减小，V2+和VO2+增大，放电时相反。其中，电极反应为：

正极充放电

负极充放电

总反应

由于各价钒离子存在浓度差，在实际运行中电堆会发生交叉自放电反应，如式（4）～（7）所示。

正极交叉放电

负极交叉放电

2 全钒液流电池混合模型

本文根据全钒液流电池的组成和工作原理，建立了在等效损耗模型基础上考虑了电化学因素和流体力学因素的混合模型。为了简化，对模型做出以下规定：

（1）温度是恒定的，在298 K下；

（2）电解液体积在正电解液和负电解液中保持一致；

（3）电解液在储槽和电堆内瞬间混合，并均匀分布；

（4）产生氢的副反应可以忽略不计；

（5）基于等效原理，模型参数适用于所有对应的单体。

2.1 等效损耗电路模块

VRB的等效损耗电路模块如图2所示。

Chahwan等[5]提出了等效损耗电路模型。内部电阻包括欧姆内阻Rb和反应内阻Ra，固定的寄生电阻Rf为系统控制器和堆栈旁路电流引起的损耗内阻。可变泵损电流Ip由循环泵引起的损耗电流。电极电容Ce反映电池充放电时的瞬态性能。Us表征堆栈电压（即开路电压，OCV），Ud是电池端电压，Id是充放电电流，Is是流经堆栈的电流，Ie是电容的电流，各种电流参考方向如图2所示。

2.2 电化学模块

电化学模块考虑储液罐和电堆中钒离子的影响因素，量化钒离子通过膜的转移，结合充放电氧化还原反应、交叉自放电反应和Fick定律建立质量平衡方程式，已知堆栈电压与单体个数和平衡电势有关，通过建立质量平衡方程式与电路模型相结合。各价钒离子浓度在储液罐和电堆中的动态微分方程式如式（8）～（9）所示。

在储液罐中

在电堆中

式（8）和（9）中：Vs是电堆内电解液总体积，Vt是正/负储液罐内电解液总体积，已知正负极体积保持一致；Csi和Cti（i=2,3,4,5）是电堆和储槽内的i价钒离子浓度；t代表时间；ki是i价钒离子的透膜扩散系数；F是法拉第常数；z为电子转移系数；d是离子膜厚度；S是离子膜面积；Qn为电解液流进电堆的流量；Id表示电流的充放电大小，符号±和∓，分别表示充电和表示放电。式（9）左边的项表示电堆内电解液浓度Csi的时间变化，右边的项中Qn(Cti-Csi)表示电解液在储液罐与电堆之间循环而引起i价钒离子浓度变化的影响因素，以及电堆内充放电氧化还原反应、交叉自放电反应引起的i价钒离子的浓度变化，负号表示减小，正号表示增加。

根据电堆中的各价钒浓度Csi，通过Nernst方程得到每个单体的开路电池电压Ucell，已知单体一致

在Nernst方程中，Ueq是温度为298 K时，VRB发生电化学反应正负极的标准电极电势，即1.259 V；F是法拉第常数；R是通用气体常数；z是每摩尔还原或氧化物质转移的当量数；T表征温度对电池运行的影响。

内部堆栈电压Us表征为受控电压源，且受控电压主要由串联的单体的数量Ncell和开路电压Ucell确定。因此堆栈电压为

全钒液流电池系统的荷电状态SOC表示VRB中实际容量与其额定容量的比值，它在0（完全放电状态）到1（完全充电状态）之间变化。可以通过测量正负极中电解液的钒离子价态及浓度来计算。由以下关系式定义[17]

在正极电解液中

在负极电解液中

2.3 流体力学模块

在全钒液流电池中，除了电堆中电化学反应，还需要考虑循环泵和电堆结构中电解液流量对电池的影响，主要包括电解液流经电堆和储液罐之间的管道产生的管道压力损耗和电解液在电堆内部流动而产生的电堆损耗，在等效电路中表征为可变电流损耗。

管道中的压力损耗可分为由于摩擦引起的沿程损耗ΔPfrication和与弯曲、阀门和其他配件相关的局部损耗ΔPpart，管道中的总压力损耗ΔPhydr见式（14）

沿程损耗应用在流体动力学中最广泛使用的Darcy-Weisbach方程

其中：fD是达西摩擦系数，L是管道的长度，D是管道的水利直径，ρ是流体的密度，Vs是管道电解液流动的平均速度。

其中fD可表示为

其中Re为雷诺系数

其中μ是流体的动力黏滞系数。

水利直径D定义为

其中，A为电解液的横截面积；L为电解液与管道接触的周长，即管道长度。

此外，管道中的局部损耗可表示为：

其中fL是局部损耗系数。在常见的VRB系统中，与由于管道中的摩擦引起的沿程损耗相比，管道中的局部部件引起的损耗可以忽略不计。管道中的体积流量与流速关系见式（20），可以代入Darcy-Weisbach方程。

电池堆栈由Ncell个平行的单体电池组成，全钒液流单体电池主要由离子交换膜，双极板，多孔电极（碳毡）等组成。电堆中的压力损耗包括流动框架和多孔电极的压力损耗，流动框架通常由支流管道和通道组成，假定电解液通过支流管道均匀地分布到每个单体电池中，电解液在电堆内的流动形式是层流，因此电堆内的压降与流量成正比，即

式中的比例系数R为电堆流阻。电堆的结构非常复杂，流阻很难用解析的方法描述。此前已有文章利用有限元分析的方法得到单电池的流阻，在此引用数据R˜。根据具体配置和流动框架设计，VRB系统的正侧或负侧的总压力损耗是如上所述的VRB系统的所有部件中的压力损耗的总和[18]。流体力学模型与泵损功率ΔPpump有关，可定义为

其中：ΔPpump是作为流速函数的总压降，α是取决于泵配置和操作条件的泵效率。建立与等效电路模型的联系，进而健全对全钒电池系统整体性能的研究。

2.4 混合建模

VRB混合模型分为三个模块：等效损耗电路模块、电化学模块、流体力学模块，见图3。

在电化学模块中，以充放电电流大小Id、VRB系统参数、电解液流量Qn以及各价态离子的初始浓度作为电化学模块的输入；通过电化学反应的动态微分方程式（8）和（9），得出各价钒离子浓度实时浓度，其中储液罐中钒离子浓度计算出SOC值，电堆中钒离子浓度通过Nernst方程（10）得到单体开路电压Ucell；已知各单体性质一致，再根据单体数量计算堆栈电压Us；Us作为等效电路中的受控电压源。在流体力学模块中，根据循环泵的流量（这里考虑与电解液流量一致）结合全钒液流电池液压回路的基本特性，计算出由循环泵引起的电堆压降ΔPhydr以及管道压降ΔPstack；然后得到的总压降ΔPpump可以根据流量和泵效率得到泵损功率Pp；而再考虑由全钒液流电池系统反馈的端电压得到泵损电流Ip；将Ip作为等效电路中的受控可变电流源。系统中的其他损耗等效为电阻，计算出等效电路中的各个参数值，结合受控电压源Us和受控可变电流源Ip，即可测量出全钒液流电池的等效工作端电压Ud。

3 全钒液流电池流量控制

3.1 最优流量选择

已知在恒流条件下，只有一个控制变量电解液流量Q，电堆功率和泵损功率受流量影响。在仿真模型中，分析流量Q对电池的特性影响。

在充电过程中，功率损耗由外部电源提供，则钒电池系统功率为电堆功率与损耗功率之和，最优流量值应使系统功率P最小[10]。

在放电过程中，功率损耗由电堆提供，则钒电池系统功率为电堆功率与损耗功率之差，最优流量应使电堆功率与总损失之差P最大[10]。

定义电池瞬时工作效率

其中：Pstack为电堆功率，Ploss为总功率损耗。

3.2 基于混合模型的流量特性分析仿真

在MATLAB/Simulink进行仿真实验，通过对不同流量值Q进行仿真，得到不同SOC下系统的瞬时工作效率η。针对不同的SOC值，在充电状态下,使瞬时工作效率η最大的流量值Q即为最优流量值；在放电状态下，使瞬时工作效率η最小的流量值Q即为最优流量值，仿真图见图4。

4 仿真结果分析

4.1 电池参数选择

本模拟中使用的GEC-VRB-5 kW/30 kW·h VRB电池，该电池由5 kW电堆和1.5 mol/L钒电解液（储液罐）组成，其中电堆由39个单电池组成，理想的膜应具有低钒离子渗透性，高质子传导性，良好酸溶液中的化学稳定性、良好的机械完整性以及低成本，本文选用GEC-IEM-107全氟离子交换膜来分离电堆中两种半电池溶液，相应的钒离子扩散系数选取温度在298 K时参数。此外，假设操作期间的平均电池电阻率为常数。表1列出了VRB的规格和本模拟中使用的参数。

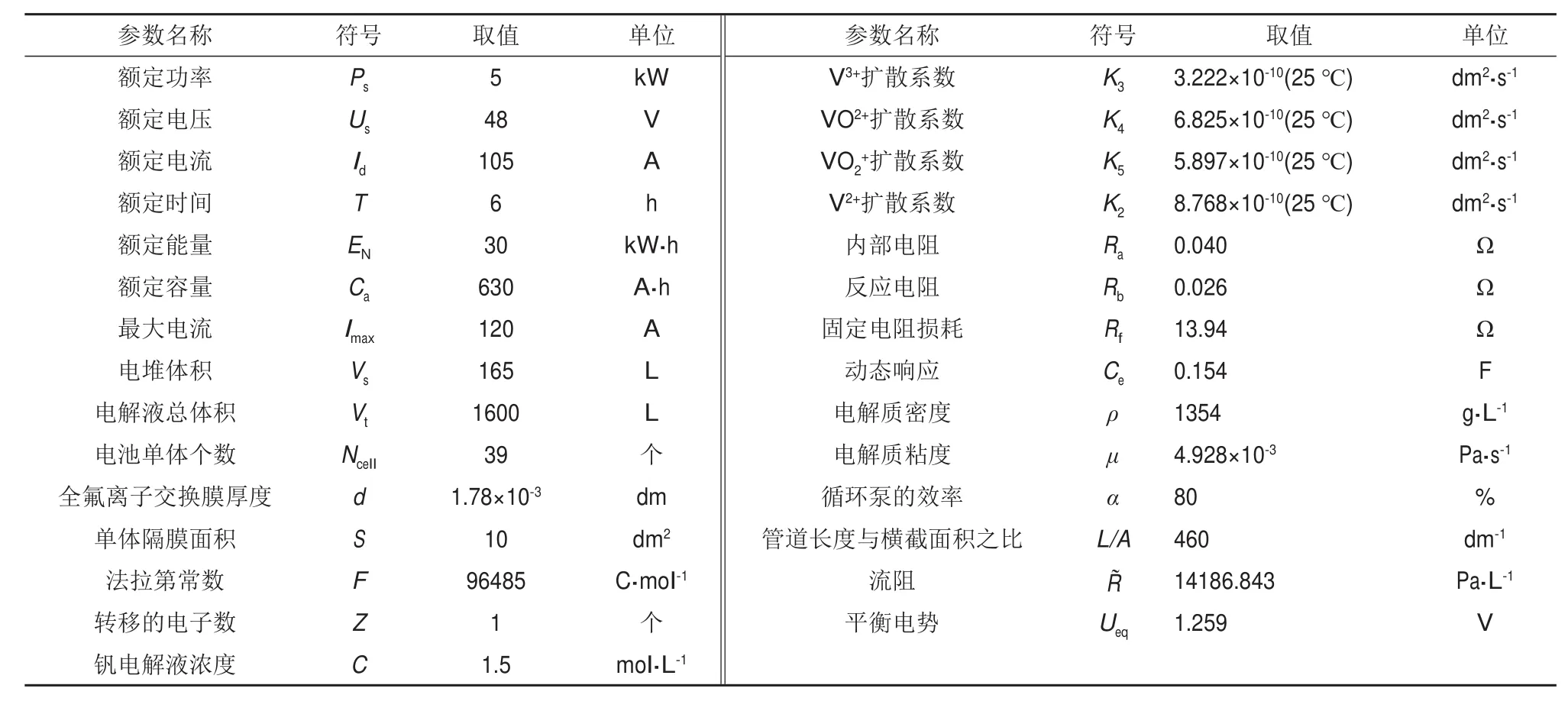
表1 5 kW/6 h VRB参数Table 1 5 kW/6 h VRBparameters

4.2 不同状态下VRB仿真结果分析

4.2.1 开路状态

模拟将VRB置于开路状态，在3.1中的电池系统参数基础上，设置初始条件，电堆和储液罐中的初始钒离子浓度均取值为：V2+和VO2+均为1.35 mol·L-1，V3+和VO2+均为0.15 mol·L-1。且自放电反应仅发生在电堆中，假设电堆开始时充满电解液，不开启循环泵，此时Qn为0，储液罐不提供电堆电解液，储液罐内离子浓度不发生变化。开路状态时，电堆中4种价态钒离子浓度随时间变化的仿真曲线如图5（a）所示，VRB的堆栈电压变化特性曲线如图5（b）所示。

从图5（a）可以看出，VRB在处于开路状态下，由于离子扩散作用的影响，在电堆中发生自放电反应，见公式(4)～(7)，导致电堆中各价钒离子的浓度随时间变化而变化。由图可知，在给定的电池参数和初始钒离子浓度的工作条件下，随着时间变化，电堆中正极的VO2+减少、VO2+增加，负极的V2+减少、V3+增加，直至V2+约在11.32 h最先耗尽，此时电堆中的钒离子中只存在V3+、VO2+、VO2+三种价态，此时发生的电化学反应只有公式(5)，V3+减小，VO2+增加，VO2+减小，VO2+的正负极浓度差降低，浓度变化越来越慢，直至负极的VO2+耗尽，约15.86 h，自放电反应结束，符合电堆电化学基本原理。图5（b）可以看出，堆栈电压随时间变化有两段呈指数趋势下降的特性曲线。电解液中钒离子的浓度和组成成分直接影响VRB的堆栈电压。在自放电反应进行到11.32 h时V2+耗尽，负极的V2+和V3+离子电对消失，堆栈电压存在一定程度的电压跌落。在15.86 h时VO2+耗尽使得正极的VO2+和VO2+离子对消失，堆栈电压再次极速下降直到一个稳定数值。

4.2.2 充放电状态

模拟VRB充电和放电状态，给定恒定105 A直流电流为激励对电池系统进行充放电，电堆和储液罐中的 V2+、V3+、VO2+、VO2+4种价态钒离子初始浓度分别取值：0.15、1.35、1.35和0.15 mol·L-1（初始SOC=0.1）。充放电过程中开启循环泵，令Qn=0.5，储液罐提供电堆电解液，储液罐内离子浓度随之变化，SOC值控制在0.1～0.9。

在VRB充放电运行中，电堆和储液罐中的各价钒离子浓度变化曲线如图6（a）所示，在图6（a）取时间段18000～28000 s，观察各同价态钒离子的浓度在电堆和储液罐的值，并将值扩大10倍，V3+和VO2+浓度曲线如图6（b）所示，V2+和VO2+浓度曲线如图6（c）所示。VRB的充放电电压和电堆堆栈充放电电压随荷电状态而变化的曲线如图6（d）。充放电时SOC曲线变化如图6（e）。

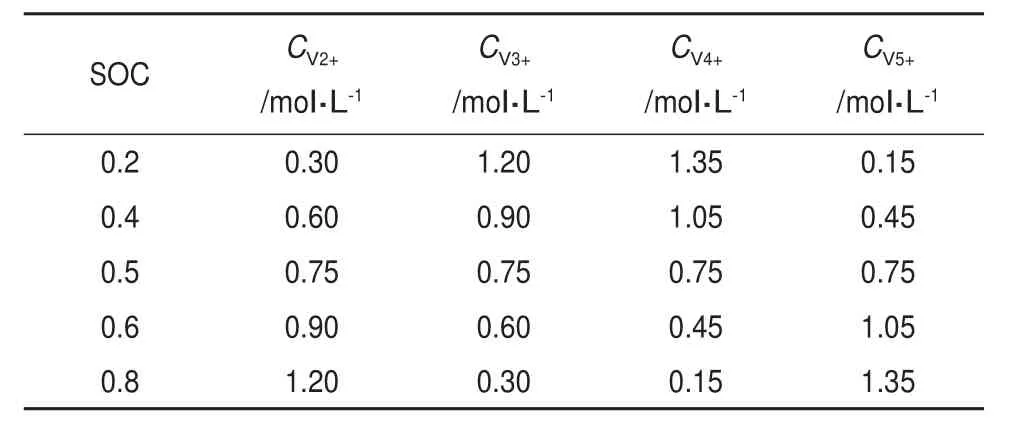
图6（a）显示，在充电过程中各价钒离子浓度变化，取图6（a）中的18000～28000 s时间段，从图6（b）可以看出，在充电过程中，Cs3Ct3且Cs4>Ct4。图6（c）可以看出，在充电过程中，Cs2>Ct2，Cs5>Ct5，但是在放电过程中Cs2

从图6（e）中可以看出，荷电状态保持在0.1～0.9之间，呈现线性变化趋势，电池不会出现过充和过放现象。

基于上述仿真分析，验证了电化学模型符合电池原理。

4.3 流量对电池性能影响

不同的SOC对应不同的初始钒离子浓度，在此假设钒离子的总浓度为1.5 mol·L-1，SOC取不同的值时对应的钒离子初始浓度，如表2所示。

表2 初始SOC对应的离子浓度Table 2 Ion concentration corresponding to initial SOC

通过对混合模型的MATLAB/Simulink进行仿真，图7为充电状态下，流速分别为0.18 L·min-1、0.3 L·min-1、0.48 L·min-1、0.6 L·min-1时的系统能量，纵坐标为η。

由图7可知，最优流速在0.3 L·min-1左右。分别对流速为0.306～0.33 L·min-1（间隔为0.003 L·min-1），进行仿真，仿真结果如图8所示。

分别对图8中SOC=0.2、0.3、0.4、0.5、0.6、0.7、0.8处进行放大，结果如图9所示。

表3为充电时最优流量与SOC的关系，由表3可知，随着充电的不断进行，荷电状态（SOC）不断增大，最优流速先减小后增大。

放电时最优流量为使瞬时工作效率η最小时的流量，分析方法与充电情况下类似。充放电过程中电池功率与流量的关系曲线见图10。由图10可知，充电状态下，当荷电状态（SOC）一定时，随着流速增大，P先减小后增大，存在极小值点；放电状态下，P先增大后减小，存在极大值点。

表3 充电时最优流量与SOC的关系Table 3 Relation between optimal flow and SOC

如图10（a）所示，充电状态下，随着流量增大，电池输入功率先减小后增大，这是因为在相同的荷电状态下，流量过小，电化学反应所需要的电解液量不能得到满足，需要更多的输入功率提供电化学的反应，流量过大，泵损也越大，输入功率也越大。在不同的荷电状态下，最优流量应使输入功率的比值越小。充电初期，SOC最小时，最优流量为最大值，是因为单位时间内需要可供反应的活性物质增大，流量需求有所下降并维持稳定；在充电中期，约在SOC为0.5时，流量值最小效率最高，但流量过小的话，不足以支持电堆内电化学反应，系统停止工作；在充电末期需要在合适范围内加大流量完成充电。如图10（b）所示，放电状态下，在不同的荷电状态下，最优流量应使输出功率越大，仿真运行的结果中可以看出，放电期间最优流量的趋势和充电期间相同。

流量Q越大，泵损电流Ip越大，泵损功率也越大；但Ip越大，流经电堆的堆栈电流Is越小，电堆中离子浓度变化率与流量Q和堆栈电流Is相关，进而影响着电堆功率。所以在充放电过程中需要根据SOC值调节泵速使得效率优化。在充放电工作过程中，对SOC分段取流量值，观察电池瞬时工作效率。

针对不同的SOC采用表3中的最优流速，实现变流控制，见图11。由图11可以看出，采用变流控制比恒流状态下系统效率有所提高。