巧用数形结合提升学生的数学素养
2020-04-02潘桢妍
潘桢妍

[摘要]数形结合是数学中的重要思想方法。数学教学中,教师要结合教材的特点和学生的认知水平,处理好数与形的结合;要以形助数,让数学概念、性质等更直观,同时通过数形结合提高学生的思维能力和审美能力,促进学生发现数学之关,不断提升学生的数学素养。
[关键词]数形结合;数学思想方法;数学素养
[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068(2020)08-0064-02
数形结合是数学学习中的重要思想方法。数形结合是一个双向过程,数学教学中教师要结合教材的特点和学生的认知水平,处理好数和形的关系。在小学数学教学中,笔者将数学结合思想融入课堂教学中,使学生在学习数与代数、空间与图形、统计与概率等知识时能融会贯通,把抽象的数学概念形象化、直观化,帮助学生理解算理,掌握算法,提升学生的数学素养。
一、以形助数,让数学概念、性质等更直观,提升学生的数学素养
数学概念、性质、意义的学习非常抽象、枯燥,数形结合可把抽象的概念转化为直观、形象的图形,使学生容易理解,从而产生学习兴趣。对此,在教学中教师应以形助数,让数学概念、性质、意义更加直观。
例如,在执教“乘法的初步认识”时,利用游乐场主题图来引入乘法。教师先利用PPT出示主题图,让学生选择喜欢的项目,并数一数有多少人参加此项目。学生会用连加的方法来算出“飞轮转移”的人数:2+2+2+2+2+2=12;划船的人数:3+3+3+3=12。接着教师出示停满船只的湖面,提问:“如果有20条船、30条船、40条船,怎么计算人数呢?”然后进行归纳总结,引出用乘法算式表示船的条数乘一条船的人数或一条船的人数乘以船的条数。这样通过以“形”助数,使学生既直观理解了乘法的意义,又明白了乘法是同数相加的简便运算,使得建立乘法概念水到渠成。而在“我来挑战”这一环节中,教师又设计了这样的题目:把下面的加法算式改写成乘法算式。
一千个a、一万个a、一亿个a相加,怎样用乘法算式表示呢?
通过这类题目的设计,使学生经历了由具体到抽象、由简单到复杂的思维过程。利用数形结合强化乘法算式的学习,有助于学生对数学模型的建立。
数形结合对培养学生的思维能力起着重要的作用。教师在教学中巧用数形结合,可大大提升学生的思维能力和数学素养。
二、以形助数,帮助学生理解算理,提升学生的数学素养
小学数学练习中有相当一部分内容是计算题,计算题有着独有的算理,所以计算教学的一个重要内容就是帮助学生理解算理,即计算方法的道理,让学生在计算过程中不仅要“知其然”,更要“知其所以然”。以形助数就是一个帮助学生正确理解算理的好方法。
通过图形演示,学生直观地理解了“通分”的必要性和异分母分数加减的算理,这是空洞的说理和训练所达不到的效果。这种数学结合的方法在小学数学计算教学中运用越来越广泛。以形助数是进行数学推理的“向导”,也是数学学习的有效思维策略。当解题思路受阻时,数形结合可作为寻求解题思路的突破口。因此,数形结合思想在解决数学推理问题上有着积极的意义。
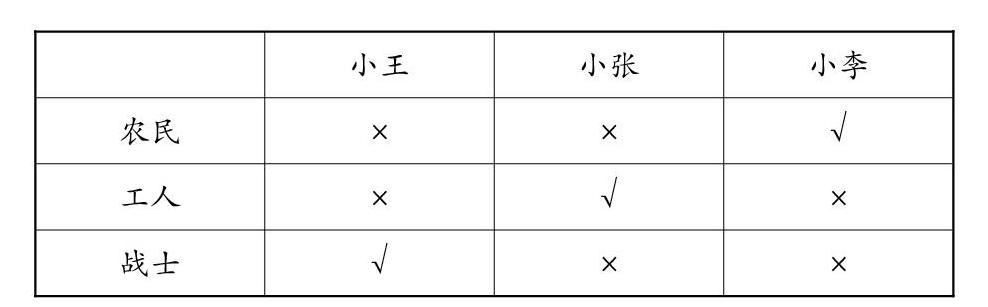
例如,笔者8岁的女儿做作業时,遇到这样一道推理题:小王、小张和小李在一起,一位是工人,一位是农民,一位是战士。现在知道:小李比战士年龄大,小王和农民不同岁,农民比小张年龄小。那么,谁是工人?谁是农民?谁是战士?8岁的小孩,要解决这类问题还是比较困难的。于是笔者建议她先画一张表格(如表1),再根据题中所给的信息进行判断。
表格法是解决推理题的常用方法,它能帮助我们直观地进行判断,很快得出正确结论。可见,巧妙运用数形结合,可有效促进学生数学素养的提升。
三、数形结合,提升学生的思维能力
数形结合是提升学生思维能力的有效方法。在小学数学的解题教学中,教师应有效利用数形结合,不断提升学生的思维能力。
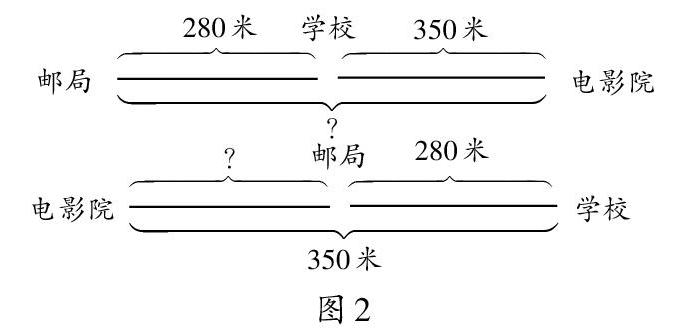
例如,在教学解决简单行程问题时,教师应引导学生读题,并画线段图,通过数形结合来理解题意,厘清解题的思路,把握数量关系。如三年级上册练习三第12题“本市的邮局、电影院和学校都位于创业大路,其中邮局距学校280米,电影院距学校350米,问邮局距电影院多少米?”,笔者先让学生自己思考解决。起初,大部分学生只考虑到邮局和电影院分别在学校的两旁,所以列出算式:280+350=630(米)。笔者适时提问点拨:你们能不能用线段图把电影院、邮局、学校的距离表示出来?这样引导,学生就能轻而易举地画出两种情况(如图2)。
又如,学生学完三年级上册“长方形和正方形的周长”后,对于例题“用16张边长是1分米的正方形纸拼长方形和正方形。怎样拼?周长最大是多少?最小是多少?”学生一开始看不懂。于是笔者提示:可以按照题目说的动手拼拼看,先想有多少种拼法,再想拼好后长方形和正方形的长和宽各是多少。在笔者的启发下,学生很快拼出了如下三种方法。
第一种:(16+1)x2=34(厘米)。
像这样,巧妙地把数形结合思想渗透在学生获取知识和解决问题的过程中,充分利用直观图形,把抽象内容视觉化、具体化,引导学生通过观察、分析、概括、实践,理解解题方法所蕴含的数学思想,使得学生的数学素养得到了质的飞跃。
四、数形结合,提高学生的审美能力
数学是一门涉及美学的课程,数学上的对称美、和谐美、奇异美等形式体现在图形上更为直观、形象,也更动人心弦。利用数形结合,可让学生体验到数学的美,培养学生的审美能力。
例如,在教学三年级上册“分数的初步认识”后,教师可利用数形结合,出示分数砌成的“分数墙”(如图3)。
(1)在“分数墙”里能找出哪些分数?把它们从小到大排列。
(3)哪几个分数相加的和等于17
有了“分数墙”,在给足学生观察、体验的空间和时间后,就能从“分数墙”中引领学生追求数学学科的本质,促进学生数学思想的形成、发展,提升学生的数学素养。
例如,六年级上册“比”这个单元让学生感受到了黄金比的比例之美。把一条线段分成两部分,较短部分和较长部分之比等于较长部分与整体长度之比,这个比我们称之为黄金比(约为0.618:1)。生活中,许多物品的设计(如图4)都含有黄金比这一因素。这些按照黄金比制作的图形常常给人一种优美的视觉享受。
综上所述,作为小学数学教师,在教学中要有数学发展观,要从课堂教学设计入手,有目的、有计划地应用数形结合,使学生在数学学习、解题中掌握数学知识和解题方法,从而培养学生的学习能动性,提升学生的数学素养。
(责编:黄春香)
