基于数据驱动的非球形散体颗粒休止角智能建模方法

胡 洲，刘小燕，武伟宁

基于数据驱动的非球形散体颗粒休止角智能建模方法

胡 洲，刘小燕，武伟宁

(湖南大学 电气与信息工程学院，长沙 410082)

针对离散单元法(DEM)仿真非球形散体颗粒休止角计算量大、耗时长的问题，本文基于DEM历史仿真数据，采用数据驱动的智能建模方法—BP、RBF神经网络建立非球形散体颗粒的休止角模型，并与传统克里金回归方法进行比较。结果表明，智能模型的运算速度相比DEM计算速度有很大提升；智能模型相比传统克里金回归模型具有更佳的预测性能，其中BP神经网络模型综合性能最优。最后，采用BP神经网络模型分析颗粒形状及摩擦因数对休止角的影响，发现休止角随颗粒形状变量、摩擦因数的增加都呈现增大的趋势，与现有研究结果一致，进一步证明了智能模型进行休止角预测的可靠性。

非球形散体颗粒；休止角；智能模型；离散单元法

散体颗粒广泛存在于自然界中，如金属粉末、矿物砂石等，在工业生产中扮演着重要的角色[1, 2]。休止角是散体颗粒堆自由表面与水平面的夹角[3]，能将散体颗粒的微观行为与其宏观行为相关联，是表征散体颗粒流动能力的重要物性参数[4]，近年来被广泛研究及应用[5−7]。目前用于获取散体颗粒休止角的物理实验测量方法有：倾斜盒法[8]、转筒法[9]、空心圆柱法[10]等。然而，采用物理实验方法很难获取颗粒微观行为变化对休止角的影响。

离散单元法(Discrete element method, DEM)是一种专门用于求解和分析散体颗粒运动规律与力学特征的数值模拟方法。DEM在每个时步都能获取颗粒的受力情况[11−12]、运动轨迹[13]、颗粒速度[14−15]等物理实验测量方法很难检测的微观信息。但DEM的缺点在于仿真计算量大、获取结果耗时长。虽然采用先进的GPU-DEM仿真技术[16]仿真一个包含960万个球形颗粒的系统已经可以达到准实时状态(计算时间与物理时间之比可达9.37:1)，但是该平台的搭建相当复杂且价格昂贵(包含270个GPU卡，NVIDIA C2050)。针对DEM运算速度的瓶颈问题，目前解决的方法主要有两种。第一种方法，使用较大的颗粒进行仿真[17]，可以减少系统中的颗粒数量，进而缩短仿真时间。而为了获取新的输入参数对应的结果，仍需进行长时间的仿真计算，且在使用该方法前，需调节颗粒密度以保证颗粒之间相似的动量交换[18]。第二种方法，基于DEM仿真历史数据，采用数据驱动的方法，建立输入变量与输出结果间的关系模型，以替代原DEM模型。虽然该方法仍然需要前期的DEM仿真数据，但在建立好关系模型后，可以迅速预测新样本的结果[19]，避免输入参数发生变化时再次进行长时间的DEM仿真。目前，基于DEM历史仿真数据对休止角建模的研究较少。RACKL等[20]基于DEM历史仿真数据，采用传统克里金(Kriging)回归方法建立了休止角与颗粒密度、弹性模量、颗粒摩擦因数之间的元模型(Meta- model)，然而克里金回归模型预测的休止角与DEM仿真的休止角之间的相关系数不到0.72，精度低。并且，克里金回归算法预测时需要考虑所有样本点对预测点的影响，因此计算速度较慢。为进一步提高预测速度及精度，近三年来有学者开始尝试利用智能算法对颗粒休止角进行建模。BENVENUTI等[21]基于81组休止角DEM历史仿真数据，使用BP神经网络建立了颗粒恢复系数、颗粒摩擦因数、颗粒密度等与休止角的智能模型，但仿真中使用的都是球形颗粒，作为影响休止角的重要因素—颗粒形状在建模过程中并未考虑。事实上，自然界和工业中广泛存在的颗粒基本为非球形，因此，上述的休止角预测智能模型存在较大的局限性。

针对上述问题，本文进行了78组非球形颗粒休止角的DEM仿真；基于DEM历史仿真数据，使用BP神经网络、RBF神经网络智能建模方法，建立非球形散体颗粒休止角的智能模型(示意图见图1)；对休止角智能模型的运算速度及预测性能进行测试；并讨论隐含层节点数对休止角智能模型的影响；最后，分析颗粒形状变量与颗粒摩擦因数对休止角的影响。

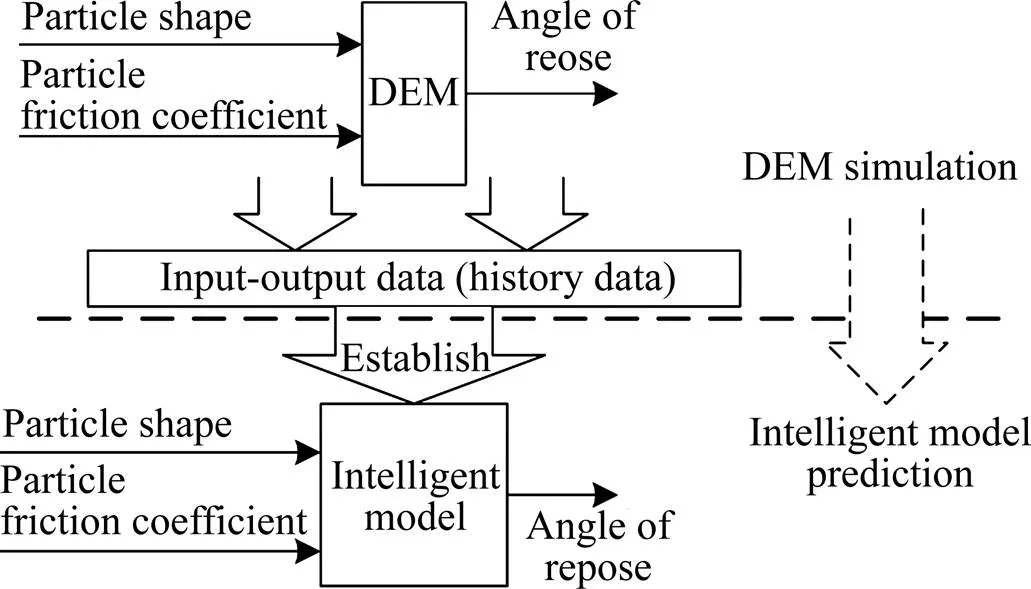
图1 休止角智能建模示意图

1 非球形颗粒休止角的DEM仿真

影响休止角的因素很多，如颗粒形状、摩擦因数、恢复系数等，KHANAL等[22]使用DEM构造不同长宽比的簇颗粒(Clumps)研究了颗粒形状对休止角的影响，发现颗粒形状对休止角有显著影响；HU等[23]使用DEM研究了泊松比、剪切模量、恢复系数及颗粒摩擦因数对休止角的影响，发现颗粒摩擦因数对其影响最大；COETZEE[24]使用不同子球个数的簇颗粒研究了不同颗粒摩擦因数下颗粒形状对休止角的影响，发现颗粒形状和颗粒摩擦因数对休止角影响显著。因此，本文对休止角的DEM仿真主要考虑颗粒形状和颗粒摩擦因数的影响。

1.1 非球形颗粒的模拟

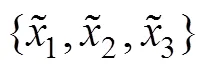
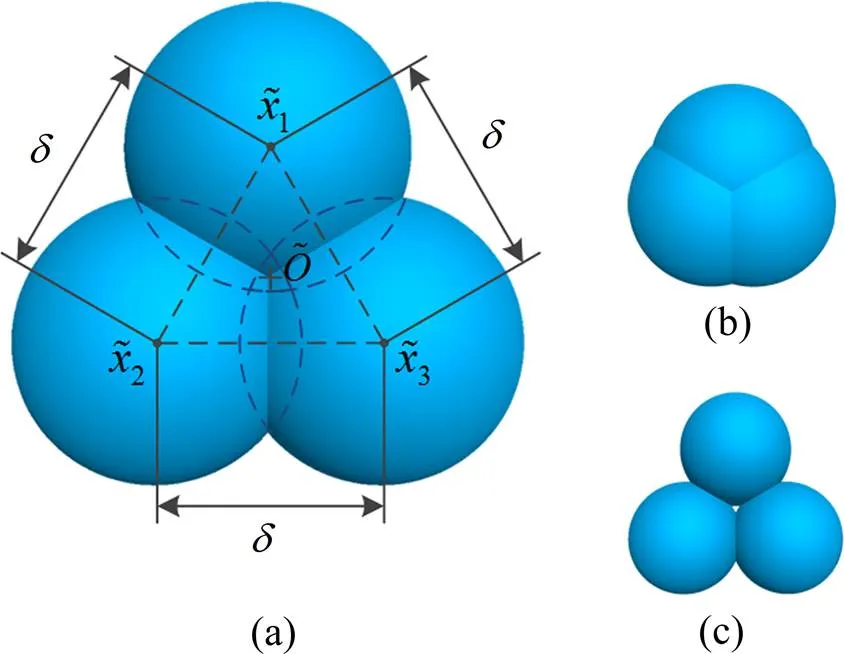
图2 非球形颗粒示意图

1.2 DEM仿真步骤

本文采用最易实现的空心圆柱法对簇颗粒的休止角进行仿真，使用的接触模型为非线性Hertz-Mindlin模型[27]，其余仿真参数见表1所示。具体仿真步骤如下：

表1 DEM仿真参数

图3 非球形颗粒休止角DEM仿真过程示意图

1) 在直径为91 mm、高为136.5 mm的垂直圆柱筒内(见图3(a))，生成7000个球形颗粒；

2) 用等体积的簇颗粒以随机方向对球形颗粒进行替换，在重力作用下，仿真1 s，使颗粒沉降，如图3(b)所示；

3) 以16 mm/s的速度提升圆柱筒，使颗粒从形成的缝隙流出(图3(c)和(d)所示分别为上提1 s、3 s时刻的状态图)，仿真持续6 s，以形成稳定的颗粒堆，如图3(e)所示；

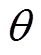
按以上步骤，在CPU为Intel® Xeon® Processor E5–2640 v2、内存为32 GB的计算机上，使用PFC3D5.0进行一组非球形颗粒休止角的DEM仿真，大约需要花费153 min。

1.3 DEM仿真结果

2 基于神经网络的休止角智能建模方法

人工神经网络(Artificial neural network, ANN)已被证明能够解决许多经典数学和传统过程难以求解的复杂工程问题[28]，被广泛用于医学、工程、数学建模等研究应用中[29]。人工神经网络有多种结构形式，其中BP神经网络和RBF神经网络是使用最多的两种神经网络[29]。本文采用三层网络结构对非球形颗粒休止角进行智能建模，如图4所示。

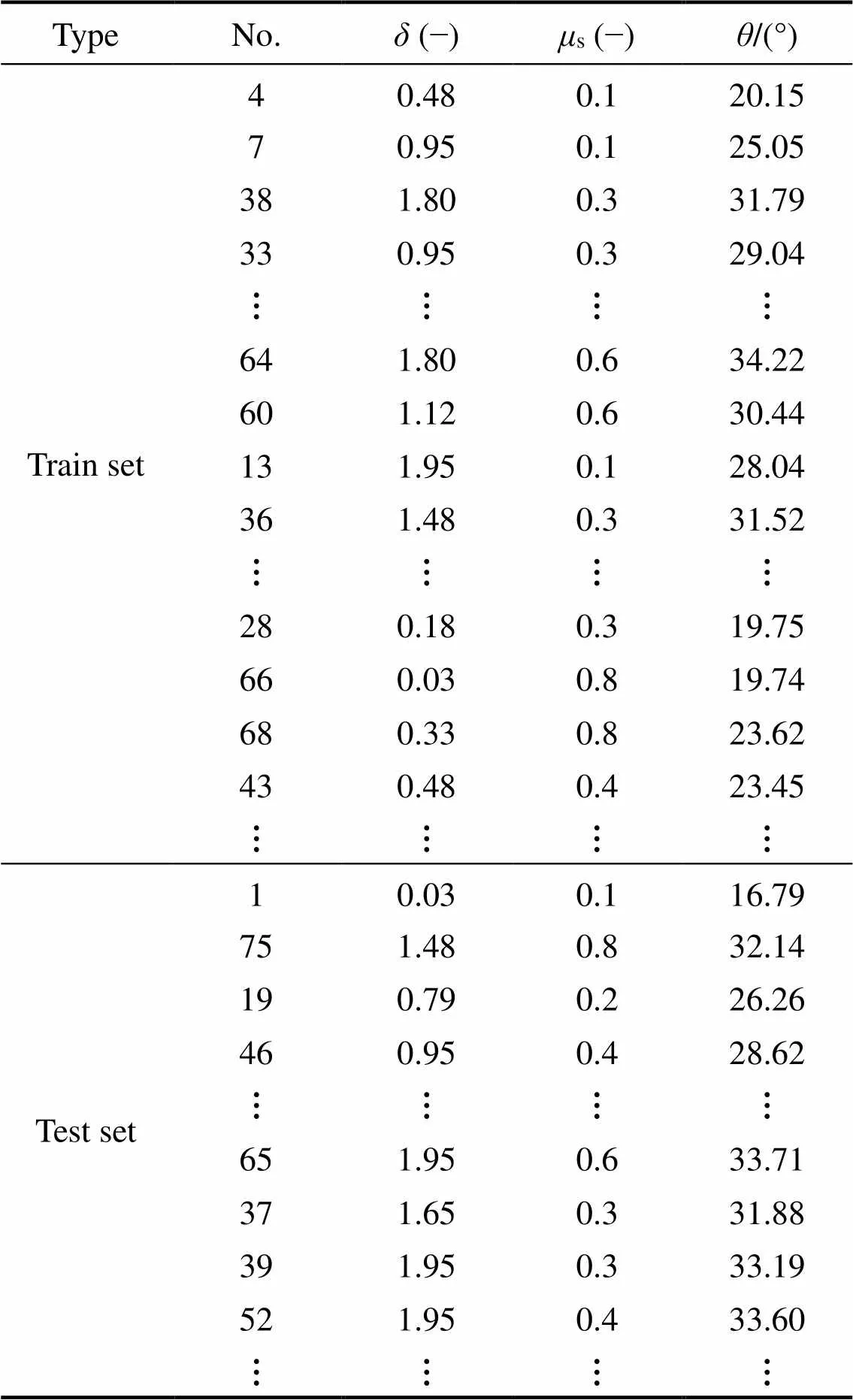
表2 非球形颗粒休止角DEM仿真结果示例

2.1 BP神经网络

采用误差反向传播算法(Error back propagation, BP)的神经网络是目前使用最为广泛的人工神经网络，其中单隐含层网络的应用又最为普遍[30](见图4)，每层的神经元节点通过权值与下一层的节点相连接。输入信号通过非线性函数转换成输出结果，最后，网络输出如下：

图4 本文使用的神经网络结构

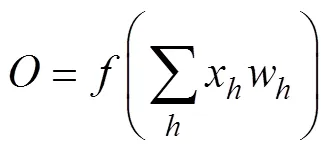
当网络输出与目标值不等时，存在输出误差，定义如下：

为了减小误差，BP神经网络使用梯度下降反向传播算法[29]对网络权值进行调整。该算法要求每个训练样本都包含输入和对应的输出值(目标值)。本文使用min-max方法对训练样本进行标准化处理。训练时，以随机数给网络权值赋初值，然后对权值进行优化调整，直到误差小于设定值0.001或达到设定的最大训练次数200000。

2.2 RBF神经网络

式中：、C分别为隐含层节点的输入和函数中心。

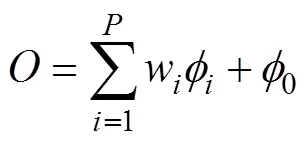
2.3 智能模型预测性能评价指标

为了测试比较休止角智能模型的预测性能，本文使用均方误差(Mean squared error, MSE)、决定系数(2)、Theil不等式系数(Theil’s inequality coefficient, TIC)[34]对休止角模型的预测性能进行评价，其具体计算公式分别如下：

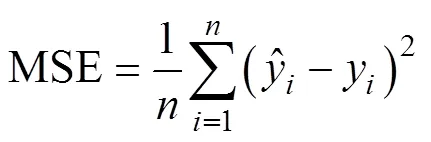
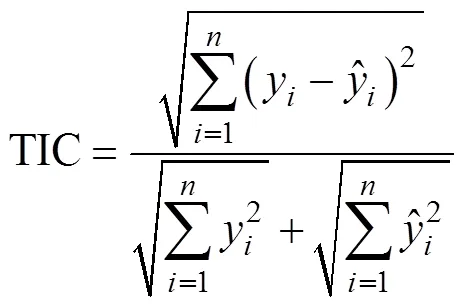
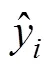
3 结果与分析

3.1 休止角智能模型的运算速度

在1.2节中提到，使用DEM仿真获取1组(7000个)非球形颗粒的休止角就需要花费大约153 min，而使用智能模型对32组休止角数据进行预测的时间均未超过1 ms(如表3所示)，即使用智能模型进行休止角预测的时间不到DEM仿真时间的1×10−7。对比智能模型的计算时间可以发现，RBF神经网络模型为用时最短的智能模型，其计算时间不到BP神经网络模型的一半，这是因为RBF神经网络的输入层只用于传输输入信号，且其输出层节点只进行线性加权求和运算。不过，相比计算量巨大的DEM仿真，休止角的BP、RBF神经网络模型的运算速度都处于同一数量级水平，远快于DEM仿真。

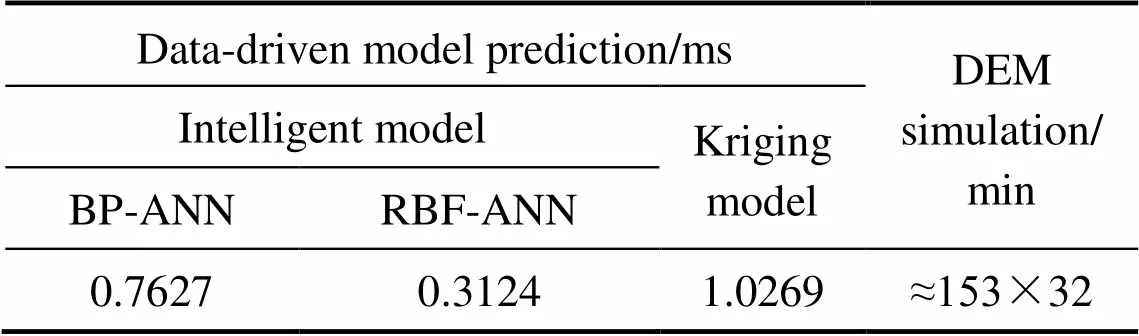
表3 休止角数据驱动模型预测时间与DEM仿真时间比较

3.2 休止角智能模型的预测性能

为了对建立好的智能模型的预测性能进行评价比较，采用BP、RBF神经网络模型对32组测试数据进行预测，并将其结果与文献[20]中使用的传统克里金(Kriging)回归模型的预测结果进行比较，如表4所示。

表4 基于数据驱动的休止角模型的预测性能指标

由表4可知，基于神经网络的休止角智能模型各预测指标的表现均优于传统克里金回归模型，且智能模型的运算速度更快(见表3)。进一步比较可以发现，BP神经网络模型的MSE为0.3530，TIC低至0.0108，2高达0.9875，为预测性能最优的的智能模型。这是由于RBF神经网络和Kriging都为局部逼近方法，而BP神经网络是一种全局逼近法，针对波动较大的休止角数据(休止角的测量误差很难小于±1°[17])，达到全局最优的BP神经网络在进行预测时能得到更好的效果。

为更直观地比较各模型的性能，绘制如图5所示的预测残差图。由图5可知，BP神经网络、RBF神经网络、Kriging模型预测的休止角误差区间分别为(−0.9771°~1.3154°)、(−1.6674°~1.1793°)、(−0.9160°~ 1.5159°)，BP神经网络模型的误差波动范围最小。

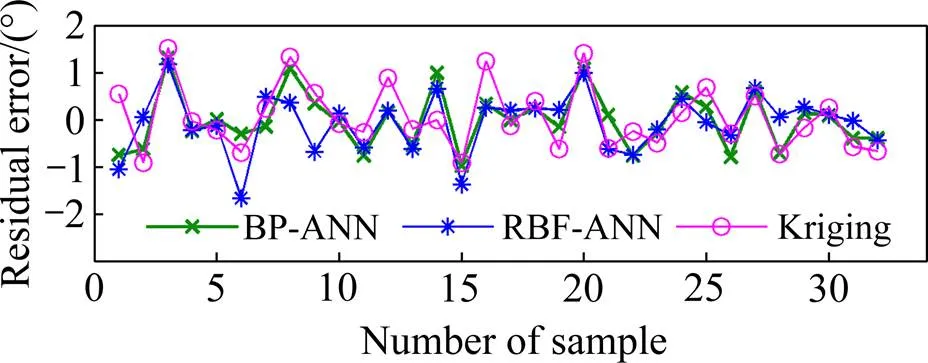
图5 智能模型预测的休止角与DEM仿真的休止角之差

3.3 隐含层节点数对休止角智能模型的影响

在本文使用的神经网络结构中(见图4)，输入层、输出层节点数分别由样本输入、输出变量个数确定，因此只需分析隐含层节点数对智能模型性能的影响。分别使用BP、RBF神经网络创建7个休止角智能模型，其隐含层节点数如表5所示。

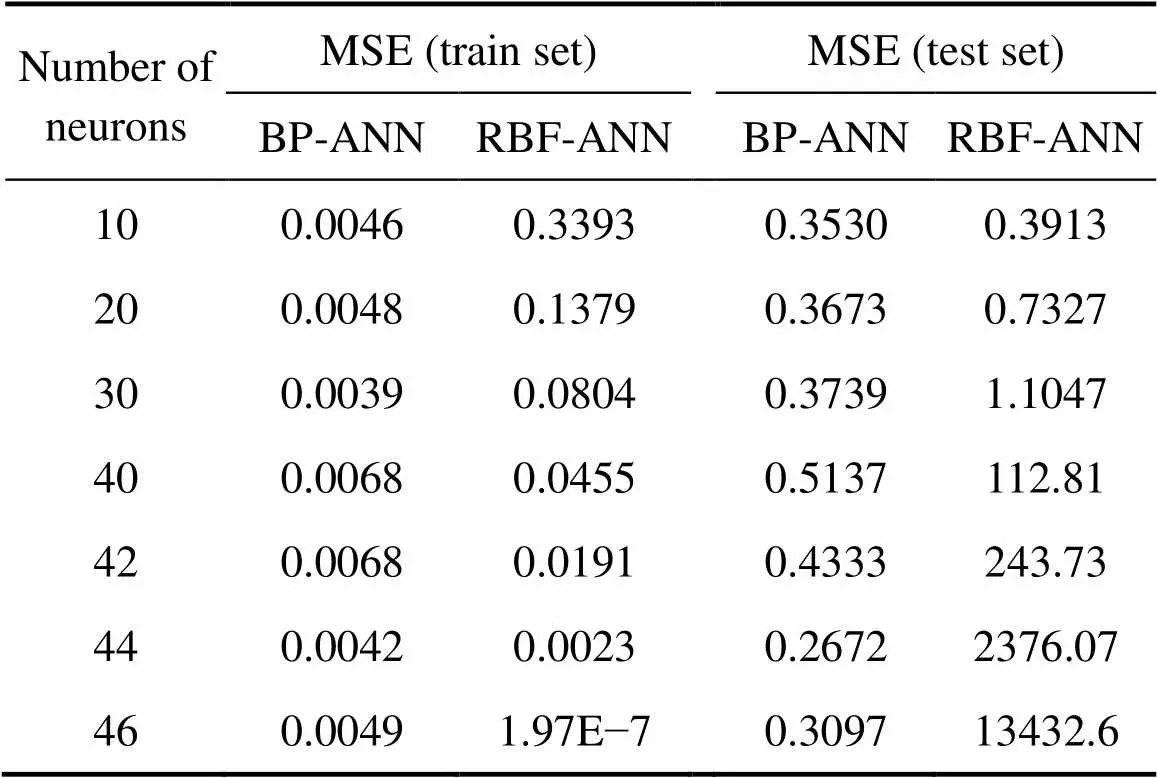
表5 不同隐含层节点数对休止角智能模型性能的影响

对于RBF神经网络增加隐含层节点数能够显著减小其休止角智能模型针对训练集的MSE，当隐含层节点数接近训练样本数时，RBF神经网络模型误差几乎为零，此时针对测试集的MSE显著增大，这是由于模型出现了过拟合，导致泛化能力变差。而对于BP神经网络，在训练时网络对目标的逼近能力和测试时网络的性能表现，隐含层节点数的变化对其影响都不大。因此，BP神经网络模型较RBF神经网络模型具有更好的稳定性。

3.4 颗粒形状及摩擦因数对休止角的影响

最后，本文采用综合性能最优的BP神经网络模型分析及s对的影响，如图6所示。、s的取值范围分别为0.1~1.9、0.1~0.8，间隔都为0.01，共包含12851个数据点。采用智能模型对如此大的数据量进行预测，仅需0.5067 s，与DEM仿真相比具有很大优势。分析图6可以发现：

1)随、s的增加呈现出增大的趋势。由于摩擦因数s越大颗粒越难产生滑动，因此，当形状变量不变时，如=1(红色实线)，休止角随s的增加从25°升高至30°；类似地，当s=0.4时(蓝色实线)，也可以观察到随的增加而增大的趋势(从小于19°到大于33°)，这是由于颗粒形状变量越大(即颗粒越不规则)，使得颗粒越难产生滚动，因此对应的休止角也将增大。这类趋势分别与文献[35]与文献[24]中观察到的趋势是一致的。

2)的最大值及最小值是、s联合作用的结果。的最大值34.1°和最小值18.5°分别出现在图6中右上角(红色区域，即＞1.5且s＞0.6的区域)和左下角(蓝色区域，即＜0.4且s＜0.3的区域)，结合第1)点的分析可知，这是颗粒形状变量和摩擦因数共同作用的结果。

3) 图6中左上(右下)角的对s()的变化并不敏感，这是因为该区域颗粒的运动方式主要为滚动(滑动)。在文中第1.1节已说明，越小簇颗粒越接近球形颗粒，则颗粒越容易发生滚动。当摩擦因数较大(s＞0.4)，而颗粒形状变量较小时(＜1.0)，即图6中左上角区域，对应颗粒的运动方式主要为滚动，因此，对s的变化不敏感，而对的变化很敏感，如蓝色虚线所示，随的减小出现明显降低。相反，当颗粒形状变量＞1.3而摩擦因数s＜0.4时(图6中右下角区域)，该区域对应颗粒的运动方式以滑动为主，因此，对的变化不敏感，而对s的变化很敏感，如红色虚线所示，随s的减小出现明显降低。该结论与文献[36]结论相吻合，也进一步表明智能模型的预测结果是可信的。

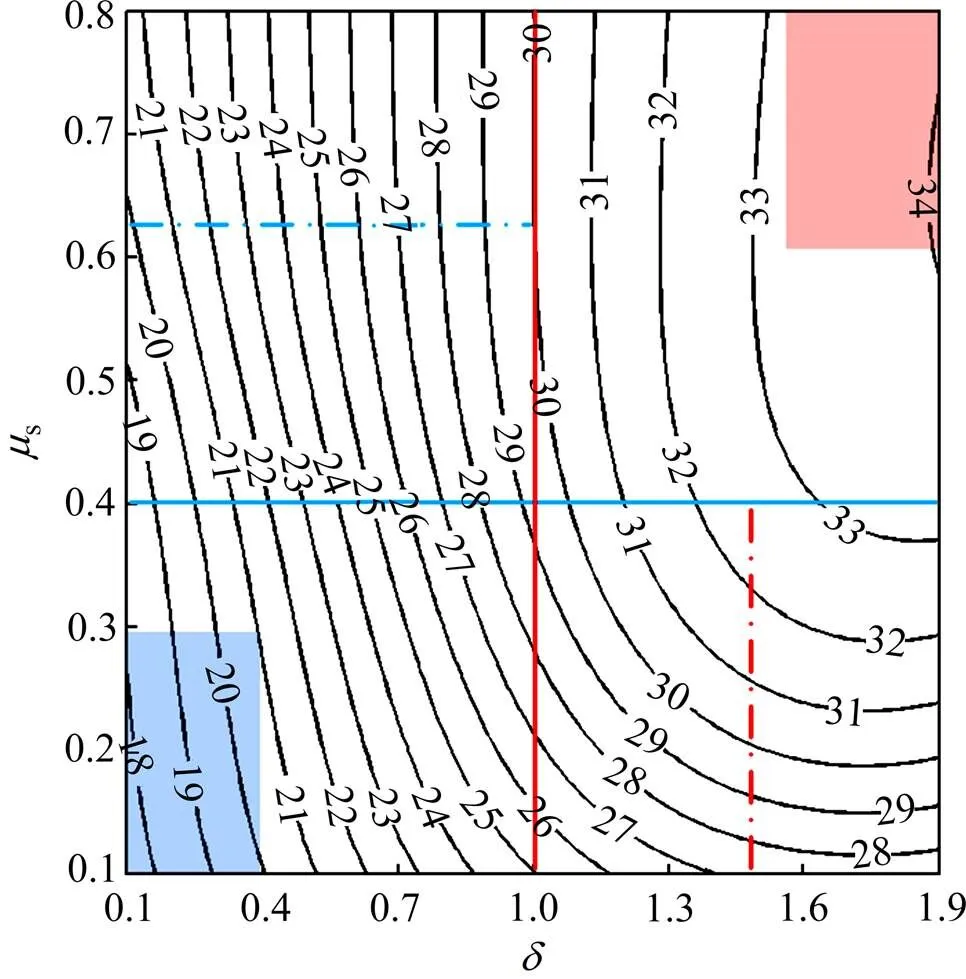
图6 休止角θ随形状变量δ和摩擦因数μs变化的等值线图

4 结论

1) 相比休止角的DEM仿真，智能模型的运算速度很快，因此可使用智能模型替换DEM仿真进行后期休止角的预测，避免再次运行长时间的DEM仿真。

2) 休止角的智能模型相比传统克里金回归模型有更快的运算速度和更优的预测性能。其中，BP神经网络模型的综合性能最优。

3) 采用BP神经网络模型分析休止角受颗粒形状和摩擦因数影响，所得结论与现有研究结论相一致，进一步表明该智能模型预测结果是可靠的。

[1] ZHU H P, ZHOU Z Y, YANG R Y, YU A B. Discrete particle simulation of particulate systems: A review of major applications and findings[J]. Chemical Engineering Science, 2008, 63(23): 5728−5770.

[2] 陈 辉, 刘义伦, 赵先琼, 肖友刚, 刘颖. 一元散体颗粒物料在回转窑截面上的运动与混合[J]. 中国有色金属学报, 2015, 25(5): 2575−2581. CHEN Hui, LIU Yi-lun, ZHAO Xian-qiong, XIAO You-gang, LIU Yin. Motion and mixing of mono-disperse granular material incross section of rotary kiln[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(5): 2575−2581.

[3] ILELEJI K E, ZHOU B. The angle of repose of bulk corn stover particles[J]. Powder Technology, 2008, 187(2): 110−118.

[4] GUO Zhi-guo, CHEN Xue-li, LIU Hai-feng, GUO Qiang, GUO Xiao-lei, LU Hai-feng. Theoretical and experimental investigation on angle of repose of biomass–coal blends[J]. Fuel, 2014, 116: 131−139.

[5] BEAKAWI AL-HASHEMI HM, BAGHABRA AL- AMOUDIOS. A review on the angle of repose of granular materials[J]. Powder Technology, 2018, 330: 397−417.

[6] LI Cheng-zhi, HONEYANDS T, O'DEA D, MORENO- ATANASIO R. The angle of repose and size segregation of iron ore granules: DEM analysis and experimental investigation[J]. Powder Technology, 2017, 320: 257−272.

[7] 张立栋, 李连好, 王 擎, 秦 宏, 李少华. 椭圆型混合器内二元颗粒径向混合[J]. 中国有色金属学报, 2017, 27(4): 825−832. ZHANG Li-dong, LI Lian-hao, WANG Qing, QIN Hong, LI Shao-hua. Transverse mixing of binary granular in elliptical mixer[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(4): 825−832.

[8] PITANGA H N, GOURCB J P, VILAR O M. Interface shear strength of geosynthetics: Evaluation and analysis of inclined plane tests[J]. Geotextiles and Geomembranes, 2009, 27: 435−446.

[9] DURY C M, RISTOW G H, MOSS J L, NAKAGAWA M. Boundary effects on the angle of repose in rotating cylinders[J]. Physical Review E, 1998, 57(4): 4491−4497.

[10] LIU Zhi-chao. Measuring the angle of repose of granular systems using hollow cylinders[D]. Pittsburgh: University of Pittsburgh, 2011.

[11] ZHOU W, LIU J, MA G, YUAN W, CHANG X. Macroscopic and microscopic behaviors of granular materials under proportional strain path: A DEM study[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(18): 2450−2467.

[12] 陈 辉, 赵先琼, 刘义伦. 变重力场中散体颗粒堆的安息角及接触力分布[J]. 北京航空航天大学学报, 2015, 41(6): 1141−1146. CHEN Hui, ZHAO Xian-qiong, LIU Yi-lun. Angle of repose and contact-forcedistribution in granular pile under veariable g[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1141−1146.

[13] XU Yong, XU Chun-hui, ZHOU Zhe, DU Jing, HU Da-ping. 2D DEM simulation of particle mixing in rotating drum: A parametric study[J]. Particuology, 2010, 8(2): 141−149.

[14] ALIZADEH E, BERTRAND F, CHAOUKI J. Comparison of DEM results and lagrangian experimental data for the flow and mixing of granules in a rotating drum[J]. AiChE Journal, 2014, 60(1): 60−75.

[15] ZHOU Y C, YU A B, STEWART R L, BRIDGWATER J. Microdynamic analysis of the particle flow in a cylindrical bladed mixer[J]. Chemical Engineering Science, 2004, 59(6): 1343−1364.

[16] XU Ji, QI Hua-biao, FANG Xiao-jian, LU Li-qiang, GE Wei, WANG Xiao-wei, XU Ming, CHEN Fei-guo, HE Xian-feng, LI Jing-hai. Quasi-real-time simulation of rotating drum using discrete element method with parallel GPU computing[J]. Particuology, 2011, 9(4): 446−450.

[17] ROESSLER T, KATTERFELD A. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles[J]. Powder Technology, 2018, 330: 58−66.

[18] HASSANPOUR A, TAN H, BAYLY A, GOPALKRISHNAN Prasad, NG Boonho, GHADIRI Mojtaba. Analysis of particle motion in a paddle mixer using discrete element method (DEM)[J]. Powder Technology, 2011, 206(1/2): 189−194.

[19] BARRASSO D, TAMRAKAR A, RAMACHANDRAN R. A reduced order PBM-ANN model of a multi-scale PBM-DEM description of a wet granulation process[J]. Chemical Engineering Science, 2014, 119: 319−329.

[20] RACKL M, HANLEY K J. A methodical calibration procedure for discrete element models[J]. Powder Technology, 2017, 307: 73−83.

[21] BENVENUTI L, KLOSS C, PIRKER S. Identification of DEM simulation parameters by artificial neural networks and bulk experiments[J]. Powder Technology, 2016, 291: 456−465.

[22] KHANAL M, ELMOUTTIE M, ADHIKARY D. Effects of particle shapes to achieve angle of repose and force displacement behaviour on granular assembly[J]. Advanced Powder Technology, 2017, 28(8): 1972−1976.

[23] HU Zhou, LIU Xiao-yan, WU Wei-ning. Study of the critical angles of granular material in rotary drums aimed for fast DEM model calibration[J]. Powder Technology, 2018, 340: 563−569.

[24] COETZEE C J. Calibration of the discrete element method and the effect of particle shape[J]. Powder Technology, 2016, 297: 50−70.

[25] FAVIER J F, ABBASPOUR-FARD M H, KREMMER M, RAJI A O. Shape representation of axi-symmetrical, non-spherical particles in discrete element simulation using multi-element model particles[J]. Engineering Computations, 1999, 16(4): 467−480.

[26] COETZEE C J. Review: Calibration of the discrete element method[J]. Powder Technology, 2017, 310: 104−142.

[27] ITASCA. PFC version 5.0 documentation[H]. Itasca Consulting Group Inc., 2017.

[28] MOHAMED M T. Performance of fuzzy logic and artificial neural network in prediction of ground and air vibrations[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(5): 845−851.

[29] YILMAZ I, KAYNAR O. Multiple regression, ANN (RBF, MLP) and ANFIS models for prediction of swell potential of clayey soils[J]. Expert Systems with Applications, 2011, 38(5): 5958−5966.

[30] DAS B, GANGULY U P, BAR N, DAS S K. Holdup prediction in inverse fluidization using non-Newtonian pseudoplastic liquids: Empirical correlation and ANN modeling[J]. Powder Technology, 2015, 273: 83−90.

[31] BROOMHEAD DS, LOWE D. Multivariable functional interpolation and adaptive networks[J]. Complex Systems, 1988, 2(3): 321−355.

[32] 焦李成, 杨淑媛, 刘 芳, 王士刚, 冯志玺. 神经网络七十年: 回顾与展望[J]. 计算机学报, 2016, 39(8): 1697−1716. JIAO Li-cheng, YANG Shu-yuan, LIU Fang, WANG Shi-gang, FENG Zhi-xi. Seventy years beyong neural networks: Retrospect and prospect[J]. Chinese Journal of Computers, 2016, 39(8): 1697−1716.

[33] CHEN S, COWAN C F N, GRANT P M. Orthogonal least squares learning algorithm for radial basis function networks[J]. IEEE Transactions on Neural Networks, 1991, 2(2): 302−309.

[34] PANI A K, MOHANTA H K. Online monitoring of cement clinker quality using multivariate statistics and Takagi- Sugeno fuzzy-inference technique[J]. Control Engineering Practice, 2016, 57: 1−17.

[35] GRIMA A P, WYPYCH P W. Discrete element simulations of granular pile formation Method for calibrating discrete element models[J]. Engineering Computations, 2011, 28(3): 314−339.

[36] WENSRICH C M, KATTERFELD A. Rolling friction as a technique for modelling particle shape in DEM[J]. Powder Technology, 2012, 217: 409−417.

Data driven intelligent modeling method for angle of repose of non-spherical discrete particles

HU Zhou, LIU Xiao-yan, WU Wei-ning

(College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)

The discrete element method (DEM) simulation of the angle of repose (AoR) of non-spherical is computationally intensive and time consuming. Based on the obtained DEM simulation data, the data driven intelligent modeling methods—the BP neural network and RBF neural networ were used to model the AoR of non-spherical discrete particles, and were compared with the traditional Kriging regression methods. The results show that the speed of the intelligent models is dramatically faster than the speed of the DEM simulation; the intelligent model has better predictive performance than the traditional Kriging regression model, and the BP neural network model has the best overall performance. Finally, based on the BP neural network model, the influences of particle shape and friction coefficient on the AoR were analyzed. It is found that the AoR increases with the increase of particle shape variable and friction coefficient, which further indicates the credibility of the intelligent model.

non-spherical discrete particles; angle of repose; intelligent model; discrete element method

Projects(61973108, 61374149) supported by the National Natural Science Foundation of China

2019-02-22;

2019-11-09

LIU Xiao-yan; Tel: +86-731-88822224; E-mail: xiaoyan.liu@hnu.edu.cn

1004-0609(2020)-01-0227-08

TF04

A

10.11817/j.ysxb.1004.0609.2020-36347

国家自然科学基金资助项目(61973108，61374149)

2019-02-22；

2019-11- 09

刘小燕，教授，博士；电话：0731-88822224；E-mail：xiaoyan.liu@hnu.edu.cn

(编辑 何学锋)