Reduction of wave impact on seashore as well as seawall by floating structure and bottom topography *
2020-04-02AmandeepKaurMartha
Amandeep Kaur, S. C. Martha
Department of Mathematics, Indian Institute of Technology Ropar, Rupnagar, Punjab, India
Abstract: The three-dimensional problem involving diffraction of water wave by a finite floating rigid dock over an arbitrary bottom is studied for two cases (1) in the absence of wall (2) in the presence of wall. The problem is handled for its solution with the aid of step method. Here both asymmetric and symmetric arbitrary bottom profile is approximated using successive steps. Step approximation helps to apply the matched eigenfunction expansion method, in result, system of algebraic equations are obtained which are solved to determine the hydrodynamic quantities, namely, force experienced by rigid floating dock as well as rigid seawall, free surface elevation,transmission and reflection coefficients associated with transmission and reflected waves respectively. The effects of various structural and system parameters are examined on these hydrodynamics quantities. The appropriate values of length and thickness of dock, water depth and angle of incidence provide the salient information to marine and coastal engineers to design the offshore structures and creation of parabolic trench on the bottom. The present results are compared with known results in special case of bottom topography.The energy balance relation is derived and checked.
Key words: Arbitrary bottom, step approximation, hydrodynamic quantities
Introduction
The floating structures having different geometries have been studied due to their significant applications in the field of coastal and ocean engineering.For instance, floating structures are used to implement various marine and coastal management activities such as wave energy device, breakwater, offshore platforms (for oil recovery), ship navigation and sea shore protection etc.. The problems involving scattering of surface waves by floating rigid dock over finite or infinite depth of water have been studied by many researchers using different solution techniques(see Linton[1], Chakrabarti et al.[2]and the references therein). The interaction of oblique incident waves with a horizontal flexible membrane, in finite depth of water was investigated by Cho and Kim[3]and they found that a properly designed horizontal flexible membrane can be an effective wave barrier. These structures are constructed along the shoreline with the assumption that seabed is of uniform flat type. But it is often difficult to find flat bed around the shoreline,hence sudden change in the bottom topography needs to be considered which plays significant role in designing and construction of coastal structures. In this context, the problems of wave scattering in the presence of a small undulation on seabed have been studied by many researchers: Martha and Bora[4]and many others. They used the perturbation technique due to the smallness of the bottom undulations. When the undulation is not small, such problems can be handled using mild-slope approximation[5]. Further,the problem involving linear long-wave reflection by an obstacle of general trapezoidal shape was explored by Lin and Liu[6]. They found the closed-form expression in terms of first and second kinds of Bessel functions for the wave reflection coefficient. The problem of linear long-wave reflection by a rectangular obstacle with two scour trenches has been explored by Xie et al.[7]. They found that zero reflection exists for a rectangular obstacle as long as the bathymetry is symmetrical. Moreover, Wang and Meylan[8]used boundary element method to study the problem involving scattering phenomenon of water waves by a floating thin elastic plate over variable depth of water. Xu and Lu[9]provided a method involving an optimization of eigenfunction expansion to study the problem of water wave interaction with a semi-infinite elastic plate.
Further, the problems of wave structure interaction over step type bottom topography have been studied by many researchers. For example, Karmakar and Sahoo[10]studied the problem of water wave scattering for two cases (1) semi-infinite membrane,(2) finite floating membrane in the presence of single step of finite depth. They also considered the case of infinite depth. Dhillon et al.[11]studied the problem of surface water wave interaction with a rigid thin dock in the presence of a single stepped bottom topography using matched eigenfunction expansion method. The problem of wave scattering by a semi elastic plate in the presence of step was studied by Guo et al.[12]. The problem of diffraction of obliquely incident water waves by a vertical porous structure placed over stepped bottom topography was studied by Das and Bora[13]. Meng and Lu[14]investigated the reflection and transmission coefficients for scattering of freesurface gravity wave by a porous rectangular barrier mounted on seabed by using inner product method. In the recent experimental study by Zhao et al.[15], it is found that the surface elevation at the front face of an offshore structure can reach up to four times the incident wave amplitude even in random sea state.Based on the above studies, to protect the seashore, it is important to consider the problem involving diffraction of obliquely incident water waves by thick floating structure over arbitrary bottom, which have been studied in this paper.
Moreover, it has been seen that the rigid vertical seawall is constructed near the shoreline to protect the back-land. In some locations, potential hazard happens due to shore erosion, for example, the road or buildings near the shoreline are about to fall into water due to shore erosion. Hence, the construction of seawall provides an alternative approach for coastal protection. Further, it may be noted that due to high wave impact, the sea wall may collapse. These high waves will not only affect the seawall but also move the sand away from the base of the seawall. Hence,the structural safety and stability of the seawall should be considered while designing the offshore structures.In this direction, Liu et al.[16]studied the problem of wave interaction with a perforated breakwater for reduction of wave reflection and wave force on seawall. Further, they studied the problem involving interaction between obliquely incident waves and an infinite array of multi-chamber perforated caissons and developed an analytical solution by using matched eigenfunction expansion method[17]. The problem of wave trapping by different structures over flat or step type bottom has been studied by many authors. For example, Bhattacharjee and Soares[18]studied the problem of wave-structure interaction in the presence of wall over a single step bottom topography using matched eigenfunction expansion method. The problem of wave trapping by porous barrier in the presence of step type bottom is examined by Behera et al.[19]by using modified mild-slope equation and eigenfunction expansion method. Further, the problem of wave trapping by permeable membrane located near a wall was studied by Koley et al.[20]. In most of these studies, the seawall is protected by considering thin vertical structure over flat bed or step type bottom.Hence, by placing a floating structure at a finite distance from the seawall and constructing submarine parabolic trench at the bottom bed, will create a calm zone by reducing the transmission of wave energy and this will provide an alternate solution in reduction of high wave impact on seawall as well as on seashore.To the authors’ knowledge, the literature related to thick rigid floating structure over arbitrary bottom is very limited. In the present paper, we have made an effort to study the way to protect sea shore and/or seawall by placing a rigid floating thick structure over an arbitrary bottom. The arbitrary bottom asymmetric or symmetric in nature can be approximated by successive flat shelves by which the method of eigenfunction expansion is well applicable (rather than applying a numerical method). This process yields a system of equations which is solved to determine the numerical values of transmission and reflection coefficients associated with the original boundary value problem for a few arbitrary profiles such as parabolic, triangular, trapezoidal and rectangular bottom. In addition to this, free surface elevation profiles, vertical and horizontal components of the force experienced by the floating rigid dock as well as rigid wall are examined for various values of structural and system parameters in the case of arbitrary bottom, especially for the parabolic profile.Present results are validated by comparing with the known results, which reveals an excellent agreement with the results for particular case of bottom topography. The energy identity is derived and verified.
1. Mathematical formulation of the problem
The three-dimensional problem of water wave interaction with a floating rigid dock over arbitrary bottom topography is considered for two cases: (1) in the absence of wall, (2) in the presence of wall. The dock situated at the free surface has finite length and thickness. The arbitrary bottom topography is approximated by a series of steps. Here y-axis is chosen vertically downward and xy-horizontal plane is taken to be an undisturbed free surface of water in the Cartesian coordinate system.
1.1 In the absence of wall
It is assumed that the floating rigid dock has length 2l and thickness d and it is situated at the free surface with position y=0, -l≤x≤l It is assumed that the floating structure is infinitely long in the z-direction and hence the characteristic behavior remains the same in the z-direction. Here, an asymmetric arbitrary bottom topography is taken (see Fig. 1) and is described by y=H(x), where H(x)=h(x), -a≤x≤a with a<l and H(x)=h0, x≤-a and H(x)=, x≥a.




Fig. 1 Schematic of physical problem


1.2 Method of solution

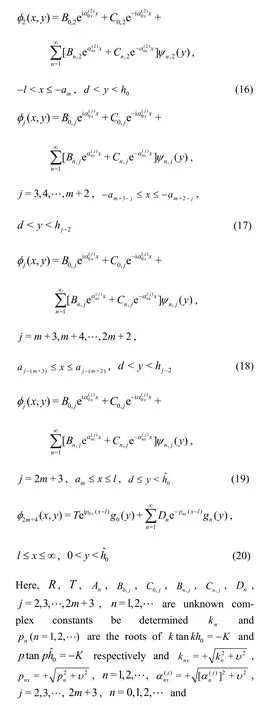




1.3 In the presence of wall
In this section, the problem of wave-structure interaction over arbitrary bottom topography is considered when a vertical rigid wall is situated at x=L as shown in Fig. 2. The regions from R1to R2m+3are same as defined in Section 1.1 “In absence of wall” and the last region R2m+4is l≤x≤L,0≤y≤Here, the associated mixed boundary value problem (BVP) will remain same as discussed in section “In absence of wall”. In addition to this, we will have a condition on the wall. Due to the rigidity of the vertical wall, the boundary condition at x=L will be

Now, we will follow the eigenfunction expansion procedure as discussed in Section 1.2 to solve the bvp involving Eqs. (1)-(14) and (39). Once φj,j=1,2,…,2m+4 are obtained, the force on the wall in the presence of rigid dock, towards the reduction of high wave load on the wall, can be calculated which is the main concern here. The expressions for velocity potentials φj, j=1,2,…,2m+3 remain the same as defined in Eqs. (15)-(30), but the velocity potential φ2m+4becomes
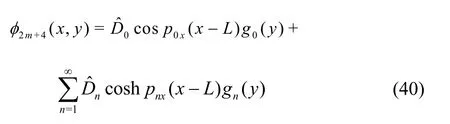
1.4 Force exercised by the floating dock and wall
The force components involving horizontal force Fxand vertical force Fyexercised by the floating dock (with and without wall) for unit amplitude incident wave are of the forms:
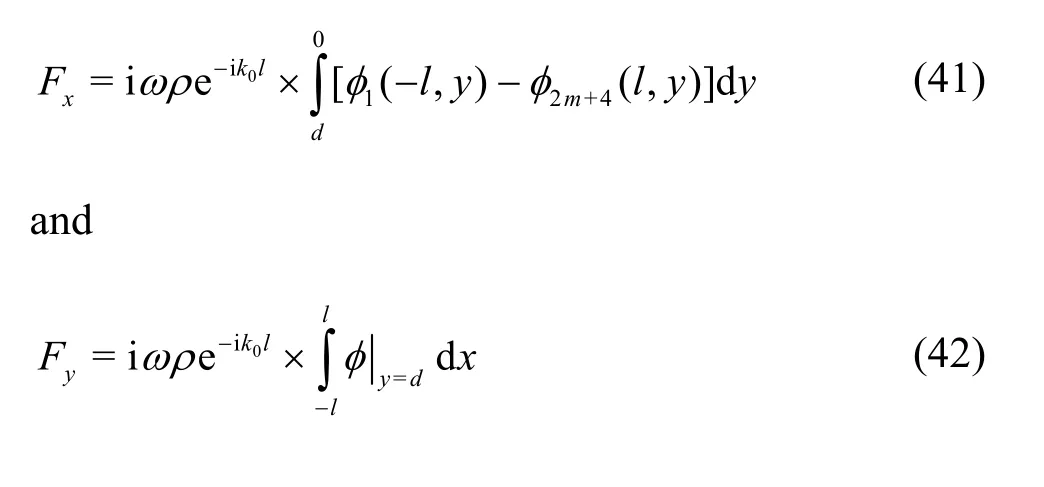
The force namely the horizontal force Fwallexperienced by the wall is derived as
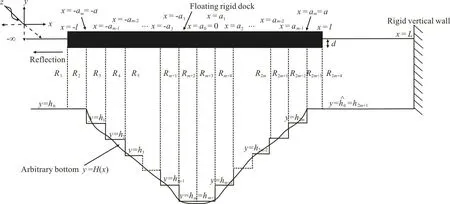
Fig. 2 Physical problem in the presence of wall

2. Results and discussion
2.1 In the absence of wall


Fig. 3 Finite rigid dock over flat bottom
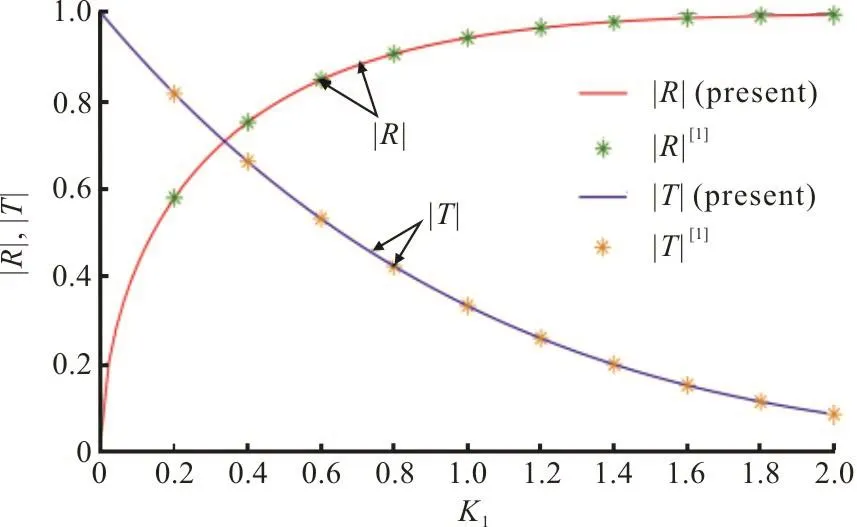
Fig. 4 (Color online)R andT versus K1 for fixed Hj =1, j=0,1,…,2m+1
2.1.2 Convergence study on m and N

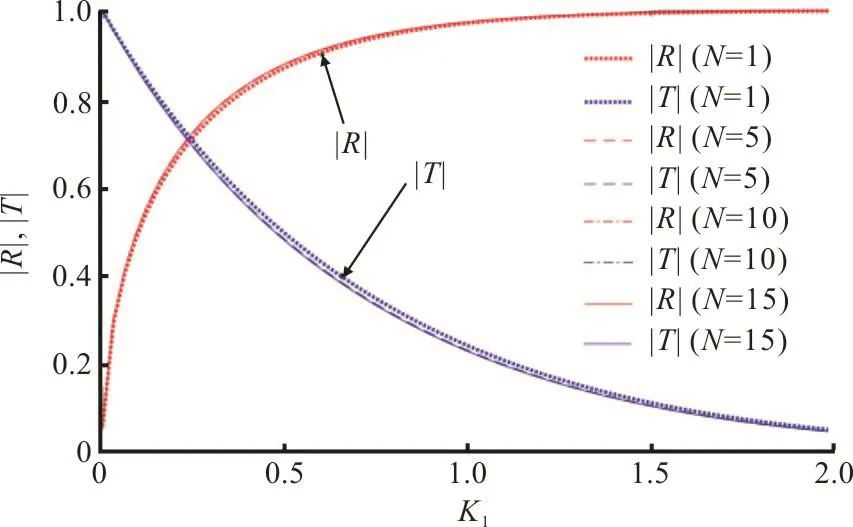
Fig. 5 (Color online)R andT versus K1 for fixed value of m=240 and different values of N


Fig. 6(a) Finite rigid dock over asymmetric parabolic bottom
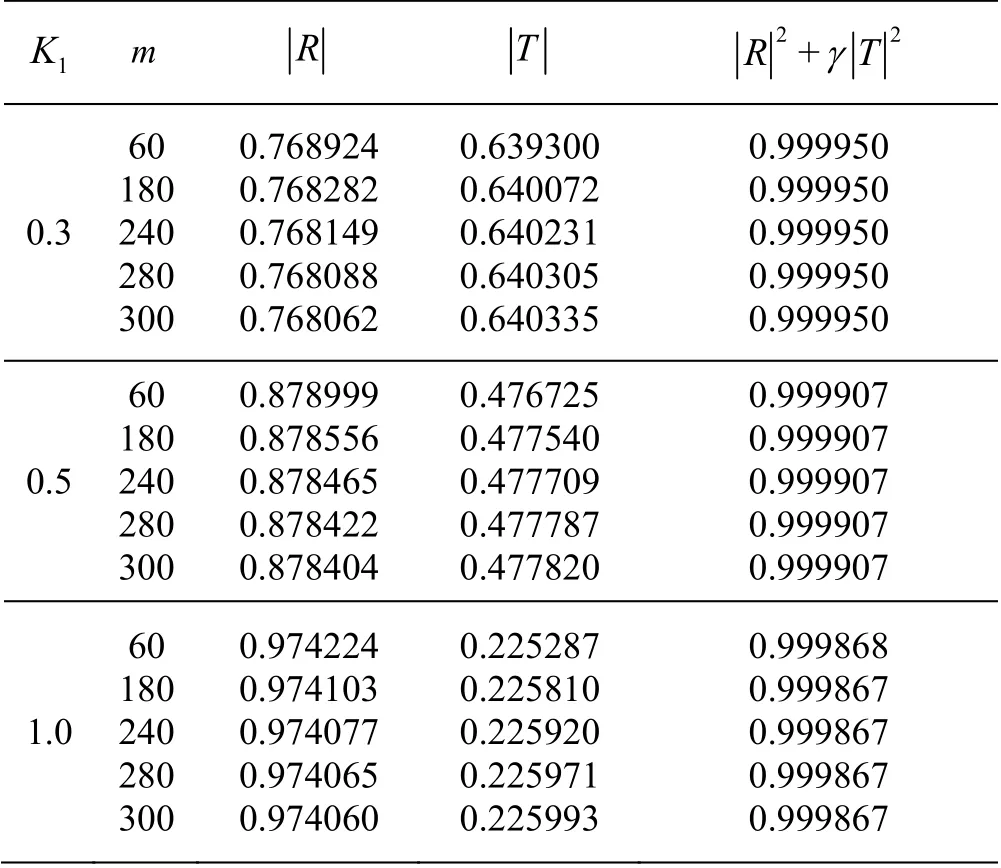
Table 1 Numerical values of Rand T versus K1 for N=10 and different values of m

2.1.3 Energy conservation principle

2.1.4 Reflection and transmission by a rigid dock over different bottom
In this section, we consider four kinds of asymmetric bottom topography namely parabolic type(Fig. 6(a)), trapezoidal trench (Fig. 6(b)), rectangular trench (Fig. 7(a)), triangular trench (Fig. 7(b)). The equations for parabolic trench, trapezoidal trench and triangular trench are given by Eqs. (46)-(48)respectively:

(1) Effect due to absence and presence of dock over rectangular bottom


Fig. 6(b) Finite rigid dock over asymmetric trapezoidal bottom
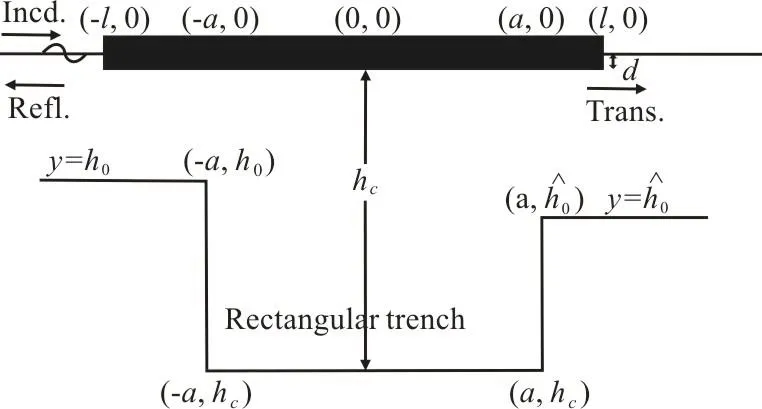
Fig. 7(a) Finite rigid dock over asymmetric rectangular bottom
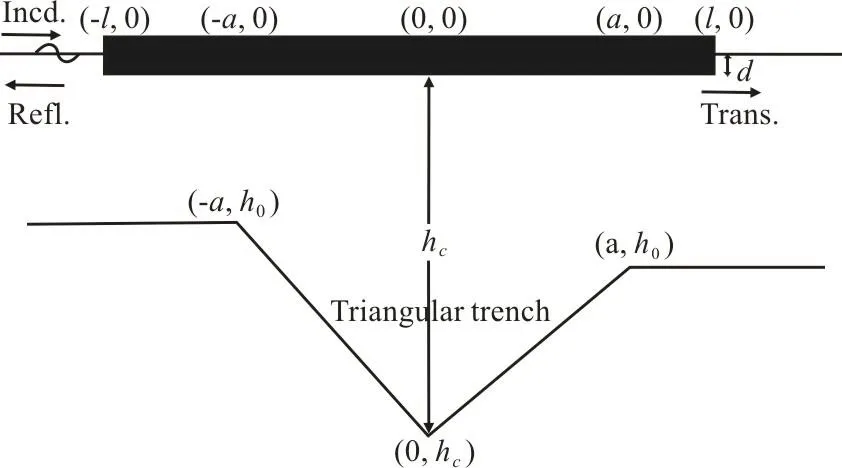
Fig. 7(b) Finite rigid dock over asymmetric triangular bottom


Fig. 8(a) (Color online)RandTin absence and presence of dock over rectangular bottom
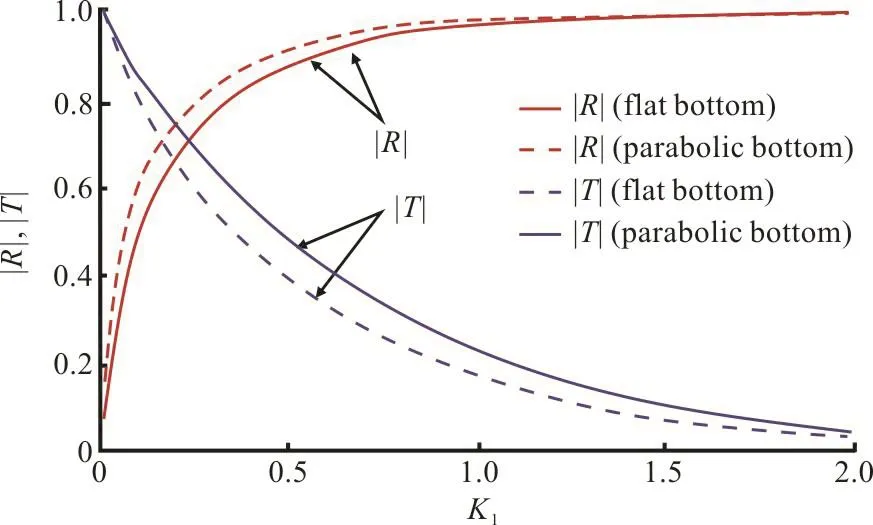
Fig. 8(b) (Color online)RandT in presence of dock over flat and parabolic bottom


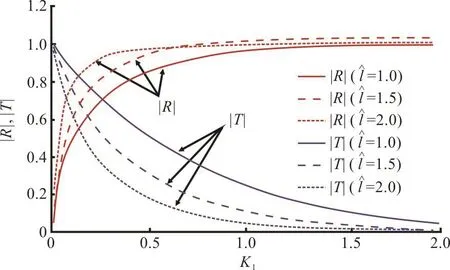
Fig. 9(a) (Color online) The effect of dock length on Rand T
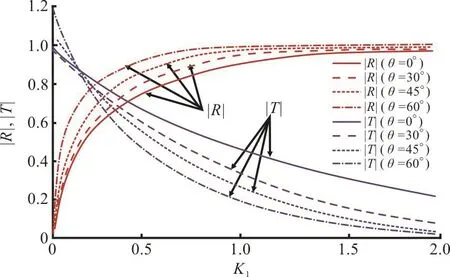
Fig. 9(b) (Color online) The effect of angle of incidence on RandT


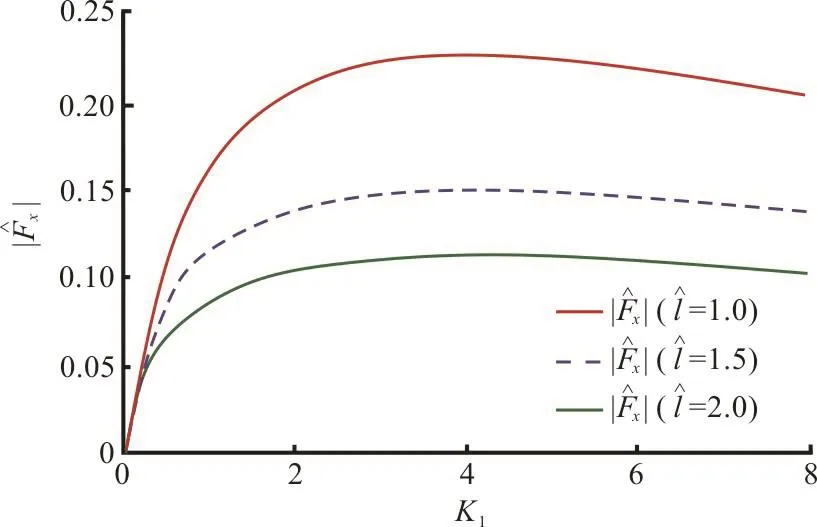
Fig. 10(a) (Color online) Effect of dock length on horizontal force () against K1
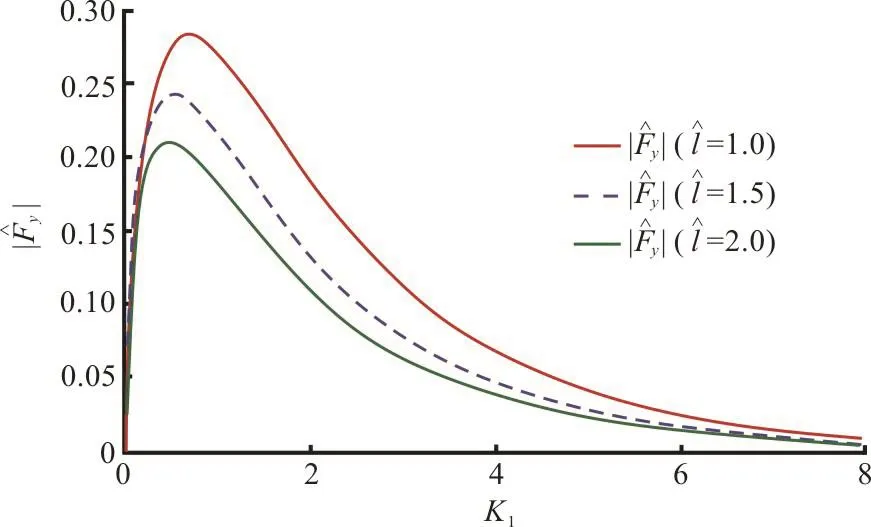
Fig. 10(b) (Color online) Effect of dock length on vertical force() against K1

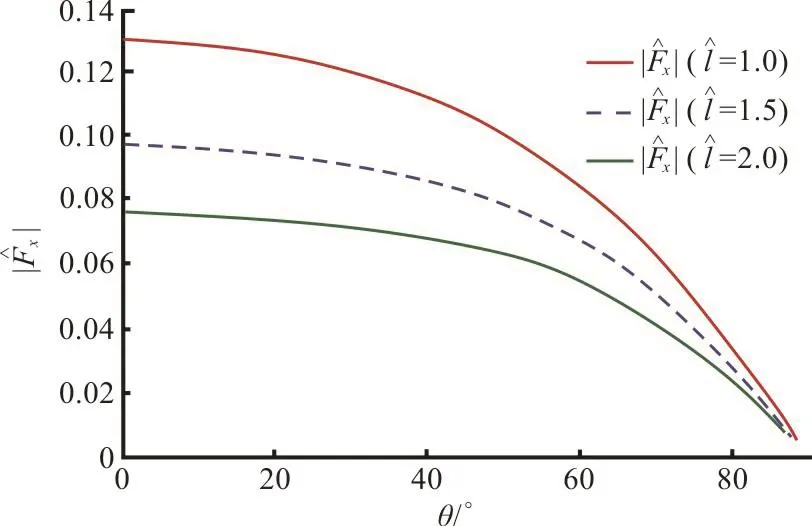
Fig. 11(a) (Color online) Effect of dock length on horizontal force against θ

Fig. 11(b) (Color online) Effect of dock length on vertical force against θ
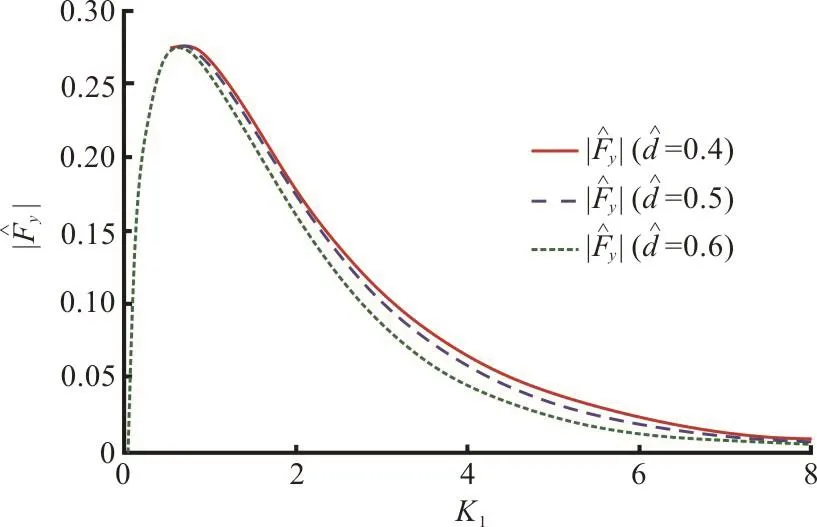
Fig. 12(a) (Color online) Effect of dock thickness on vertical force

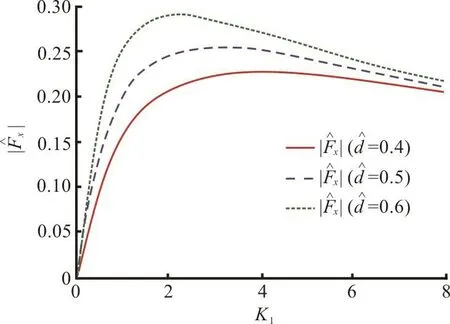
Fig. 12(b) (Color online) Effect of dock thickness on horizontal force
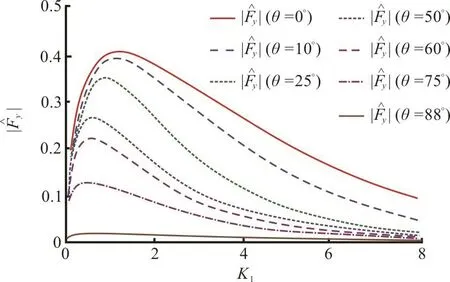
Fig. 13(a) (Color online) Effect of angle of incidence on vertical force

Fig. 13(b) (Color online) Effect of angle of incidence on horizontal force
(2) Effect of parabolic bottom profile and 60°, 75°, 88° are considered to examine the effect.It is observed that the global maximum of the force component is very small for θ=88° as compared to other angles of incidence. This happens due to the fact that for θ=88° the incident waves are almost perpendicular to the dock.
(4) Wave elevation profile in last region R2m+4
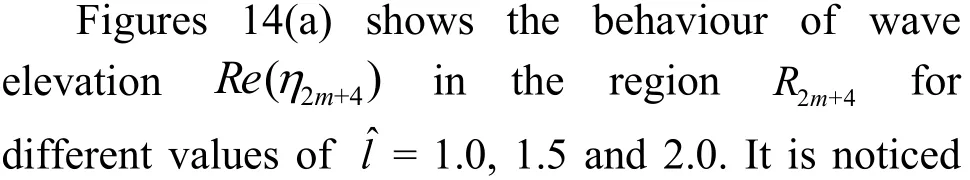

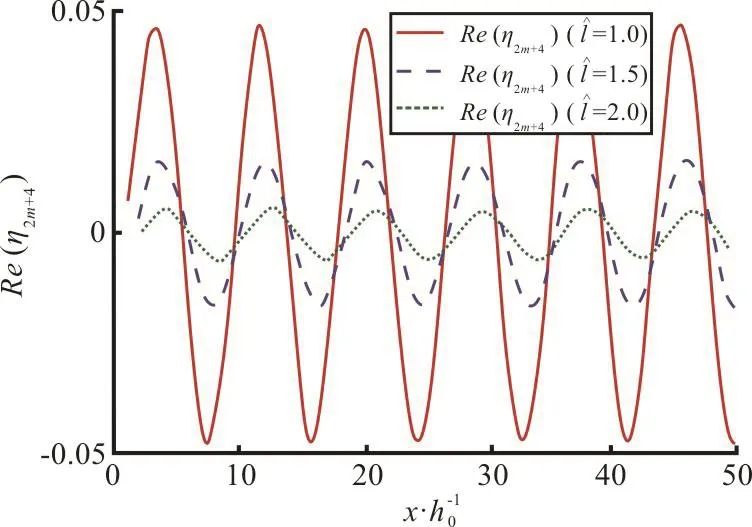
Fig. 14(a) (Color online) Effect of dock length on wave elevation Re(η2m+4) in last region for fixed K1=0.5
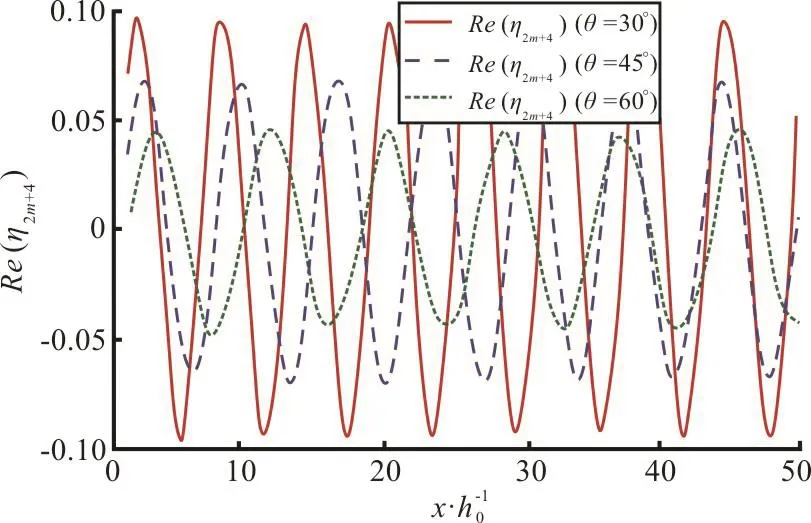
Fig. 14(b) (Color online) Effect of angle of incidence θ on wave elevation Re(η2m+4) in last region for fixed K1=0.5
2.2 In the presence of wall

fixed throughout this section unless otherwise stated.
Here our aim is to analysis how much force will be experienced by the seawall for different values of system parameters so that the seawall can be protected.It is natural that there will be full reflection and no transmission due to the presence of seawall.
(1) Effect of dock and parabolic bottom topography on seawall



Fig. 15 (Color online) Horizontal force over flat and parabolic bottom in presence of dock
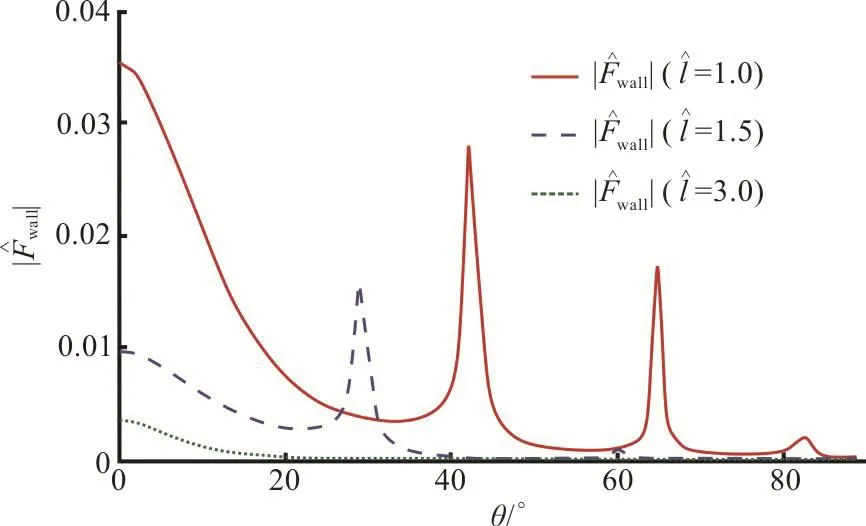
Fig. 16(a) (Color online) Effect of dock length on
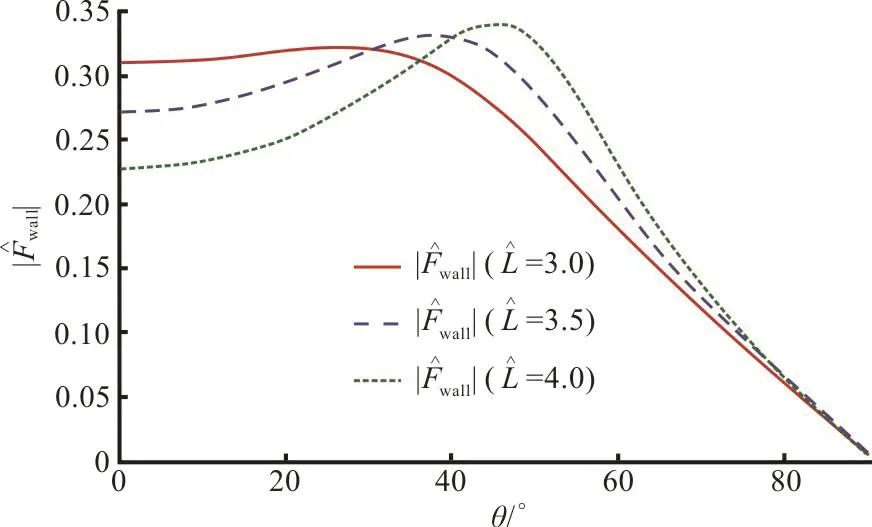
Fig. 16(b) (Color online) Effect of gap between seawall anddock on
3. Conclusions

Fig. 17 (Color online) Wave elevation Re(η1) in presence of wall for fixed K1=1.0
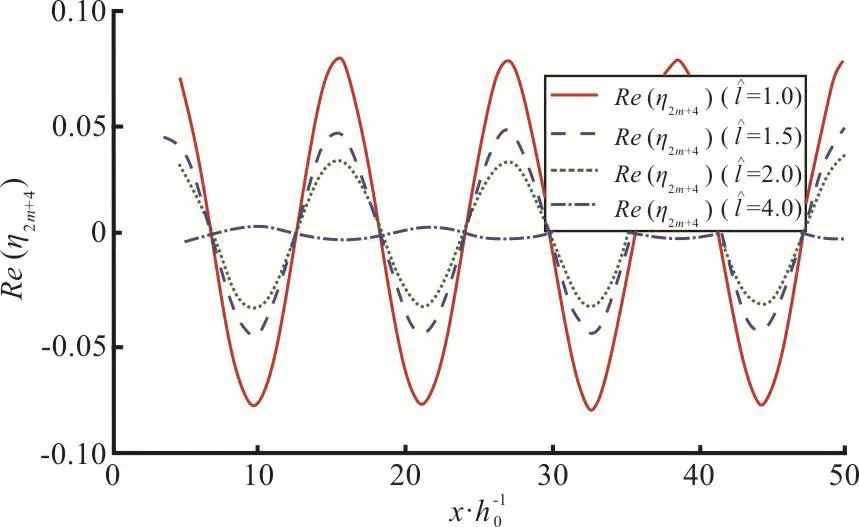
Fig. 18(a) (Color online) Effect of dock length on wave elevation Re(η2m+4) for fixed K1=1.0

Fig. 18(b) (Color online) Effect of gap onwave elevation Re(η2m+4) for fixed K1=1.0
The three-dimensional problem involving diffraction of water waves by a finite floating thick rigid dock over an arbitrary bed is studied for two cases (1)in the absence of wall, (2) in the presence of wall. The uneven shape is approximated by a series of steps for which m number of steps are taken in downward direction and m number of steps is taken in upward direction. The step approximation followed by matched eigenfunction expansion method yields a system of equations, which is solved to determine the numerical values of hydrodynamic quantities. The effect of various structural parameters, such as length,thickness of dock and gap between dock and seawall,water depth and angle of incidence on the reflection,transmission and force is examined through different graphs. In the absence of wall the present results have been validated by the known results[1]. The energy identity is checked which verifies the accuracy of numerical results.

In the presence of wall: (1) Less horizontal force on seawall is experienced when the dock is situated over the parabolic bottom instead of flat bottom for oblique wave incidence. (2) Since more incidents wave energy is reflected back by longer the length as well as the thickness of the dock, hence, less force is experienced by seawall. (3) By placing a floating structure at a finite distance from the seawall, the high wave load on the seawall can be reduced. (4) If the gap between the seawall and dock is least then more force is experienced by the seawall for smaller values of θ whereas reverse behavior of force is observed for larger value of θ. Hence, the length and thickness of the dock, gap between the dock and seawall, angle of incidence and water depth can be modified to optimize the wave load on the rigid seawall. (5) It is observed that wave amplitude in the last region decreases as the length of the dock, the thickness of the dock, gap between the seawall and dock, water depth increases. Moreover, the wave amplitude in the last region (after the dock) is very small as compared to amplitude in the first region (before the dock). This provides a tranquillity zone between the floating dock and the rigid seawall, which is useful for the harbour areas (for example, the calm zone will provide a safe mooring-loading operations and comfortable handling of cargoes and ships). This study will provide an immense support to coastal engineers for the construction of offshore structures so that seashore as well as seawall can be protected.
Acknowledgment
The authors thank the reviewers and associate editor of Journal of Hydrodynamics for their comments and suggestions to improve the article in the present form. A. Kaur thanks DST, India for support through inspire fellowship.
杂志排行
水动力学研究与进展 B辑的其它文章
- Liutex core line and POD analysis on hairpin vortex formation in natural flow transition *
- Numerical study on the bubble dynamics in a broken confined domain *
- Flow characteristics in open channels with aquatic rigid vegetation *
- A study of the evolution of nanoparticle dynamics in a homogeneous isotropic turbulence flow via a DNS-TEMOM method *
- Numerical investigation on the drag force of a single bubble and bubble swarm *
- Local scour by multiple slit-type energy dissipaters *
