A study of the evolution of nanoparticle dynamics in a homogeneous isotropic turbulence flow via a DNS-TEMOM method *
2020-04-02HongyeMaMingzhouYuHanhuiJin
Hong-ye Ma, Ming-zhou Yu, Han-hui Jin
1. College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China
2. Institute of Fluid Engineering, Zhejiang University, Hangzhou 310027, China
Abstract: In this article, a coupling of the direct numerical simulation (DNS) and the population balance modeling (PBM) is implemented to study the effect of turbulence on nanoparticle dynamics in homogenous isotropic turbulence (HIT). The DNS is implemented based on a pseudo-spectral method and the PBM is implemented using the Taylor-series expansion method of moments.The result verifies that coagulation due to turbulent shear force has a bigger impact on the evolution of number concentration,polydispersity, and average diameter of nanoparticles than Brownian coagulation in the HIT. The Reynolds number plays an important role in determining the number concentration, polydispersity, and average diameter of nanoparticles, and these quantities change more rapidly with an increase of Reynolds number. It is also found that the initial geometric standard deviation slows down the evolution of particle dynamics, but almost has no influence on the polydispersity of nanoparticles.
Key words: Nanoparticle dynamics, turbulence, pseudo-spectral method, Taylor-series expansion method of moments
Introduction
Because of good physical and chemical properties, nanoparticles are widely used in various branches of industry, such as the material, chemical, metallurgical, aerosol, etc.. During the formation and preparation of nanoparticles, a two-phase nanoparticle-laden flow system, such as gas-solid two-phase flow or solid-liquid two-phase flow, exists[1]. The main feature of such systems is their polydispersities in particle size[2], and correspondingly the Smoluchowski mean-field theory has been the fundamental theory for studying them[3]. The key to this theory is its general but powerful governing equation (i.e., the population balance equation (PBE))[4]The PBE is an integraldifferential Fokker-Planck equation that considers the particle number intensity, and it can provide details of the evolution of the aerosol size distribution and statistical quantities, such as the total particle number and volume concentration, over time[5]. Because of the inherent property of the Fokker-Planck equation, the PBE has an advantage of coupling to computational fluid dynamics (CFD) within an Eulerian-Eulerian framework. The methodology that couples the PBE and CFD is widely regarded as the population balance modeling (PBM), which has played an increasingly crucial role in both environmental and chemical engineering now[6-8].
During the implementation of the PBM, the two-way coupling between the continuum and the dispersed phases is a priority recommendation. Under the condition of turbulent flows, the effect of turbulence on the particle dynamics should be properly described by the coupled governing equations[9].Unfortunately, such effects of turbulence on the particle dynamics are usually ignored in most models of the PBM[6]. This is because there are no suitable mathematical models to characterize the effect of fluid turbulence on the particle dynamics, i.e., the turbulent fluctuation terms of transport equations for dispersed phase cannot be modeled[4,9]. Garrick and his group are the first to study the effect of turbulence on nanoparticle dynamics including nucleation, condensation, and coagulation[10-11]. In their studies, the highly accurate direct numerical simulation was utilized to isolate the effect of the small or subgridscale particle-particle interaction in the threedimensional jet or boundary flows. The aim is to capture the small, unresolved or subgrid-scale particle-particle interaction when Reynolds-averaged Navier-Stokes simulations (RANS) or large eddy simulation (LES) is utilized. Regardless of jet or boundary flows, they are problem-specific solutions,and thus the obtained closure model from the direct numerical simulation (DNS) for the dispersed phase cannot be directly extended to other cases. A more appropriate way to get a generalized closure model for nanoparticle dynamics affected by turbulence is the study under a HIT condition, which was used by Moody and Collins to study titania nanoparticle nucleation and growth in a turbulent “box” located near the center of the reactor via three-dimensional DNS coupled with moment method[12]. However, in this study, no further details about the relative importance of Brownian coagulation and turbulent coagulation to the evolution of nanoparticle dynamics are revealed.
Nowadays, in almost population balance models for chemical processes and environmental aerosols[7-8,13-14],Brownian coagulation is usually the only dyna- mics considered. This might be reasonable where turbulence plays no or very little role in the evolution of multiphase flows. However, as the turbulent intensity is stronger which not only affects the flow structure but also affects the dispersed particles’dynamics, the ignorance of the effect of turbulence on coagulation becomes unreasonable. The effect of turbulence on coagulation can be divided into two aspects: one is the enhancement of Brownian coagulation due to strong mixing[9], another is turbulent coagulation due to shear forces[4,15]. Under some turbulent flows, the coagulation due to turbulence shear force might be stronger than that due to particle Brownian motion[16-17]. Unfortunately, to our knowledge, no systemic studies are carried out to study the difference between Brownian coagulation and turbulent coagulation under a specific turbulent flow.
The coupling between the Navier-Stokes equations and population balance equations for the study of nanoparticle dynamics is not new, which has been widely utilized by researchers to study the fundamentals of nanoparticle dynamics in a simple turbulent condition and to investigate the engineering processes in the field of chemical engineering and atmospheric aerosol processes[7-8,17-18]. Here, the population balance equations cannot be directly coupled to the Naver-Stokes equations due to its too many degrees in terms of particle size[19]. The feasible scheme to resolve the problem is to convert the population balance equation to a set of equations with respect to moments. The scheme is called the method of moments (MOM). Several effective closure techniques have been proposed to obtain the moment equations: the predefined size distributed method such as log-normal MOM (logMOM)[20]and Gamma MOM[21], quadrature-based moment method (QBMM)such as quadrature method of moments (QMOM) and direct QMOM[22-23], pth-order-polynomial MOM[24],MOM with interpolative closure (MOMIC)[25], and Taylor series expansion MOM[26]. Although all these MOMs have been utilized to couple with the Navier-Stokes equations, the study of nanoparticle dynamics considering Brownian coagulation and turbulent coagulation under homogeneous isotropic turbulence is unavailable.
In the work of Liu and Lin[7]and Lin et al.[17], the coupling between the Navier-Stokes equations and population balance equations is successfully applied to the study of nanoparticle coagulation in a pipe flow.In their study, the population balance equation is solved with the logMOM or TEMOM, which is verified to be a very promising scheme for such problems. In the work of Lin et al.[17], the effect of turbulent coagulation due to shear force on nanoparticle evolution is considered in a pipe flow. In this article, however, the coupling between the Navier-Stokes equation and the population balance equation is carried out by implementing a pseudo-spectral method and TEMOM model. Both Brownian coagulation and turbulent coagulation can be studied over the whole flow scales, with that the comparison of the effect of Brownian coagulation and turbulent coagulation on nanoparticle dynamics can be done under the same condition. Since particles considered in this study are small, whose Stokes number is far less than 1, only one-way coupling between phases is considered.
1. Mathematical formulation
1.1 Flow field
In the present work, the flow is assumed to be of constant density and constant temperature. No forcing function is applied to the Navier-Stokes equation,meaning a decaying homogenous isotropic turbulence is studied. The equations governing the motion of the above-described fluid in a box are:


where A is a constant, the initial energy spectrum is the range of ka, kb, and it determines the initial total kinetic energy in the simulation. The velocity spectrum can be determined according to the energy spectrum[27]

are random coefficients,1θ,2θ, φ are random numbers with uniform probability density between{0,2π}. According to the theory of the turbulence, u′is the root-mean-square (rms), Ω(t) is the vorticity pseudo-energy, ε(t) is the turbulent energy dissipation rate, Re is the Taylor microscale Reynolds number; they can be calculated by the following formula.


1.2 Particle field
The modeling of the nanoparticle phase is based on the population balance theory, which is from the Smoluchowski mean-field theory[3]. The governing equation for determining particle size distribution with internal coordinate v and external coordinates x and t takes the following form
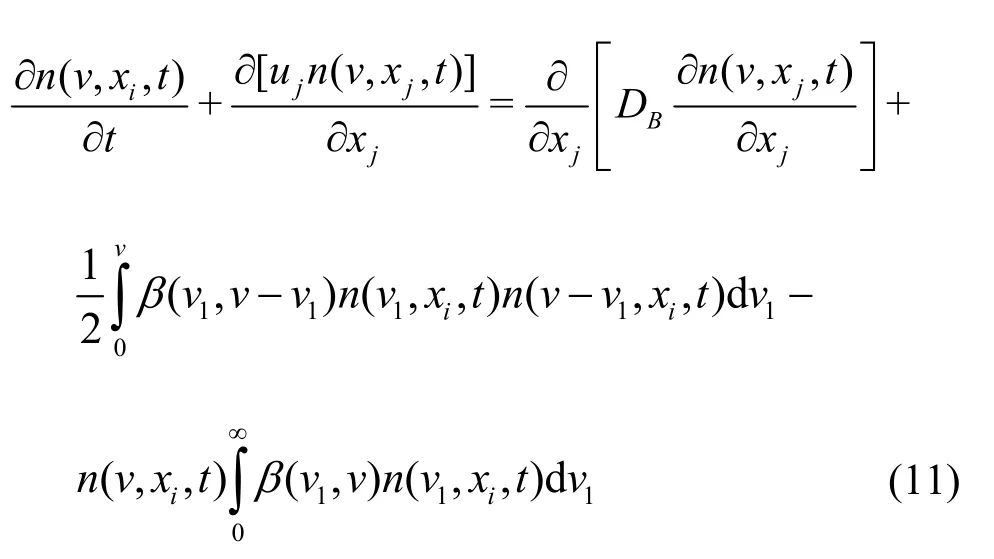
Equation (11) cannot be directly coupled to the Navier-Stokes equations due to its too much degrees for v. An alternative way is to convert Eq. (11) to a set of moment ordinary differential equations using the following definition




2. Results and discussion
2.1 Initial conditions
In the present study, all computations are carried out in a domain, 2π×2π×2π. The initial energy spectrum is given by Eq. (5). To ensure the operation of the program and the convergence of the results, the third-order precision Rung-Kutta method is used to solve the ordinary differential equations, and the dimensionless time step size Δt is fixed to be 0.00001, which ensures the CFL number always less than 1. ka=3, kb=8, ν=1.67×103, T=296,ρ=1. Moreover, some parameters used in the simulations are shown in Table 1, the initial particles are distributed at each cell. For the convenience of calculation, we set the moment to three identical values according to the flow rate. The initial m10=m20=the initial velocity magnitude/2, and the initial m00=1.0,1.5,2.0×m10.

Table1 Parameters used in the simulations
2.2 Verification
For any numerical studies, the reliability of calculated data from the numerical simulation should be ensured. To achieve this, firstly, we choose a suitable grid number to improve the precision and accuracy of frequency. When solving the equation of the first moment, the first moment m1remains unchanged because the total particle mass is constant,i.e., 1.00. We compare the evolution of the first moment m1in Fig. 1, the image shows the error of m1changing with time, the numbers of meshes is 163,323can cause a larger error, but when the number of meshes is 643, the error of m1is almost equal to zero.It shows that the reliability and precision of the simulation are improved while the grid is refined. If there are too many meshes, the computational efficiency will be decreased, therefore, the number 643can retain the computational efficiency and appropriate accuracy.

Fig. 1 (Color online) Evolution of the first moment m1
With parameters shown in Table 1, the evolution of the flow field is obtained. As shown in Figs. 2 and 3, the velocity magnitude and vorticity magnitude gradually reduced, its three-dimensional structure will influence the evolution process of the nanoparticles.Figure 4 shows the evolution of the zeroth moment m0when Brownian coagulation is involved, particle number concentration decreases with time.
2.3 Brownian coagulation and the turbulent shear coagulation
Figure 5 shows the comparison of the evolution of 0-th, 1-th and 2-th moments with time undergoing the turbulent coagulation and Brownian coagulation.In the study, the turbulent Reynolds number is 71.93 and the initial geometric standard deviation of nanoparticle number distribution is 1.00. The 0-th moment represents particle number concentration,correspondingly 2-th moment increases with time. It is clear that for both 0-th and 2-th moments, they change more quickly for turbulent coagulation than that for Brownian coagulation. The same property is also characterized by the growth of particle size with time,which is shown in Fig. 6. Under the same flow condition, turbulent coagulation leads to a higher growth rate for nanoparticles than Brownian coagulation.
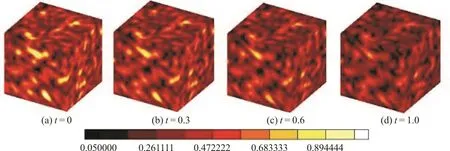
Fig. 2 (Color online) Evolution of velocity magnitude
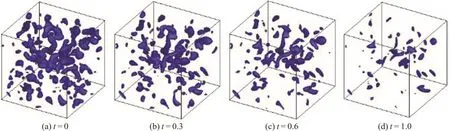
Fig. 3 (Color online) Evolution of vorticity magnitude iso-surface value is 0.3
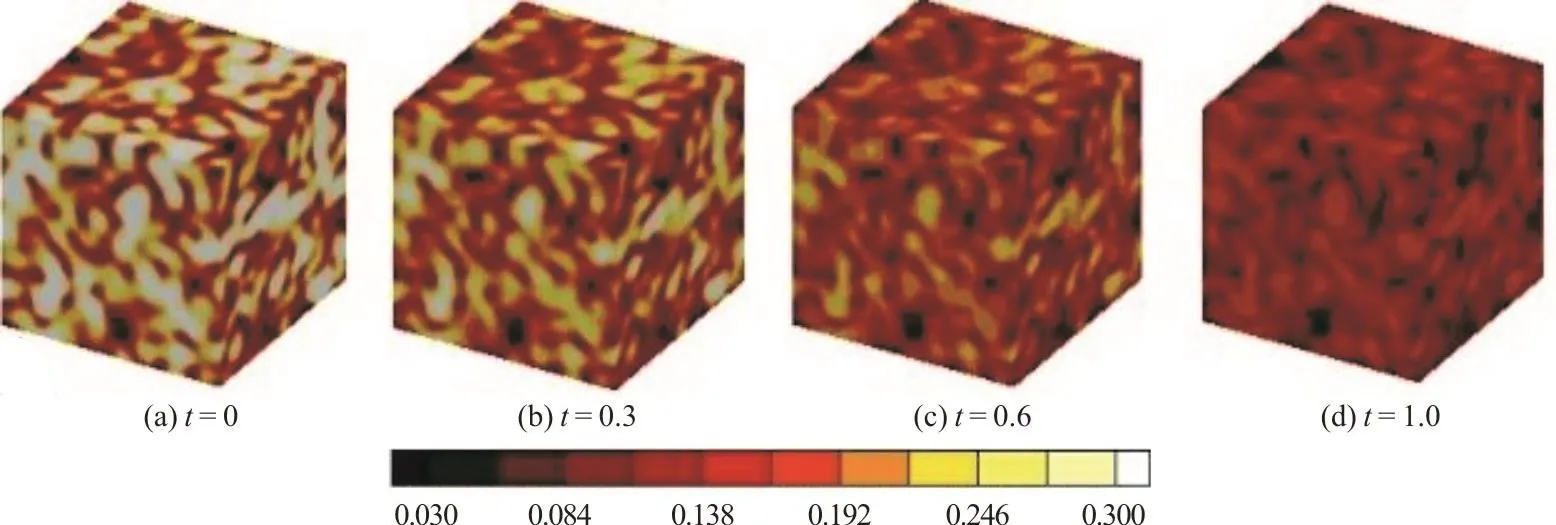
Fig. 4 (Color online) Evolution of the zeroth moment m0
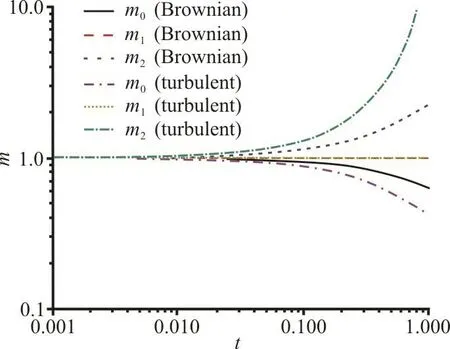
Fig. 5 (Color online) Evolution of the moments with time undergoing Brownian coagulation and turbulent coagulation
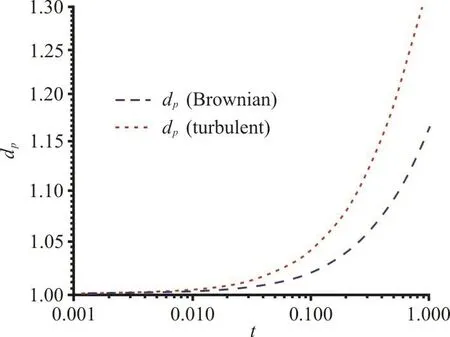
Fig. 6 (Color online) Evolution of the particle diameter with time undergoing turbulent coagulation and Brownian coagulation

Fig. 7 (Color online) Evolution of the zeroth moment m0 , secondary moment m2, and averaged particle diameter dp at turbulent shear coagulation for σg0=1.00,Re=29.24, 58.49 and 71.93
2.4 Effect of Reynolds number
In order to reveal the effects of the Reynolds number on particle size evolution, simulations for various Reynolds numbers are performed. The zeroth moment m0, the second moment m2and the average mean diameter are presented in Fig. 7. It reveals the Reynolds number plays an important role in determining the evolution of particle dynamics.With an increase of the Reynolds number, the evolution of particle number concentration, i.e., m0,drops more quickly. Correspondingly, the secondary moment and the averaged diameter increases more faster with an increase of the Reynolds number.
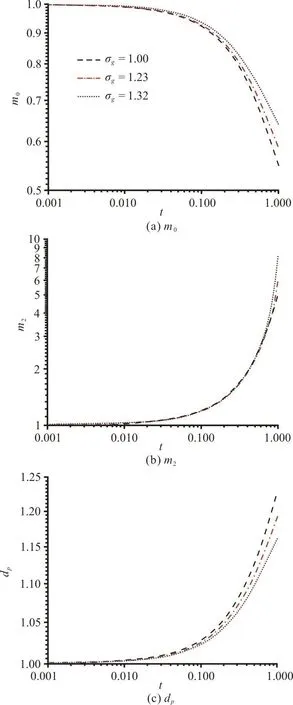
Fig. 8 (Color online) Evolution of the zeroth moment m0, secondary moment m2, and averaged particle diameter dp for Re=58.49, 1.00, 1.23 and 1.32
2.5 Effect of the initially geometric standard deviation
In order to reveal the effects of the initial geometric standard deviation σg0on particle size evolution, zeroth moment m0, the second moment m2and the average mean diameter are presented in Fig. 8. the zeroth moment m0at Re=58.49 is plotted with σg0=1.00, 1.23 and 1.32. In the decaying homogeneous isotropic turbulence, m0slow down at larger σg0that suggests the total particle number concentration increases as σg0grow.With the increase of σg0, the second moment m2almost keeps the same, this indicates σg0has no effect on the evolution of polydispersity of the nanoparticles, and the average mean diameter of particles becomes smaller as the σg0grow. This phenomenon implies that σg0slow down the evolutionary process of nanoparticle in the condition of turbulent shear coagulation.
3. Conclusion
The coupling of the direct numerical simulation and the population balance modeling is performed to study the effect of turbulence on nanoparticle dynamics. The direct numerical simulation is implemented with a pseudo-spectral method, while the population balance modeling is carried out by a Taylor-series expansion method of moments. Both Brownian coagulation and turbulent coagulation due to shear forces are considered and compared. Under the same condition, turbulent coagulation plays a more important role to determine the evolution of nanoparticle dynamics than Brownian coagulation. The effect of turbulence on nanoparticle dynamics under homogeneous isotropic turbulence is studied with varying the Reynolds number, and initial geometric standard deviation. It reveals a higher Reynolds number leads to a faster evolution of nanoparticle dynamics. However, the initially geometric standard deviation has different and even opposite effects on the evolution of nanoparticles, its increase will slowly reduce the trend of the total particle number concentration and average mean diameter, but it almost does not affect the polydispersity.
杂志排行
水动力学研究与进展 B辑的其它文章
- Liutex core line and POD analysis on hairpin vortex formation in natural flow transition *
- Numerical study on the bubble dynamics in a broken confined domain *
- Flow characteristics in open channels with aquatic rigid vegetation *
- Numerical investigation on the drag force of a single bubble and bubble swarm *
- Local scour by multiple slit-type energy dissipaters *
- Liutex-based vortex dynamics: A preliminary study *
