基于“当前”统计模型的变结构交互多模型算法

傅虹景，于守江，吉 峰，劳丹涤

(上海航天电子技术研究所，上海 201109)

0 引言

机动目标跟踪问题是现代雷达数据处理系统中的难点，原因在于目标运动方式的不确定性[1-3]。目前，卡尔曼滤波算法是目标跟踪问题中应用较为广泛的算法[4-5]，但是受限于目标的运动方式只能用单一的模型来描述。若单一的模型无法匹配目标的机动性时，通常会出现滤波器的估计精度下降，甚至发散或丢失目标的现象[6-7]。为此，基于卡尔曼滤波的多模型算法被提出[8-9]。

交互多模型(Interacting Multiple Model，IMM)算法是目前多模型算法中应用较为广泛的算法[10-12]，通过不同的模型来描述目标的运动方式，然后并行滤波，综合加权得到目标的状态估计。但是IMM算法的估计性能很大程度上依赖于所选取的模型集合，为了提高机动目标的跟踪性能，应当增加更多的模型来匹配目标的机动性，然而增加模型不仅会导致计算量增加，而且会使模型之间的竞争更加激烈，进而导致算法的估计性能下降[13]。为此，变结构IMM(Variable Structure IMM，VSIMM)算法[14]被提出，如模型组转换法[15]、自适应网格算法[16]、有向图算法[17]和期望模式扩展算法[18]等。VSIMM算法能使模型集合动态更新，相较于IMM算法有更好的自适应能力。

“当前”统计(Current Statistical，CS)模型是一种非零均值时间相关模型[19-20]，该模型认为目标下一时刻的加速度是满足修正的瑞利分布，可以跟踪机动性较强的目标，但是其性能受到最大加速度参数的影响，对于机动性较弱的目标跟踪性能较差[21-22]。本文给出了一种基于CS模型的VSIMM算法，在自适应网格IMM算法的框架下，根据加速度的一步预测结果，自适应调整CS模型中的最大加速度参数。仿真结果表明，相较于固定结构的IMM算法，VSIMM算法对目标的估计精度更高，跟踪性能更好。

1 CS模型

CS模型是一种非零均值时间相关模型，它假设目标以某一加速度机动时，下一时刻的加速度取值范围有限，而且总在“当前”加速度值的附近，所以加速度的概率密度函数用修正的瑞利分布描述：

(1)

式中，amax为目标加速度的最大值；a为目标的加速度；μ>0为一常数。

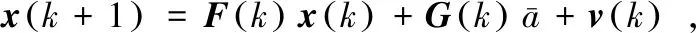
(2)

式中，x(k)为目标k时刻的状态向量；F(k)为状态转移矩阵；G(k)为输入控制矩阵；v(k)为零均值；协方差为Q(k)的过程噪声。当采用CS模型时：

(3)

(4)

(5)

(6)

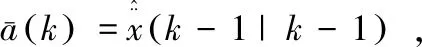
(7)

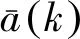
由式(6)可以看出，加速度的方差由最大加速度和当前加速度的估计值决定，而当前加速度的估计值与滤波算法有关，所以CS模型的性能依赖于机动频率和最大加速度。对于固定参数的CS模型，存在以下缺陷：

① 当amax的取值较小时，CS模型的加速度方差较小，跟踪精度较高，然而跟踪的目标加速度变化范围较小，不能及时响应快速机动；当amax的取值较大时，CS模型的加速度方差较大，可以及时响应目标较大范围的机动，但是跟踪精度有所降低。所以amax如果在跟踪过程中不能自适应调整，将影响CS模型的性能。

2 基于CS模型的VSIMM算法

本文提出的基于CS模型的VSIMM算法借鉴自适应网格IMM算法的思想，设立3种amax参数不同的CS模型，根据当前加速度的一步预测值，自适应调整下一时刻的模型参数amax，算法流程如图1所示。

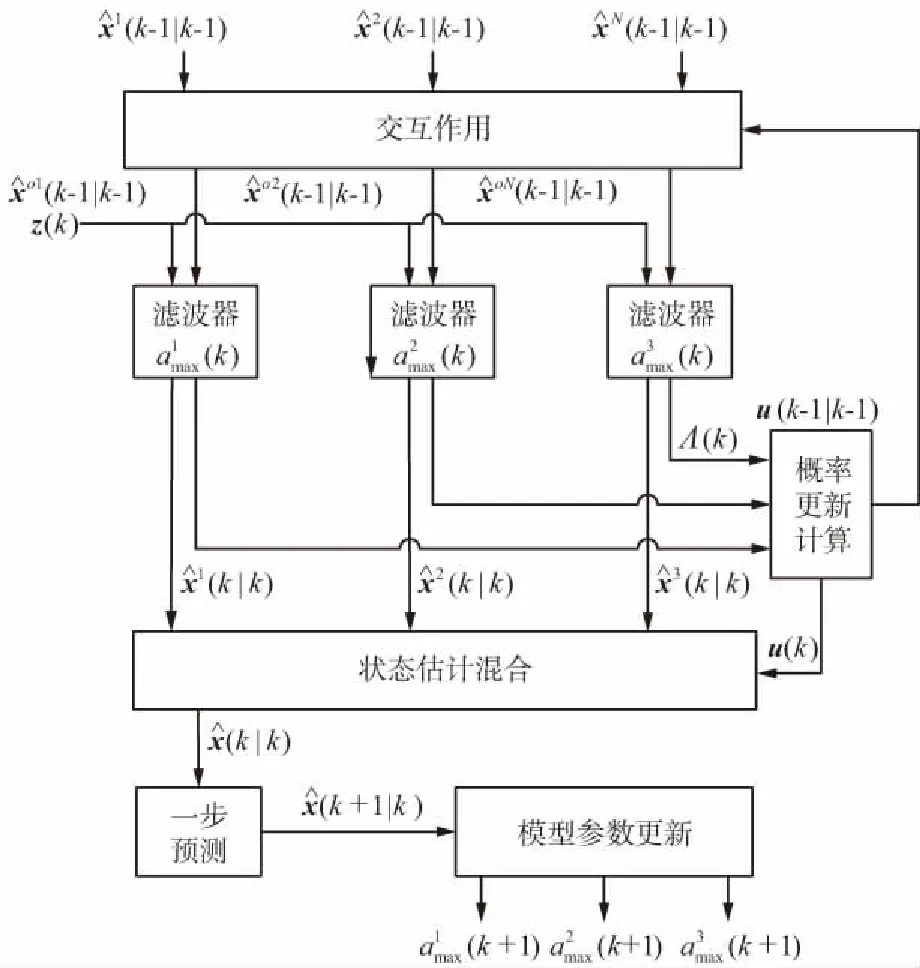
图1 基于CS模型的VSIMM算法流程Fig.1 Flow of VSIMM algorithm based on CS model

(8)

步骤1：状态估计的交互式作用

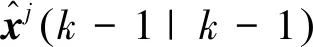
(9)

式中，

(10)

(11)

步骤2：并行卡尔曼滤波

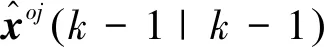
步骤3：计算模型可能性

(12)

步骤4：更新模型概率

模型j的概率更新为：

(13)

式中，

(14)

步骤5：状态混合估计

(15)

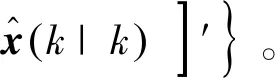
(16)

步骤6：状态向量的一步预测

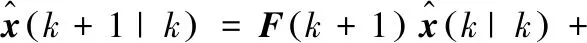
(17)

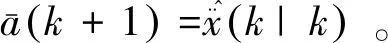
步骤7：模型参数更新

由于当前加速度的均值可以得到，那么下一时刻的加速度的取值应该在均值附近，根据状态向量的一步预测更新模型参数：

(18)

式中，σa为最小模型间隔。

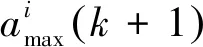
(19)

以上即为基于CS模型的VSIMM算法的全部流程。

3 算法仿真与分析

以二维场景中单个机动目标为跟踪对象，将基于CS模型的VSIMM算法与固定参数的CS模型IMM算法进行了对比。

目标运动场景：目标起始位置状态为x(0)=(0 m 10 m/s 10 m/s20 m 0 m/s 0 m/s2)T，目标的运动轨迹如图2所示。

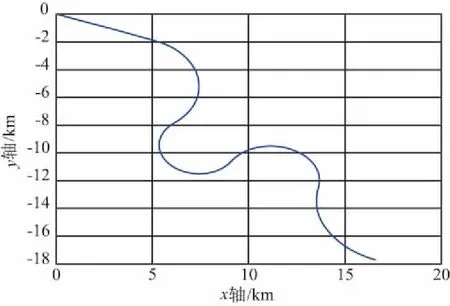
图2 二维场景中单个机动目标的运动轨迹Fig.2 Trajectory of maneuvering target in two-dimensional scenario

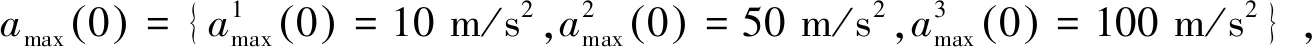
固定参数的IMM算法的参数同上。

传感器量测及其他参数：雷达的量测噪声为均值为0，方差为400 m2的高斯白噪声，采样间隔T=1 s，每次仿真步数200步。仿真结果由100次蒙特卡罗实验统计得到。

图3给出了不同跟踪算法下目标位置的均方根误差曲线，图4给出了目标速度的均方根误差曲线。由图3和图4可以看出，对于固定参数的CS模型IMM算法，其滤波结果的位置误差和速度误差相对较大，性能不如VSIMM算法。因此可以得出，对于参数自适应的CS模型VSIMM算法，目标的跟踪性能更好。

图3 目标位置均方根误差曲线Fig.3 Root mean square error of target position

图4 目标速度均方根误差曲线Fig.4 Root mean square error of target speed

4 结束语

本文针对机动目标跟踪问题，提出了一种基于当前统计模型的自适应变结构交互多模型算法，该算法根据滤波结果和状态预测信息，实时调整CS模型中是最大加速度参数，一定程度提升了CS模型对于弱机动目标的跟踪性能。仿真结果表明，该算法的位置和速度估计精度要优于固定参数的交互多模型算法。由于CS模型中另一个参数机动频率也对跟踪性能有影响，所以如何同时调整机动频率与最大加速度是下一步研究的工作。