基于TP+FPT的L2-STC-Multi-h CPM遥测系统的高可靠性检测算法
2020-04-02王西夺赖鹏辉李泰立王方刚
王西夺,赖鹏辉,李泰立,王方刚,王 岩,张 炜
(1.中国电子科技集材公司 航天信息应用技术重点实验室,河北 石家庄 050081;2.国防科技大学 电子科学学院,湖南 长沙 410073;3.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;4.北京宇航系统工程研究所,北京 100084)
0 引言
连续相位调制(Continuous Phase Modulation,CPM)信号具有恒包络特性、高功率效率和低截获率等优点,被广泛应用于航空遥测、深空通信等领域[1-2]。在遥测系统中,为解决飞行器通信链路被阻挡,传输信号无法被接收天线接收的问题,通常同时使用2根发射天线发射相同的信号。但是当2根天线的信号同时对地面可见时,2路信号会相互干涉产生自干扰问题,这一现象被称为“双天线”问题[3]。在调制的过程中进行空时编码是解决双天线问题的有效途径之一。CPM信号作为典型的遥测信号,将其与空时码相结合,不仅能够获取较为客观的分集增益和编码增益,还能在近地场景克服信道衰落[4-5]。为了实现空时码与CPM结合的高效益,文献[6]实现正交空时码与全响应/部分响应CPM的联合设计,但是当通信系统的发射天线数大于2时,由于线性编码不满足逐点正交从而无法实现全速率传输,因此文献[7]提出了一种基于L2正交的空时码,并将其推广到了任意发射天线数的通信系统中,在保有正交性的同时,码速率不会降低。
本文在文献[8]的基础上,针对Multi-h CPM与L2正交空时码相结合的通信系统采用最大似然法解调复杂度较高的问题,采用倾斜相位和脉冲截断的算法做简化处理,大大降低了解调的复杂度。内容主要包括:介绍了CPM联合L2正交空时码的通信系统模型,根据2路信号波形的正交性,对最大似然解调算法进行简化设计,并利用常见的波形拟合算法进一步减少逐码块判决时Viterbi算法所需要计算的网格状态数,实现了误码性能与检测复杂度的折衷。
1 L2 STC-CPM通信系统模型
1.1 L2 STC-CPM联合设计
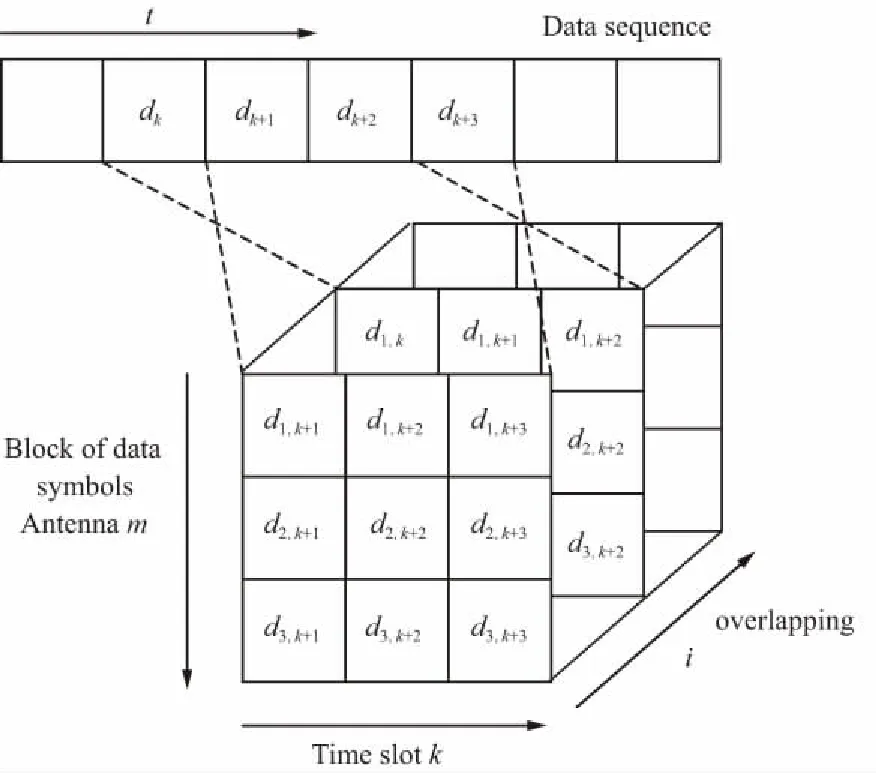
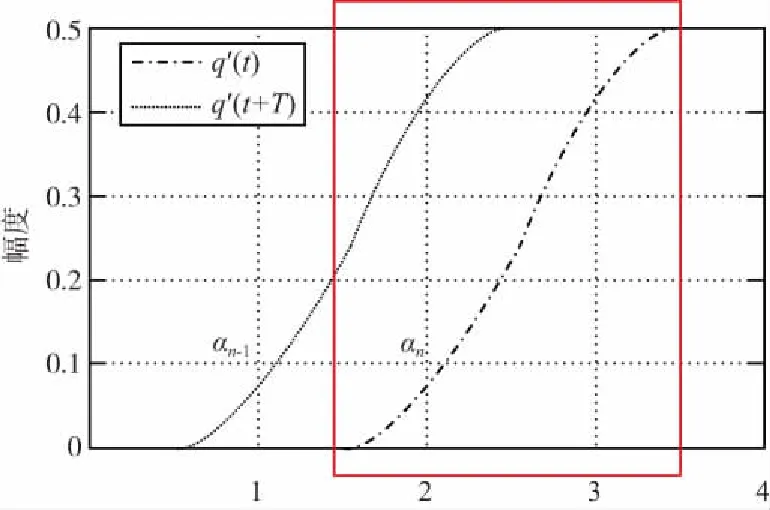
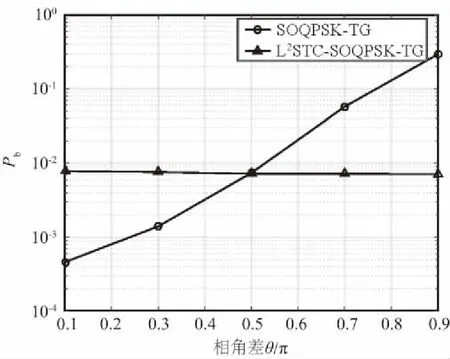
L2空时码的设计不同于传统的正交空时分组码,考虑的不再是构造正交的码字矩阵D,即满足条件:DDH=I,而是构造一种使多路信号的波形满足相互正交关系的空时码。令m=1,…,Lt为天线数,lF=1,…,LF为一个数据流中码块的数目,令k=1,…,LB为一个码块内时隙的个数,若在一个码块间隔内,即当(lF-1)LBT (1) 则称其满足L2正交的条件,不难看出式(11)的意义与L2范数的原理一致: 相比于逐点正交,L2正交对于编码的限制要小,并且逐点正交可以看作是L2正交的一种特殊情况。为了满足波形正交的条件,定义相位修正函数cm,k(t),并令关于天线独立的信息序列为dm=[dm,1,…,dm,Lf],则当前时刻CPM信号的相位表达式为: (2) 图1 L2 STC-CPM通信系统Fig.1 L2 STC-CPM communication system 将L2正交的限制条件分为2个部分:自相关系数必须为1,不同天线的互相关系数必须为0。由于自相关的限制条件是与信号能量相关,若2个天线传输的能量相同即可满足,对于互相关系数的条件则满足: cm′,k(t)]}dt=0。 (3) 由于对于∀m,m′=1,…,Lt且m≠m′式(3)均要成立,即相当于共有Lt2-Lt个子条件,对一个码块时间进行分析,假设: cm,k(t)=cm,k′(t), (4) dm,k=dm′,k。 (5) 即各天线的相位修正函数在码块间满足重复编码的条件,信息序列则满足平行编码的条件。因此,可将互相关条件中关于信息序列的部分项去掉,即可以化简为: (6) 式(6)成立的条件可以分为2个,满足其一即可: (7) (8) 不失一般性,本文考虑的是第2个等式,将式(2)带入式(8)中可得: (9) 式中,Δck,m,m′为: Δck,m,m′=[cm,k(T)-cm,k(0)]-[cm′,k(T)-cm′,k(0)]。 (10) 可以看出,L2正交并不受每个码块的初始相位θm,k影响,根据假设:Δck,m,m′=Δck′,m,m′,将其简化表示为Δcm,m′,则式(9)可化简为: (11) 因此,各天线的修正相位之差只需满足如下形式即可实现L2正交: (12) 式中,i为任意非0整数。可以看出,基于L2正交的编码设计易于推广到任意发射天线的场景,实现较为简便。令cm,r(0)=0,式(12)可以简化为: (13) 式中,cm,r(t)的函数表达式为: (14) (15) 则各发射天线所传输的信号表达式可以表示为: (16) 式中,s(t,d)为传统的CPM信号,故式(15)可作为一种线性的修正函数。对长度为Lg的相位响应函数进行合理加权,可得到另一种修正函数为: (17) CPM信号的相位表达式为: (18) 结合式(2)和式(17),并带入式(18),可得: (19) 观察式(18)和式(19)可知,相对于传统的CPM信号,加上相位修正函数后的CPM信号的符号集可写成: (20) 若采用式(17)这种相位修正函数来实现L2正交只需要在进行CPM调制时改变第m个发射天线的符号集,进行相应的符号映射即可。实现L2正交的过程中信息序列与空时码块的对应关系如图2所示(以Lt=3,LB=3为例),图2中显示每3个信息比特可映射为一个大小为3×3的码块组,由于采用平行编码,即满足dk=d1,k=d2,k=d3,k。 图2 信息符号与空时码块对应关系示意Fig.2 Schematic diagram of the correspondence between information symbols and space-time code blocks 对于CPM这类记忆性信号,通常采用Viterbi译码算法来实现最大似然序列检测[9],但关联长度较长且相位状态数较多的Multi-h CPM信号检测复杂度较高,在工程中实现高速传输非常困难[10-11],经常使用简化算法—倾斜相位与脉冲截断联用是较为有效的算法[12]。同时,可利用L2正交分组空时码各路信号的波形之间的正交性,来减少检测的复杂度。 每个码块的最大似然度量可以表示为: (21) (22) 考虑到引入修正函数后各路信号波形的正交性: (23) 因此,式(22)中的交叉项可以去掉,可重新表示为: (24) 由于式(24)中的2|r(t,d)|2表示的是信号的能量,与码块信息序列无关,可以忽略,令2P为相位状态数,那么每个码块的解码复杂度为2LtPMLB+Lg-1。可以看出其复杂度会随着发射天线数的增加而线性提高。同时,采用平行编码的方法也大大降低了检测的复杂度,其最大似然度量可表示为: (25) 对应的在接收端,可以定义一个修改的接收信号,表示为: (26) 则最大似然度量可表示为: (27) 算法中,CPM信号的相位表达式中的符号αi可以用Ui=(αi+M-1)/2来代替,则CPM的相位可表示为: (28) 式中,W(t)是与符号不相关的项, (29) 将式(28)中第2个等式的第1项,即累计相位项取2π的模,可得: (30) Vn=[Kn-LUn-L+Vn-1]modP。 (31) 因此,累计相位取值的集合由{0,1,2,…,2P-1}变为了{0,1,2,…,P-1},即累计相位的状态数减少到了原来的一半[13]。将此时所有与CPM网格状态图相关的量定义为状态转移的向量: σn={Vn,Un-1,Un-2,…,Un-L+1}, (32) 图3 脉冲截断算法原理Fig.3 Pulse truncation algorithm schematic 观察图中方框圈出的区域可知,对[1.5T,2.5T]时间段波形产生影响的符号αi从3个减少到了2个,所涉及到的比特数目减少相应的检测复杂度也会降低,将新的相位响应函数q′(t)带入式(28)可得: (33) 式中,W′(t)可表示为: (34) 同样的,累计相位变为: (35) 将采用TP+FPT的简化算法的复杂度与简化前的MLSD算法复杂度进行对比,相关参数如表1所示。 表1 TP+FPT简化算法与MLSD算法的复杂度对比 Tab.1Comparison of complexity between TP+FPTsimplified algorithm and MLSD algorithm 算法相位状态数网格状态数MLSD2P2LtPMLB+Lg-1TP+FPTPLtPMLB+L′g-1 同样以ARTM CPM信号为例,采用TP+FPT简化算法后,其相位状态数降为16。当LB=2时,两发一收的L2STC-CPM遥测系统中,Viterbi检测时的网格状态数降为2 048个,相比于具有16 384个网格状态的MLSD算法,大大降低了检测复杂度。 在两发一收的L2STC-CPM遥测系统中,发射器与接收天线间的距离通常远大于2根发射天线间的距离,因此可假设2个子信道信道响应g0和g1的幅值a0=a1=1,当2根发射天线对接收天线均可见时,其信道响应的相角差θ会影响信号检测的性能,令g0,g1分别表示为g0=1,g1=exp(iθ)。 仿真采用的CPM调制方式为单指数CPM中的SOQPSK-TG,本文假设2路信号没有时延且2个发射天线的功率相等,相干解调部分都假设对信道参数有完美的估计。令当前信噪比为5 dB,θ=0.1π,采样点数为16,信道为高斯白噪声信道,图4为使用本文设计空时编码与不使用空时编码的参考系统的误码率仿真曲线。 图4 L2STC-CPM遥测系统与CPM遥测系统的误比特率随信道响应的相位差变化关系Fig.4 Variation of the bit error rate of the L2STC-CPM telemetry system and the CPM telemetry system with the phase difference of the channel response 可知随信道响应的相位差的增大,无空时编码的系统误码性能迅速衰减,而采用L2空时码的遥测系统的误码性能基本不受影响。因此设计的L2STC-CPM遥测系统可有效地解决“双天线问题”。 图5为在AWGN信道下,采用TP+FPT的(Multi-h CPM为ARTM CPM信号)遥测系统和未采用简化算法的L2STC-Multi-h CPM遥测系统的误码曲线。由图5可以看出,在低信噪比情况下,采用TP+FPT简化算法对误码性能影响较小。 图5 L2STC-Multi-h CPM遥测系统基于TP+FPT的最大似然检测与不采用简化算法的误比特率随信噪比变化关系Fig.5 Variation of the bit error rate of the maximum likelihood detection algorithm based on TP+FPT and the method without simplification algorithm of the L2STC-Multi-h CPM telemetry system with the signal-to-noise ratio 为了解决多天线遥测系统中2路发射信号同时对接收端可见时相互干涉而产生的“双天线问题”,提出了一种基于正交设计的L2STC-CPM遥测系统模型。在L2STC-CPM遥测系统模型中,引入相位修正函数使得各路信号的波形相互正交,并且针对L2STC-Multi-h CPM遥测系统的解调复杂度过高的问题,提出采用TP+FPT的简化检测算法,大大降低了联合检测的复杂度。仿真结果证明,该检测算法的误码性能损失较小,即遥测系统具有高可靠性。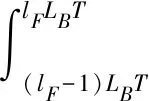
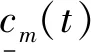
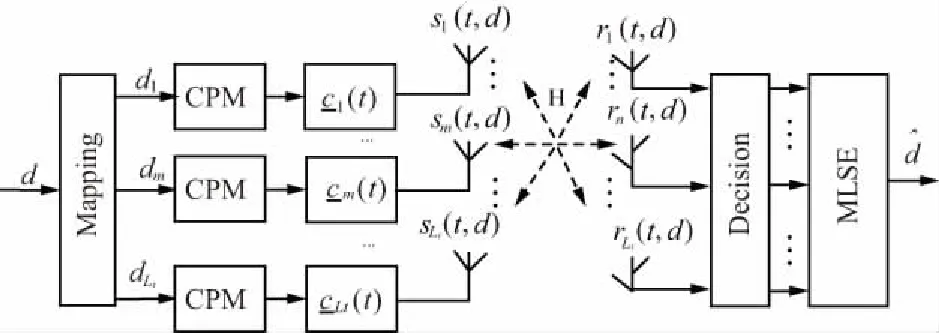
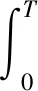

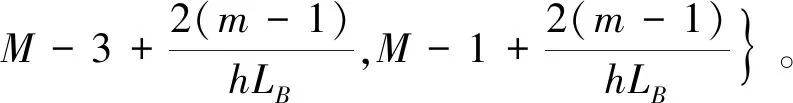
1.2 基于TP+FPT的最大似然检测算法
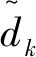
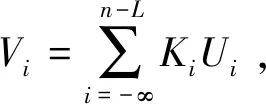
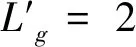

2 仿真结果分析

3 结束语
