基于改进烟花算法的ELM 分类模型*

刘 唐，周创明，周 炜，王晓丹

（1.解放军31436 部队，沈阳 110000；2.空军工程大学防空反导学院，西安 710051；3.西安财经大学行知学院，西安 710038）

0 引言

人工神经网络因其具有很强的记忆力和鲁棒性而被众多领域广泛应用。极限学习机［1］是一种快速学习的单隐层前馈神经网络，隐层输入权值和偏置根据输入节点和隐层节点数随机生成，根据隐层输入权值和偏置求得隐层输出矩阵。尽管极限学习机与标准的神经网络相比有很多的优点，但是并不能满足人们对精度更高和速度更快的需要，因此，很多优化的ELM 算法出现。例如小波核极限学习机、粒子群极限学习机、蚁群优化极限学习机、人工蜂群算法优化极限学习机等［2］，优化了极限学习机的分类性能或极限学习机的隐层节点。

受烟花在空中爆炸产生火花，照亮临近的天空并构造出美丽的图案这一现象的启发，谭营［3］等在首届国际群体智能大会上提出了烟花算法。烟花算法是一种由爆炸产生火花的群体优化算法，它具有局部探索能力和全局搜索能力，是一种求解复杂问题最优解的高效方法。因此，烟花算法在许多领域都有应用［4-5］。

极限学习机的隐层输入权值和偏置随机生成可能使误报率较大，并导致使用许多无效隐层节点。因此，为了得到更高的精度和更好的泛化性能，提出了基于改进的烟花算法的ELM 分类模型，并通过实验验证，结果表明：改进烟花算法极限学习机（IFWAELM）具有更高的精度、更好的泛化性能，同时所需的隐层节点数更少。

1 极限学习机

以上N 个方程的矩阵形式可写为

式中：

H 为隐层输出矩阵，H 的第i 行表示全部隐层节点与输入xi相关的输出。

ELM 算法对输入权值wi和偏置bi的值采取随机设置，在输入样本集（xj，y）j，j=1，2，…，N 给定的情况下，隐层输出矩阵H 也被确定了，Y 从而求得符合以下条件的学习参数：

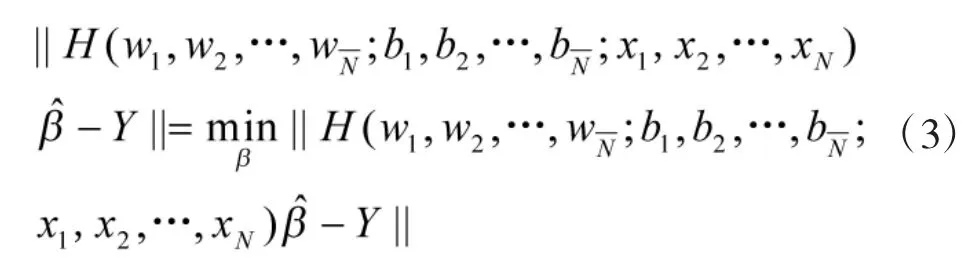
由上式得到的解为最小范数二乘解：

式中：H+为H 的Moore-Penrose 广义逆。

2 烟花算法

烟花算法是一种模拟烟花爆炸过程的新型群体智能优化算法，与一般的群智能算法类似，对于一个优化问题，经过多次迭代搜索求得最优解，具体描述过程参考文献［4］。烟花算法主要有爆炸算子、变异算子、映射规则和选择策略4 部分组成，爆炸算子主要由爆炸半径、爆炸火花数、爆炸强度等组成；变异算子一般选择高斯变异［8-9］，选择策略有随机选择和基于距离选择等。

烟花算法具有局部探索能力和全局搜索能力自动调节功能，其中单个烟花的爆炸火花数和爆炸半径是不同的，适应度值低的烟花爆炸半径小，在其周围具有更大的挖掘能力；适应度值高的烟花爆炸半径大，在全局范围具有更大的搜索能力［10］。初始化每个烟花的爆炸半径Ri和爆炸火花数Si的公式分别为：

为了避免适应度值高的烟花爆炸产生过少的火花，同时限制适应度值低的不会产生太多的火花［3］，对每个烟花产生火花数进行如下限制：

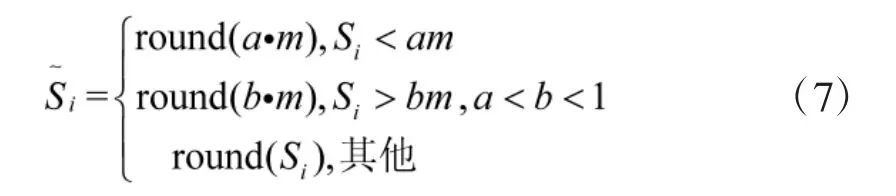
式中：a、b 是两个给定常数，round（·）是取整函数。

3 改进烟花算法的ELM 分类模型

针对极限学习机随机生成的隐层输入权值和偏置可能只有很少部分是较优的，更多的是较差的，更可能造成误报率过大，导致使用更多无效隐层节点。本文提出了改进烟花算法极限学习机。改进烟花算法（IFWA）是一种新型群体智能优化算法，在提高精度的同时有很强收敛性、鲁棒性和稳定性。IFWA 通过多次迭代搜索求解出最优的隐层输入权值和偏置，然后训练极限学习机得到分类模型。

3.1 算法改进

3.1.1 自适应动态爆炸半径

在动态搜索烟花算法中烟花种群被分为核心烟花（core fireworks）和非核心烟花（non-core fireworks），核心烟花就是目前烟花种群中适应度值最低的烟花。非核心烟花的爆炸半径用式（5）计算，核心烟花xc的爆炸半径用Rc表示，计算如下：

式中：Ca、Cr是两个调整变量，分别用来增加和减小爆炸半径；t 为当前迭代次数为新的最优火花个体。

针对动态搜索烟花算法面对多峰问题时可能陷入局部最优，导致算法提前收敛的问题，提出在算法中增加一个产生火花的自调节算子。自调节算子利用搜索过程中的历史成功信息和最优的烟花位置来学习总结。具体如下：

式中：xbest为目前最优烟花位置；z 是记忆因子，用于调节新生火花与目前最优烟花间距，其使烟花向种群中最好烟花个体学习并向历史最优烟花位置逼近，其产生如下：

式中：randz（a，b）是位置、尺度参数分别为a、b 的柯西分布；rand 为服从均匀分布的随机数［11］。p 是变量，计算如下：

式中：t1、t2分别为大参数、小参数时，柯西分布产生c 的次数；p 初始值取0.6，每迭代T 次更新一次，即对这次迭代过程进行学习总结。由于记忆因子是向历史最优烟花学习生成的，为后面的求解提供了更优的候选解和更佳的寻优方向，增强了算法全局的鲁棒性和稳定性。

3.1.2 变异算子生成策略

在FWA 中高斯变异算子采用随机选取原则，这使得生成更优烟花的几率降低。为提高生成更优烟花的几率并且让变异具有更好的方向性，选择目前种群最优烟花作为变异对象，变异公式如下：式中：xk是变异烟花个体的第k 个分量；x（best，k）是目前种群最优烟花的第k 个分量；g～N（0，1），q 是高斯变异概率，反映种群中最优烟花对变异后火花产生的作用大小。作用越小，其值越大。作用越大，其值越小［5］。具体取值根据实验具体情况而定。

3.1.3 映射规则

产生的一些火花可能超出边界，为解决这一情况，提出如下映射规则来处理超出边界的火花：

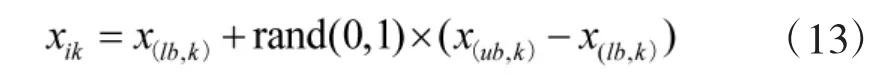
式中：xik为第i 个烟花的第k 维分量位置；x（lb，k）、x（ub，k）分别表示烟花第k 维分量位置的下界和上界。

3.1.4 精英选择策略

在FWA 中采用的是基于距离的选择策略，增加选择多样性的同时也增加了算法的迭代时间。为加快选择速度，采用精英选择策略，在候选集K（烟花种群、爆炸火花）中按下式概率选择：

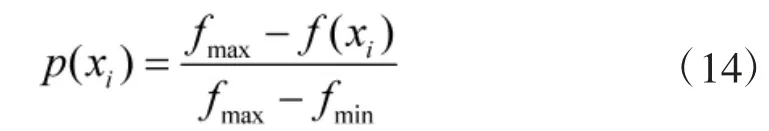
易知，适应度值越低的个体，被选中的概率越大，反之则概率越小。特别地，适应度值最低（即目前最优）的个体被选中的概率为1，如果按此方法选出的数不够N 个，则在候选集中采用轮盘赌方法选取足够个填补。

3.2 算法描述

利用原始ELM 求出隐层输出权值（选用效果较好的Sigmoid 作为激励函数），并以训练样本集求得的均方根误差（RMSE）为IFWA 的适应度值函数。算法的维度大小取n=h（d+1），h 是输入神经元个数，d 是隐层节点数［12］。算法中参数设为r=36，m=56，a=0.05，b=0.7。IFWAELM 算法流程如图1：

图1 IFWAELM 算法流程图

IFWAELM 算法具体过程如下：

1）初始化随机生成N 个烟花，设定初始迭代次数i=1；

2）根据适应度值函数计算每一个烟花的适应度值；

3）使用式（5）计算非核心烟花的爆炸半径，使用式（8）～式（11）计算核心烟花的爆炸半径；

4）使用式（6）和式（7）计算每个烟花产生的爆炸火花数Si；

5）选择目前种群最优烟花使用式（12）进行高斯变异操作，并选出最优火花，使用式（13）把超出边界的火花映射到可行域内；

6）计算所有火花的适应度值（包括爆炸火花和变异火花）；

7）使用式（14）从候选集K 中最合适的N 个个体作为下一代烟花；

8）令i=i+1，判断是否达到结束条件，如果没达到则返回2）继续进行。

根据上面算法求得最优的烟花个体，即最优的隐层输入权值和偏置，代入得到输出权值矩阵，根据ELM 的式（3）和式（4）求得符合条件的学习训练参数。

4 实验与结果分析

本实验采取的数据为美国国防部高级研究规划署（DARPA）在1999 年KDD 竞赛所供给的入侵检测系统评估的数据［13］。数据集含有一个标明入侵攻击类型的标识属性，一共有23 种类型，Normal 为正常的网络活动，其他22 种（Smurf、Back、Neptune等）为入侵行为［14］。将其映射为5 大类型，即Normal、DoS、R2L、U2R 和Probing。实验数据需要进行数据预处理和数据划分。

所采用的学习训练数据集（Kddcup10per）共有494 021 条记录，其中标记为Normal 的有97 278 条记录，占19.6%，而攻击记录396 743 条，占80.4%。测试数据集共有311 029 条记录。

此数据集中有41 个特征属性，其中34 个特征属性为数值型变量、4 个为二元变量、3 个为标称变量（属性及其意义见文献［13］）。在实验检测过程中发现，并不是所有的特征属性都对入侵检测有帮助，有些特征属性甚至会降低辨别率。根据文献［15］，属性约简后如表1：

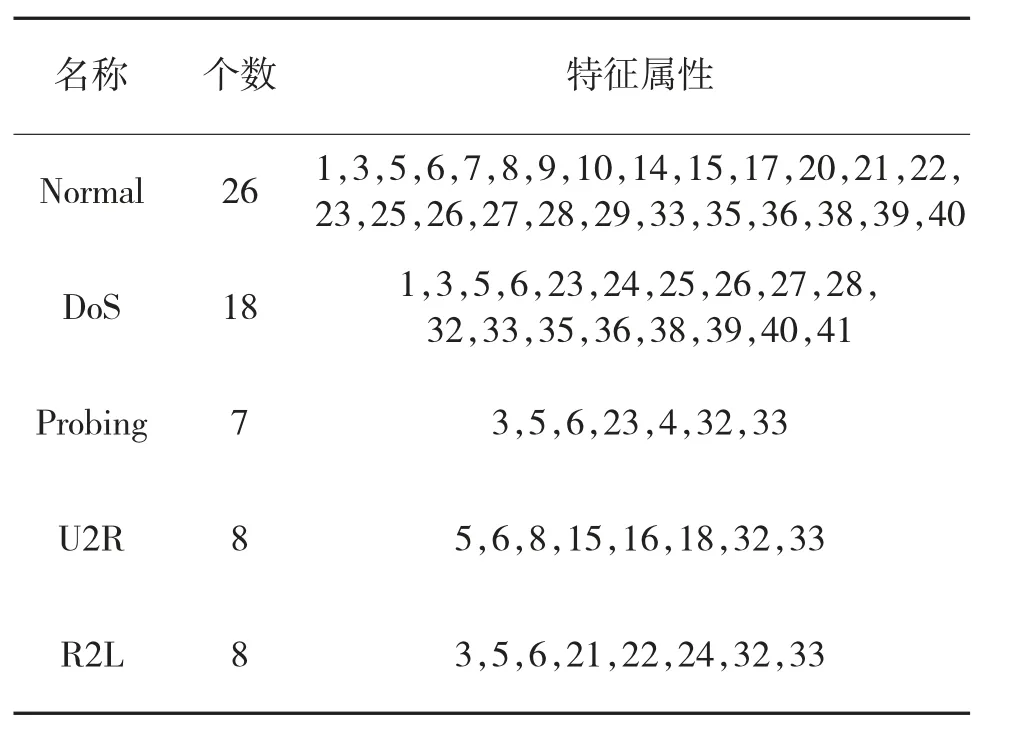
表1 特征属性约简

此外，原始数据中有34 个数值属性，但每个属性的取值范围却大不相同，所以，对数据进行规范化处理，将其规范化到区间［-1，+1］。采用如下公式：

规范化后，upper 为上界，取+1；lower 为下界，取-1；max（fi），min（fi）分别表示属性fi的最大值和最小值。

数据划分即把原始数据分成学习训练样本集和测试样本集。学习训练样本集是从原始学习训练数据集随机抽取出来的10 000 条数据；测试样本集是从原始测试样本集中随机抽取出来的10 000 条数据，包括Normal 数据5 182 条、DoS 攻击3 869条、R2L 攻击276 条、U2R 攻击71 条、Probing 攻击602 条［16］。

4.1 隐层节点数分析

理论上，随着迭代次数增加到一定后，误报率降低程度变得十分微小，学习训练时间却依旧增大。因此，迭代次数不宜取太大。设IFWAELM 的迭代次数为30，对实验结果去掉一个最低和一个最高后取平均值（下同）。分析隐层节点数对原始ELM、FWAELM 和IFWAELM 的影响，结果如图2。

图2 隐层节点数的影响对比

由图2 易知，在相同的迭代次数时，IFWAELM比原始ELM 和FWAELM 都先收敛到最小值，并且IFWAELM 在测试误报率到最小值时的隐层节点数为8，而ELM 和FWAELM 的测试误报率到最小值时隐层节点数分别为18 和10。易得在测试误报率取最小值时，IFWAELM 比原始ELM 和FWAELM分别少用10 个和2 个隐层节点。更有IFWAELM 比原始ELM 和FWAELM 能达到的最小测试误报率分别降低了72.22%和61.21%，在隐层节点数逐渐增长到60 的过程中，ELM 的测试误报率先减小后趋于稳定。IFWAELM 和FWAELM 分别在隐层节点数为8 和10 时，收敛到最小值后，直到60 的过程中基本保持稳定状态。

4.2 迭代次数分析

设IFWAELM 的隐层节点数为8，迭代次数为i=1，4，…，40。分析迭代次数对IFWAELM 的影响，结果如图3。由图易知，IFWAELM 的训练误报率和测试误报率都随着迭代次数的增加而减少，最后趋于平稳状态。此外，由于迭代次数的增加会使学习训练时间增加，所以考虑测试误报率降低程度十分微小的情况，设IFWAELM 的最佳迭代次数为21。综上所述，IFWAELM 的隐层节点数取8，迭代次数取21。

4.3 算法性能分析

在对隐层节点数和迭代次数分析的基础上，我们还将IFWAELM 和FWAELM、ELM、BP 及SVM 的性能作了对比。设IFWAELM 的隐层节点数为8，迭代次数为21。设FWAELM 的隐层节点数为10，迭代次数为23。设ELM 的隐层节点数为100，重复运行100 次后，取平均值。激励函数选用效果较好的Sigmoid 函数。BP 采用matlab 自带的工具箱函数来学习训练，SVM 的参数采用交叉验证来完成［17-19］，实验结果如表2：

图3 迭代次数对IFWAELM 误报率的影响

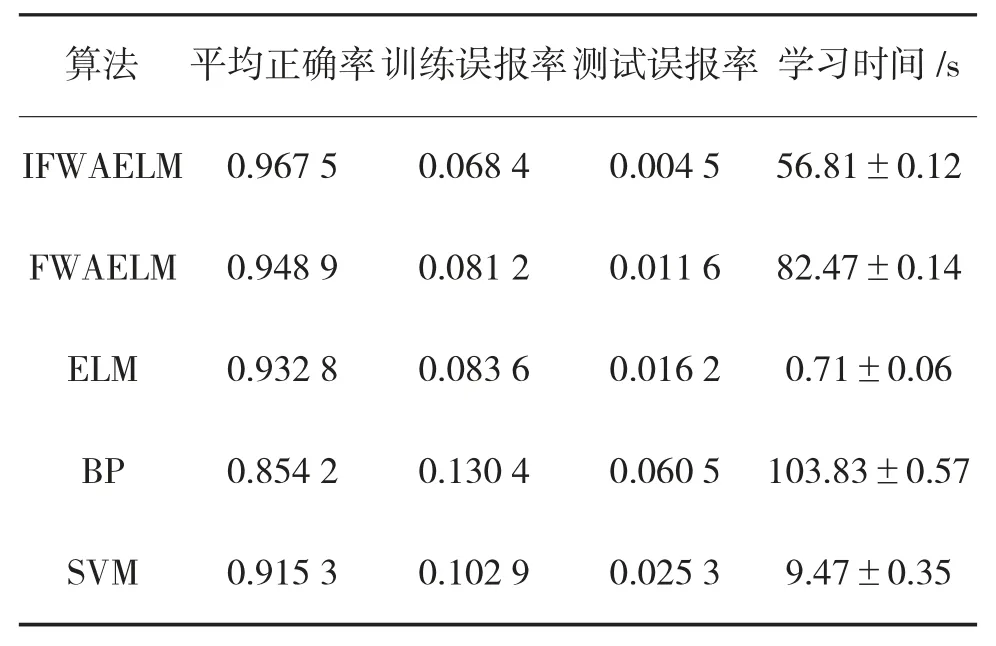
表2 算法性能对比

从表2 可以看出，IFWAELM 算法的测试平均正确率相比BP 算法高出11.33%，比其他算法也都高出几个百分点。训练误报率和测试误报率也是5种算法中最低的，测试误报率相比其他算法更是低一个数量级。在这5 种算法性能对比中，IFWAELM性能最好。IFWAELM 只用8 个隐层节点就超越了ELM 用100 个隐层节点的测试平均正确率，并且达到更低的训练误报率和测试误报率。相对于FWAELM，IFWAELM 也在使用更少的隐层节点和迭代次数情况下，取得了更好的效果。与BP 和SVM相比，测试平均正确率和误报率更是优势明显。

5 结论

本文在ELM 的基础上提出了改进烟花算法优化极限学习机的分类模型。该方法利用改进烟花算法优化极限学习机的隐层输入权值和偏置，综合了改进烟花算法和极限学习机的优点。通过实验验证表明：IFWAELM 达到最小测试误报率比原始ELM和FWAELM 所用隐层节点数更少，并且IFWAELM比原始ELM 和FWAELM 能达到更小的测试误报率。迭代次数和学习训练时间成正比。最后5 种同类算法的性能对比，IFWAELM 在测试平均正确率和误报率等方面都是最优的。虽然IFWAELM 比FWAELM 的学习训练时间有所减少，但是与原始ELM 相比，IFWAELM 的学习训练时间还是很长，这是下一步需要研究的方向。