基于Volterra 级数的航空年事故率预测方法*
2020-04-02郭之俊董泽磊
王 瑛,郭之俊,孙 贇,李 超,董泽磊
(1.空军工程大学装备管理与无人机工程学院,西安 710051;2.解放军95084 部队,广东 佛山 528000)
0 引言
航空年事故率是包括人、机、环在内的复杂系统在构成系统的组件失效、组件间复杂耦合关系、系统外部干扰,以及导致系统危险状态的单个组件行为共同作用下涌现出来的损失事件。事故是系统组件在微观层面发生非线性耦合作用下而表现在宏观层面的涌现行为[1]。对于航空年事故率的预防既要在微观层面针对构成装备系统的部件进行可靠性分析、人为因素分析、环境分析等系统组元分析,也要在宏观层面对航空装备的安全态势进行预测与评估,特别是对于航空年事故率的数目进行准确预测[2],通过量化的指标反映航空装备的安全状况,根据预测结果确定系统的危险,建立装备系统目标,设计安全约束,从系统的角度出发实现装备的安全涌现特性。因此,航空年事故率的准确预测对实现航空安全,充分发挥武器装备的性能具有重要的现实意义[3]。
美国开展航空年事故率的预测工作始于20 世纪70 年代[4-5],目前已经构建出比较完整的年事故率预测体系,该体系在安全态势研究、年事故率预防[5]等方面发挥了积极的作用[6-7]。
国内针对航空年事故率的预测工作从1987 年开始,应用的方法比较单一,预测精度难以满足装备管理需求。国内的预测主要以灰色模型及其组合模型为主,但是这些方法只能从某种程度上反映事故致因的复杂性,不能完全反映出事故致因非线性耦合的特点,因此,预测效果都不理想,特别是当系统无法提供其发展变化的最新信息时,模型的预测效果会骤然降低。
航空年事故率的产生是“人-机-环”等多种危险因素耦合交互决定的一种整体涌现结果,事故的预测表现出较强的非线性特性,根据相邻数据存在相关性的特性[8],对历年航空年事故率数据进行处理发现,航空装备相邻年份的事故万时率差值表现出一定的混沌特性。混沌具有随机性同时符合确定的运动规律,其复杂性可以更好地描述事故致因因素的复杂性,本文尝试建立混沌预测模型[9],对航空年事故率进行预测。
本文首先对原有年份的事故率数据预处理,得到相邻年份事故率的差值,然后通过0-1 混沌特性判定方法确定该时序的混沌特性。针对处理后的时序,利用相空间重构的方法重构相空间,通过互信息法确定延迟时间[10-11],通过假近邻法确定嵌入维数,重构的相空间在几何意义上等价于航空年事故率非线性动力学系统[12-13]。在上述重构的相空间的基础上,通过利用改进的Volterra 级数预测的方法对时间序列进行预测[14]。
1 航空年事故率时序混沌特性判定
0-1 混沌特性判定方法是由Melbourne 与Gottwald 于2009 年提出[15],该方法最大的特点是不需要重构相空间,可以直接对其进行混沌特性的判定。首先,定义两个平移变量p(n)与q(n)[15]。
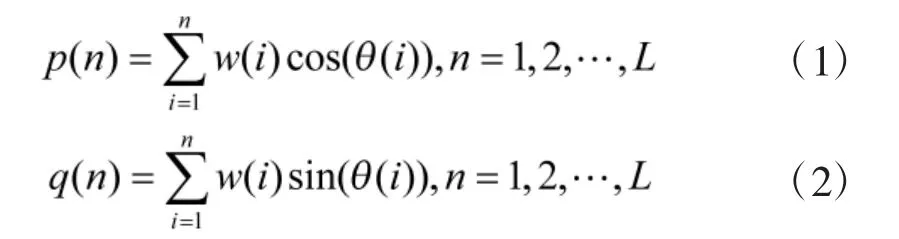
如果p(n)与q(n)的相图为无规则运动,那么原时间序列中存在混沌现象,反之,不存在。为了研究p(n)与q(n)的散布特征,定义均方位移M(n)。p(n)与q(n)的相图为无规则运动时,M(n)关于时间线性递增,其渐进增长率Kc→1,如果Kc→0,则原时间序列不存在混沌特性[15]。
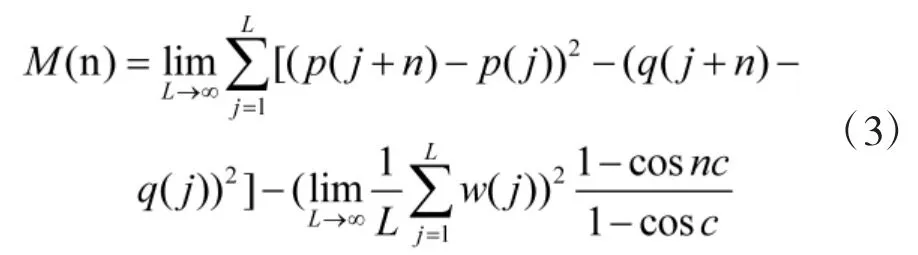
考虑到事故数据不易收集,本文以美军1971年-2001 年A 级飞行事故10 万时率为例对混沌预测的可行性进行讨论,相邻年份事故万时率的差值如表1 所示。该差值组成的时间序列共30 组数据,数据具有混沌性,为了进一步研究,同时弥补航空年事故率数据较少的不足,本文基于二次插值法在每组数据间插入9 组数据,则原始数据扩充为291组数据,如图1 所示,扩充后数据集第10i+1 组数据为原数据集第i 组数据的原始值(i=0,1,…,29),利用0-1 混沌特性检验扩充数据的混沌特性,保证数据的一致性。
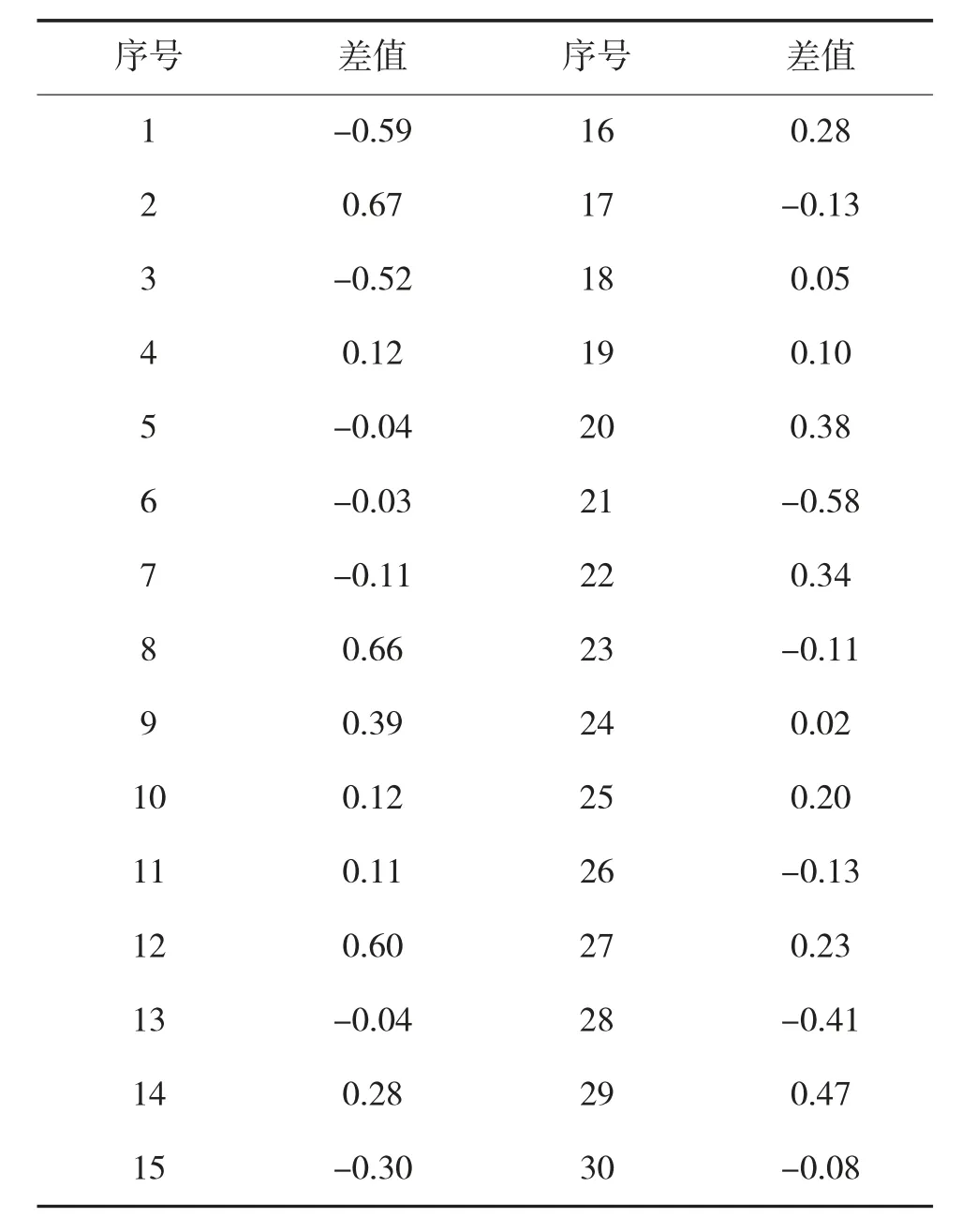
表1 相邻年份事故率差值(%)

图1 相邻年份事故率差值时序图
利用0-1 混沌特性判定方法对相邻年份事故万时率差值时间序列进行分析,可以得到p(n)与q(n)的相图,如图2 所示,作出M(n)随时间的变化图,如图3 所示。分析图2 和图3 可得,p(n)与q(n)的散布特征符合布朗运动,M(n)随时间线性增长,渐进增长率Kc=0.998 6,即Kc→1,所以航空装备相邻年份事故率的差值时序具有混沌特性。

图2 p(n)与q(n)的相图

图3 均方位移的变化图
2 航空年事故率时序的相空间重构
通过上节的分析可以判定该时间序列具有混沌特性,在本节中对该时间序列进行相空间的重构。
2.1 相空间的重构
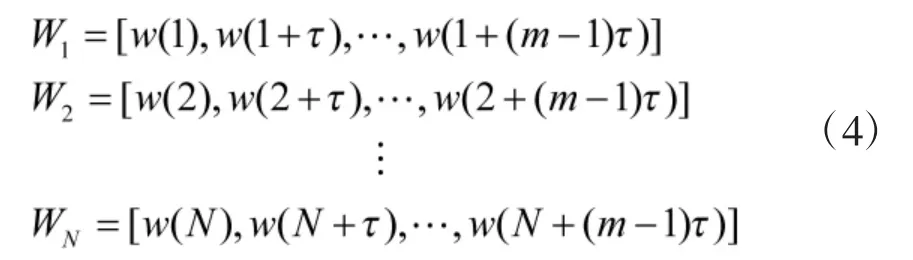
由此重构系统的动力学模型F(·)为:

式中,T 表示的是预测步长。
在相空间的重构过程中,延迟时间和嵌入维数的确定非常重要,对于相关参数的选取有很多研究,下面求解相应的参数。
2.2 延迟时间和嵌入维数的确定
互信息法[9]将互信息函数的第1 个极小值点对应的时延确定为延迟时间。
通过互信息法确定相邻年份事故万时率差值时间序列的平均互信息与延迟时间的关系图如图4所示,分析图4 可知,该时间序列在时取得第1个极小值,即相空间重构的延迟时间为。
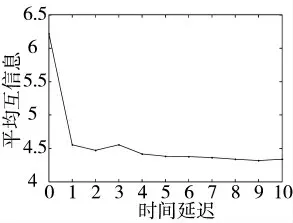
图4 平均互信息与延迟时间的关系
假近邻法[10]要求当相空间的嵌入维数增大至某个数值时,相空间中的轨道会充分展开,假近邻点消失,此时的嵌入维数即为最佳嵌入维数。
通过假近邻法确定相邻年份事故万时率差值时间序列的嵌入维数与假近邻率的关系图如图5所示,分析图5 可知,该时间序列从m=6 时假近邻率趋于恒定,即相空间重构的嵌入维数为m=6。

图5 假近临率与嵌入维数的关系
2.3 最大Lyapunov 指数
通过wolf 方法,在重构的相空间基础上进行计算可得Lyapunov 指数,Lyapuvov 指数的示意图如图6 所示,大部分指数,比较可得最大Lyapunov 指数为,即该时间序列具有混沌特性,由此验证了上文中0-1 混沌特性判定方法的正确性。

图6 Lyapunov 指数示意图
3 Volterra 自适应预测模型
根据上节的计算可知,重构相空间可以得到混沌系统的动力学模型F(·),本节通过Volterra 级数展开式对混沌系统动力学模型F(·)进行逼近,由此构造出混沌时间序列的Volterra 自适应预测模型。假设该模型的输入为

输出为

Volterra 级数展开式的计算如式(5)所示。
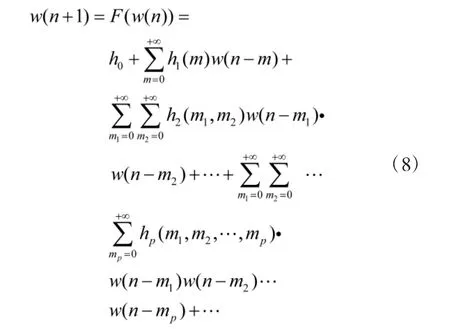

上式可化简为

上式中

定义预测的误差为:

可以应用归一化LMS(NLMS)的自适应算法实时调整滤波器的系数[16-21]。相关研究表明,权值的调整量大小往往由输入向量U(n)和U(n-1)的相关系数ρ(n)决定,当输入向量U(n)同U(n-1)正交,即相关系数ρ(n)=0 时,该滤波器的收敛速度最快。为表示输入向量U(n)在当前的时刻同前一时刻不相关的部分可以引入如下新的向量:
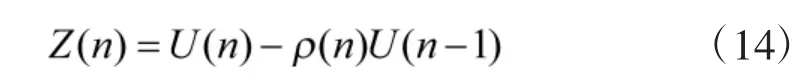
因为
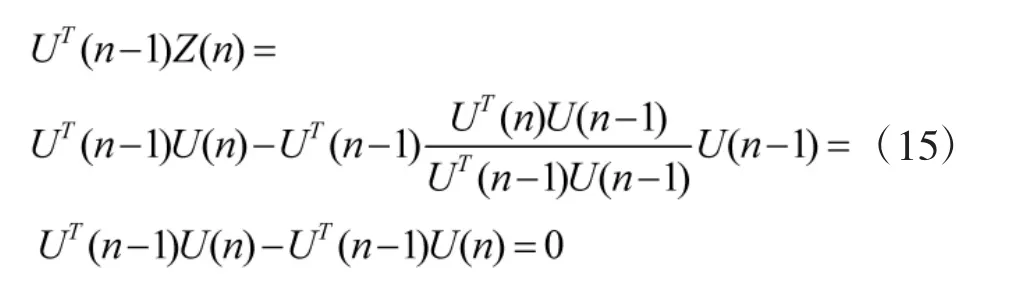
所以,Z(n)与n-1 时刻的输入U(n-1)是正交的,所以可以用Z(n)作为输入向量,滤波器的系数可以按照如下方式进行更新:
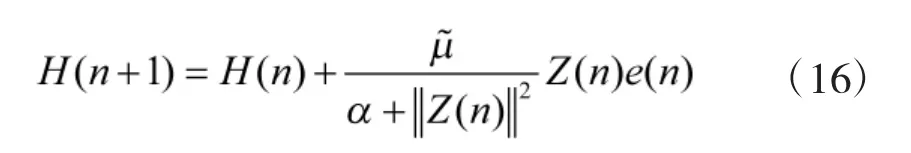

图7 相邻年份事故率差值时序预测流程图
4 实验分析
将插值扩充后的291 组航空装备相邻年份事故率差值的时间序列数据分为两组,前251 组数据(即原始数据集前26 组数据)为训练集,后40 组数据(即原始数据集后4 组数据)为测试集。
将数据输入Volterra 自适应预测模型,对时间序列数据进行预测,可得到预测数据与真实数据的对比图,如图8 所示,两者的预测误差如图9 所示,其中预测集中第10、20、30、40 个数据分别对应1998 年-2001 年的预测差值,根据1997 年数据可以计算得到1998 年-2001 年的事故率。

图8 真实值与预测值

图9 预测误差
通过图8、图9 可以看出,Volterra 自适应预测模型预测效果较好,精度较高,将该预测结果与灰色时序组合预测模型进行比较,如表2 所示。从表中可见,Volterra 自适应预测模型的预测相对误差控制在2%以内,虽然相对误差有逐渐变大的趋势,但预测精度仍然比较高,满足航空年事故率的预测要求。

表2 混沌时序模型的1998 年~2001 年预测结果
5 结论
研究证明:经过0-1 混沌特性判定方法判定美国空军1971 年-2001 年航空装备相邻年份事故率差值时间序列具有混沌特性,并通过最大Lyapunov指数的方法验证其有效性。
二阶Volterra 自适应预测模型既利用系统的线性因素,又利用系统的非线性因素,更符合混沌系统的特性,能够很好地反映相邻年份事故率差值时间序列的变化规律。
本文采用混沌时间序列的预测方法对航空年事故率进行预测的尝试是有效的,经过与灰色时序组合预测方法对比,本文方法精度更高,为航空年事故率的预测研究进行了新的尝试。
