考虑背景风险的多期破产控制投资组合模型

李莹莹， 刘勇军

（华南理工大学工商管理学院，广州 510640）

Markowitz［1］提出均值-方差投资组合模型，该模型奠定了现代金融学理论的基础. 均值-方差投资组合模型分别以资产收益的均值和方差作为收益和风险的度量. 然而，投资者在投资过程中不仅会面临投资风险——由被选择金融资产的不确定收益产生的风险，还会面临背景风险——在金融市场中无法交易或不交易的风险. Tsetlin和Winkler［2］指出，因金融市场不完善而无法进行对冲或无法完全对冲的风险，及投资者在考虑风险管理成本后不进行风险管理的风险，均视为背景风险. 现有研究将背景风险分为加性背景风险和乘性背景风险. Jokung［3］指出，加性背景风险是附加于财富的，乘性背景风险是部分或完全作用于财富的.Tsetlin和Winkler［2］列举两类背景风险的例子，其中加性背景风险包括人力资本、劳动收入、专有收入、投资收益等，乘性背景风险包括汇率、税率、通货膨胀等. 在现实中，当投资者同时面临投资风险和两类背景风险时，投资者在投资决策过程中应不只考虑投资风险对投资决策的影响，还应关注两类背景风险对投资决策的影响. 因此，研究考虑两类背景风险的投资决策问题是十分必要的.

在现实中，投资者会根据市场环境变化来调整投资策略，因此许多学者将单期投资情形推广到多期投资情形. Sun等［4］提出漂移粒子群优化算法，并将其应用于多期组合问题. Sadjadi等［5］研究模糊环境下考虑不同借贷利率的多期投资组合优化问题，并通过漂移粒子群优化算法进行求解. Najafi和Mushakhian［6］研究考虑期望、半方差和指定置信水平下的条件风险值的多期投资组合模型，并设计遗传算法和粒子群算法的混合算法对模型进行求解. Babazadeh和Esfahanipour［7］研究考虑实际约束和交易成本的多期均值-VaR投资组合优化模型，并设计新的非支配排序遗传算法对模型进行求解. 姚海祥等［8］研究任意多种风险资产存在一般收益序列相关的多期投资组合均值-方差模型. 张鹏等［9］研究具有最小交易量限制的多期均值-半方差投资组合优化模型，并通过前向动态规划方法对模型进行求解. 然而，在多期投资过程中，投资者不仅关注终端财富，还关心中间过程的财富状态，因此一些学者在多期投资问题中考虑破产控制. 如Zhu等［10］研究考虑破产控制的广义均值-方差多期投资组合模型. Wei和Ye［11］研究随机市场下考虑破产约束的多期均值-方差投资组合选择模型. Yu等［12］研究考虑破产控制的多期均值-绝对偏差投资组合模型. Li等［13］研究不确定环境下考虑交易成本和破产控制的多期投资组合均值-方差模型.

虽然上述投资组合优化模型考虑了投资中间过程的财富状态，对多期投资进行破产控制，但是没有考虑对投资者财富有影响的两类背景风险. 许多研究指出，背景风险对投资决策产生影响，投资者应关注总风险而不仅仅是投资风险. Pratt［14］指出，在一般效用函数下，不公平加性背景风险的增加会降低对风险资产的分配. Gollier和Pratt［15］提出“风险脆弱性”概念，指出不公平的加性背景风险会使投资者的行为更加谨慎，并推导出风险脆弱性的充分必要条件. Eeckhoudt 等［16］发现随着背景风险的增加，投资者表现得更加风险规避. Li等［17］研究可能性投资组合模型中背景风险对投资的影响，指出收益相同的情况下，存在背景风险将使方差更高. Huang和Di［18］，Zhai和Bai［19］发现，当其他条件相同时，具有背景风险的最优预期收益小于没有背景风险的收益. 何兴强等［20］应用Probit回归分析探讨劳动收入风险、健康状况、商业和自有房产投资等背景风险因素对居民金融资产投资的影响. 邓雄等［21］研究考虑背景风险和弹性增量的模糊投资组合模型，结果表明背景风险的方差越大，则投资组合的收益和投资者的满意度越小，投资组合的方差越大. 李海荣和蔡明超［22］应用Probit模型分析背景风险对居民风险资产投资概率的影响. 李佳等［23］提出考虑交易费用和背景风险的最大期望满意度模型，结果表明投资组合的收益和期望最大满意度均与背景风险呈负相关. 李佳等［24］在考虑交易费用的双目标模型中引入背景风险，研究背景风险和背景风险偏好度大小对投资组合的影响，指出考虑背景风险的投资组合优于不考虑背景风险的投资组合. 后来，一些研究同时关注到加性和乘性背景风险，并研究它们对投资决策的影响. Tsetlin和Winkler［2］通过算例阐述加性背景风险或乘性背景风险对投资决策的影响，并从理论上研究同时考虑两类背景风险情形下相关背景风险对投资的影响. 张尧等［25］研究考虑一类背景风险单独存在和两类背景风险同时存在的项目投资决策问题，分析背景风险与项目风险之间的相关性及相关程度对投资决策的影响. 但是，上述考虑两类背景风险的研究均针对单期投资问题，缺乏考虑两类背景风险的多期投资组合问题的研究.

基于此，本文针对同时面临两类背景风险的情形，研究考虑两类背景风险和破产控制的多期投资组合问题. 以最大化终端财富的期望值和最小化终端财富的方差为目标，将两类背景风险引入投资者财富，对每一期的财富进行破产控制，并通过偏好系数和标准化方法将双目标规划转化为单目标规划. 然后，应用粒子群算法对模型进行求解. 最后，通过实证分析验证两类背景风险对考虑破产控制的多期投资组合的影响.

1 考虑两类背景风险的多期投资组合模型

假设投资者可对n 项资产进行投资，投资期限为T 期. 假设投资者在投资过程中同时面临加性背景风险和乘性背景风险. n 项资产包含两项无风险资产和n-2 项风险资产，其中，风险资产均受乘性背景风险影响，两类无风险资产分别为不受乘性背景风险影响的无风险资产和受乘性背景风险影响的无风险资产.因加性背景风险的不可交易性，投资者在T 个投资期只能接受加性背景风险的损益，不能改变加性背景风险每期期初的财富值. 因此，投资者的财富可整体划分为投资部分财富和加性背景风险部分财富. 在第一阶段，投资者在n 项资产之间分配其投资部分的初始财富. 在剩下的T-1 个阶段，上一期投资部分的期末财富在本期期初重新在n 项资产之间进行分配. 加性背景风险在T 个投资周期内存续. 为方便表述，本文设定符号如下.

Wt、wt和Yt分别表示第t 期期初，投资者的总财富、投资部分的财富和加性背景风险部分的财富；pi,t表示第t 期期初，分配在资产i 的投资额占投资部分总财富的比例；、ry1,t和ry2,t分别表示第t 期资产i 的收益率、加性背景风险的收益率和乘性背景风险的收益率；ri,t表示第t 期考虑背景风险后资产i 的收益率；Rt表示第t 期考虑背景风险后投资部分的组合收益率；和E( ry2,t)分别表示第t 期资产i 的期望收益率、加性背景风险的期望收益率和乘性背景风险的期望收益率；E( Rt)表示第t 期考虑背景风险后投资部分的期望组合收益率；E(WT+1) 表示终端财富的期望值；分别表示第t 期的方差；和分别表示第t 期Rt和终端财富的方差；分别表示第t 期、ry1,t和ry2,t之间的协方差；表示第t 期Rt与ry1,t的协方差；其中i=1,2,…,n，资产1为不受乘性背景风险影响的无风险资产，资产2为受乘性背景风险影响的无风险资产，剩余n-2 项资产均为风险资产；t=1,2,…,T .

参考Eun和Resnick［26］，第t 期，考虑背景风险后各资产的收益率可表示为：

资产1不受背景风险影响，由式（1）可知，资产1考虑背景风险后的收益率还是它本身. 由式（2）和（3）可知，资产i（i=2,3,…,n）考虑背景风险后的收益率由资产本身的收益率和乘性背景风险的收益率组成. 对于投资者而言，由于受到乘性背景风险的影响，资产2实际上也相当于风险资产. 第t 期，考虑背景风险后投资部分的组合收益率可表述为：

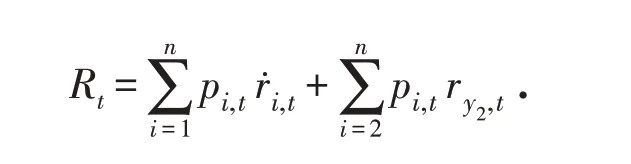
第t 期，投资部分和加性背景风险部分的期末财富可分别表述为：

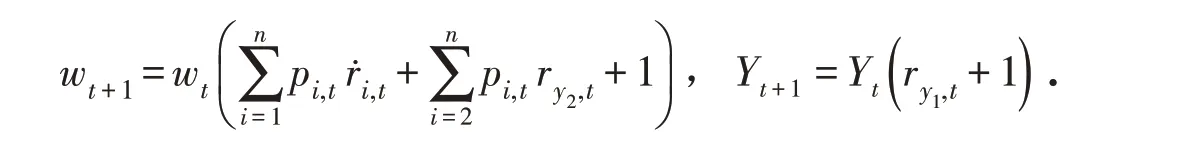
第t 期，投资者的期末总财富可表述为：

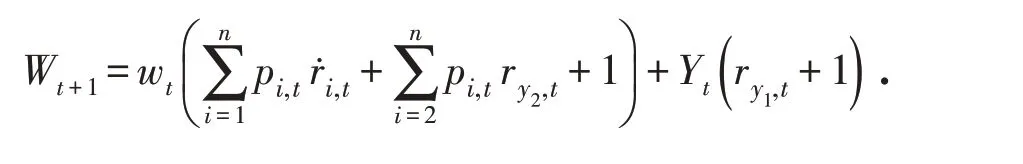
那么，终端财富可表述为：

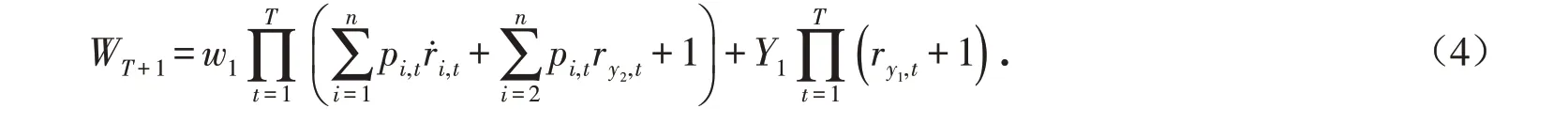
在本文中，投资者的投资目标是在破产控制下，最大化终端财富的期望值和最小化终端财富的方差. 假设投资部分的财富没有额外的资金流入或流出. 假设证券市场是完全有效的，即每个投资者都能充分了解财富形式中每一部分的期望收益率和方差等统计指标，投资对象的信息完全外在表现在其价格中，各期投资组合的组合收益率之间两两不相关. 假设证券市场不存在交易费用和所得税，并且可以以任何单位交易，但是不允许卖空. 由式（4）可得：

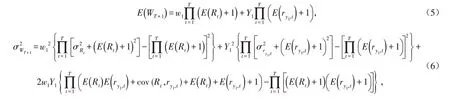
其中：

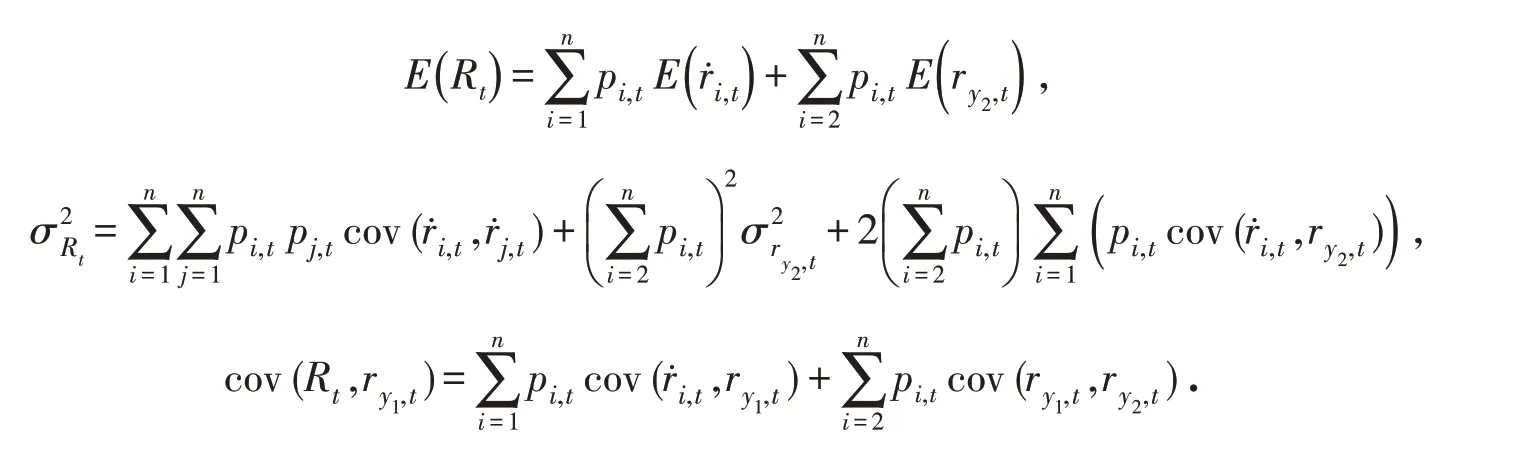
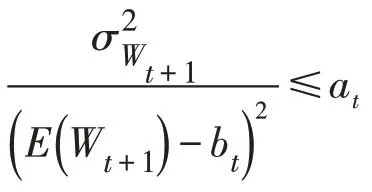
本文的投资目标包括最大化终端财富的期望值和最小化终端财富的方差，则投资者需在式（5）和（6）之间进行权衡. 为避免两个目标量级差距过大带来的影响，本文先对两个目标进行标准化，使两个目标能在同一水平上比较. 然后，通过权衡系数λ 实现投资者在它们之间的权衡. λ 体现投资者的偏好态度，且λ ∈[0 ,1] . 那么，考虑两类背景风险和破产控制的多期均值-方差模型，可表示为如下非线性规划P：

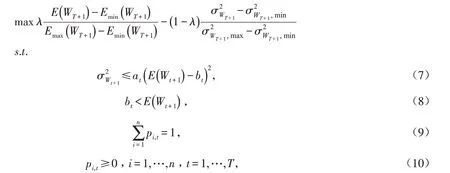
其中：Emax(WT+1) 和Emin(WT+1) 分别为式（7）～（10）约束集下终端财富期望值的最大值和最小值；和分别为式（7）～（10）约束集下终端财富方差的最大值和最小值.

2 粒子群算法

对于上述模型，本文应用粒子群算法进行求解. 在一个D 维空间中，S 个粒子组成一个群落，更新Q 代.在本文中，D=n×T . 第q 代，第s 个粒子通过飞行速度Vs( q )=( vs1( q ),vs2( q ),…,vsD( q ))调整自己的位置Xs( q )=( xs1( q ),xs2( q ),…,xsD( q ))，以此来搜索新解. 经过q 次迭代，第s 个粒子搜索到的最优位置记为ps,best( q )=( ps1( q ),ps2( q ),…,psD( q ))，整个粒子群搜索到的最优位置记为gbest( q )=( g1( q ),g2( q ),…,gD( q )). 通过设定惯性权重w( q )来控制粒子保留原来速度的程度，设定学习因子c1和c2来分别调节个体经验和群体经验的学习程度，r1和r2为[0 ,1] 范围内的随机数. 那么，第s 个粒子根据如下公式分别更新自己的速度和位置：

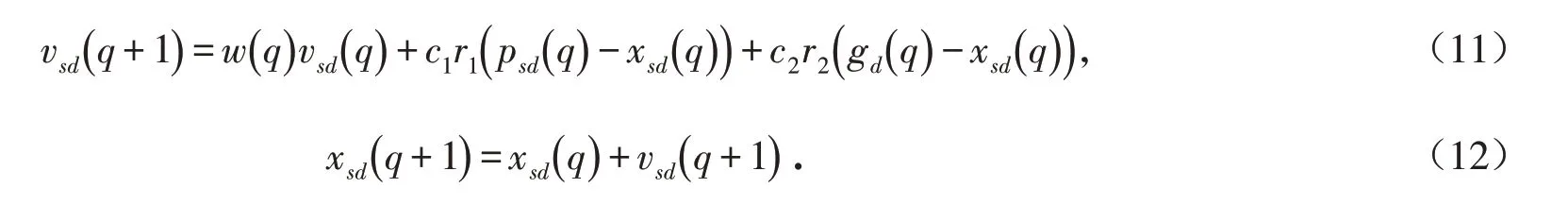
粒子群算法的步骤如下：

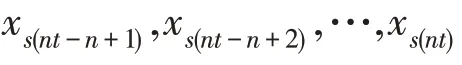
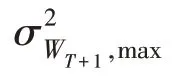
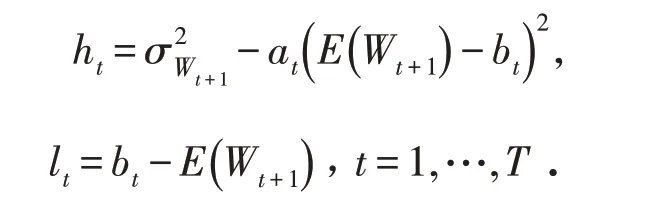
设定惩罚因子M，hmax为h1,h2,…,hT中的最大值，lmax为l1,l2,…,lT中的最大值. 记h˙=max{0 ,hmax} ，l˙=max{0 ,sign(lmax)+1} ，则对应目标函数fk的适应度函数可表示为：

通过式（13）可处理规划P 约束集中的式（7）和（8）.

3）更新ps,best( q )( s=1,2,…,S ). 对于每个粒子，比较它的适应度值和该粒子经历过的最优适应度值，如果此代适应度更优，则个体最优位置更新为本代的位置.

4）更新gbest( q ). 对于每个粒子，比较它的适应度值和整个群体经历过的最优适应度值，如果此代该粒子的适应度更优，则全局最优位置更新为本代该粒子的位置.

5）根据式（11）和（12）更新粒子的速度和位置. 设定最大位置限制xmax、最小位置限制xmin、最大速度限制vmax和最小速度限制vmin. 若更新后vsd＜vmin，则设置vsd=vmin；若更新后vsd＞vmax，则设置vsd=vmax；若更新后xsd＜xmin，则设置xsd=xmin，s=1,2,…,S，d=1,2,…,D . 粒子位置更新后，再一次对每n 个位置分量进行归一化处理.

6）迭代Q 次.

7）重复试验，选取重复试验中的最优结果作为最终结果.

3 实证分析

假设投资者已有对国内风险资产的投资，该投资者现考虑将现有资金在国内无风险资产、国外无风险资产和国外风险资产之间进行分配. 假设在进行新的投资的过程中，投资者不调整已经投资的国内风险资产的头寸. 那么，该投资者在新的多期投资中，将一直面临加性背景风险. 国内正在投资的风险资产的不确定收益即为加性背景风险. 由于投资国外资产，投资者也将一直面临乘性背景风险，汇率风险即为乘性背景风险. 在本文中，采用本国投资者观点，即最终财富以本币为计价单位.

美国标准普尔500指数（SPX）在美国股市具有较强的代表性，中国沪深300指数（000300）能综合反映中国A股市场的整体表现，本文选取它们分别代表国外风险资产和加性背景风险. 选取美元中间价（USDCNY）代表乘性背景风险. 我们使用中国和美国的活期存款利率作为两地的无风险资产收益率. 我们的数据均摘自东方财富Choice数据. 本文选取的研究区间为2018年3月—2018年8月，两个月为一个投资期，共投资三期. 本文假设未来状况可通过历史数据正确反映，两地无风险资产的收益率在三个投资期内是恒定的. 中国活期存款基准年利率为0.35%，美国活期存款年利率为0.36%. 故本文设定一个投资期（2个月）的国内和国外无风险利率分别为0.000 6和0.000 6，它们分别对应r˙1和r˙2. 第t 期SPX、000300和USDCNY 的收益率分别对应、ry1,t和ry2,t( t=1,2,3)，研究期间内剔除交易时间不同的样本点. 三个期间、ry1,t和ry2,t的期望收益和方差，以及他们之间的协方差见表1.

表1 各期统计指标Tab.1 Periods’statistical indexes

本文设定投资部分的初始财富为1，即w1=1. 参考Li等［13］，假定任何可接受的交易策略下，财富期望值在任意一期均大于零，且各期破产概率不超过0.2，即bt=0，at=0.2，t=1,2,3 . 设定粒子群算法的参数如下：S=100，Q=500，c1=2，c2=2，wmax=0.9，wmin=0.4，xmax=1，xmin=0，vmax=0.5，vmin=-0.5，M=10 000. 运算重复10次，取最优解为最终解.

表2显示了不同偏好态度下的多期最优投资策略及其目标值. 由表2可知，随着λ 的增大，国内无风险资产的投资比例减小. 国外无风险资产由于受到汇率风险的影响，实际上相当于风险资产. 投资者对收益的偏好越大，国内无风险资产的投资比例越少，意味着其投资于“风险资产”的比例越大，此时国外无风险资产和国外风险资产的投资比例均越大. 当λ 大到使投资者不再投资于国内无风险资产时，λ 增大，投资于国外风险资产的比例继续加大，而投资于国外无风险资产的投资比例开始减小.

在2015年1月至2019年8月期间内，滑动统计两个月时间长度的000300的方差，其最小值为0.019 1，最大值为2.764 5. 假设的可能值在此区域. 假设投资者面临β 倍的，则β 可为0.2～7.2. 本文选取β 值为0.25、0.5、1、1.5、2，分析不同下投资者的最优投资策略的变化，结果见表3. 由表3可知，若投资者在国内无风险资产上进行投资，当β 增大时，其投资比例将会增大，在其余两个资产上的投资比例之和将减小. 在这种情况下，若投资者在国外风险资产上进行投资，其投资比例随β 的增大而减小. 若投资者不在国内无风险资产上进行投资，当β 增大时，国外无风险资产的投资比例将增大，国外风险资产的投资比例将减小. 此外，Y1越大，投资策略发生的变化越大，即加性背景风险对投资策略的影响越大. 整体而言，投资者面临波动更大的不良加性背景风险( E( ry1,t)＜0 )时，投资者偏向更加保守的投资策略. 在这一点上，与Gollier和Pratt［15］提出的“风险脆弱性”是一致的. 也就是说，在多期投资中，也存在“风险脆弱性”现象. 当投资者面临波动较大的加性背景风险时，破产可能会发生. 如表3中，Y1=0.5 且β=2 时，破产发生，投资者无可行的投资方案，投资者需要更换投资对象才能避免破产.

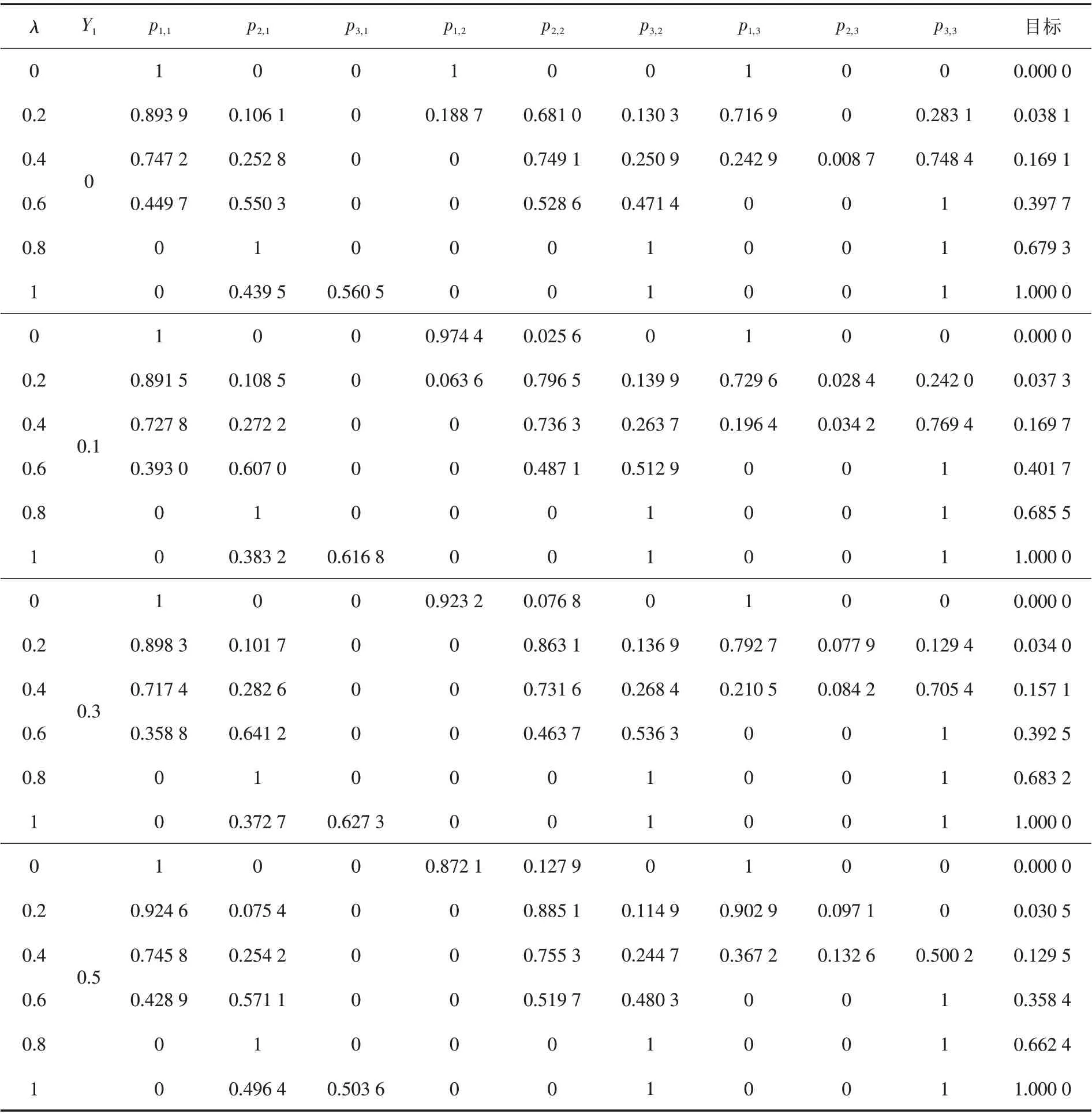
表2 不同偏好态度λ 下的最优投资策略及目标Tab.2 Optimal investment strategy and target with different preference attitudes λ

表3 不同加性背景风险下的最优投资策略及目标Tab.3 Optimal investment strategy and target with different additive background risk 1t

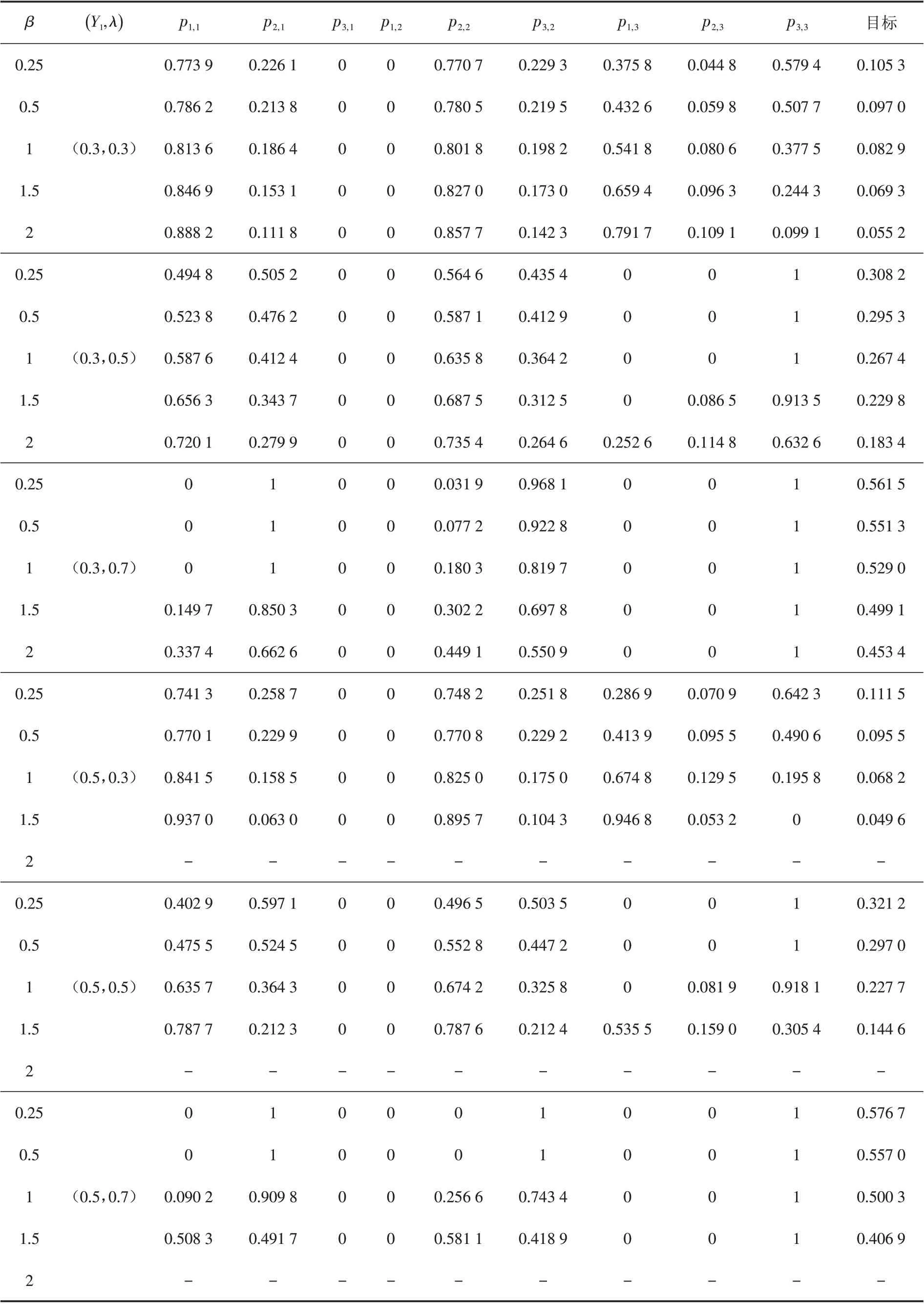
表3 不同加性背景风险下的最优投资策略及目标Tab.3 Optimal investment strategy and target with different additive background risk 1t

注：“-”表示当前投资组合对象下，任何投资方案均发生破产，即无可行的投资方案.

β( )Y1,λ p 1,12,13,11,22,23,21,32,33,3 0.773 90.226 10 0 0.770 70.229 30.375 80.044 80.579 40.105 3 0.786 20.213 80 0 0.780 50.219 50.432 60.059 80.507 70.097 0 0.813 60.186 40 0 0.801 80.198 20.541 80.080 60.377 50.082 9 0.846 90.153 10 0 0.827 00.173 00.659 40.096 30.244 30.069 3 0.888 20.111 80 0 0.857 70.142 30.791 70.109 10.099 10.055 2 0.494 80.505 20 0 0.564 60.435 40 0 1 0.308 2 0.523 80.476 20 0 0.587 10.412 90 0 1 0.295 3 0.587 60.412 40 0 0.635 80.364 20 0 10.267 4 0.656 30.343 70 0 0.687 50.312 500.086 50.913 50.229 8 p p p p p p p p 0.25 0.5 1 1.5 2 0.25 0.5 1 1.5 2 0.25 0.5 1 1.5 2 0.25 0.5 1 1.5 2 0.25 0.5 1 1.5 2 0.25 0.5 1 1.5 2目标0.720 10.279 90 0 0.735 40.264 60.252 60.114 80.632 60.183 4 0 1 0 0 0.031 90.968 10 0 1 0.561 5 0 1 0 0 0.077 20.922 80 0 1 0.551 3 0 10 0 0.180 30.819 70 0 1 0.529 0 0.149 70.850 30 0 0.302 20.697 80 0 1 0.499 1 0.337 40.662 60 0 0.449 10.550 90010.453 4 0.741 30.258 70 0 0.748 20.251 80.286 90.070 90.642 30.111 5 0.770 10.229 90 0 0.770 80.229 20.413 90.095 50.490 60.095 5 0.841 50.158 50 0 0.825 00.175 00.674 80.129 50.195 80.068 2 0.937 00.063 00 0 0.895 70.104 30.946 80.053 20 0.049 6--- - --- - - -0.402 90.597 10 0 0.496 50.503 50 0 1 0.321 2 0.475 50.524 50 0 0.552 80.447 20 0 10.297 0 0.635 70.364 3000.674 20.325 800.081 90.918 10.227 7 0.787 70.212 30 0 0.787 60.212 40.535 50.159 00.305 40.144 6- - - - - - - - - -0 1 0 0 0 1 0 0 1 0.576 7 0 10 0 0 1 0 0 1 0.557 0）0.090 20.909 80 0 0.256 60.743 40 0 1 0.500 3 0.508 30.491 70 0 0.581 10.418 90 0 1 0.406 9----------（0.3，0.3）（0.3，0.5） （0.3，0.7）（0.5，0.3）（0.5，0.5）（0.5，0.7

表4 不同乘性背景风险下的最优投资策略及目标Tab.4 Optimal investment strategy and target under different multiplicative background risk 2

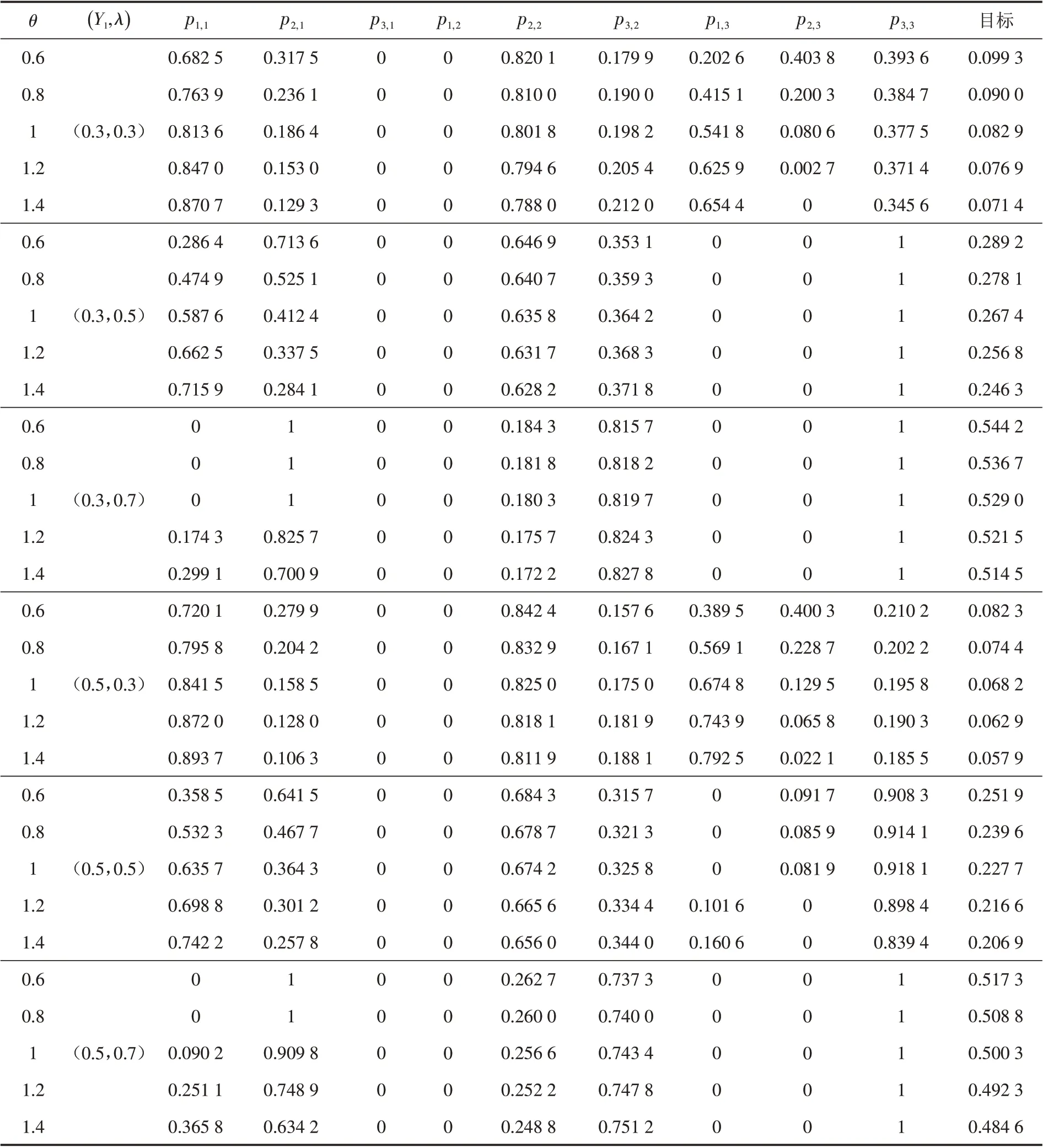
表4 不同乘性背景风险下的最优投资策略及目标Tab.4 Optimal investment strategy and target under different multiplicative background risk 2

θ(Y 1,λ)p1,1p2,1p3,1p1,2p2,2p3,2p1,3p2,3p3,3目标0.60.682 50.317 50 0 0.820 10.179 90.202 60.403 80.393 60.099 3 0.80.763 90.236 10 0 0.810 00.190 00.415 10.200 30.384 70.090 0 1（0.3，0.3）0.813 60.186 40 0 0.801 80.198 20.541 80.080 60.377 50.082 9 1.20.847 00.153 00 0 0.794 60.205 40.625 90.002 70.371 40.076 9 1.40.870 70.129 30 0 0.788 00.212 00.654 40 0.345 60.071 4 0.60.286 40.713 60 0 0.646 90.353 10 0 1 0.289 2 0.80.474 90.525 10 0 0.640 70.359 30 0 1 0.278 1 1（0.3，0.5）0.587 60.412 40 0 0.635 80.364 20 0 1 0.267 4 1.20.662 50.337 5 0 0 0.631 70.368 30 0 1 0.256 8 0 0 0.628 20.371 80 0 1 0.246 3 0 0 0.184 30.815 70 0 1 0.544 2 0 0 0.181 80.818 20 0 1 0.536 7 0 0 0.180 30.819 70 0 1 0.529 0 000.175 70.824 30010.521 5 1.40.715 90.284 1 0.6 0.8 1 1.2 1.4 0.6 0.8 1 1.2 1.4 0.6 0.8 1 1.2 1.4 0.6 0.8 1 1.2 1.4（0 .3，0.7）01 0.174 30.825 7 0.299 10.700 90 0 0.172 20.827 80010.514 5 0.720 10.279 90 0 0.842 40.157 60.389 50.400 30.210 20.082 3 0.795 80.204 20 0 0.832 90.167 10.569 10.228 70.202 20.074 4.5，0.3）0.841 50.158 50 0 0.825 00.175 00.674 80.129 50.195 80.068 2 0.872 00.128 00 0 0.818 10.181 90.743 90.065 80.190 30.062 9 0.893 70.106 30 0 0.811 90.188 10.792 50.022 10.185 50.057 9 0.358 50.641 50 0 0.684 30.315 70 0.091 70.908 30.251 9 0.532 30.467 70 0 0.678 70.321 30 0.085 90.914 10.239 6.5，0.5）0.635 70.364 30 0 0.674 20.325 800.081 90.918 10.227 7 0.698 80.301 20 0 0.665 60.334 40.101 60 0.898 40.216 6 0.742 20.257 80 0 0.656 00.344 00.160 60 0.839 40.206 9 0 1 0 0 0.262 70.737 30 0 1 0.517 3 0 10 0 0.260 00.740 00 0 1 0.508 8.5，0.7）0.090 20.909 80 0 0.256 60.743 40 0 1 0.500 3 0.251 10.748 90 0 0.252 20.747 80 0 1 0.492 3 0.365 80.634 2000.248 80.751 20010.484 6 0 0 1 1（0（0（0

4 结论

本文将两类背景风险引入多期投资组合问题，构建考虑破产控制的多期均值-方差模型，并应用粒子群算法进行求解. 最后，通过实证分析检验了两类背景风险对多期最优投资策略的影响. 整体而言，若投资者在国内无风险资产上进行投资，则随着两类背景风险的增加，投资者将增加国内无风险资产的投资比例. 在多期投资中，加性背景风险的波动增大，也会导致“风险脆弱性”现象的出现，投资者将进行更加保守的投资策略. 乘性背景风险的波动变化时，投资者的最优投资策略也会发生变化，投资者需根据资产和乘性背景风险之间的相关性来进行投资策略的调整. 由于两类背景风险对多期最优投资策略有显著影响，故将两类背景风险引入考虑破产控制的投资组合选择模型是实际而且重要的.