基于灰色-马尔可夫模型的国内游客总数预测
2020-04-01张冬咏陈泗达
张冬咏, 陈泗达
(河南农业大学信息与管理科学学院,郑州 450002)
旅游业作为绿色无烟产业,是我国非贸易外汇收入的主要来源之一和经济发展的支柱性产业之一[1].根据文化和旅游部2019 年2 月12 日发布的《2018 年旅游市场基本情况》(http://zwgk.mct.gov.cn/auto255/201902/t20190212_837271.html?keywords=),我国旅游业对GDP的贡献额度持续增长,2018年旅游业对GDP总量的综合贡献为9.94 万亿元,占据GDP 总量的11.04%. 此外,自我国经济转型以来,经济发展迈入新常态,第一、二产业的发展相对放缓,以商品和服务为主的第三产业对经济增长的拉动作用更为明显. 因此,作为第三产业重要组成部分之一的旅游业,在对外开放、促进消费、乡村振兴、精准扶贫以及“一带一路”等方面的建设中扮演着重要角色,并且成为拉动消费、推动供给侧结构改革的新的经济增长点[2].
在旅游业的营销、运营以及战略制定中,游客总数是一个重要指标,科学准确地预测未来游客总数能够有助于相关部门与企业把握游客增长趋势,从而制定合理的方案策略. 通过文献研究,发现目前对未来游客总数的预测方法主要包括时间序列[3-5]、BP神经网络[6]、灰色模型[7-8]、马尔可夫模型[9]和组合模型[10-11]等. 不同的预测方法有不同的优缺点及适用范围,它们之间并非相互排斥,而是可以组合以增加适用性及预测精度[11]. 通过上述文献,发现组合模型凭借模型之间的优势互补,已经越来越多的应用于预测研究. 如雷可为和陈瑛基于BP神经网络和ARIMA模型构建了组合模型,预测结果证明组合模型相比于单一的预测方法预测精度更高;梁昌勇等构建了SVR-ARMS模型,通过对比单一的SVR模型和ARMA模型后认为组合模型拥有更高的预测精度;陈美璘和何清龙基于Logistic模型、灰色模型、对数线性模型和熵权法提出了混合预测模型,实验结果证明混合预测模型的拟合效果更优;王洋和张萍构建了IOWA组合模型,通过对比灰色模型、三次指数平滑模型和BP神经网络模型后认为组合模型的预测精度更高.
基于我国旅游业发展时间短和发展速度快的特点,本文结合灰色模型和马尔可夫模型的优点构建组合模型. 灰色GM(1,1)侧重于研究有限信息下事物变化的趋势,克服了传统预测模型需要大样本数据的瓶颈制约,具有小样本下预测精度较高的优点,然而其预测结果为平滑曲线,很难反应数据的波动状态,因此对波动较大的数据的拟合结果较差. 马尔可夫模型则侧重于研究随机波动性较大的动态过程,根据状态之间的转移概率来预测系统未来的发展情况,因此能对随机波动序列进行长期预测. 本文结合二者优点,构建灰色-马尔可夫模型,选取2004—2018年国内游客总数的相关数据,并以2004—2015年的国内游客总数为基础构建模型,预测2016—2018年的国内游客总数,通过对预测值与实际值的比对,说明组合模型的优化程度.
1 灰色马尔可夫模型
1.1 传统灰色GM(1,1)模型
由于原始数据存在不确定性及各种冲击扰动因素,因此在利用传统灰色GM(1,1)模型进行预测时,常常需要对原始数据进行处理,并根据情况进行强化或弱化的转变,形成新的数据序列.
假设原始数列为:

则其一次累加序列1-AGO为:

其中,
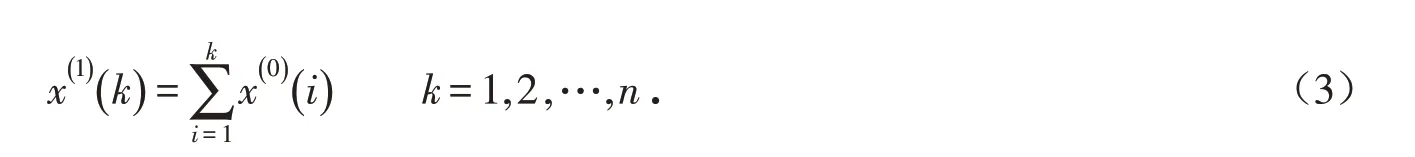
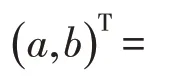

式中:x(1)为一次累加序列;t 为时间;a 和b 为估计参数,其中a 为发展系数,b 为灰色作用量. ,且B Y 的具体表达式为:
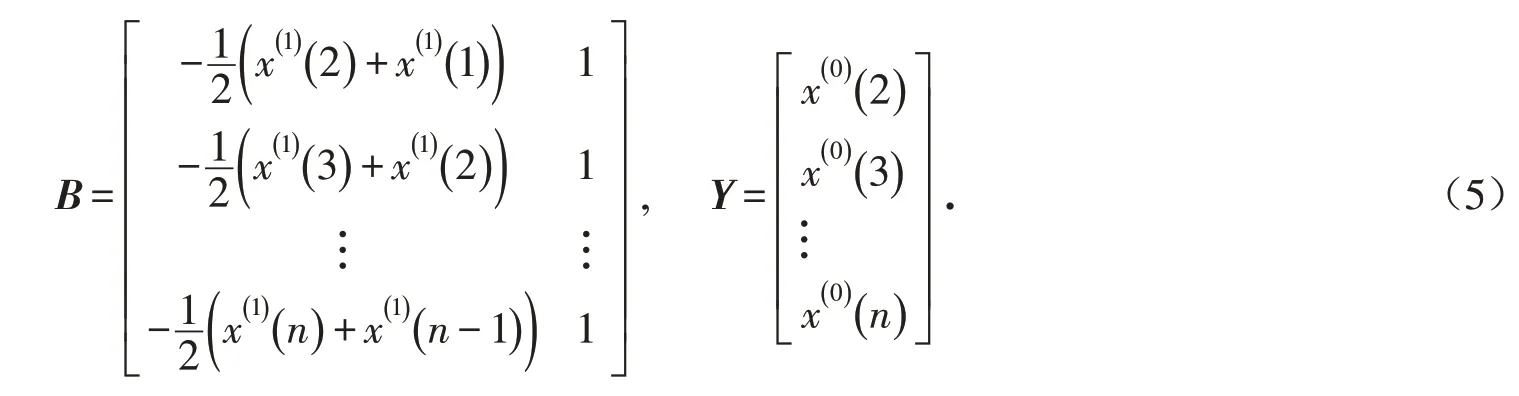
由此,可以得出微分白化方程的解为:

同时,可以得出传统灰色GM(1,1)模型的预测表达式为:

1.2 无偏灰色GM(1,1)模型
基于传统灰色GM(1,1)模型中的估计参数a,b 的值,可以得到无偏灰色GM(1,1)模型中的估计参数α,β 的值,其计算过程为:

因此,无偏灰色GM(1,1)模型的预测表达式为:

1.3 基于马尔可夫模型的GM(1,1)模型优化
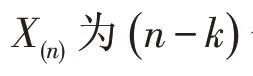

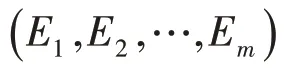
2)状态转移概率矩阵的构造. 状态转移概率以pij表示,代表从状态Ei转变为状态Ej的概率,由此可以得到状态转移概率矩阵:

式中:pij=Mij/Mi,Mi表示状态Ei的总次数;Mij表示状态Ei转变为状态Ej的总次数.

2 实证分析
2.1 数据来源
本文选取国内游客总数作为研究对象,自国家统计局网站(http://data.stats.gov.cn/)摘录2004—2018年国内游客总数的具体数值,以2004—2015 年数据作为基础构建模型,拟合2016—2018 年的国内游客总数,并对实际值与各模型的预测值进行对比分析.
2.2 传统和无偏灰色GM(1,1)模型构建及检验
通过上述模型进行数据演算,得到传统GM(1,1)模型的估计参数:a=-0.12,b=102 180.05,因此根据式(7)得到传统灰色GM(1,1)模型的预测表达式为:

同时,通过式(8)和式(9)得到无偏灰色GM(1,1)模型的预测表达式为:
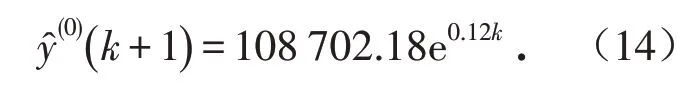
预测模型构建后需要对其进行残差检验和后验差检验,只有当检验合格之后才能进行预测,否则说明模型预测无效.在残差检验中,传统和无偏灰色GM(1,1)模型平均相对误差均为2.54%,模型精度均为97.46%,参照表2 发现模型精度等级达到二级;在后验差检验中,均方差比均为0.08,小误差概率分别均为1,精度等级达到一级. 综上所述,传统和无偏灰色GM(1,1)模型检验通过,可以进行预测.
2.3 基于马尔可夫模型的结果优化
1)状态的划分. 通过式(13)、(14)得到2004—2015 年的国内游客总数的拟合结果,以相对精度划分为高估、合理和低估3种状态(表3). 以传统GM(1,1)模型为例,相对精度范围为0.94至1.05,故高估状态E1=[0.94,0.98),合理状态E2= [0.98,1.02)和低估状态E3=[1.02,1.05]. 同理,无偏灰色GM(1,1)模型的状态划分为:高估状态E1=[0.94,0.98),合理状态E2=[0.98,1.02)和低估状态E3=[1.02,1.05] .
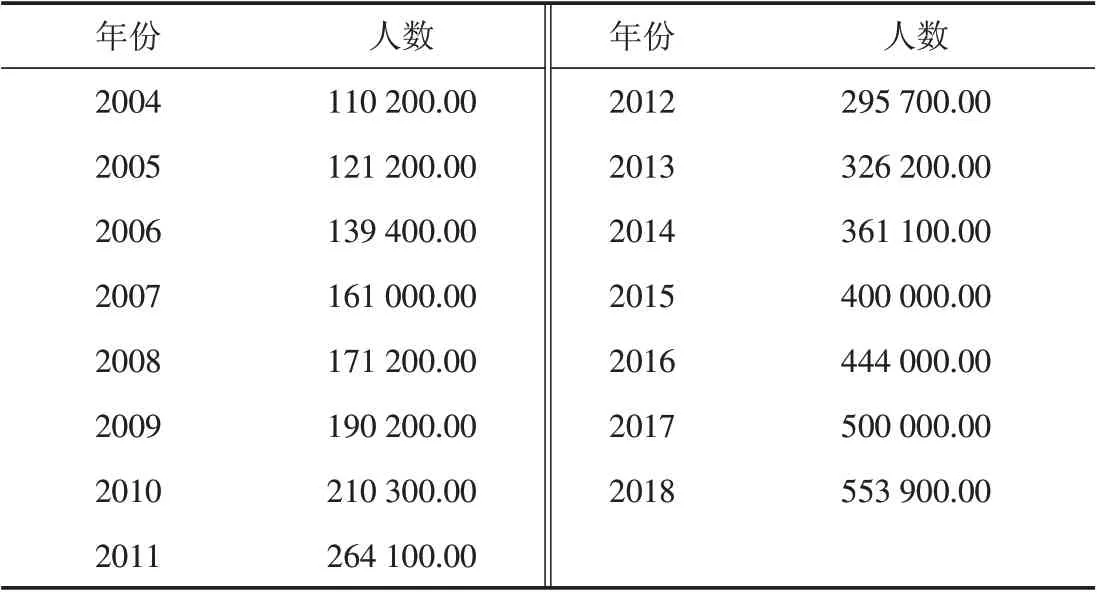
表1 2004—2018年国内游客总数 单位:万人Tab.1 Total domestic tourists from 2004 to 2018
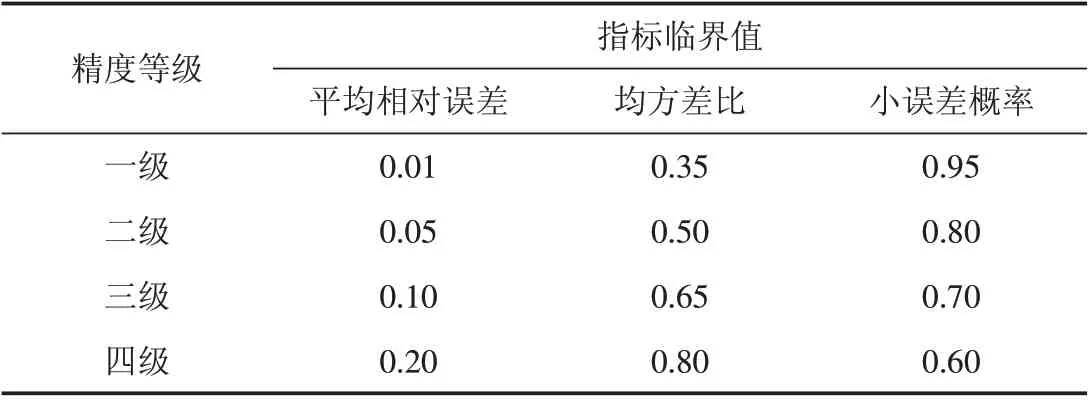
表2 精度等级校验参照表Tab.2 Reference table for accuracy level calibration
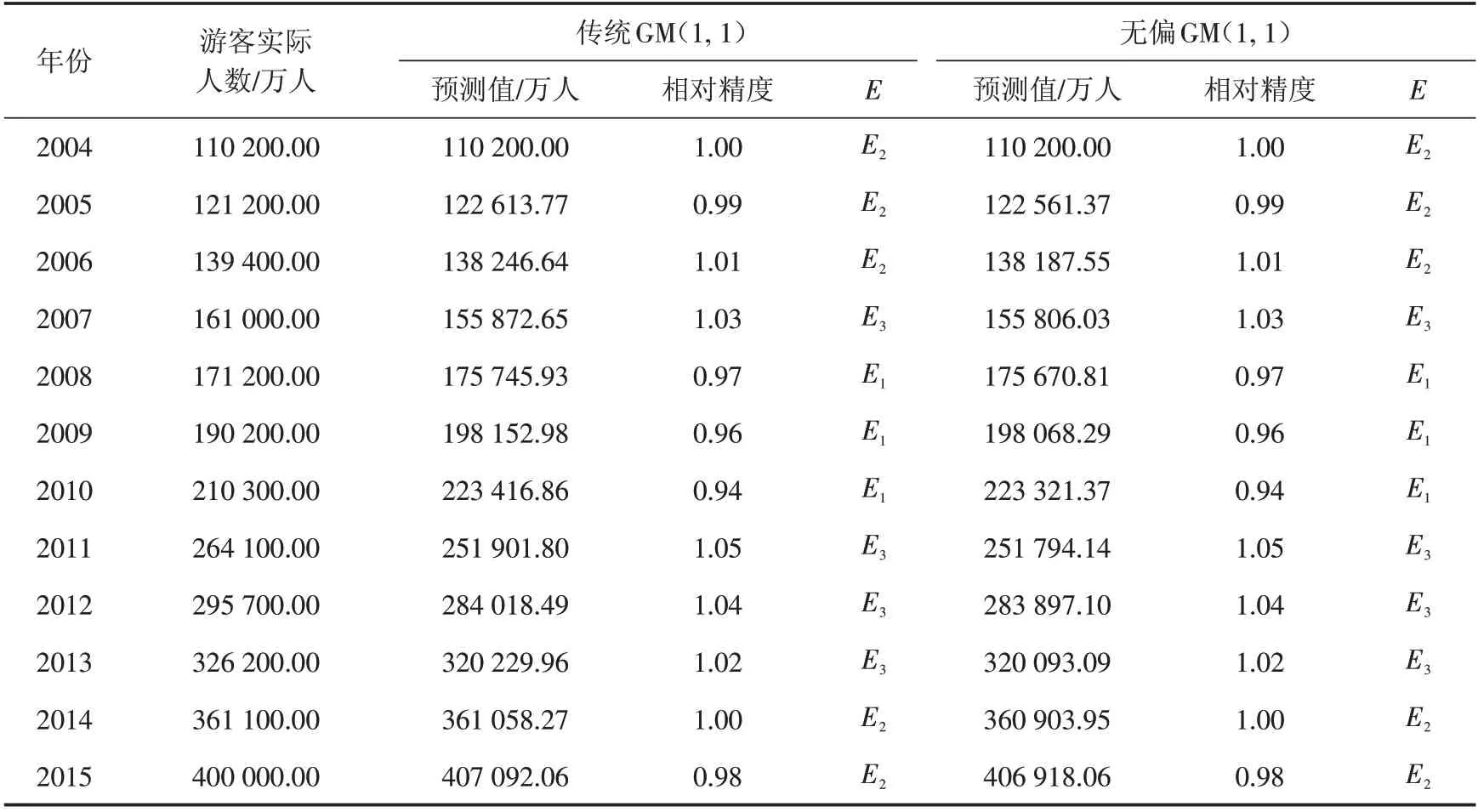
表3 传统和无偏灰色GM(1,1)模型的拟合结果和状态划分Tab.3 Fitting results and state division of traditional and unbiased gray GM(1,1)models
2)状态转移概率矩阵的构造. 假设传统和无偏灰色GM(1,1)模型的状态转移概率矩阵分别为P1与P2. 以P1为例,状态E1共出现3 次,状态E2共出现5 次,状态E3共出现4 次,且从状态E1转变为状态E1E2E3的次数分别为2次、0次和1次;从状态E2转变为状态E1E2E3的次数分别为0次、3次和5次;从状态E3转变为状态E1E2E3的次数分别为1次、1次和2次,因此得到状态转移概率矩阵P1. 同理,得到状态转移概率矩阵P2.
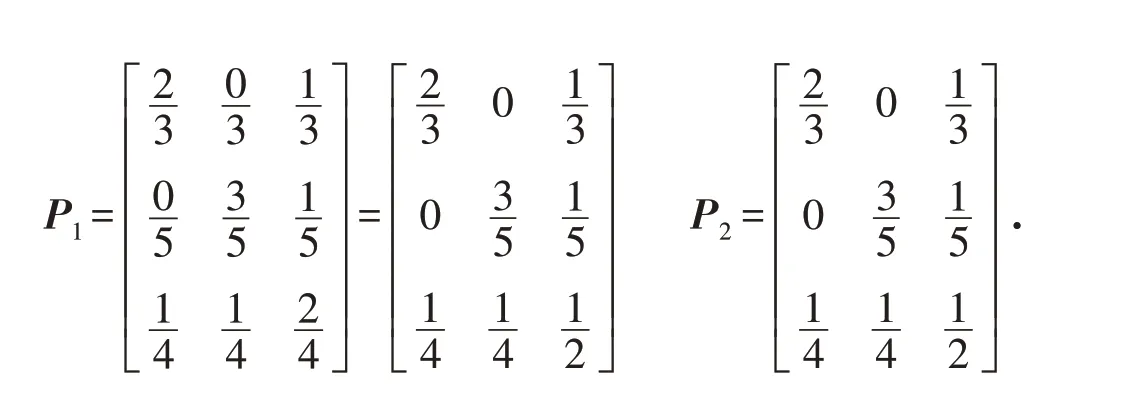
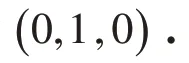
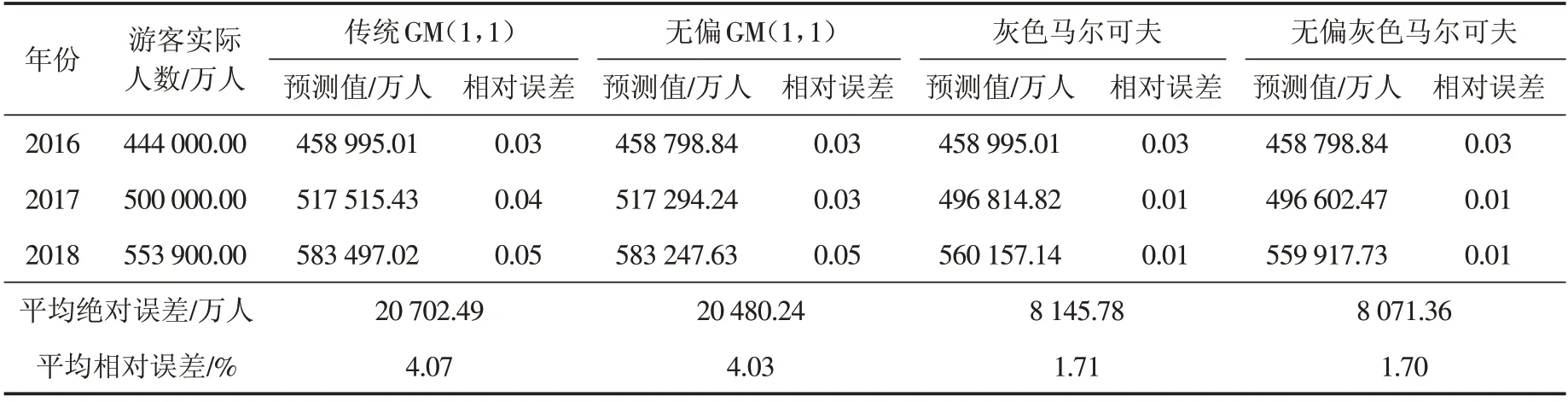
表4 预测结果对比分析Tab.4 Comparative analysis of prediction results
通过对比发现,灰色马尔可夫模型和无偏灰色马尔可夫模型的平均绝对误差分别为8 145.78和8 071.36,平均相对误差分别为1.71%和1.70%. 相比于传统的灰色模型而言在精度上有显著提高,平均相对误差分别提高了2.36%和2.33%. 结果表明,灰色GM(1,1)模型可以有效结合马尔可夫模型,并且能够较好地提高对波动数据的预测精度.
3 结语
近年来旅游业逐渐成为我国GDP的重要组成部分,国内旅游市场的游客人数往往受到各种因素(如政策、舆论等)的影响而产生一定波动,因此精准预测游客人数能够有效帮助相关部门做好战略决策. 本文以2004—2015年国内游客总数为基础,基于灰色模型能够在有限信息进行有效预测的优势以及马尔可夫模型能够对波动数据进行精准预测的优点,将两者结合构建模型,研究发现两者组合后的模型能够有效改善灰色模型对随机波动数据的预测精度,并通过对比2016—2018年国内游客总数的实际值与预测值,以实际数据表明,结合马尔可夫模型后的灰色组合模型的预测精度显著高于单一灰色模型下的预测精度.
