基于退火加速的差分进化算法改进及应用

陈怡君， 刘军民

（1.西安航空学院，西安 710077； 2.西安交通大学数学与统计学院，西安 710049）

在理论研究和实际应用过程中经常会遇到大量的复杂优化问题，对于那些不可微、非线性函数的优化尤为困难［1-2］. 传统的优化方法大多需要计算目标函数的导数值以及其他一些辅助信息来确定搜索方向，且对函数的凸性、线性等有诸多限制，求解过程易于陷入局部最优，而工程实际中目标函数不可微或不能用函数表示的现象经常存在，因此传统优化技术虽然具有较强的局部搜索能力，但对于复杂函数的优化却不能得到满意的结果［3-4］.

20世纪80年代以来发展的智能优化算法，如遗传算法、模拟退火算法和粒子群优化算法等，都有很好的性能，这些智能优化算法具有隐并行性、无须导数信息和全局优化等，具有很好的求解复杂优化问题的潜力［5-7］.在众多的智能优化算法中，差分进化算法表现突出，显示了极大的优势，它被证明是1996年IEEE进化算法竞赛中速度最快的进化算法［8］，但是和其他智能优化算法一样，DE算法也存在局部搜索能力不强的缺点［9-11］. 针对这一问题，已有一些改进策略，如与蚁群搜索算法的混合［12］和遗传算法混合［13-15］，还有与序列二次规划算法相结合等［16-17］. 虽然这些算法对提高DE算法的性能有很大改进，但是这些改进策略有的利用了目标函数的导数信息，有的只是针对一类特殊问题而做的改进，因此改变了DE算法原有的通用性及无须导数信息等良好性能［18-19］.

针对上述问题，本文在基本差分进化算法的基础上，对每一个个体以退火概率，用具有较强局部搜索能力的Hooke-Jeeves算法加速，以增强DE算法的局部开发能力，从而显著加快了收敛速度.

1 Hooke-Jeeves算法描述

1961年，Hooke和Jeeves率先提出了Hooke-Jeeves算法（又称为模式搜索法或步长加速法）［20］，该算法的基本思想是利用函数值去构造局部主轴方向，从而尽快找到极小点. 此外，它还具有明显的几何意义，它相当于从山岭某处出发，寻找具有较小函数值的“山谷”，力图使迭代产生的序列沿“山谷”走向逼近极小点.Hooke-Jeeves 算法的计算步骤主要由两大部分组成：一是围绕基点的局部探测，简称为探测移动；二是沿有利的方向向前移动，简称为模式移动，具体操作如下.

1.1 探测移动

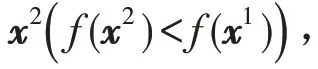
1.2 模式移动

模式移动是指沿两个相邻基点连线方向进行. 在第k 步可行解xk探测移动后得到新的基点xk+1，则作模式移动：

其中：β为加速因子，β ＞0 .

步长加速法是一种直接寻优的确定性方法，形象直观，易于理解和掌握，对目标函数要求甚少，适用范围广泛.

2 退火加速策略

在差分进化算法的进化过程中，常常会出现算法早熟收敛现象，这是因为随着进化的进行，所有个体均向最优个体靠拢，群体的多样性会逐渐消失. 如果最优个体是一全局最优点，则所有个体均收敛到全局最优点，但如果最优个体为一局部最优点，则所有个体均收敛于局部最优点，就会导致早熟收敛. 出现所有个体向最优个体靠拢的原因是差分进化算法的“贪婪”选择机制，这样虽然会加速收敛速度，但同时也会以较大的概率丢弃在全局最优点附近却适应度暂时较差的个体.

鉴于上述分析，在进化的初期应对每个个体以较小的概率加速，以保持其多样性不丧失，保证全局收敛；在后期应该增加每个个体的局部搜索能力，进而提高精度. 所以，对每个个体用以下概率p=t/Tmax（t和Tmax分别是当前的进化代数和设定的最大进化代数）来判断是否利用模式搜索加速. 当随机数小于p 时对个体加速，大于时则不加速. 从p 的表达式可知其在初期值较小，后期值较大，这有点类似于模拟退火概率，符合上述分析的要求，兼顾全局搜索和局部搜索的平衡.

3 算法的描述

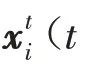
1）初始化参数：种群规模NP；缩放因子F ；变异因子CR；空间维数D；加速因子β ；进化代数t=0 .（这里的初始化参数均为标量）.

3）个体评价：计算每个个体的适应度值.

4）变异操作：按下式计算

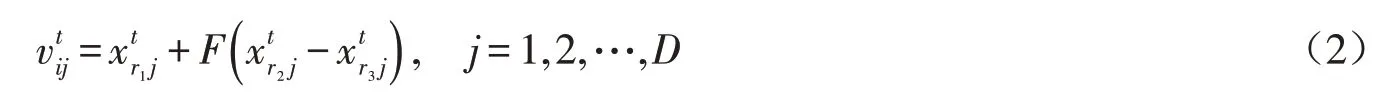
5）交叉操作：按下式计算

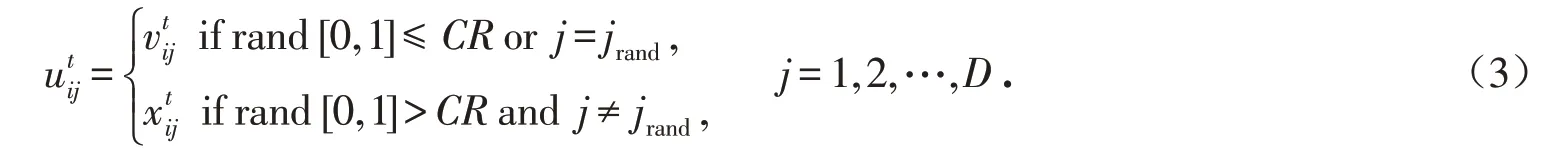
①给出计算精度ε ＞0，初始向量组：e1,e2,…,eD（通常取为各坐标轴上的单位向量）. 初始步长d1=d2=d3=…=dD=d ＞0，加速因子

⑤如果d ≤ε，则计算结束，取x*≈xk；否则，令d=d/2，y1=xk,xk+1=xk,k=k+1，再令j=1，返回②.

8）终止检验：如果达到最大进化代数或满足误差要求，则输出最优值；否则转3）.

4 数值实验及结果分析

下面通过几个典型函数的数值实验来比较本节算法的优劣. 实验要测试的函数如下.1）Sphere Model

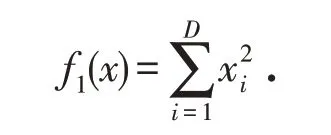
2）Rosenbrok function

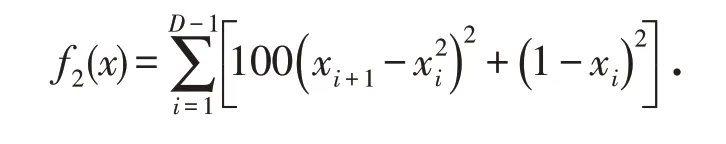
3）Rastrigin Function

4）Grienwank Function

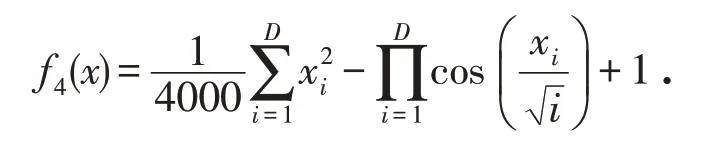
DE算法有四个主要参数：种群规模NP=25；缩放因子F=0.5；变异因子CR=0.1；空间维数D=10 . 在实验中，每个函数的特性和其他参数如表1所示.

表1 各函数的参数设置及特征说明Tab.1 Parameter setting and characteristic description of each function

在测试中，用DE和改进的差分进化算法（简记为MDE）分别随机连续运行20次，其结果见表2.

表2 计算结果比较Tab.2 Comparison of calculation results

图1～4是两种算法的优化曲线比较图. 大图为测试函数的平均最优值在整个迭代过程中的进化情况；小图为后期进化情况优化曲线的放大图. 图中的虚线（蓝色）为基本差分进化算法，实线（红色）为本文提出的算法.

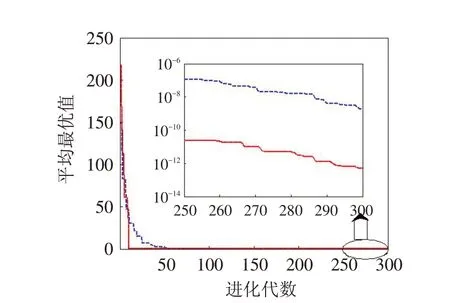
图1 函数f1 的寻优曲线Fig.1 Optimization curves of function f1

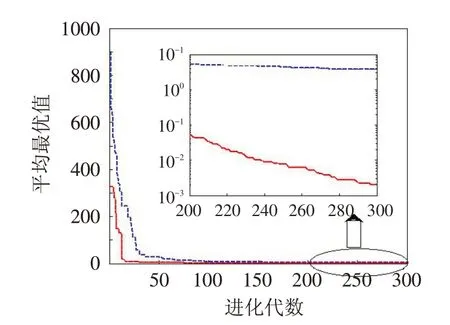
图2 函数f2 的寻优曲线Fig.2 Optimization curves of function f2

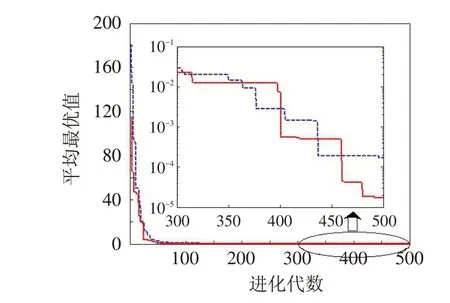
图3 函数f3 的寻优曲线Fig.3 Optimization curves of function f3

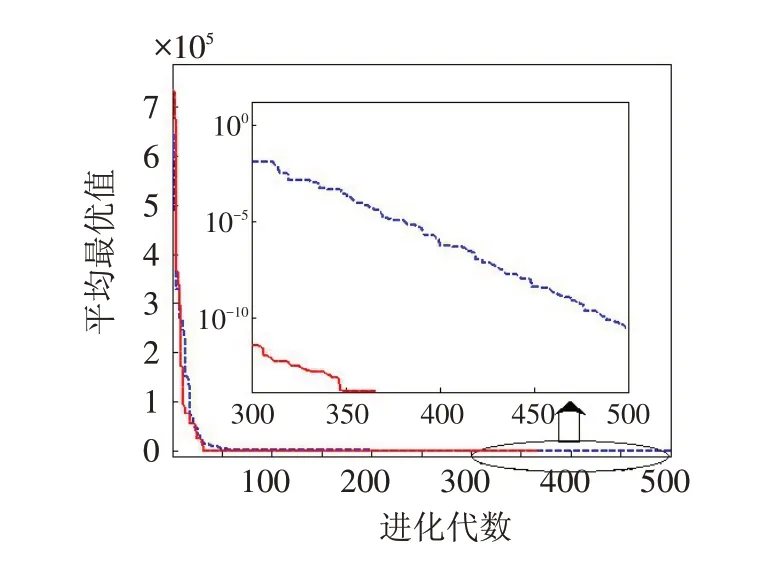
图4 函数f4 的寻优曲线Fig.4 Optimization curves of function f4

由表2和图1～4可知，基于退火加速的差分进化算法的收敛速度比基本的差分进化算法快，尤其是后期由于采用退火加速策略，后期的收敛速度明显加快了. 此外由于较好地保持了多样性，全局搜索能力也得到了加强，精度显著提高.

5 结论

DE算法在求解单目标及多目标优化、约束优化和动态优化等复杂优化问题领域有着极为广泛的研究和应用价值. 本文针对DE算法存在的收敛早熟及收敛速度慢等问题，在传统DE算法的基础上，对每一个个体均具有较强局部搜索能力的Hooke-Jeeves算法加速，以退火概率来增强DE算法的局部开发能力，提出了基于退火加速的差分进化算法. 数值实验结果表明，与传统DE算法相比，该算法收敛速度快、精度高，在保持较好多样性的同时显著加强了全局搜索能力，是一种有效的全局优化算法.