大口径天然气长输管道状态空间模型的适用性分析

殷雄，温凯*，谢萍，闪向营，夏子杰，宫敬*

1 中国石油大学(北京)城市油气输配技术北京市重点实验室，北京 102249 2 中石油管道有限责任公司西部分公司，乌鲁木齐 830013*通信作者, ydgj@cup.edu.cn, kewin1983@126.com

1 天然气管道流动计算模型介绍

管道是长距离运输天然气的主要设备，天然气管道系统是由多个压气站及其调节单元组成的高度非线性、强耦合、大时滞分布参数系统。天然气管道内气体的流动可以用连续性方程、运动方程、能量方程、气体状态方程等非线性偏微分方程组来描述。要求出该方程组的解析解是非常困难，工程应用中一般只求得方程组的近似解或数值解。数值解法主要是通过特征线法、隐式中心法等将偏微分方程转化成差分方程求解管内气体流动状态分布和动态变化过程。这些方法可以直接服务于天然气管道的设计计算、流动分析等各个方面。但是这些方法的计算效率较低，并不适合状态估计、实时优化之类的天然气管道在线应用，无法满足管道实时控制的要求。

1984年，Kralik[1]等提出一种简化的天然气管道传递函数模型，探讨了管道控制偏微分方程通过隐式中心差分空间离散而引入的误差，研究结果可以提高复杂天然气管道的计算效率。虽然Kralik仅仅把这种方法用于天然气管道离线仿真，但是却为传递函数的在线应用提供了新思路。其他学者提出液体管道传递函数模型并在频域进行分析，随后传递函数模型被用于水管道的泄漏检测。2006年，Reddy[2]等引用Kralik提出的天然气管道传递函数模型用于分输量发生变化的在线状态估计和管道破裂的在线泄漏检测。2010年，Behbahani-Nejad[3]等采用二阶传递函数在MATLAB-Simulink中构建了用于模拟天然气管道中流体运动的模型。由于传递函数模型不适用于具有复杂拓扑结构的天然气管道，而状态空间模型可以很好地解决这一问题，Behbahani-Nejad[4]等进一步通过传递函数得到天然气管道的状态空间模型。2012年，Alamian[5]等推导了不同边界条件下天然气管道传递函数，并且得到不同边界条件约束的状态空间模型。2015年，K.A.Pambour[6]等针对天然气管网的仿真控制提出了一种集总参数瞬态模型。2015年，R.Whalley[7]等建立了天然气长输管道的分布式参数模型，通过鲁棒控制算法提出了一种闭环优化调控策略。同在2015年，S.E.Mohammed[8]等提出了一种基于网络分析与仿真的管道状态评价模型。2016年，刘亚龙[9]等提出了一种基于自适应渐进约束参量和控制目标函数的控制模型。Wen[10]的研究表明集总参数状态空间模型是对传递函数模型的改进，去掉了控制直通项，使方程的响应过程更接近于实际管道。

本文采用机理建模的方法，通过天然气管道流动的基本方程推导建立状态空间模型。一般仿真模型都是从管道的偏微分方程组通过数值解法求解，本文提出用状态空间模型对管道水力进行建模分析。状态空间模型是一种集总参数模型，在机理建模的基础上将系统简化为状态量、输入和输出3类变量。通过综合空间变量个数，实现在保证计算精度的同时提高计算效率。状态空间模型不仅可用于实时控制，还能够良好的体现管道本身的非线性、大时滞等特性。对于仿真模型，时间上和空间上的划分精细程度，通常对仿真结果有很大影响。同时由于在建模过程中进行了一定的近似和线性替换，所以需要对模型的适用范围进行分析。为展示模型的实用性，本文选定管径1016 mm的天然气管道作为研究对象。

2 天然气管道的状态空间模型

状态空间模型依据管内气体动力学方程进行推导，其中有2处简化假设：(1)输送过程中气体温度场变化忽略不计；(2)忽略动量方程中对流项的影响。以下推导以刚性管道的一元流动为基础，针对控制体的动力学方程，即连续性方程、运动方程和能量方程[11]，加上气体状态方程构成方程组(1)。

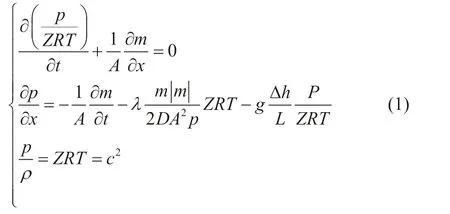
式中：m为气体的质量流量，kg/s；p为气体的压力，Pa；A为管道流通截面面积，m2；ρ为气体的密度，kg/m3；D为管道内径，m；g为重力加速度，m/s2；Δh为管道与水平面的垂直高度，m；L为管道的长度，m；R为气体常数，kJ/(kg·K)；λ为管道水力摩阻系数；Z为气体压缩因子；c为气体的波速，m/s；x为管道位置变量，m；t为时间变量，s。

天然气长输管道中气体运行大多在阻力平方区，摩阻系数λ可以通过科尔布鲁克公式计算，也可以用由Hofer(Hofer，1973)[12]得到的适用于阻力平方区的近似显式公式(2)计算；当气体确定，压缩因子Z是气体压力和温度的函数，可通过公式(3)计算。

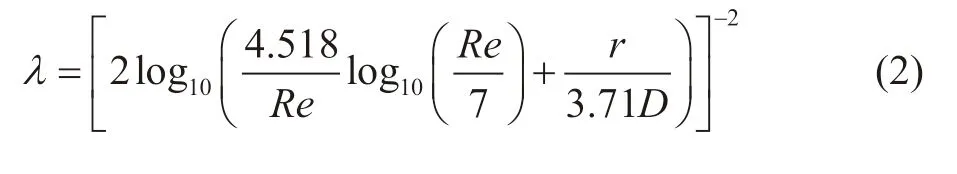
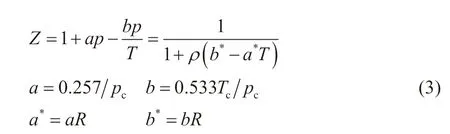
式中：Re为输气管道的雷诺数；r为管壁的绝对当量粗糙度，m；pc气体的临界压力，Pa；Tc气体的临界温度，K。

管段的传递函数则是在方程组(1)的基础上推导得到，是关于上游的压力、流量和下游的压力、流量的频域表达式。对管段的动力学方程线性化并进行拉普拉斯变换获得频域上的常微分方程组。假定管道的进口压力和出口流量被指定为边界条件，可获得高阶的传递函数表达式。但通过这种方式获得的传递函数很难求得时域解析解，因此需要采用泰勒展开得到简化的传递函数表达式。

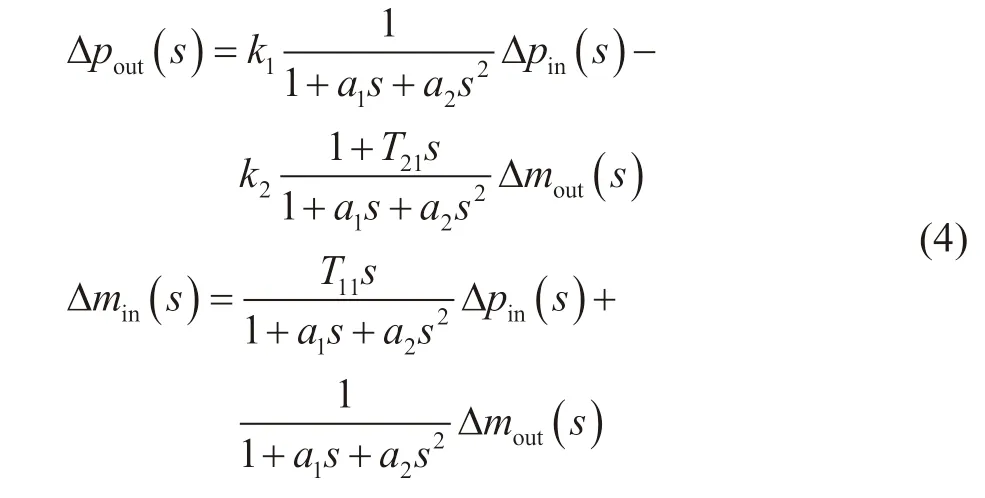
式中：

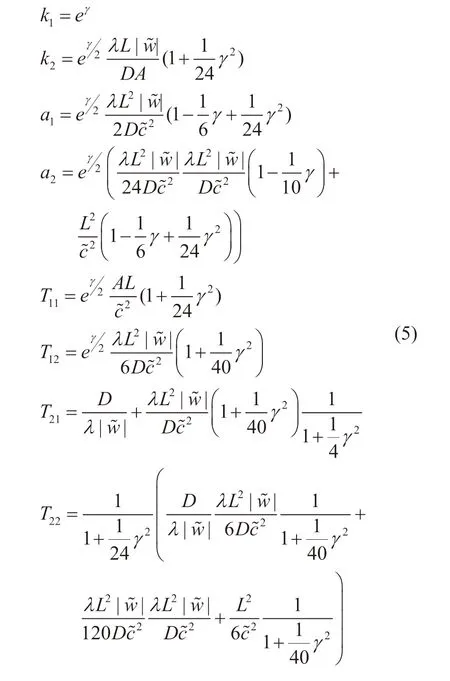
状态空间模型表达式如下

3 状态空间模型的适用性分析

状态空间模型是一个集总参数模型，即将一整段管道作为一个对象进行建模和分析。由于管道的分布参数特性，当我们将管道简化为某一点的状态集合进行分析时，管道的长度将对模型的精度和适用性产生直接影响。根据状态空间模型表达式(6)、(7)，编程实现模型参数的计算。

管道基础参数设定为：管道管径为1016 mm，粗糙度为0.04 mm，管道整体绝热，进口规定压力为10 MPa，出口规定流量为131 m³/s。管段按30、40、60、80、100、120、140、160、200 km共9种长度情况进行分析，对于不同的管道长度分别代入方程进行参数计算。

我们首先根据上述参数在SPS中搭建对应的仿真模型，进口规定压力为10 MPa，出口规定流量为131 m³/s，模型如图1。

在上文中推导的状态空间模型的基础上，根据管道对应状态参数和状态方程系数矩阵，计算得到描述管道系统特性的对应状态空间模型的参数。在MATLAB-Simulink中建立管道的可视化模型，包括描述管段特性的状态空间模型模块以及对应连接的输入输出模块。将计算得到状态空间模型的参数矩阵输入到对应的状态空间模块中，状态空间模型的输入是管段的进口压力和出口流量，输出是进口流量和出口压力。建立的Simulink模型如图2所示。

在分析中，我们对两种输入变化展开研究：一种是输入的进口压力产生阶跃扰动(0.2 MPa)而出口流量不变，而另一种是压力、流量都产生阶跃扰动(压力0.2 MPa、流量4 m³/s)。在这两种情况下，分别修改管段为30、40、60、80、100、120、140、160、200 km共9种长度进行分析。

图1 SPS模型Fig. 1 SPS model

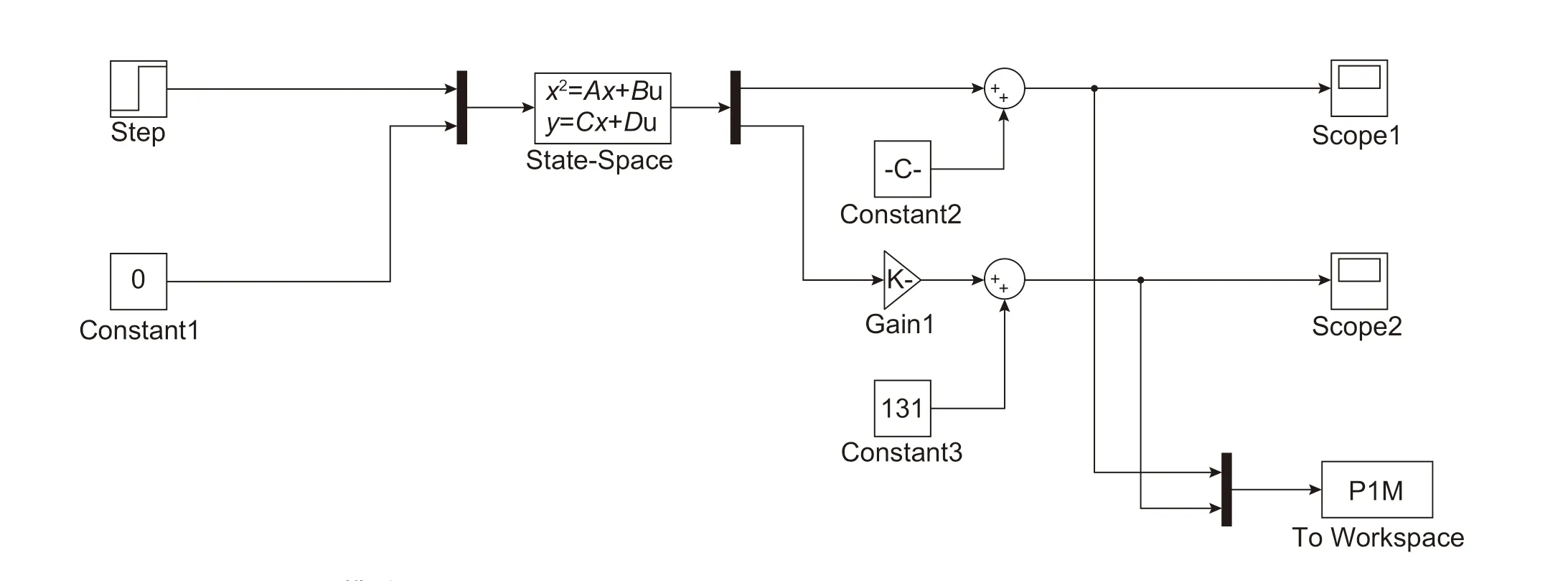
图2 MATLAB-Simulink模型Fig. 2 Matlab-simulink model

3.1 输入变化为压力阶跃

当输入信号的变化只有压力阶跃时，不同管段长度下的仿真对比结果如下所述。

从图3-1和图3-2中可以明显看出由于管段长度增加导致的稳定时间增加，同时模型与SPS的仿真结果之间的偏差也在增大。由仿真结果可知，当输入出现扰动时，输出的入口流量和出口压力值也随之产生变化。对于入口流量，无论管段长度如何，其输出流量都会在扰动出现的时间点瞬时增加。由于出口流量不变，输出的流量值也会逐渐趋于稳定值，即设定的流量值。对于出口压力，在扰动出现后，输出的压力也会随之变化，然后达到新的稳态值。

对于只有压力变化的情况，在100 km以上长度的管道，流量经历短期的波动后，最后都会回到原来的稳定值。这说明状态空间模型在流量的关系上可以达到与SPS模型相同的结果。图3-1(a)和图3-2(a)可以看到状态空间模型结果会出现振荡，这是由于管道长度过短时，管道本身的压力波传播特性占主要因素，会表现出一定的波动。在实际管道中由于摩阻和气体传热特性，并不会出现较大的波动。因此，状态空间模型并不适用分段长度过小的情况。由图3-1(c)和图3-2(c)可以看出对于过大的管段分段情形，状态空间模型的代数特性使它表现出与SPS模型在反应时间上较大的偏差。图3-1(b)和图3-2(b)反映了状态空间模型的仿真结果与SPS的仿真结果较为符合。其中100 km长管段条件下振荡完全消失，且在仿真反应时间偏差较小的情况下与SPS仿真结果较为接近。因此，对于管径为1016的气体管道，将其切分为100 km左右长度的管段采用状态空间模型进行分析比较合理。

3.2 输入扰动为压力和流量同时存在

当输入的变化既有压力阶跃，又有流量阶跃(4 m³/s)时，不同管段长度下的仿真结果如下所述。

在压力和流量同时出现阶跃扰动的情况下，我们可以得到与单独存在压力扰动情况下相同的结论。

由图3-1(a)、图3-2(a)、图4-1(a)和图4-2(a)中发现无论输入是否存在流量阶跃扰动，当管道长度较小时，模型仿真都会存在振荡现象。由3-1(b)、图3-2(b)、图4-1(b)和图4-2(b)可以发现振荡现象直到管道长度增加到80 km时才消失。理论上，随着管段的增长，模型的精度会逐渐降低。而在本算例中，由于振荡的存在导致在管段长度较小时，精度不是很高；当振荡消失时由于长度较大，精度也不是很高。状态空间模型是由传递函数模型变形得到的，使用这类模型进行仿真时，当管段长度足够小时均会出现振荡现象。随着管段长度的增加，振荡则会消失。管径越大，振荡现象消失时对应的管段长度越长。

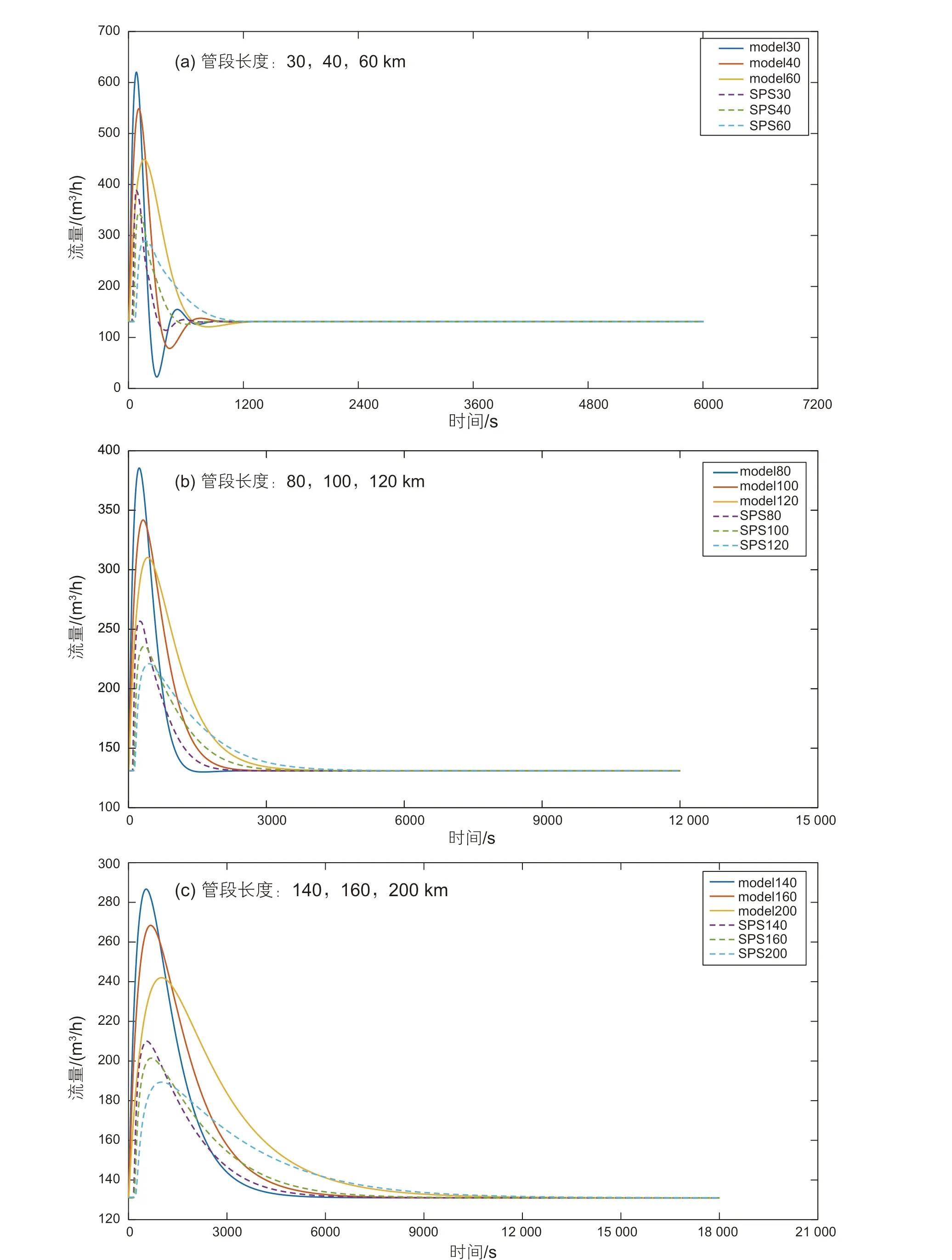
图3-1 只有压力阶跃时，不同管道长度下的输出流量对比Fig. 3-1 Comparison of output flow with different pipeline length

图3-2 只有压力阶跃时，不同管道长度下的输出压力对比Fig. 3-2 Comparison of output pressure with different pipeline length

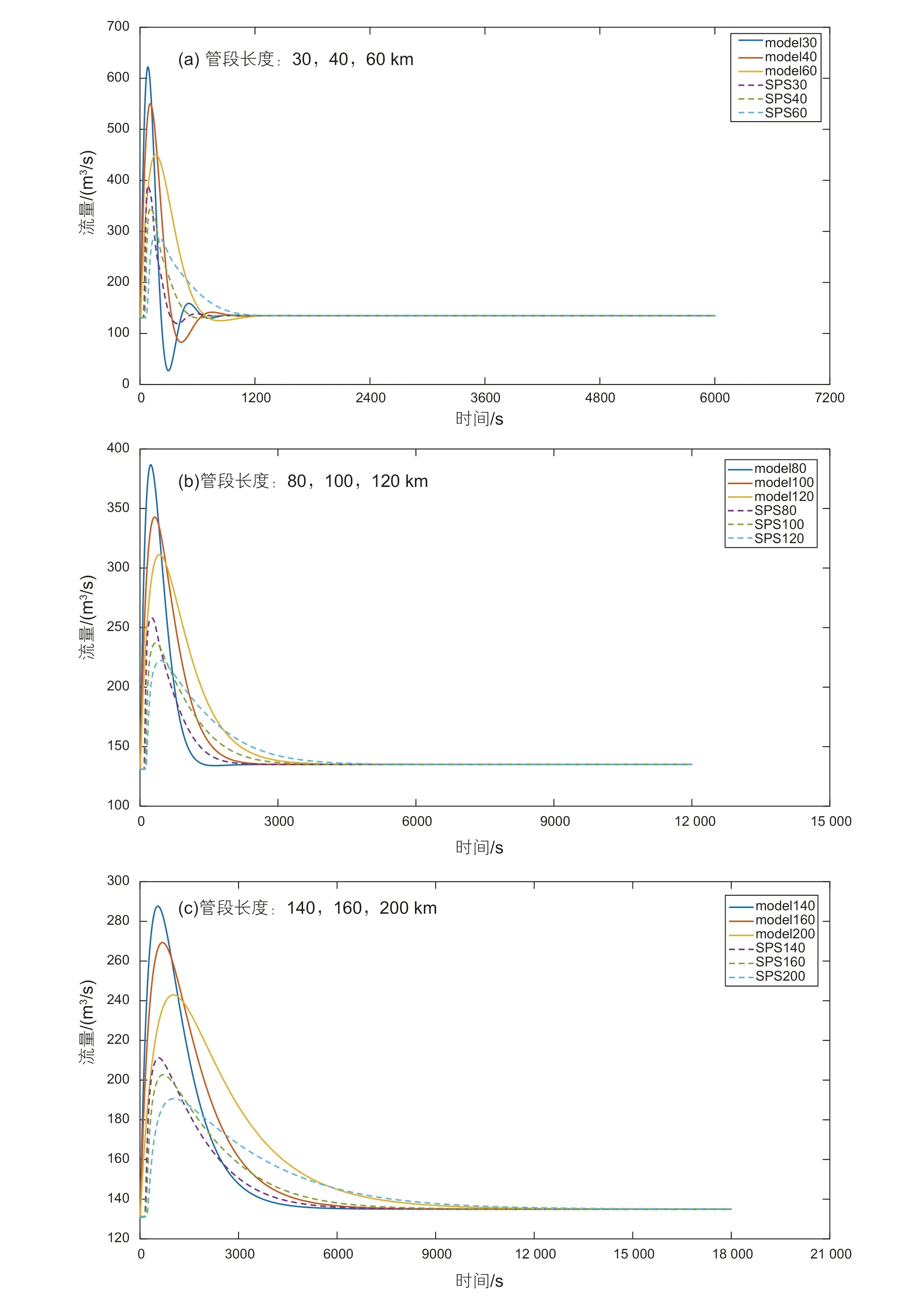
图4-1 即有压力阶跃，又有流量阶跃时，不同管道长度下的输出流量对比Fig. 4-1 Comparison of output flow with different pipeline length

由图3-1(c)、图3-2(c)、图4-1(c)和图4-2(c)可以发现，管道长度较长时，状态空间模型仿真稳定时间较长且与SPS仿真结果会有较大偏差。管段状态空间模型在一阶条件下其实是把管段作为存储可压缩气体的圆筒看待。当管段较短时，模型特性无法得到满足，则会出现振荡现象，而当管段长度较长时，一阶模型并不能良好的描述系统，会出现较大的偏差。故而对于管径为1016的天然气管道，状态空间模型的适用范围为80～120 km长管段，其中以100 km为最佳。

通过本算例我们发现状态空间模型可以简化天然气管道系统的建模，在不影响仿真精度的同时，减少了建模所需的管段数量。由于能够兼顾计算效率和精度需求，该模型适合于管道的动态控制。

4 状态空间模型鲁棒性分析

在由传递函数得到状态空间方程的过程中，我们用稳态线性化得到状态空间模型用于系统控制特性的分析。如果模型对于稳态点的选取过于敏感，则在此条件下做出的分析也只是针对特定的工况点而失去实际意义。因此，我们将分析不同工况点得到状态空间模型的差异性，从而说明状态空间模型是否能准确描述管道在各个工况点的动态特性。

在对连续性方程和运动方程进行线性化处理时，不同的稳态可以得到不同的传递函数。对于长度为60 km直径为1016 mm的天然气管道，在稳态流量 为55 m³/s、70 m³/s、85 m³/s、100 m³/s、115 m³/s、130 m³/s和进口压力为7.6 MPa、8.0 MPa、8.4 MPa、8.8 MPa条件下采用Bode分析展开结果。

线性管段模型的不确定性主要来源于一些参数值取进出口的平均近似结果以及参数由于运行点的改变而发生变化。图5-1～5-4对不同输入输出组合下的状态空间模型的鲁棒性进行了分析，流量越小阻尼比越小、谐振峰值的幅值越大，进口压力越大阻尼比越小、谐振峰值的幅值越大，谐振峰值的大小决定着时间响应振荡的强弱。对于1016管径管道，建立的状态空间模型在不同流量点线性化得到的幅频响应均没有出现较大的偏移，模型自身的稳定特性较好。这说明状态空间模型在描述天然气管道时，对于管道不同工况点具有良好的一致性。

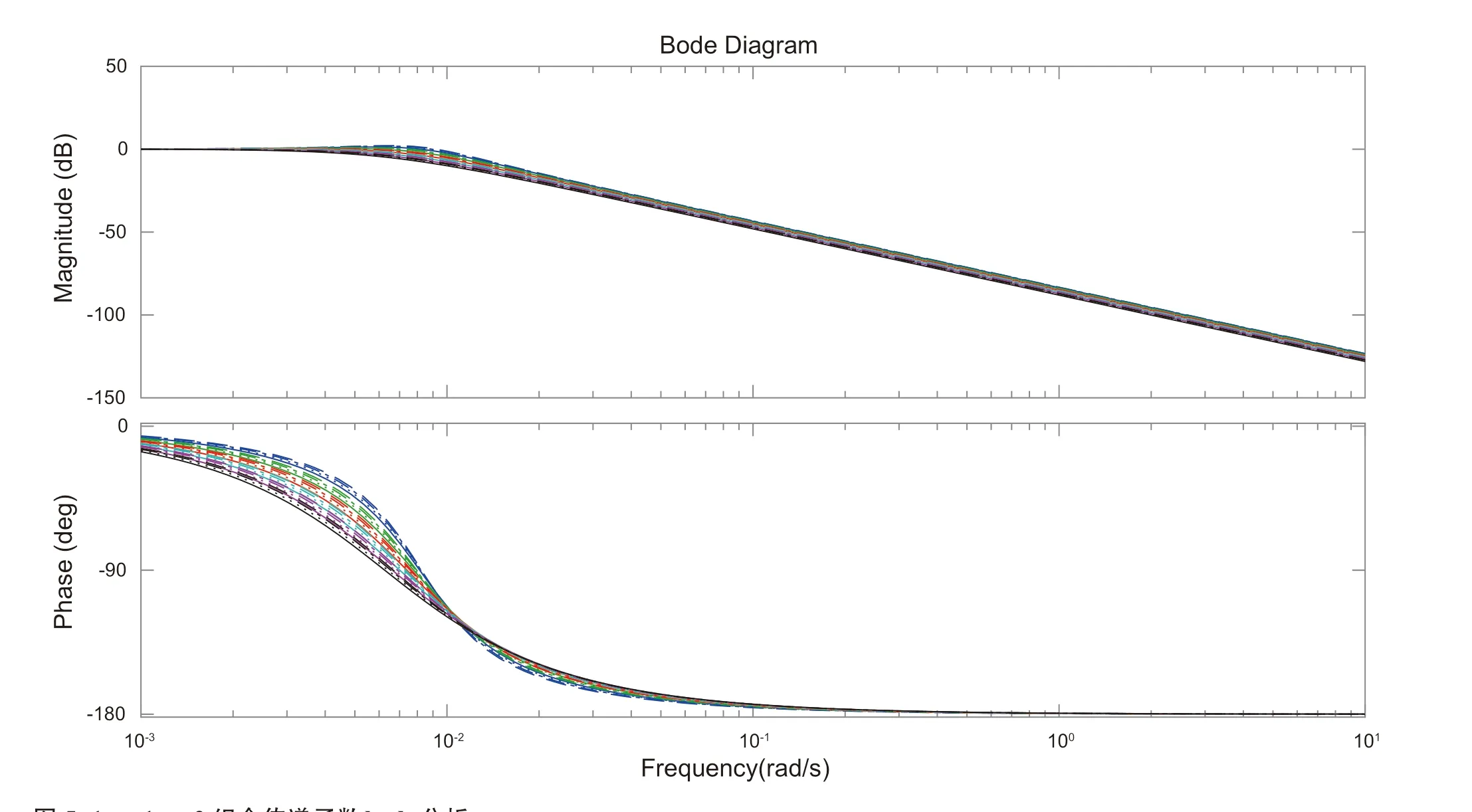
图5-1 p1、p2组合传递函数bode分析Fig. 5-1 Bode analysis of p1 and p2 combined transfer function

为了验证模型的鲁棒性还需要对模型在单压力变化和单流量变化下的稳定性进行分析，其bode图如图6-1和图6-2所示。

图5-2 m2、p2组合传递函数bode分析Fig. 5-2 Bode analysis of m2 and p2 combined transfer function

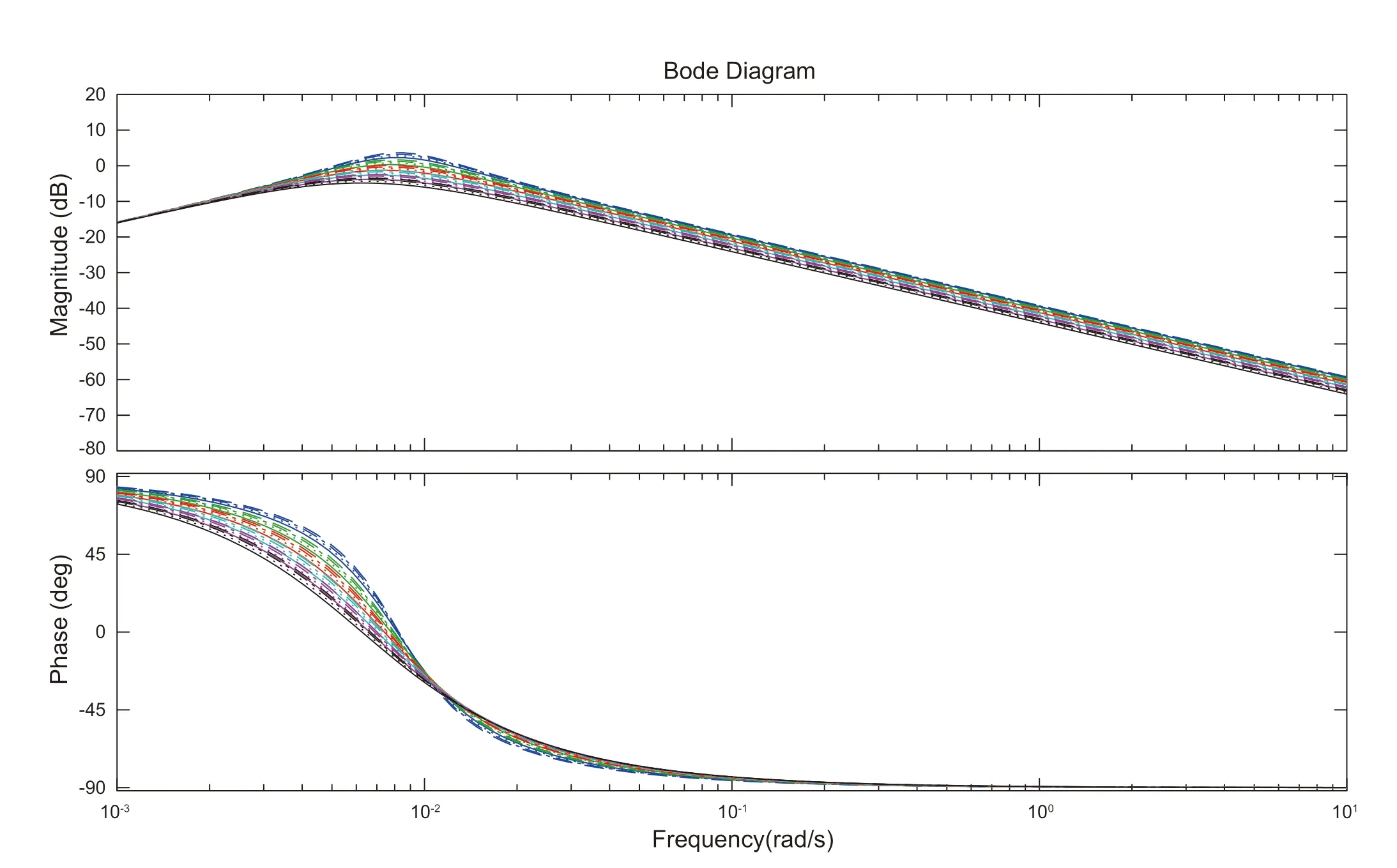
图5-3 p1、m1组合传递函数bode分析Fig. 5-3 Bode analysis of p1 and m1 combined transfer function

图5-4 m2、m1组合传递函数bode分析Fig. 5-4 Bode analysis of m2 and m1 combined transfer function

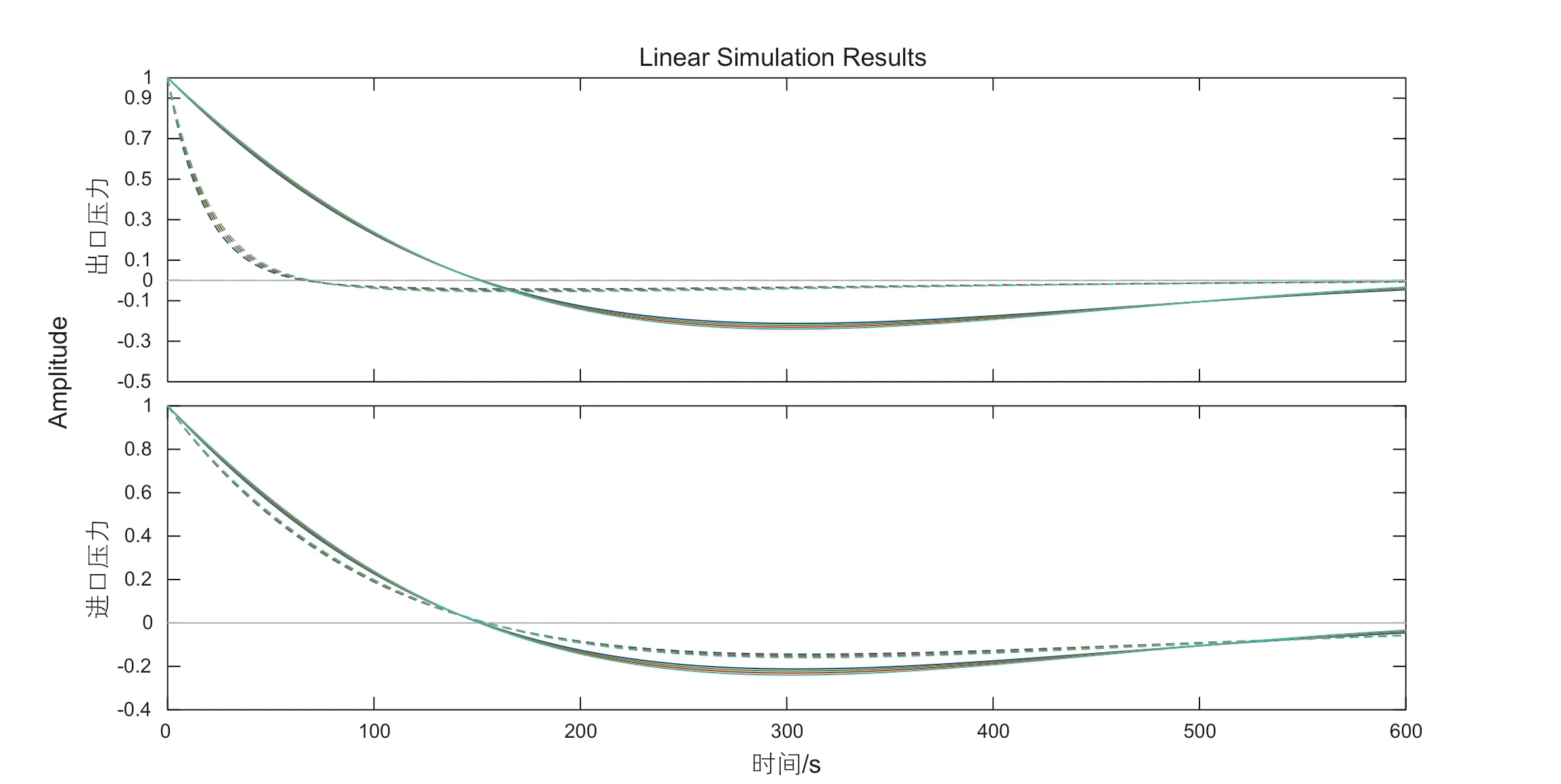
图6-1 流量在标称状态附近变化Fig. 6-1 Flow changes under standard state

图6-1和图6-2为分别选取稳态流量为100 m³/s和进口压力8.0 MPa为标称状态。图6-1中假定稳态流量不变，稳态进口压力为7.2 MPa、7.6 MPa、8.0 MPa、8.4 MPa、8.8 MPa；而 在 图6-2中 假 定稳态进口压力不变，稳态流量为70 m³/s、85 m³/s、100 m³/s、115 m³/s、130 m³/s。当压力、流量分别发生改变时，系统的频率特性并无较大偏移，状态空间模型的动态性能仍然非常接近。因此，我们认为状态空间模型在描述适用长度的管段时具有较强的鲁棒性。

图6-2 压力在标称状态附近变化Fig. 6-2 Pressure changes under standard state

5 结论

状态方程作为控制理论中常用的建模方法，能够将管道系统简化为状态量、输入和输出3个模块，兼顾计算精度和计算效率。选取管段长度是建模时需要考虑的重要因素，选取管段长度过短，会导致整体模型模块过多，建模复杂；而长度过长时则会导致模型失真。本文对不同管段长度和工况点的模型准确性进行了分析，结果可以分为3大类：第1类建模管段长度过短，模型振荡严重；第2类长度适中，仿真结果良好；第3类长度过长，模型失真。对于只关注管道进出口压力、流量的情况下，大口径天然气管道可以用状态空间方程分段近似分析。该模型可以将管道的分段扩大到100 km左右，这对于提高计算速度和进一步综合系统整体信息有很大的作用。状态空间模型对于工况点邻域内的波动不是非常敏感，具有很好的动态扩展性。状态空间模型能够描述管道本身的非线性、大时滞等特点，在此基础上可以采用经典控制方法进行控制器的设计。

(责任编辑 王雨墨 编辑 马桂霞)