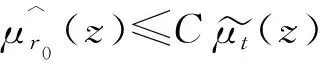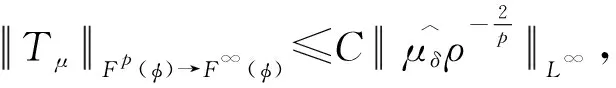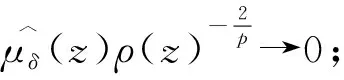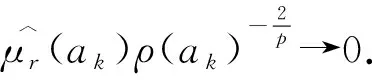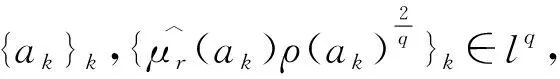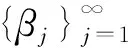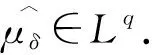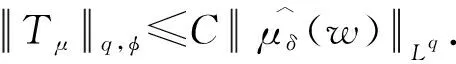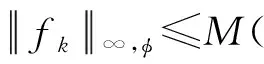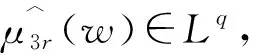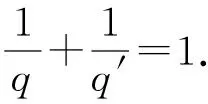Doubling Fock空间之间的正Toeplitz算子
2020-04-01简舒曼王晓峰
简舒曼, 王晓峰, 夏 锦
(广州大学数学与信息科学学院,广州 510006)
1 引 言
记C为复平面.令D(z,r)={w∈C:|w-z|
μ(D(z,2r))≤Cμ(D(z,r)),
r>0,称μ为doubling测度,其中z∈C.
设dA为C上的Lebesgue面积测度,φ次调和、实值且不恒为0,μ=ΔφdA为doubling测度.则对任意z∈C,总存在函数ρ(z)使得μ(D(z,ρ(z)))=1.称ρ(z)为正半径.函数ρ-2可看做是φ的正规化.
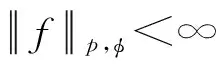

设H(C)为C上的全体整函数,加权Fock空间Fp(φ)定义为
Fp(φ)=Lp(φ)∩H(C).


令K(·,·)为F2(φ)的Bergman核,即对于f∈F2(φ),
若μ为C的Borel测度,合测度μ符号的Toeplitz算子定义为
对经典Fock空间上Toeplitz算子,已有很多结果, 如文献[6].当μ>0时,Isralowitz和Zhu[7]刻画了经典Fock空间上正测度符号Toeplitz算子Tμ的有界性和紧性,其中测度μ满足
Schuster与Varolin[8]利用均值函数与t-Berezin变换刻画了广义Fock空间上Toeplitz算子Tμ的有界性和紧性及其充要条件.Hu等人[9]利用Fock-Carleson测度刻画了广义Fock空间Fp(φ)与Fq(φ)之间的Toeplitz算子的有界性与紧性,其中0 在文献[13]中,Hu和Lv讨论了加权doubling Fock空间Fp(φ)与Fq(φ)之间的以正测度符号的Toeplitz算子的有界性与紧性的充要条件,其中0 在证明本文结果前,先介绍一些记号.对两个量A和B,AB表示存在无关紧要的常数C使得A≤CB,A≃B表示AB和BA同时成立. 其中Dr(z)=D(z,rρ(z)),r>0,z∈C.对于p>0,z∈C,Fp(φ)中的正规化Bergman核定义为 给定t>0,设μ的t-Berezin变换定义为 引理2.1[13]加权Fock空间Fp(φ)满足如下性质: (i) 给定p,t>0,实数k,存在C>0使得 其中z∈C; (ii) 对于0 其中z∈C; (iv) 存在与z,w无关的常数ε,C,z,w∈C使得 (v) 存在常数r0使得 其中z∈C,w∈Dr0(z). 引理2.2[13]设0 其中z∈C, 引理2.3[13]设0 引理2.4[13]设{ak}k为一个r-格.对于0 证明 由文献[13],当0 命题真. 引理2.6[13]设0 (i)Tμ:Fp(φ)→Fq(φ)有界; 引理2.7[13]设0 (i)Tμ:Fp(φ)→Fq(φ)紧; 引理2.8[13]设0 (i)Tμ:Fp(φ)→Fq(φ)有界; (ii)Tμ:Fp(φ)→Fq(φ)紧; 定理3.1设0 (i)Tμ:Fp(φ)→F∞(φ)有界; 证明 由引理2.3,(iii)⟹(iv)成立,且 由引理2.6知 (iv)⟹(ii)成立. 则 定理3.2设0 (i)Tμ:Fp(φ)→F∞(φ)紧; 证明 由定理3.1,(iii)⟹(iv)和(ii)⟹(iii)显然成立.由引理2.7可知(iv)⟹(ii)成立. (i)⟹(ii).设Tμ:Fp(φ)→F∞(φ)紧.由引理2.1(v)知{kp,z:z∈C}在Fp(φ)有界,且在任意紧子集上一致收敛于0.则 定理3.3设0 (i)Tμ:F∞(φ)→Fq(φ)有界; (ii)Tμ:F∞(φ)→Fq(φ)紧; 证明 由定理3.1,(iii)⟺(iv)⟺(v),(ii)⟹(i)成立.下证(i)⟹(v),(iv)⟹(i)及(iv)⟹(ii). (i)⟹(v).对任意一r-格{ak}k,{λk}k∈l∞,令 由引理2.4, 则 由Khinchine不等式和Tμ的有界性有 另一方面,由{ak}k的r-格性质知 则

2 预备知识


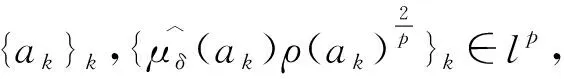

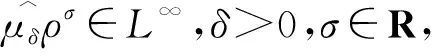

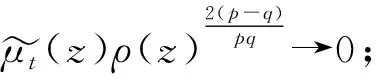

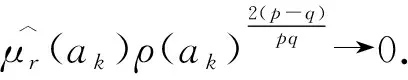

3 具有正测度符号的Toeplitz算子