局部遮阴下光伏阵列的最大功率点追踪策略
2020-04-01王传捷谷廷坤
王传捷, 谷廷坤, 吴 昊
(1.山东大学 电气工程学院,山东 济南 250061;2.国家电网济南市电力公司,山东 济南 250001)
0 引 言
由于石油、煤炭等各种化石能源的日益枯竭,以及环境问题的日益严重,新能源的开发迫在眉睫,而具有清洁优点且取之不尽、用之不竭的太阳能发电正受到越来越多的关注[1]。但是由于太阳能电池的输出特性呈现出非线性特点,以及光伏发电过于依赖光照等因素,导致发电效率低下、且太阳能电池只能够在某一特定的电压处达到其全局最大功率点,故需要进行最大功率追踪(Maximum Power Point Tracking,MPPT),使得负载的输出功率能达到一个最大值,从而提高利用率[2-5]。
通过对太阳能电池输出特性的分析与研究,可以计算出太阳能电池在最大功率点附近的电压近似值[6-7]。扰动观察法是一种传统的最大功率点追踪方法,它最大的优点就是控制概念清晰、被测参数较少,通过一些简单的判断及运算即可追踪到最大功率点[8-10]。但是这种方法在局部遮阴情况下容易陷入局域最大功率点,造成误判,甚至振荡无法稳定,同时造成一定的功率损失。因此如何利用扰动观察法追寻局部遮阴下光伏阵列的最大功率点,需要进一步地深入研究。
本文通过分析太阳能电池输出特性并结合扰动观察法,提出了一种新的最大功率追踪策略。首先对局部遮阴下光伏阵列的输出特性进行分析,测量在特定电压处电流的大小,分析出最大功率点的大体位置,再利用本文提出的改进扰动观察法进行最大功率点追踪,从而追踪到全局最大功率点。
1 在局部遮阴下光伏阵列的输出特性
1.1 光伏阵列建模
单个太阳能电池等效电路如图1所示。
太阳能电池的输出电流-电压特性方程为
(1)
式中:Ipv——单个太阳能电池的输出电流;
Iph——太阳能电池的光生电流;
Io——等效反向饱和电流;
q——电荷量,约1.6×10-19C;
Upv——单个太阳能电池的输出电压;
Rs——太阳能电池的串联电阻;
A——二极管理想系数;
k——玻尔兹曼常数,约1.38×10-23J/K;
T——温度;
Rp——太阳能电池的并联电阻。
式(1)虽然能够较好地体现太阳能电池内部组件对其输出特性的影响,但是由于太阳能电池的外部特性有很强的非线性,且Iph、IO、A等参数难以测量,因此工程上一般不使用该模型。
本文基于太阳能电池在标准测试条件下(温度TSTC=25℃、光照强度SSTC=1 000 W/m2)的4个参数(短路电流Isc、开路电压Uoc、最大功率点电压Ump0、最大功率点电流Imp0)进行工程数学建模。
通常情况下,太阳能电池的串联电阻Rs很小,且并联电阻Rp很大,因此可以忽略Rs和Rp对太阳能电池建模的影响。故式(1)可以简化为[11]
(2)
(3)
(4)
单个太阳能电池的输出电压为
(5)
对于单个太阳能电池的电流,可以表示为[12]
(6)
式中:Ipv,STC——标准测试条件下单个太阳能电池的输出电流;
KI——电流系数;
ΔT——太阳能电池的温度变化量;
S——太阳能电池接收到的光照强度。
由于太阳能电池的串联电阻Rs很小,故Ipv≈Isc,则式(6)可以近似为
(7)
式中:Isc,STC——标准测试条件下单个太阳能电池的短路电流。
根据以上太阳能电池的工程数学模型,在MATLAB/Simulink中搭建仿真模型。本文假设Ns个太阳能电池串联组成一个光伏串,并且Np个光伏串并联组成光伏阵列。根据式(5),同一个光伏串上电流相同的ns个太阳能电池的电压和为
(8)
1.2 光伏阵列的输出特性曲线
本文中所使用的是3×2的光伏阵列,局部遮阴情况A如图2所示,即由3个电池串联成光伏串,再使用两个光伏串进行并联组成光伏阵列,其中S1、S2、S3分别代表的光照强度为1 000、300、600 W/m2。光伏阵列的模型是基于上述工程数学模型搭建,所使用的太阳能电池参数如表1所示。

表1 太阳能电池参数
光伏阵列组件的输出特性曲线如图3所示。当一串太阳能电池有两种不同的光照强度时,会出现两个平台,每一个平台的电流值基本保持不变。当光伏阵列工作在电流较大的平台时,只有处于高光照强度下的太阳能电池会发出电流,而其他太阳能电池无电流发出,并且电流会流过它们的旁路二极管;当在电流较低的平台时,所有的太阳能电池均发出电流。根据图3,每个平台对应一个最大功率点,故寻找到平台的位置,即可大致确定最大功率点处的电压。
首先对第一个光伏串的输出特性曲线进行分析,当电流处于比较小的平台时,光伏串最左侧的电压为[13]
Us1s2,left=Us1,1+Us1,2
(9)
式中:Us1s2,left——第一个光伏串中第二个平台最左侧的电压值;
Us1,1——第一个光伏串处于高光照强度时电池的电压;
Us1,2——第一个光伏串处于低光照强度时电池的电压。
根据上述分析,光伏阵列在该电压值下工作时,只有处于高光照强度下的光伏电池会发出电流,且电流流过其他光伏电池的旁路二极管(旁路二极管反向饱和电压为-0.8 V),故
Us1,2=-1.6 V
(10)
同时,根据式(7)计算出第二个平台处电流的大小,若G=300 W/m2,ΔT=0,则
Is1s2=1.245 A
(11)
式中:Is1s2——第二个平台处的电流。
将式(11)代入式(8)中,计算出此时光伏串光照强度较高部分的电压值,即
Us1,1=32.46 V
(12)
将式(10)和式(12)代入式(9),得
Us1s2,left=30.86 V
(13)
此时,得出在第一个光伏串中,第二个平台最左侧的电压值接近Uoc。
与第一个光伏串类似,将数据代入计算第一个光伏串所使用的公式中,可以得到:
Us2s2,left=61.6 V
(14)
式中:Us2s2,left——第二个光伏串中第二个平台最左侧的电压值。
同时也可以得出在第二个光伏串中,第二个平台最左侧的电压值接近2Uoc。
综合上述分析,两个光伏串的输出特性曲线的特征基本相同,在一定条件下的电流基本是恒定值,同时第二个平台最左侧的电压值近似等于整数倍的开路电压,又由于光伏阵列是由两个光伏串相加组成的,故与光伏串有相同的平台特性。
2 最大功率追踪方法
2.1 寻找最大功率点处的电压
所使用的最大功率点追踪方法的流程如图4所示。当光伏阵列处于均匀光照强度时,使用扰动观察法追踪全局最大功率点,且随时判断功率的变化量ΔP。若ΔP<ΔPcrit(ΔPcirt最早在文献[14]中提出,本文中ΔPcrit=0.05Pmpp,其中Pmpp为最大功率点处的功率),则光伏阵列工作在均匀光照下,没有局部遮阴出现;若ΔP≥ΔPcirt,则光伏阵列的工作环境发生变化,即局部遮阴出现,此时需要进行全局最大功率点追踪。通过上述分析可知,在每一个平台最左侧,即最小的电压值都是单个太阳能电池开路电压的整数倍,同时每一个平台的电流值基本不变,故通过测量整数倍单个太阳能电池开路电压处的电流值,将其进行比较计算,即可计算出I-U特性曲线中平台的数量,从而得到光伏阵列最大功率点的数量。
通过式(15)判断aUoc与(a+1)Uoc是否在一个平台上,其中本文a取值为0、1、2。
(15)
式中:Ia——光伏阵列在电压aUoc处的电流值;
ΔItest——比较量。
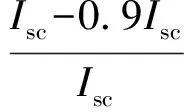
2.2 改进的扰动观察法
与传统的扰动观察法相比,本文提出的改进的扰动观察法可以更加精确地追踪在特定电压范围内的局域最大功率点[15-19]。
根据上述方法计算得到m×0.8Uoc,在P-U曲线上以U=m×0.8Uoc为对称轴建立一个开口向下的二次函数曲线。改进的扰动观察法中的二次函数曲线如图5所示。在建立的二次函数上使用扰动观察法追踪,在接近光伏阵列最大功率点电压m×0.8Uoc处,即|Utrk-m×0.8Uoc| 本文所使用的控制电路为Boost电路,通过控制Boost电路的占空比进行最大功率追踪,系统原理如图7所示。光伏阵列接入Boost电路的输入端,输出端是负载电阻,Boost电路参数如表2所示。在MATLAB/Simulink中搭建模型进行仿真实验。 表2 Boost电路参数 在0~0.3 s,光伏阵列处于均匀光照下,使用扰动观察法进行最大功率追踪;在0.3~1.6 s,局部遮阴情况A出现;在1.6~1.9 s,局部遮阴情况B出现;1.9 s以后,局部遮阴情况C出现。局部遮阴情况B和C如图8所示,S4、S5、S6分别代表的光照强度为400、700、500 W/m2。在均匀光照及局部遮阴情况B和C下,光伏阵列的输出特性曲线分别如图9~图11所示。 光照连续改变时光伏阵列的输出功率及输出电压如图12所示。在0.3 s,局部遮阴情况A出现,最初使用的P&O方法会失效,光伏阵列陷入局部最优,从0.35 s开始进行全局最大功率点追踪。测量0.6Uoc、Uoc以及2Uoc处电流的大小,分别为8.16、5.39、3.73 A,由式(15)得(8.16-5.39)/8.16>0.1、(5.39-3.73)/5.39>0.1,得到光伏阵列的3个最大功率点处的电压约为26、53、80 V;在1.6 s,局部遮阴情况B出现,计算可知有3个最大功率点,电压约为26、53、80 V;在1.9 s,局部遮阴情况C出现,此时有两个最大功率点,电压约为26和80 V。在这些点分别使用改进的扰动观察法进行追踪并比较,即可追踪到各个局部遮阴情况下光伏阵列的最大功率点。 在0~0.3 s,光伏阵列处于均匀光照下,使用扰动观察法进行最大功率追踪,输出功率稳定在615 W,而此时光伏阵列的最大功率为625 W,准确性可以达到98.4%;在0.3 s,局部遮阴情况A出现,输出功率有较大的变化,从0.35 s开始进行全局最大功率点追踪,最终稳定的最大功率为300 W,而此时光伏阵列的最大功率为305 W,准确性可达98.4%;在1.6 s,局部遮阴情况B出现,稳定的最大功率为378W,此时光伏阵列的最大功率为381 W,准确性可达99.2%;在2.9 s,局部遮阴情况C出现,稳定的最大功率为326 W,而这种情况下光伏阵列的最大功率点在328 W,准确性可以达到99%。因此文中所提的方法有较强的可行性。 分别使用本文中提出的方法以及文献[14]中的方法对局部遮阴情况A下的光伏阵列进行最大功率点追踪,并从追踪速度和准确度方面进行对比。 测量0.6Uoc、Uoc以及2Uoc处电流的大小,分别为8.16、5.39、3.73 A,由(8.16-5.39)/8.16>0.1、(5.39-3.73)/5.39>0.1得到光伏阵列共有3个最大功率点,对应电压值分别为26、53、80 V,在这3个点附近使用改进的扰动观察法进行追踪,即可得到全局最大功率点。 本文提出的方法和文献[14]中的方法最大功率点追踪结果分别如图13、图14所示。本文提出的方法在1.4 s时可以稳定在全局最大功率点处,约为300 W,此时光伏阵列的最大功率点处的功率为305 W,准确性可达98.4%;使用文献[14]提出的方法,约1.55 s时可以稳定在最大功率点处,功率为297 W,准确性可以达到97.4%。故本文所提出的方法无论在追踪速度上、准确度方面均比文献[14]提出的方法更加完善。 本文构建了光伏电池的工程数学模型,并对光伏电池的输出特性曲线进行了详细分析,利用最大功率点电压同开路电压之间的关系,计算局部遮阴下光伏阵列几个最大功率点处电压的近似值。使用本文提出的改进的扰动观察法进行追踪,即可追踪到全局最大功率点。通过MATLAB/Simulink搭建模型进行了仿真验证,并同文献[14]提出的方法进行了对比,分析得到以下结论: (1)在光照发生突变情况下,本文中提出的方法能够准确地判断出光照发生了突变,并能准确追踪到光伏阵列的全局最大功率点。 (2)与文献[14]提出的方法相比,本文中提出的方法在追踪速度以及准确度方面都有一定程度的提升。3 仿真验证
3.1 仿真电路及参数
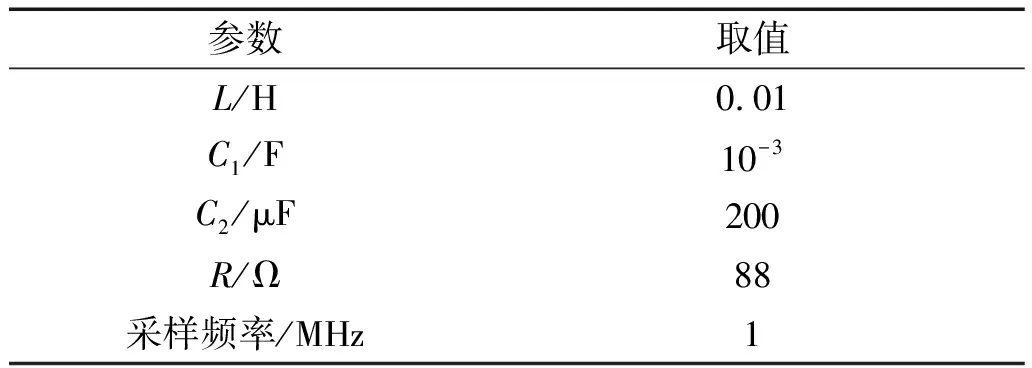
3.2 在连续不同的光照下进行最大功率追踪
3.3 与其他方法进行对比
4 结 语
