基于水平缝影响的蓄水期面板应力变形研究
2020-03-31王开拓罗永全雷双超王银涛
王开拓,罗永全,雷双超,王银涛
(1.青海民族大学 土木与交通工程学院,西宁 810007; 2.青海省水利水电(集团)有限责任公司,西宁 810000; 3.遵义水利水电勘测设计研究院,贵州 遵义 563000)
0 引 言
基于现代筑坝技术的发展,我国混凝土面板堆石坝建造自1985年后处于飞速发展状态,也就此累积了丰富的建筑经验。根据中国混凝土水电工程学会混凝土面板堆石坝专业委员会的最新统计,截至2017年底,中国的混凝土板堆石坝总数超过440座,其中75座正在建设中,约有89座处于规划阶段。中国面板堆石坝的数量占世界混凝土面板堆石坝总数的一半以上,坝高、工程规模与技术难度均位居世界前列。
坝结构组成部分众多,其中之一即为混凝土面板,其同样属于坝面防渗机制的主体,下游坝体的水压绝大部分都来自于混凝土面板。坝高、混凝土力学性能、自身结构以及堆石变形、堆石性质、气候、地质环境、河谷形态等均会影响到混凝土板应力。所以极有必需提高面板施工乃至于设计的标准。近年来,诸多专家学者针对混凝土面板分缝及新型面板结构对面板应力变形影响分析进行了相关研究[1-5]。特别是受气候、施工等因素影响,面板不得不进行分期施工而设置水平分缝或出现水平裂缝,因此研究水平缝对面板应力变形影响分析十分必要。
1 工程概况
本文采用ANSYS有限元分析软件分析石头峡水电站混凝土面板的非线性变形,探讨蓄水期不同水平分缝对面板应力与变形的影响。石头峡混凝土面板堆石坝位于青海省大通河流域,地处青藏高原海北州门源县,气候条件恶劣,年内施工期短,该工程等别为Ⅱ等大(Ⅱ)型工程,坝顶高程为3 091.30 m,坝顶宽为10 m,最大坝高为114.5 m,上游坝坡为1∶1.4,下游坝坡为1∶1.3。大坝标准断面图见图1。
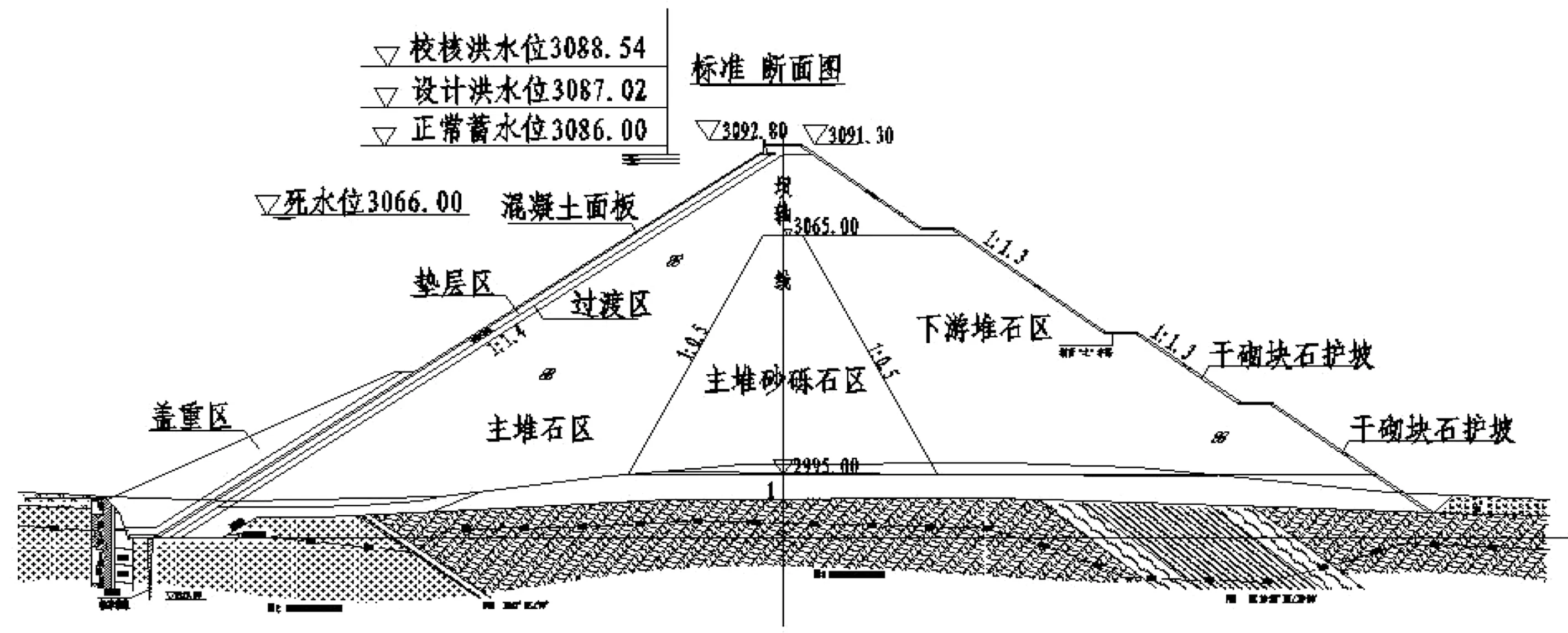
图1 大坝标准断面图Fig.1 Standard cross-section diagram of Dam
2 计算模型、参数及方案
2.1 计算模型
Goodman无厚度单元用于模拟假面板和底层之间的刚柔结合,水平分缝接触模拟则采用厚10~20 cm的薄层单元进行。水平缝的数量将根据不同计算方案的要求进行调整,以四边形单元及其退化单元为主进行网格划分,在不设置水平缝的基本模型中共剖分单元网格3 574个,结点10 978个,坝体单元2 876个。网格划分见图2。
2.2 计算参数
基于非线性弹性E-B模型求解堆石坝主堆砂砾石、主(次)堆石、垫层、过渡层。表1为各坝体材料求解参数。且采用C30混凝土材料模拟趾板、面板,采用线弹性模型模拟趾板、面板和基岩,泊松比0.167,弹性模量3×104MPa,施工缝表层(水平)设计成柔性止水结构,采用柔性填料[6],面板接缝材料弹性模量较低,该计算模型将面板接缝材料的等效弹性模量取为面板混凝土弹性模量的1/3。基岩泊松比0.2、弹性模量2.5×104MPa。各区材料参数详见表1。

图2 面板坝有限元网格Fig.2 Fine element meshes of CFRD

表1 各区材料参数统计结果Tab.1 District material parameters results
注:表中卸荷弹性模量数为Kur;体积模量指数为m;体积模量数为Kb;弹性模量指数为n;弹性模数为K;破坏比为Rf。
2.3 计算方案
为进行对比分析,按照坝体结构与模拟施工的情况[7],按照4种不同间距、2种不同缝体宽度的水平缝,建立6种不同的模型来研究水平分缝的数量和宽度对蓄水期面板的应力与变形的影响。具体方案如下:
模型1:无水平缝设置,因为是一次落成面板。
模型2:水平缝(1条)设于和坝体底相距61.6 m处,此处实质上也是坝体一期蓄水高度。设计厚20 cm薄层单元。
模型3:水平缝(1条)设于填筑3层坝体,从下到上水平缝设置距离间隔为1条/26.4 m,也就是说,将4条水平缝分别设于26.4,52.8,79.6和105.6 m高度部位,且采用厚20 cm薄层单元。
模型4:水平缝(1条)设于填筑两层坝体,从下到上水平缝设置距离间隔为1条/17.6 m,也就是说,将6条水平缝分别设于坝高17.6 m处、坝高35.2 m处、坝高52.8 m处、坝高70.4 m处、坝高88 m处、坝高105.6 m处,且采用厚20 cm薄层单元。
模型5:水平缝设于坝体各层填筑,从下到上水平缝设置距离间隔为1条/8.8 m,也就是说,将20条水平缝分别设于坝高8.8 m处、坝高17.6 m处、坝高26.4 m处、坝高35.2 m处、坝高44 m处、坝高52.8 m处、坝高61.6 m处、坝高70.4 m处、坝高79.2 m处、坝高88 m处、坝高96.8 m处、坝高105.6 m处。薄层单元的厚度取为20 cm。
模型6:水平缝设置的部位与总数与模型5一样,不过该模型采用的是厚10 cm薄层单元。
3 计算结果与分析
表2为各模型在正常蓄水期面板挠度与应力极值的分布情况。
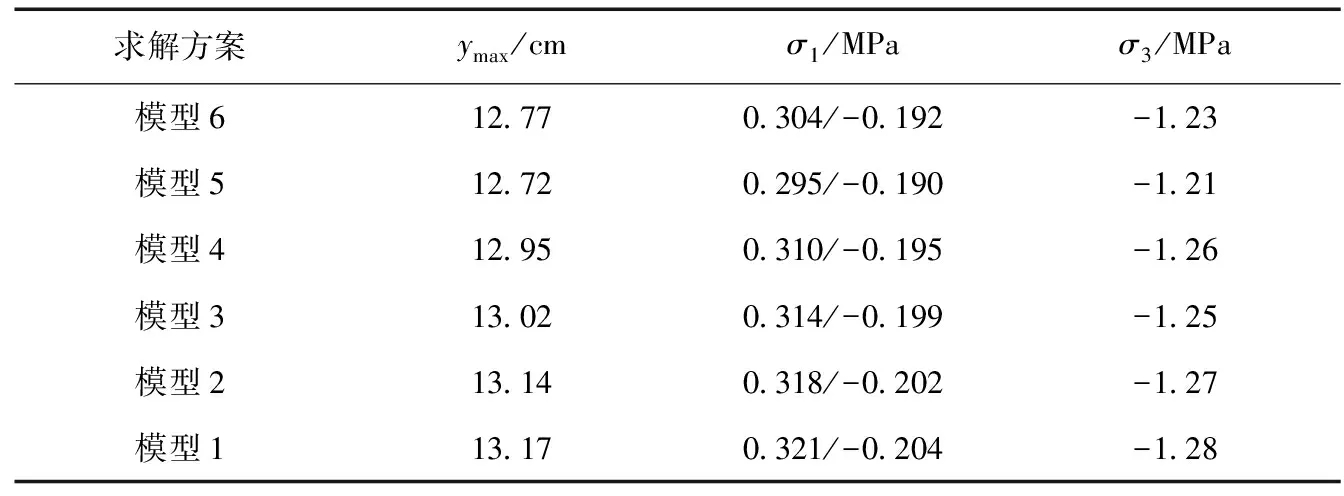
表2 应力极值和挠度分布Tab.2 The deflection and stress extreme value distribution
注:ymax表示最大法向挠度,σ1表示最大主应力,σ3表示最小主应力,“+”为压应力,“-”为拉应力。
3.1 挠度分析
通过以上6种模型计算结果的对比可以发现,面板挠度极少会受到水平缝宽度与数量干扰,所以本文只将无水平缝条件下面板挠度分布图(模型1)列出,图3即为两期面板交界部位周围面板最大挠度变形处,约处于1/2坝高处。从最大挠度点开始,挠度分布基本上向上侧、下侧持续变弱。模型1、模型4、模型5、模型6中的面板法向挠度最大值分别是13.17,12.95,12.72和12.77 cm,较模型5的变形稍大。基本变形规律大体上类似于坝体变形规律,堆石体荷载与沉降则决定面板变形程度。与此同时,最大法向挠度的发生部全基本无差异,用挠度变形最大为无水平缝模型,因为增加水平缝数量条件下会弱化薄层单元材料弹性模量,所以会增大面板挠度曲线的糙度,小折点会出现于水平缝周围,不过其影响总体上来看并不明显,最大差值为0.45 cm。
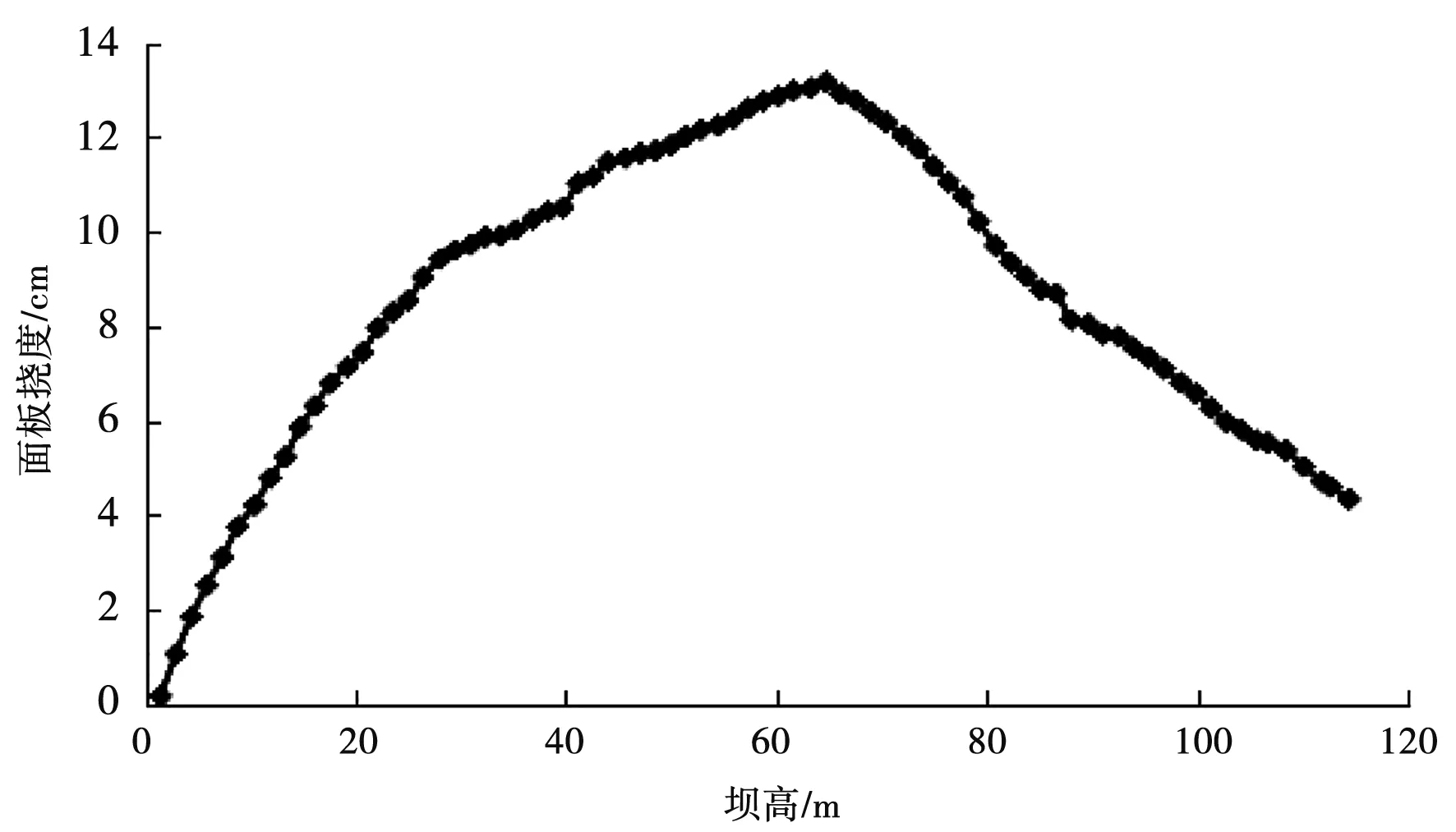
图3 面板挠度曲线图(不设水平缝)Fig.3 Deflection graph of faceplate(without horizontal seam)
3.2 应力分析
图4-图9为面板大主应力曲线,受拉区在面板的底部。在水压影响下,中间受压,且水压、面板压应力与高度均呈反相关,并表现出两头大、中间小现象,蓄水期面板大体处于受压状态也就此得到证实。1.21~1.28 MPa,0.295~0.321 MPa分别是6个模型的压应力、拉应力峰值。坝高7.33 m处为最大压应力值(6种模型均如此),而最大拉应力值发生处并不一样,模型1、模型2分别发生于51.37和49.93 m坝高部位,模型3、模型4出现在48.5 m处,模型5、模型6出现在49.93 m处,就此证实面板最大拉应力值与水平缝数量呈反相关关系,而且增加水平缝数量会在一定程度上降低最大拉应力值发生部位。模型1-模型6大主应力曲线图分别见图4-图9。
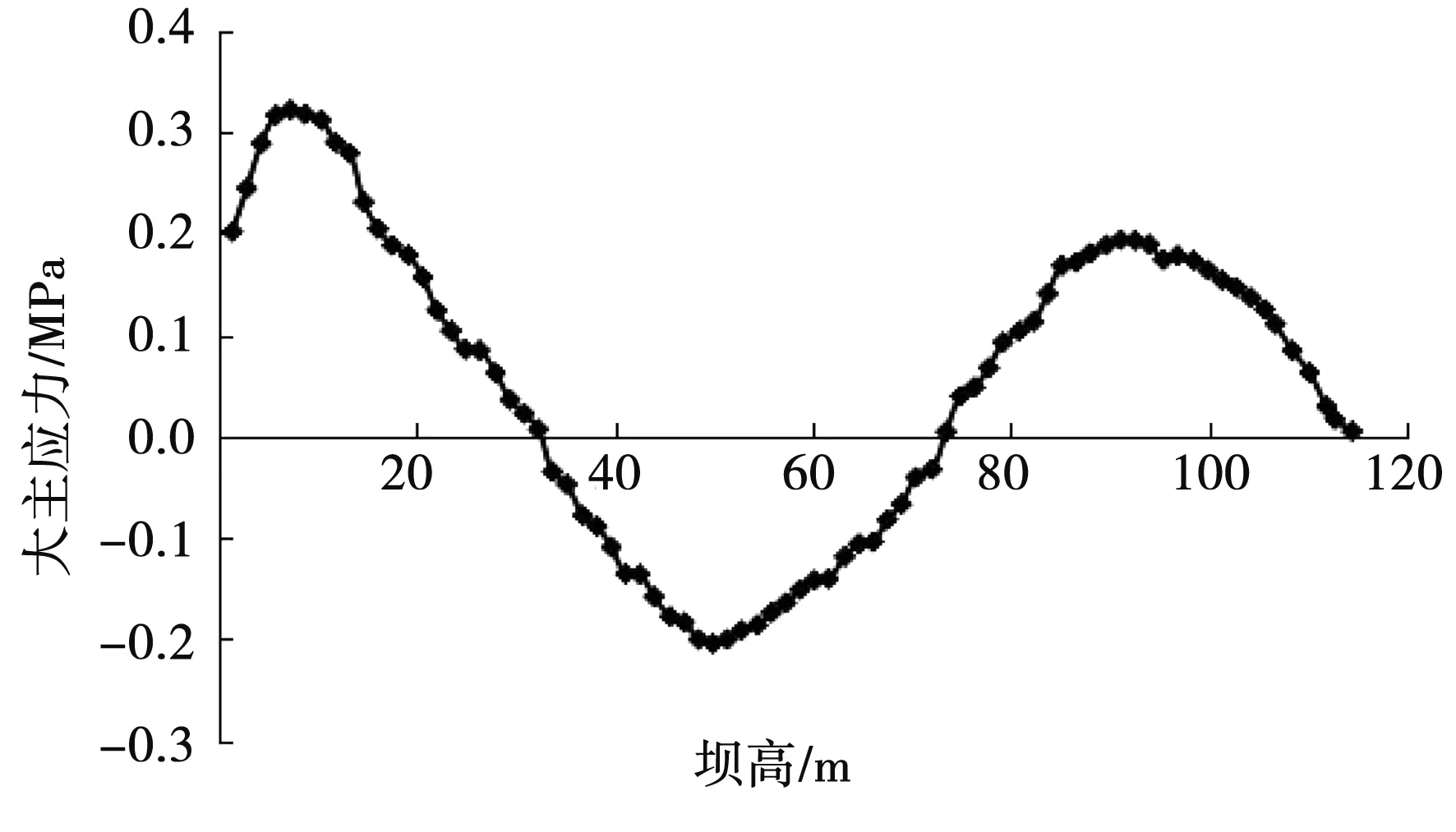
图4 大主应力曲线图(模型1)Fig.4 The major principal stress graph of model 1
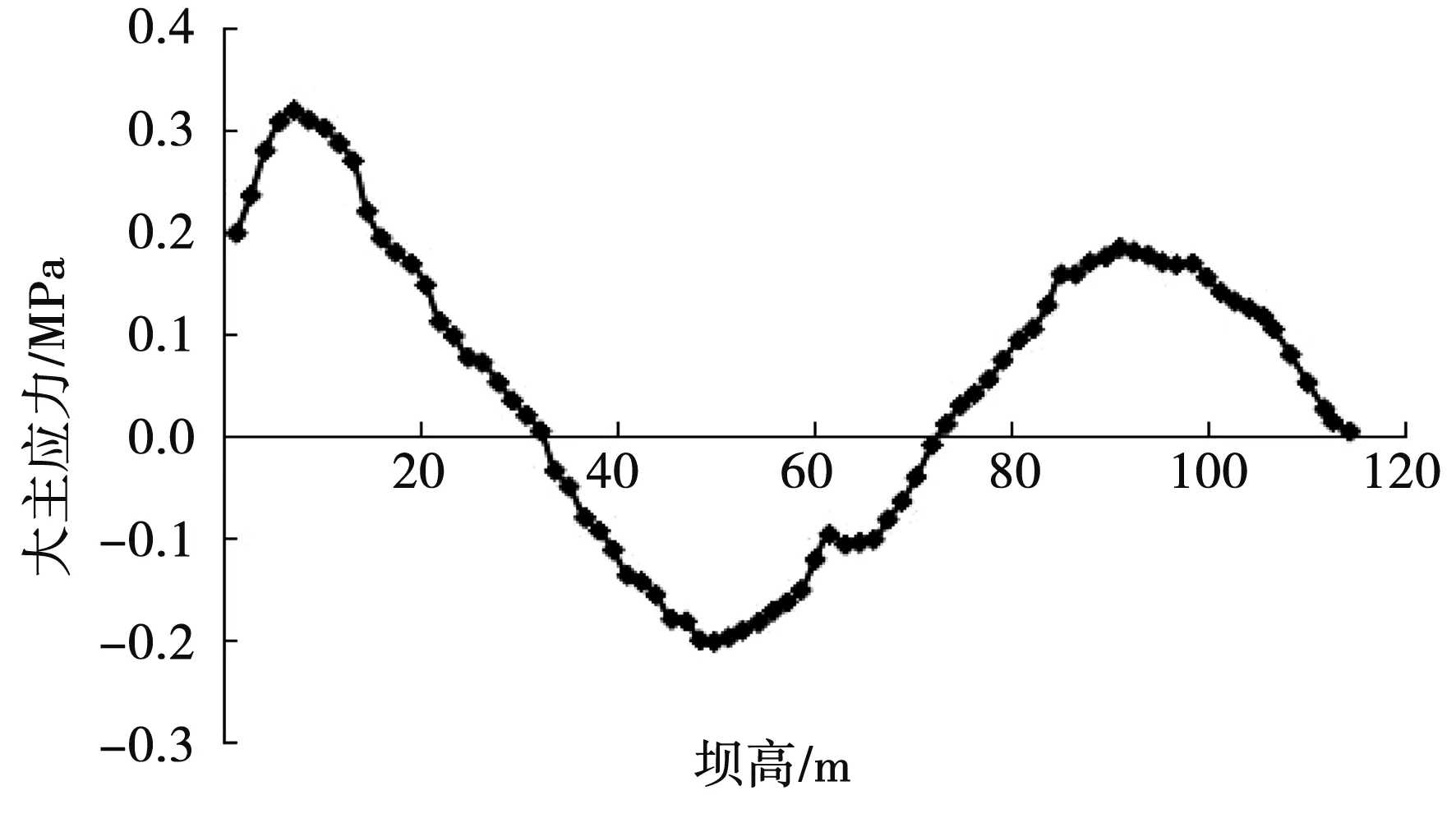
图5 大主应力曲线图(模型2)Fig.5 The major principal stress graph of model 2
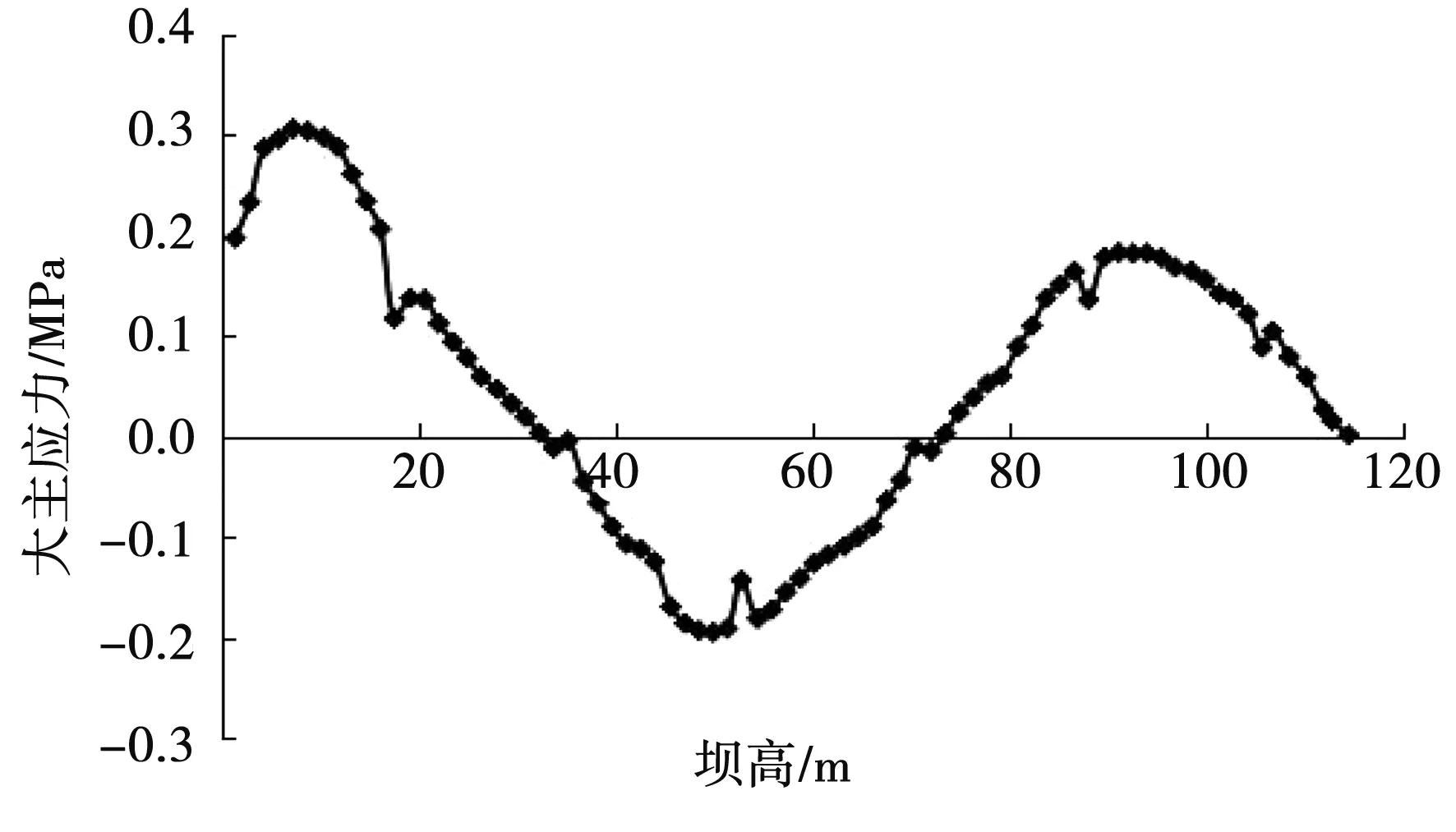
图6 大主应力曲线图(模型3)Fig.6 The major principal stress graph of model 3
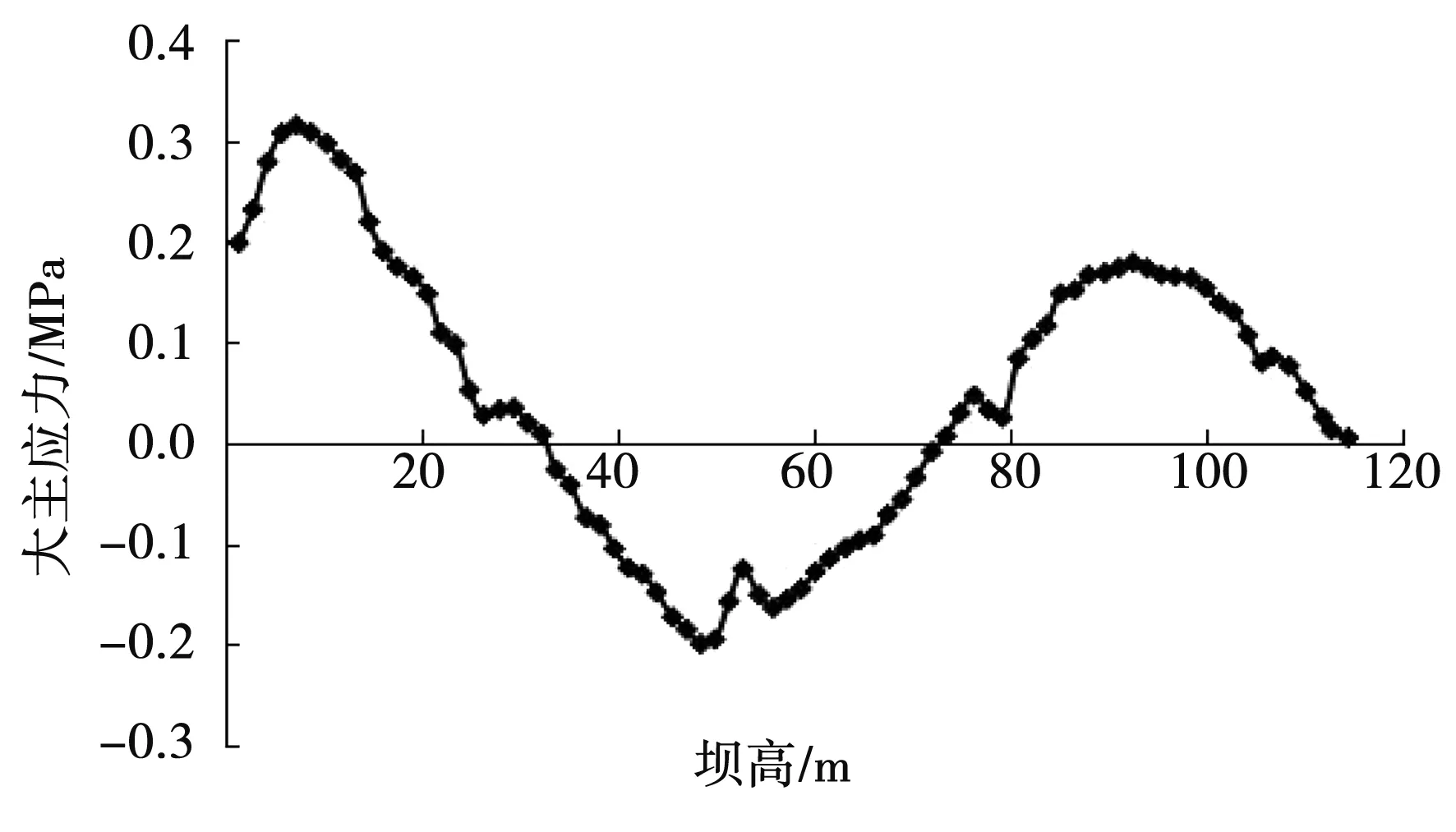
图7 大主应力曲线图(模型4)Fig.7 The major principal stress graph of model 4
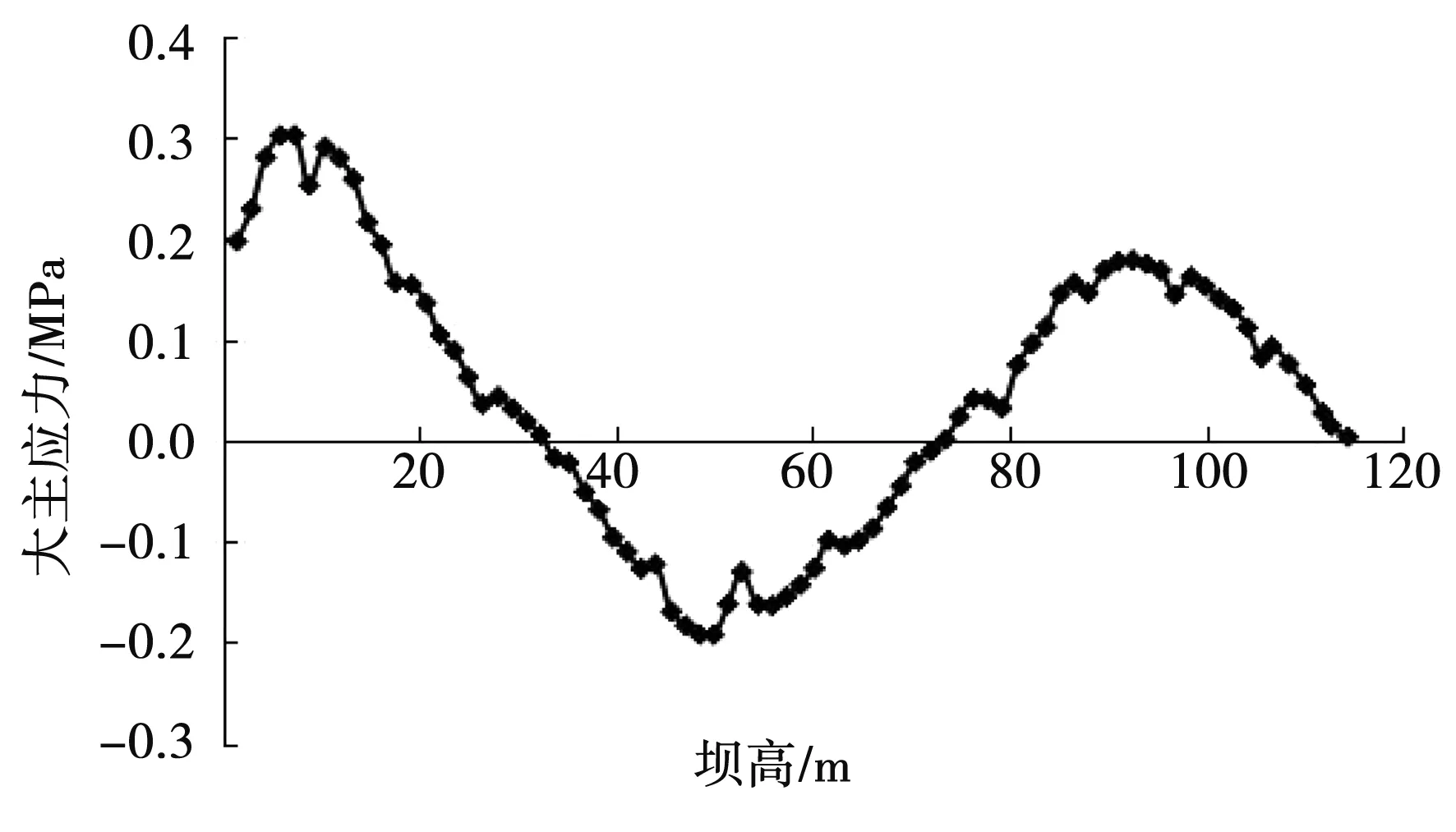
图8 大主应力曲线图(模型5)Fig.8 The major principal stress graph of model 5

图9 大主应力曲线图(模型6)Fig.9 The major principal stress graph of model 6
图10-图15分别为面板小主应力曲线。从中可以发现,面板应力主要表现出两头小、中间大现象,不过整体上依然保持受压状态,且坝高约1/3~1/2部位出现压应力值峰值。相对模型1中无水平缝情况,其余各模型水平分缝对应的位置处应力均有明显的减小折点。其中模型2中位于坝高61.6 m处的应力值由0.664 MPa下降至0.520 MPa,下降幅度为21.68%;模型3、模型4、模型5、模型6最大应力值均有所降低,下降幅度在约10%,最大压应力均出现在坝高41.43 m处。可见面板水平分缝数量的增加对最大应力所处的位置基本无影响。模型1-模型6小主应力曲线图分别见图10-图15。

图10 小主应力曲线图(模型1)Fig.10 The minor principal stress graph of model 1
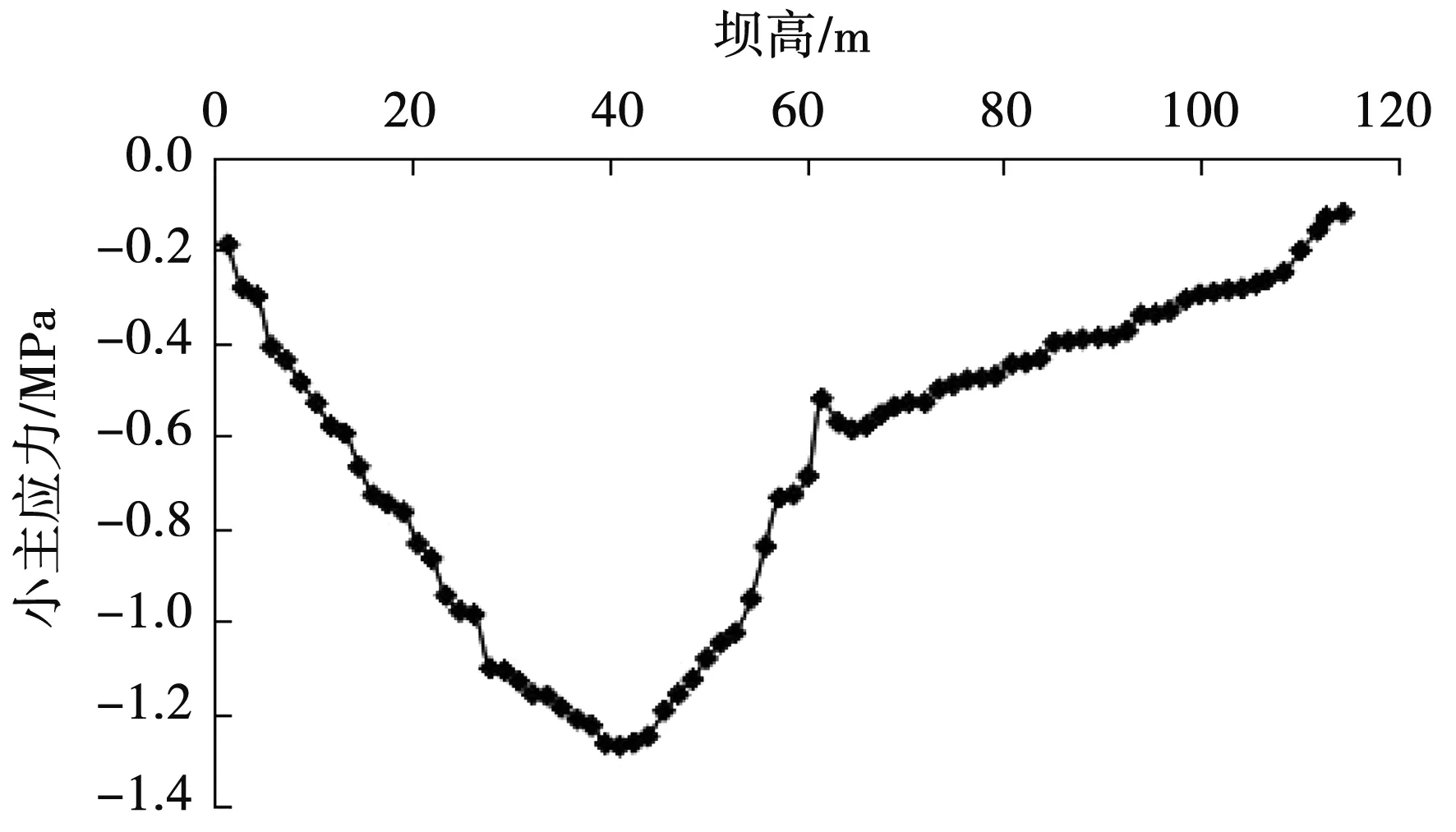
图11 小主应力曲线图(模型2)Fig.11 The minor principal stress graph of model 2
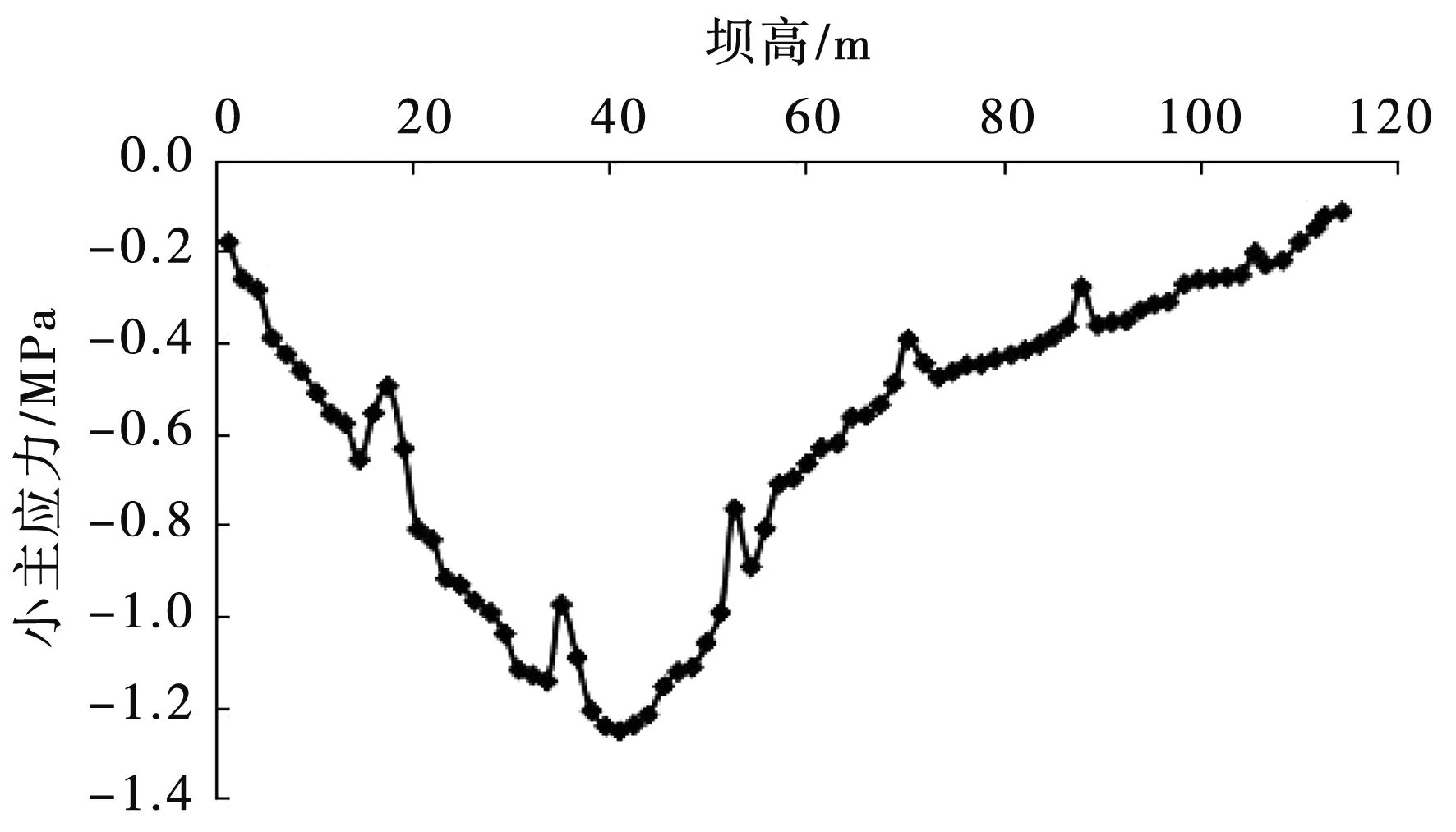
图12 小主应力曲线图(模型3)Fig.12 The minor principal stress graph of model 3

图13 小主应力曲线图(模型4)Fig.13 The minor principal stress graph of model 4
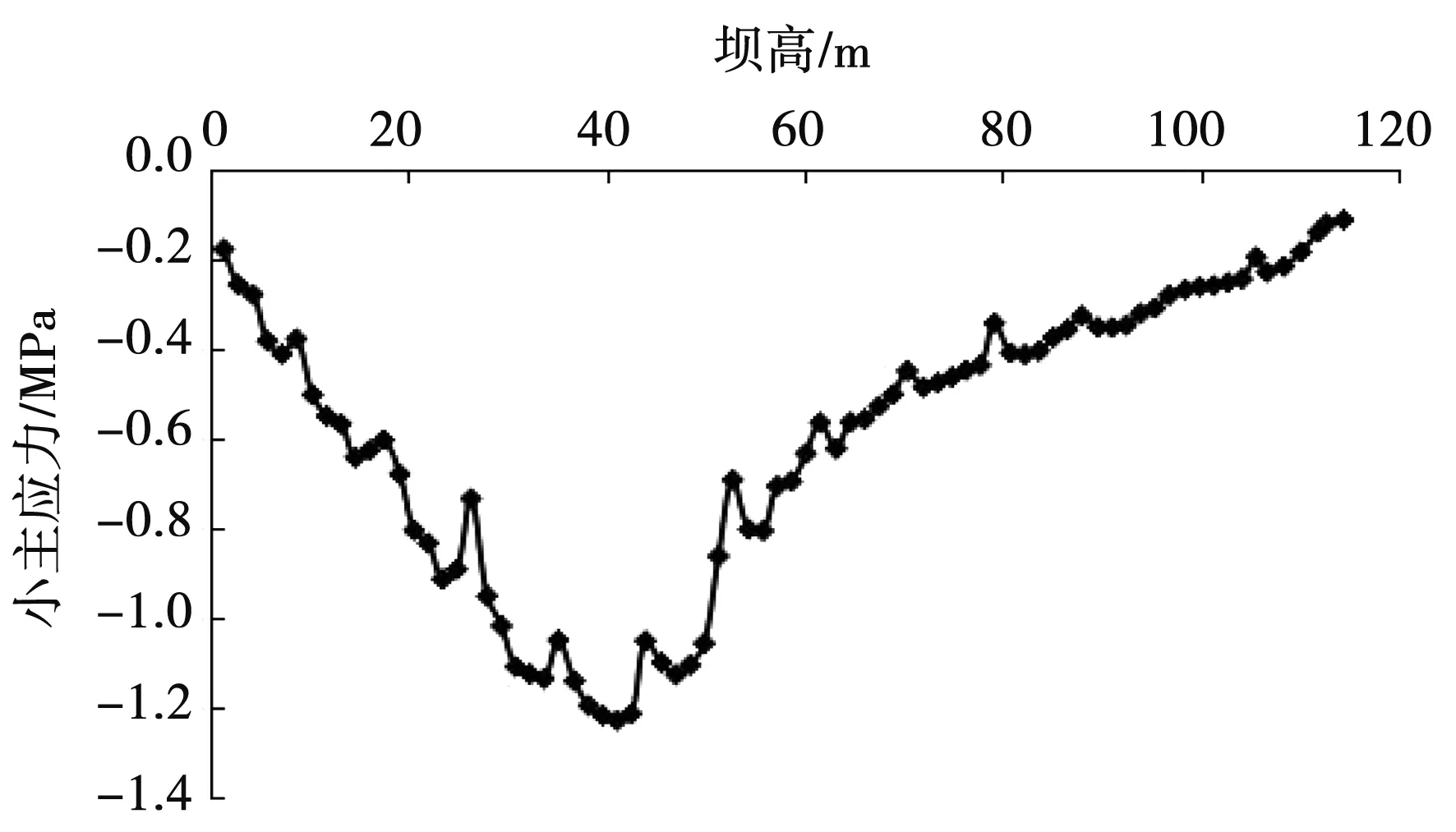
图14 小主应力曲线图(模型5)Fig.14 The minor principal stress graph of model 5
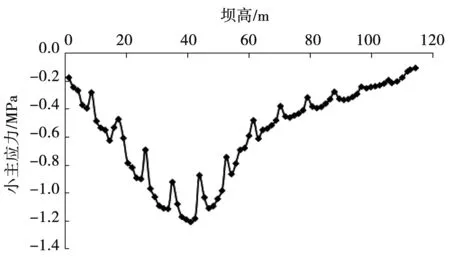
图15 小主应力曲线图(模型6)Fig.15 The minor principal stress graph of model 6
比较结果证实,面板压应力与水平分缝数量二者之间具有反相关关系,尤其在水平缝周围减小折点更加清晰,不过这并不会过多影响到总体应力的波动态势;面板压应力与水平分缝的宽度呈反相关,不过水平分缝的宽度不会显著影响面板压应力。因为水平分缝的宽度和数量增加几乎不会影响到面板拉应力与挠曲,所以通常将其忽略。
4 结 语
基于有限元分析方法,对比分析了蓄水期青海省石头峡水电站大坝面板在6种不同的水平分缝模型中的应力和挠度的影响及其分布规律,研究结论如下:
1) 坝体的应力变形大体上不会受到面板数及宽度的分缝这两种因素的干扰,坝体应力变形状态、坝体变形的程度均与同一级别且已竣工的类似工程应力变形规律吻合。
2) 设置更多水平缝时,能在一定程度上整体改善面板应力应变状态,尤其能够明显地弱化水平缝周围压应力,而拉应力与挠度也有减小趋势,但变化不大。
3) 面板的分缝数量不同,通常会程度不同的弱化面板压应力,特别是可以更明显地降低水平缝周围压应力,折点出现,缝宽的差异通常不会过多地影响到面板压应力。
4) 缝体的数量如果没有任何差异,那么增加面板水平缝的宽度通常是局部面板压应力下降的有利因素,而且这种情况不会过多地影响到面板挠度,所以通常将其直接忽略。
