江西省信江水坝安全性状评价分析研究
2020-03-31赵月
赵 月
(江西省水利水电建设有限公司,南昌 330200)
1 概 述
水坝作为我国水利工程中重要一项设施,水坝安全影响着水利工程的运行安全及能效发挥作用。水坝安全与否是决定水库后期维护策略方案的关键因素,如何及时快速准确地对水坝安全情况进行评价是水利工程运营维护人员最为关心的问题。
关于评价对象的安全性评价方法大致可以概括为以下6类:层次分析法、模糊评价法、集对分析法、神经网络分析法、可靠度理论分析法、物元可拓模型分析法[1-3]。每种方法各自拥有不同优缺点,物元可拓模型分析法作为新兴方法备受推崇,但它无法针对分段函数造成的指标之间不相容的缺陷作出很好的评价。因此对其合理改进,若能避免该情况的发生在理论上还是值得研究尝试。
本文以江西省上饶市余干县水电站为研究对象,对其安全性状进行评价。针对物元可拓模型的不足进行有利改进,并建立相应的评价指标体系与划分安全等级,计算各个指标的关联程度,最终得到综合关联度数值,对水坝运营安全安全等级对应,为后期运营维护提供理论依据与导向。
2 评价指标选择
为了能够比较全面准确地概括水坝安全性,充分结合相关规定[7],综合考虑评价指标的获取难易程度,建立评价指标体系。其中主要由工程质量评价、运行管理评价、防洪标准评价、结构安全评价、渗流安全评价、抗震安全评价、金属结构评价共7个一级安全评价指标。各一级安全评价指标依照实际情况细分成多个二级评价指标。具体评价指标体系及分级见图1。
3 评价模型建立
针对水坝安全性评价主要选择物元可扩模型进行评价。在该模型内,设定被评价对象为A,其特征用B表示,并且该特征数值为C。A,B,C这3个元素按照顺序构成三元组R=(A,B,C),该三元组是描述被评价对象的基本元,又称物元。换句话说,被评价对象的名称A、被评价对象的特征B、被评价对象特征数值C是构成物元R的3个基本要素。当物元R含有多个特征时,可以选择用向量方式表达B=(B1,B1,…,Bn)形成评价指标体系,与之对应的特征值选择向量C=(C1,C1,…,Cn),此时物元R是n维物元。物元可拓模型具有很多优势,尤其针对具有多种矛盾且各矛盾间不相容的评价对象尤为适用。结合评价指标体系建立的实际情况,利用物元可拓性与可拓集的关联函数从定性分析和定量计算两个方面依次完成对水坝安全性的评价工作。

图1 水坝安全评价指标体系
3.1 明确经典域Ro与节域物元Rp
根据被评价对象的特性与其对应的统一标准化数值范围构成的物元矩阵规定为经典域Ro;节域Rp主要是由经典物元、被评价对象、被评价对象的特征、被评价对象特征对应的数值范围4部分组成,每个部分不可缺少。两者的数学表达式如下:
Ro=(Po,B,C)=(Po,Bi,Ci)
Ci=[xi,yi]
(1)
Rp=(P,B,Cp)=(P,Bi,Cpi)
Cpi=[xpi,ypi]
(2)
式中:Bi(i=1,2,…,n)是被评价对象A若干个评价指标体系(表示其特征);Ci(i=1,2,…,n)为被评价对象A关于评价指标B对应的数值变化范围,即C=[x,y],其数值变化的上下限即为x,y;Cpi为被评价对象A关于评价指标B的数值变化范围,即Cpi=[xpi,ypi]。依据定义及数学知识,显然Ci⊂Cpi。
3.2 标定被评价对象物元矩阵
综合考虑被评价对象的特征选择与之对应的特征量数值Cei,构造被评价对象的物元矩阵Re,具体表达式如下:
Re=(Pe,B,ce)=(Pe,B,cei)
(3)
式中:cei为Pe与其评价指标Bi对应的实际数值,同理与对应的向量ce=(ce1,…,cen)为B=(B1,…,Bn)实际检测数值。
3.3 标定关联函数与关联度数值
本文设定距表示在实数轴的点c距离指定区间co=(x,y)的长度值。根据上述物元可拓模型描述,被评价对象A的评价指标Bi的实际测量数值为cei、经典域量值范围与节域量值范围,通过三者计算,得到距的计算公式如下:
(4)
式中:ρ(cei,Ci)为cei和Ci之间的长度,即距;同理ρ(cei,Cpi)为cei和Cpi之间的距。
依据高等数学知识,关联函数是指被评价单元与某一标准规定之间的隶属程度的函数关系式,其数值大小表明两者关联程度的高低,具体的关联程度函数关系表达式如下:
(5)
3.4 综合关联度数值计算
在计算出个评价指标的关联度值后,依照其重要程度赋予一定的权重因子,计算各关联度的加权和,计算公式如下:
(6)
式中:K(Pe)为准备评价单元Pe所对应的区间关联程度数值;wi为第i项评价指标给定的权重因子。
当Kj=max(K(Pe))(j=1,2,…,m),此时Pe等安全评价等级是j级。
4 模型改进
经典物元可拓模型计算出来的关联函数为分段函数,因为水坝安全性状评价指标区间长度均等、节域端点确定等因素,当利用经典关联函数公式获得各评价指标的关联度时,同一指标量值对应的评价区间位置一致时对应多个关联度数值,或者节域端点对应不同的评价等级时有可能出现关联程度数值一致的情况。对其关联程度计算公式结合实际评价情况进行改进,具体公式如下:
K(cei)=-ρ(cei,Ci)/|Ci|
(7)
当关联度数值大于零时,则量值处于该区间内,表明被评价对象达到标准对象的规定;当关联度数值小于零时,则此时量值在该区间之外,表明被评价对象未达到设定标准对象的规定;当关联度数值等于零时,此时量值在该区间的两端临界点。关联度数值的大小表示量值与该区间中间点的远近,数值越大,距离中间的越近,反之亦然。
5 指标权重分析

(8)

(9)
6 水坝分析
本文以江西省上饶市余干县信江水电站的水坝为研究对象,利用改进的物元可拓模型对该水坝的安全性进行评价。水库的枢纽建筑物主要有主坝、副坝、泄洪道、输水涵洞、坝后电站等,该水电站定位是以灌溉为主,防洪发电为辅,设计常年蓄水量为85.5×104m3。结合水坝实际运营情况,将水坝安全评价指标划分成5个安全等级:I(非常安全),II(安全),III(较为安全),IV(不安全),V(非常不安全),与之对应的评价指标规定范围依次是[0.75,1],[0.5,0.75],[0.3,0.5],[0.15,0.3],[0,0.15]。充分考虑该水利工程实际运转情况,给定各个评价指标数量值,具体见表1。

表1 各评价指标给定的标准数值
将结构安全评价指标作为具体案例,对其一级指标评价进行确定。重点明确其经典域、节域、被评价物元3个部分,具体见如下矩阵。

利用计算式(4)求出结构安全评价指标对于上述划分的5个安全等级各自的距,再利用式(7)依次计算得到每个评价指标的关联度数值,具体数据见表2。
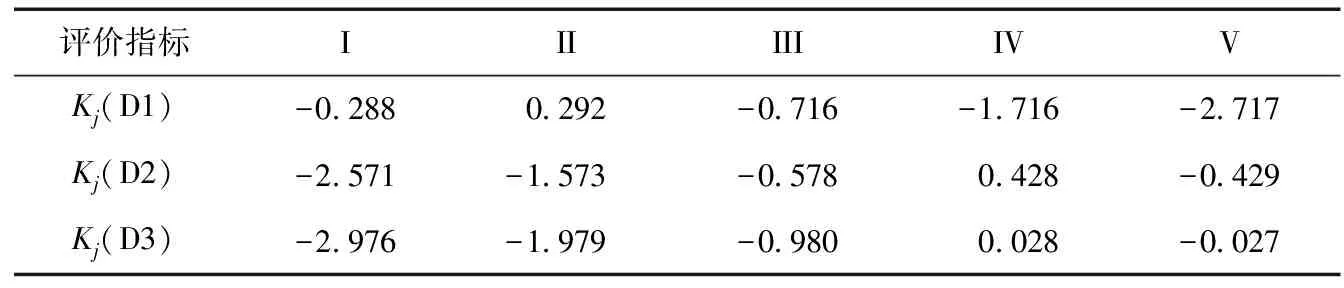
表2 所有指标对评价等级的关联度数值表

同理,与上述步骤一致,依次计算求出其它一级评价指标的综合关联程度数值,具体数据见表3。

表3 一级评价指标对应计算出的综合关联度数值

7 结 论
本文以江西省上饶市余干县信江水电站为研究对象,结合实际情况建立相应的评价指标体系并将安全等级划分为5个等级。改进物元可拓模型,计算各个指标的关联程度,利用熵权法给定权重因子数值,计算综合关联度数值,对水坝运营安全进行合理评价。评价结果显示,与实际运行情况相符,即证明改进物元可拓模型的适用性。水坝安全威胁主要是因为运行管理欠缺、金属结构存在安全隐患,为后期运营维护提供了思路导向。
