基于离差最大化的地铁车站踩踏风险评价

张亮亮 刘连珂 孙东冶

摘 要：为有效评估地铁车站发生拥挤踩踏事故风险的大小，文章建立基于离差最大化的地铁车站拥挤踩踏风险评价模型。首先，建立地铁车站拥挤踩踏事故风险的评价指标;其次，利用离差最大化方法研究地铁车站拥挤踩踏事故风险评价指标的权重，并以此为基础，建立地铁车站拥挤踩踏事故风险评价方法;最后，利用离差最大化模型对地铁车站实测的数据进行分析及评价，并得到各车站拥挤踩踏事故风险的大小及排序。研究结果表明：基于离差最大化方法能够充分利用客观信息对车站拥挤踩踏事故风险的大小进行分析及評估，该方法具有可行性和有效性。

关键词：地铁车站;踩踏事故;风险评价;离差最大化方法

中图分类号：U231+.92，X928.9

1 研究背景

由于客流量大、客流集中、人员密集等特点，地铁在运营生产过程中存在诸多安全隐患，特别是因乘客拥挤引起的踩踏安全隐患尤为突出[1]。地铁车站一旦发生拥挤踩踏事故，不仅会危及广大乘客的生命安全，还有可能影响地铁线路、网络的正常运转。为此，有效评估地铁车站拥挤踩踏事故风险的大小，有利于支持地铁运营单位制定预防拥挤踩踏事故发生的应急预案，提高地铁运营管理水平[2-3]。

目前，国内学者对地铁车站拥挤踩踏事故风险的评价指标体系及评价方法进行了一系列的研究。朱昌锋[4]利用信息熵方法提取了城市轨道交通运营安全评价指标，并利用数据包络分析（DEA）方法对城市轨道交通运营安全进行了评价;王志华[5]运用层次分析法确定各评价指标的权重，建立了以物元理论为基础的综合评价模型;王起全[6]从人、物、环境和管理4个方面入手，提出了导致地铁车站拥挤踩踏事故的原因;佟瑞鹏等[7]研究指出弱势人群比例等是地铁车站拥挤踩踏事故的触发因子;刘艳等[8]考虑输出向量权重限制问题，利用改进的DEA模型对地铁车站拥挤踩踏事故风险进行评价;角志达等[9]建立了地铁车站拥挤踩踏事故风险DEA评价模型;霍宇芒等[10]采用层次分析法和熵权法确定了评价指标的组合权重，并利用模糊物元评价模型评估地铁车站拥挤踩踏事故风险大小;尹晓庆[11]采用模糊故障树分析和模糊综合评价相结合的方法评估地铁站拥挤踩踏风险;于恒等[12]基于可拓理论，建立了地铁车站安全评价体系。

考虑到地铁车站踩踏风险评价属于多属性决策问题，而离差最大化方法是一种常用的多属性决策方法[13]，该方法通过比较各方案的差异程度，从而得到评估指标权重，可以比较客观地反映样本间的现实关系。为此，本文利用离差最大化方法对地铁车站拥挤踩踏事故风险评价问题进行研究。

2 车站踩踏风险评价指标体系

构建科学、合理的评价指标体系是分析及评估地铁车站踩踏风险大小需要解决的首要问题。借鉴目前既有研究成果[8，10]，根据国内地铁车站发生拥挤踩踏事故的案例情况，本文建立了地铁车站拥挤踩踏事故风险的评价指标体系，如图1所示。

（1）人群拥挤密度（C1）指标[14-15]。该指标主要是指地铁车站中每平方米的乘客数。车站人群密度越大，越容易发生拥挤，拥挤踩踏事故风险也随之增加。

（2）逆向对冲人数比（C2）指标。该指标主要是指在一个统计周期内少数逆向人数与多数正向人数的比值。逆向对冲人数比越大，表明人流对冲越严重，越容易发生踩踏事故。

（3）疏导员平均服务面积（C3）指标。该指标主要是指单个疏导人员服务的站台面积。该指标数值越大，疏导人员完成疏导面积也越大，拥挤踩踏事故发生的概率也随着增加。

（4）乘客平均步速（C4）指标。该指标主要是指乘客平均行走的速度。乘客平均步速越大，乘客疏散越快，造成拥挤踩踏事故风险越低。

（5）列车进站时间间隔（C5）指标。该指标主要是指相邻列车行车进站时间间隔。列车进站时间间隔越小，地铁车站站台滞留的乘客越少，发生拥挤踩踏事故风险也越低。

（6）车站环境（C6）指标。该指标主要是指车站的通道布局、通道宽度以及扶梯等基础设施方面。该指标得分越高，说明该车站设计越符合设计标准要求，其发生拥挤踩踏风险也越低。

（7）弱势人群比例（C7）指标。该指标主要是指老、幼、病、残、孕等人数占总人数的比例。弱势人群比例越大，表明人流局部紊乱程度越大，其发生拥挤踩踏风险也随之增加。

3 车站踩踏事故风险评价方法

考虑到地铁车站拥挤踩踏风险评估是一个属性权重完全未知的多属性决策问题，假设参与拥挤踩踏风险评估有n个车站和m个属性，其决策矩阵表示为A=（aij）n×m，其中，aij为第i个方案的第j个指标属性值。通过规范化处理后，决策矩阵A转化为标准化决策矩阵X=（xij）n×m。假设评估对象m个属性权重为wj =（w1，…wm）。则第n个评价方案的综合值zj可以用公式（1）表示，具体计算公式如下：

（1）离差最大化法[13]是利用车站拥挤踩踏风险评价指标属性值离散程度大小确定相应的评价指标权重。对于车站拥挤踩踏风险评价而言，若某一个评价指标的离散值差异较大，说明该评价指标对车站风险评价结果影响越大;反之，该评价指标对评价结果影响越小。鉴于此，在满足归一化和权重约束原则的条件下，根据所有评价对象的所有评价指标的总方差最大化原则，建立了地铁车站拥挤踩踏风险权重计算模型。该模型目标函数如公式（2）所示，具体计算公式如下：

（2）式（2）中， D（w）表示对于所有评价指标而言，所有评估方案的总离差;Dij（w）表示对于aj指标而言，方案ai与其他所有评估方案的离差;xij为第i个方案的第j个指标属性值，xkj分别为第k个方案的第j个指标属性值;i =（1，2，…，n）是第i个方案;k =（1，2，…，n）是第k个方案;j =（1，2，…，m）是第j个评价指标;wj表示第j个评价指标的权重。

4 实例分析

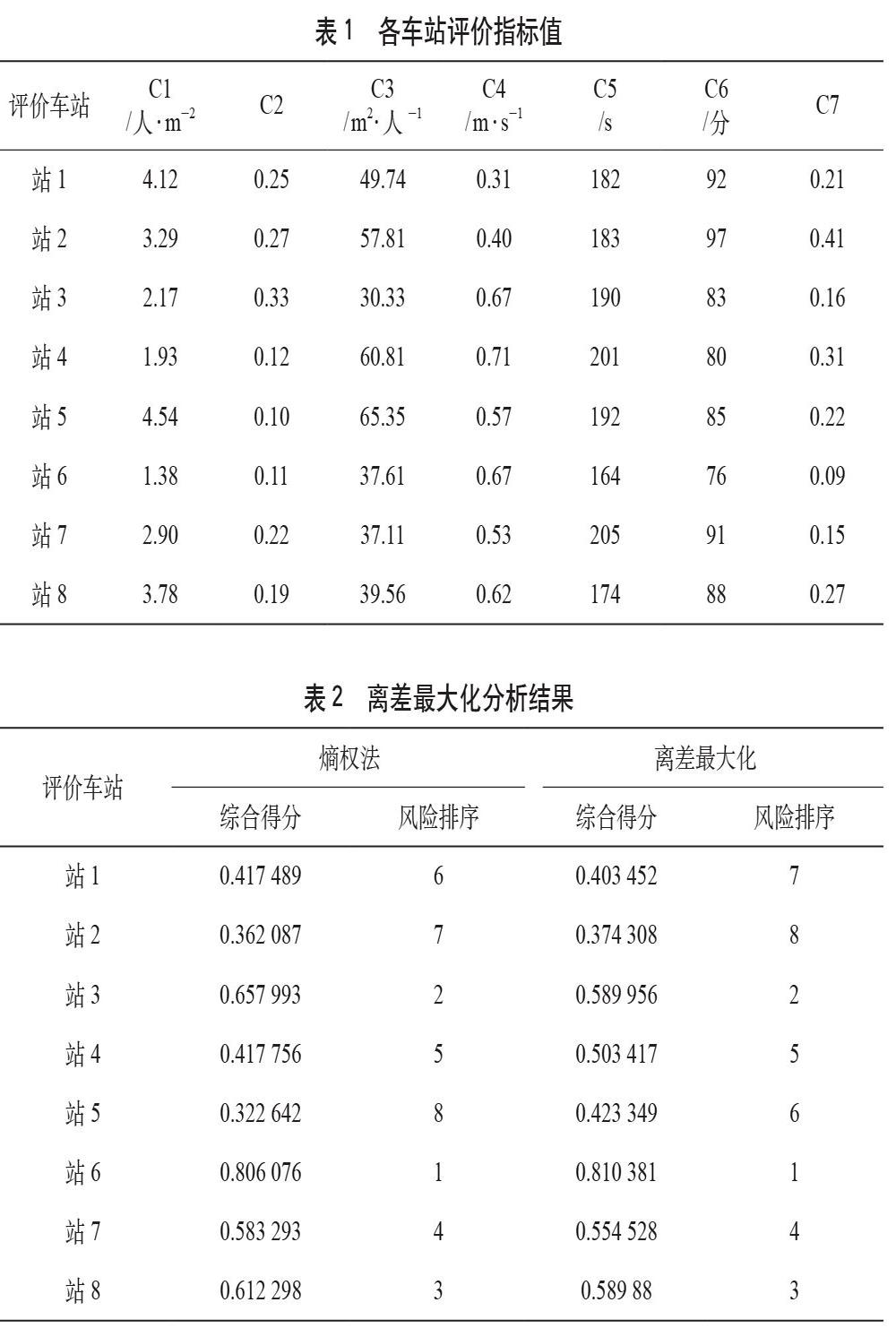
为验证离差最大化方法在评价地铁车站拥挤踩踏事故风险大小中的应用效果，本文以8个地铁车站为研究对象，对这些车站拥挤踩踏事故风险大小进行了分析与评价[10]。其中，各车站相关指标的统计数据如表1所示。

在对指标归一化处理的基础上，根据公式（2）求得各评价指标的权重向量w=（0.149 ，0.151，0.153，0.142，0.138，0.137，0.130），并根据公式（1）计算出各个车站拥挤踩踏风险评价值，并与基于熵权法的地铁拥挤踩踏事故风险评价进行对比，结果见表2。

根据综合值越大表明风险越小的原则，基于离差最大化方法对8个地铁车站拥挤踩踏事故风险由小到大进行排序，依次为车站6<车站3<车站8<车站7<车站4<车站5<车站1<车站2;基于熵权法对8个地铁车站拥挤踩踏事故风险由小到大进行排序，依次为车站6<车站3<车站8<车站7<车站4<车站1<车站2<车站5。从评估结果可以看出：除车站1、车站2和车站5外，基于离差最大化和熵权法得到的各地铁站拥挤踩踏风险评估结果相同，说明本文建立的方法能够对地铁车站拥挤踩踏风险进行分析及评价;同时，基于离差最大化的评价结果在车站1、车站2和车站5与文献[10]基于组合权重的地铁车站拥挤踩踏事故風险评价结论一致，这也进一步说明本文模型在地铁拥挤踩踏风险评估的有效性。

5 结语

地铁车站拥挤踩踏事故风险的分析及评价是地铁运营单位编制拥挤踩踏事故应急预案的基础，对于提高地铁车站安全管理水平、保证地铁正常运转等方面具有重要意义。考虑到评价指标权重在地铁车站拥挤踩踏事故风险评价中的重要作用，将地铁拥挤踩踏风险评价问题看作是多属性决策问题，基于离差最大化的思想，本文利用离差最大化模型对地铁车站拥挤踩踏事故风险进行评价。研究结果表明离差最大化方法能够充分利用客观信息评估车站拥挤踩踏风险，降低主观因素在地铁车站拥挤踩踏事故风险分析及评估中的不确定性。

参考文献

[1]卢文刚，黄小珍. 城市地铁踩踏事件应急管理研究——基于2008-2017年典型案例的分析[J]. 中国应急救援， 2017（4）：4-9.

[2]王艳，彭超，魏嘉池. 基于时空拥挤度的地铁拥挤踩踏事故实时监测预警系统[J]. 都市快轨交通，2018，31（1）：99-104.

[3]王起全. 地铁拥挤踩踏事故脆弱性区域智能化预警研究[J]. 中国安全科学学报，2018，28（11）：166-171.

[4]朱昌锋.基于DEA的城市轨道交通运营安全评价与分析[J].兰州交通大学学报，2010，29（3）：67-70.

[5]王志华. 地铁车站运营安全风险评价研究[D]. 北京：北京交通大学，2012.

[6]王起全. 基于赋权关联度算法的地铁拥挤踩踏事故风险研究[J]. 中国安全科学学报，2013（5）：95-101.

[7]佟瑞鹏，李春旭，郑毛景. 拥挤踩踏事故风险定量评价模型及其优化分析[J]. 中国安全科学学报，2013，23（12）：90-94.

[8]刘艳，汪彤，丁辉. 地铁车站拥挤踩踏事故风险评价DEA模型研究[J]. 中国安全科学学报，2013，23（10）：100-104.

[9]角志达，宋瑞，刘星材. 城市轨道交通车站拥挤踩踏事故风险评价[J]. 交通信息与安全，2015（2）：86-91.

[10] 霍宇芒，宋守信，顾一波. 基于组合权重的地铁车站拥挤踩踏事故风险评价[J]. 安全与环境工程，2016，23（5）：139-143.

[11]尹晓庆. 基于FFTA-FCE的地铁站拥挤踩踏事故风险评估[D].湖北武汉：武汉理工大学，2018.

[12]于恒，汪益敏，仇培云. 基于可拓理论的地铁车站多风险因素安全评价体系[J]. 交通工程，2019，19（2）：74-80.

[13]王应明. 运用离差最大化方法进行多指标决策与排序[J]. 系统工程与电子技术，1998（7）：24-26.

[14] 王起全. 基于赋权关联度算法的地铁拥挤踩踏事故风险研究[J]. 中国安全科学学报，2013，23（5）：94-100.

[15]冉丽君，刘茂. 人群密度对人群拥挤事故的影响[J]. 安全与环境学报，2007，7（4）：135-138.

[16] 贾天耀，张波，孙春光，等. 地铁车站增设人员流动物理干预设施安全风险研究[J]. 现代城市轨道交通，2018（11）：59-62.

[17] 李子浩，田向亮，黎忠文，等. 基于客流规律的地铁车站客流风险分析[J]. 清华大学学报（自然科学版），2019（10）：854-860.

[18] 王校，景艳红. 地铁车站运营安全风险评价体系研究[J]. 城市建设理论研究，2019（15）：156.

[19] 曾明华，王旭，王转敏，等. 基于模糊多态贝叶斯网络的地铁运营风险评估方法[J]. 城市轨道交通研究，2019（5）：28-33.

[20] 潘福全，泮海涛，亓荣杰，等. 地铁密集人群风险等级与预警标准研究[J]. 交通科技与经济，2019（5）：6-11，19.

[21] 梁修诚，李晔，李文翔. 基于公交卡数据的地铁站点客流集聚风险评价研究[J]. 综合运输，2019（9）：64-69.

[22] Jie Wang， Gui-wu Wei， Cun Wei， et al. Maximizing deviation method for multiple attribute decision making under q-rung orthopair fuzzy environment [J]. Defence Technology，2019（12）：1-15.

[23] 黄小珍. 基于模糊综合评价法的城市地铁踩踏事件应急能力评价——以广州地铁为例[D]. 广东广州：暨南大学，2017.

收稿日期 2019-12-19

责任编辑 胡姬