万变不离其宗 起落皆有定数——三角函数图象类问题的图表对照法例析

赵明丁

(广东省佛山市顺德区第一中学 528300)

一、众里寻她千百度——扑朔迷离中的困惑

三角函数图象及性质为高考必考内容，主要考查：

(1)三角函数的最值、周期性、单调性、对称性等性质；

(2)函数图形的平移、伸缩、反射变换等；

(3)方程或不等式代数运算等.由于该内容涉及较多公式(包括诱导公式、倍角公式、和差角公式和相关点坐标和相关轴线公式等)，而且题型多样、结构灵活，对学生能力要求较高.乱花渐欲迷人眼，能否“九九归一”寻求一种通法，以不变应万变，将它们一网打尽呢？

二、一图一表总关情——在探索总结中提炼精华

三角函数图象类的常见题型有:

(1)由函数图象求其代数表达式进而研究其相关性质；

(2)由函数解析式，研究函数图象的点坐标、对称轴或单调区间；

(3)由三角函数性质或图象，研究参数的值或取值范围；

(4)三角函数图象及性质与其它知识的综合.

题型众多，能否有统一的解题法？本文提出一种图表对照法，即利用“一幅图”和“一张表”对照辅助解题的方法.由于形如y=Asin(ωx+φ)+b或y=Acos(ωx+φ)+b的一般三角函数的图形都可由基本的正弦函数y=sinx图象通过一系列坐标变换所得，如果能将题目所研究的三函数的自变量取值以及相关图形特征都回归到基本正弦曲线中，用数形结合的思想，问题就简单明了.以下例析阐释.

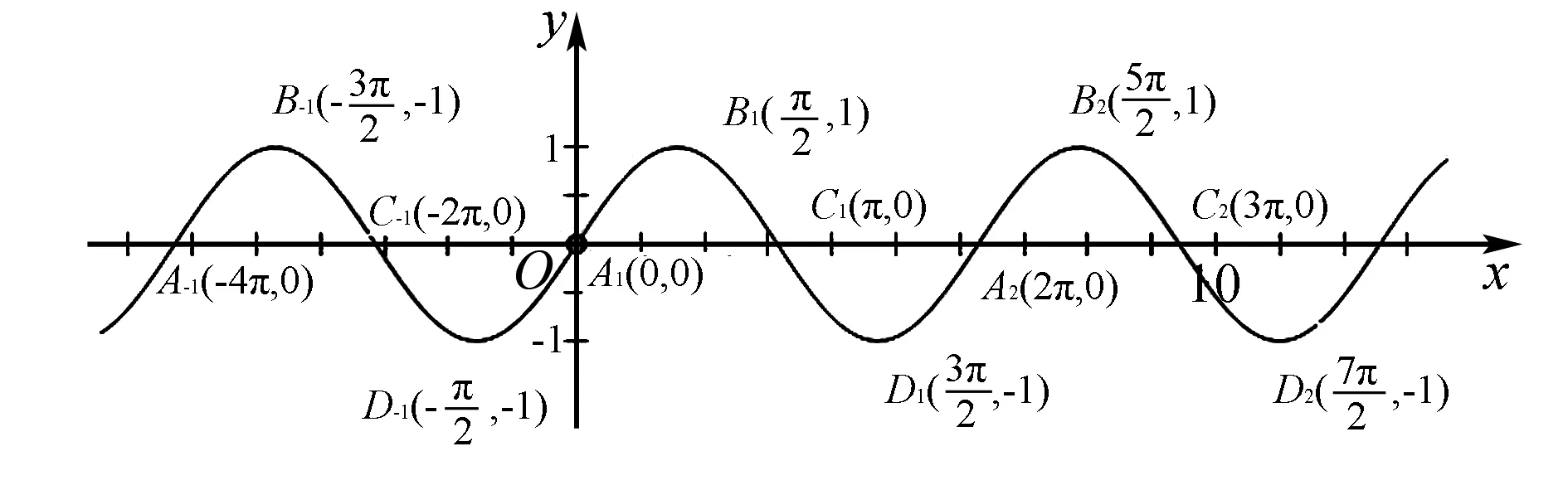
图1

分析先画出基本正弦函数图象，如图1所示，在图中A1，B1,C1,D1代表了x轴正方向第一周期的四个关键点，下标为2代表第二周期，下标为-1代表负方向第一周期，依次类推，图象可根据需要向两边延展，本文例题将反复使用图1进行对照研究.接着，在表格中按从小到大的顺序列出题中所涉及的自变量x的值，计算括号内的角的对应值X，并写出各取值与图1中的图象的对应位置或相对位置，如表1所示.

表1

评析上法充分利用了我们最熟悉的基本正弦曲线的直观图形辅助解题，同时用表格的形式清晰列出题中涉及的自变量x所有取值(包括参照值0)、括号内的量X的值及他们对应图1的位置或相对位置，然后根据表格可列出方程或不等式，求解得答案.

三、吹尽黄沙始到金——在解题实战中升华方法

上例详细分析了用“图表对照法”探究三角函数中参数的取值范围问题，以下将采用该法来解其它题型.

题型1根据三角函数图象，确定参数的值

通过与参照点数量比较，只能落在D1处，所以可得表2所示的对应关系.

表2

题型2确定三角函数在给定区间中的最值

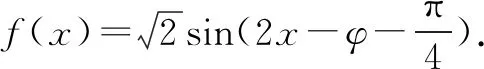
表3

答案为A.

评析本题的解法大多是通过研究周期得到ω的取值范围，经过计算再求出φ的可能取值，然后再验证单调

性是否得到满足，其推理过程比较复杂，如用上法，思维简化，运算也不复杂，能够更快、更准地得到答案.

四、映日荷花别样红——在反思对比中参透本质

求解三解函数图象及性质相关的问题时，尤其是客观题时，“回溯本原”，把三角函数相关问题放在基本正弦曲线上研究，结合图象和表格确定数量和位置间的对应关系，省去中间较为复杂推理和演算过程.该方法紧扣函数图象本质，立足知识的”根本”，若能在解题实践中将本方法灵活应用，必能达到“枝繁叶茂”的效果，体会到这种“图表对照法”的优越性.