基于蚁群算法的TPS问题求解策略研究

徐 畅 张浩漩

(重庆邮电大学 重庆市 400000)

一、TSP问题是什么

(一)问题概述

TSP问题是一个典型的组合优化问题。比如，一位商人从自己的家乡出发，希望能找到一个最短的道路，这一条道路要经过给定的所有城市，最后一个城市回到自己的家乡。并且路过每个城市一次，且仅一次。如果构造一个图：图中的顶点为城市，顶点间的边表示城市间的交通线，边上的权为沿该交通线旅行的费用。那么，TSP问题就抽象为在这个图中寻找最短哈密尔顿回路。

(二)数学模型

TSP问题表示为一个有N个城市的有向图G=(N,A)。其中N={1,2,3,…，n}，城市之间的距离为(不一定是对称矩阵，实际问题决定)。目标函数为(即总路径长度)。

二、利用蚁群算法求解TSP问题

(一)蚁群算法概述以及基本原理

蚁群算法最初是通过对蚂蚁的观察，受蚁群行为特征启发，而得出的一种算法。蚂蚁是一种群居昆虫，他们在日常生活中彼此协调，相互依赖，共同完成任务。单个蚂蚁做不到的事情，整群蚂蚁却可以完成。[1]

蚂蚁在运动过程中，能够在它所经过的路径上，留下一种称之为信息素的物质。信息素是蚂蚁个体之间信息传递交流的载体。蚂蚁在运动时，能够感知这种物质，并且习惯于追踪此物质，追踪过程中，继续释放信息素。一条路上的信息素踪迹越浓，其它蚂蚁将以越高的概率，跟随此路径，从而该路径上的信息素踪迹会被加强。因此，由大量蚂蚁组成的蚁群的集体行为，便表现出一种信息，正反馈现象。某一路径上走过的蚂蚁越多，则后来者选择该路径的可能性就越大。蚂蚁个体之间，就是通过这种间接的通信机制，实现协同搜索最短路径的目标。蚁群算法这种启发式算法的出现，解决了组合爆炸的问题，其可以在合理的时间范围内找到可接受的最优解。

(二)TSP问题求解过程

基于以上所述的自然界中的蚁群行为，我们可以将TSP问题抽象为求解最短的蚂蚁觅食路径。我们人工构建的蚁群具有一定的记忆能力，能够记下已经访问的城市。同时，信息素衡量标准可以改变，蚂蚁每次选择的下一个城市是确定的，而不是盲目的，通过概率计算下一个所要经过的城市。[2]

同时，我们将TSP问题中所给的城市画为一无向图，在蚁群算法中，旅行商，即模型中的蚂蚁，在图的邻接点之间不断移动，从而找到最短路径。而从某一点选择另外一点的转移概率，由图的每条边的权值决定，这里的权值即蚁群散发的信息素浓度。每次选择一条路，该路上的信息素浓度都会更新，而其更新的形式有两种，一是挥发，即该路信息素由于无人经过，而以比例减少；二是增强，即有蚂蚁走过时，该条路的信息素浓度会相应变大。

人工蚂蚁和旅行商走到下一个城市的概率，是通过一个随机规则实现的，即运用当前信息素和可见度所储存的信息，计算出下一步可达点的概率，并按概率可能实现下一步的移动。从此往复运算，越来越接近最优解，即最短路径。蚂蚁在寻找过程中，寻找到其中一个解后，会记录下来和其他解比较，直至找出最短路径最优解。

1.路径构建。核心步骤之一为构建合理的路径供蚂蚁选择。我们可以令TSP问题中的蚂蚁随机选择一个城市作为出发城市，初始时刻，各条路径上的信息素量相等。

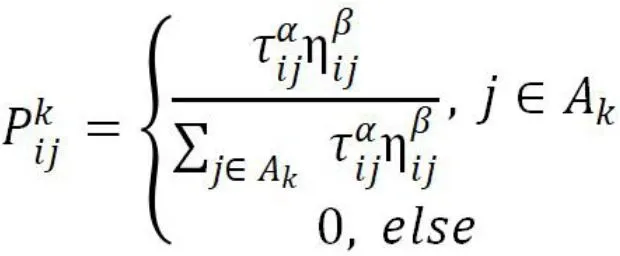
2.信息素更新。核心步骤之二是信息素的更新，通过信息素的更新才能实现蚂蚁对路径的选择。当蚂蚁选择到一条路径之后，就对信息素进行更新，算法开始的时候会有一个固定的信息素值C，每次走过相应路径，信息素会挥发或增加，并经过多次迭代。初始值的C不能过高，也不能过低。如果C过低，算法容易早熟，过早找到的路径不一定是最短的，C太大就会影响效率。每经过一轮后，其释放的信息素公式如下：

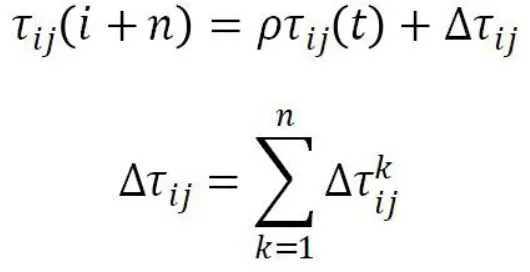
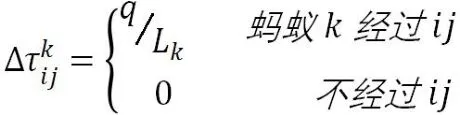
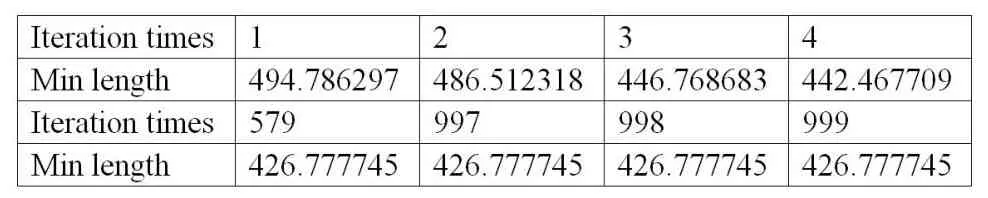
3.实际问题求解。实际问题中，我们假定了30个城市的坐标，30×30的地图，对蚁群算法进行应用，即三个城市的TSP问题求解。随机设定了30个城市的坐标，定义蚁群数量也为30个，为了精确最小路径的数值，我们将迭代次数尽量放大，设定为1000次。同时，为了保持城市坐标的随机性，我们引入了time(0)函数来获取随机秒数。同时，在蚂蚁选择下一个城市时，计算标准除了利用概率，还利用轮盘赌法进行选择，并且蚂蚁可以进行城市之间的移动和搜索城市。更新环境信息素时，当前每条路上的信息素，等于过去保留的加上每个蚂蚁这次走过这条路留下来的信息素。接下来最重要的一步，就是寻找最短路径的部分，遍历所有的蚂蚁经过他们的城市道路后，将最好的蚂蚁路径保存下来，只要有蚂蚁路径比其他的完好就保存下来，经过1000次迭代，就可以很大程度的趋近于最近的一条道路。

最终结果大致如下：

?