浅埋隧道盾构掘进地层挤出破坏形态与临界压力上限有限元分析
2020-03-30王利莹
王利莹
(中铁十八局集团第五工程有限公司,天津 300222)
盾构掘进过程中土压力控制对于维持开挖面和地层稳定相当重要。土压力控制不当易产生地层坍塌或隆起,对周围环境造成较大的影响。近年来,极限分析[1-3]成为浅埋隧道稳定性分析的又一种手段,其中以上限法居多。谢骏等[4]从塑性极限分析上限法的基本原理出发,通过分析单圆形隧道4 种类型垮落机制所获得的稳定率上限解,构建了双平行圆形隧道的破坏机制;杨峰等[5]利用2 种破坏模式分析了矩形浅埋隧道围岩压力问题,指出利用极限分析上限法计算浅埋隧道围岩压力的方法可行;Davis 等[6]提出 4 种简化破坏模式,利用极限分析上限法研究了黏土地层浅埋隧道的稳定性。赵明华等[7]应用极限分析有限元法,对方形隧道稳定性开展数值模拟,获得稳定系数的经验公式和隧道破坏模式。张箭等[8]针对浅覆盾构隧道环向挤出破坏,应用刚体平动运动单元上限有限元法进行了计算分析;贺志军等[9]针对纵向倾斜地表盾构隧道掌子面三维挤出问题,开展了上限破坏分析,探讨了掌子面支护力的变化规律。
现有文献中关于采用上限有限元方法分析盾构推进过程中临界压力和地层挤出破坏形态的影响因素的研究相对较少。本文采用六节点三角形单元上限有限元法开展计算分析,主要研究地层岩性、隧道埋深、土体剪胀等因素影响下浅埋隧道盾构掘进地层挤出破坏形态和地表隆起临界压力,为盾构土压力和地表隆起变形控制提供参考。
1 浅埋隧道地层挤出破坏有限元分析
1.1 分析方法
盾构推力过大导致地层挤出是三维空间问题,这里简化为沿隧道横截面的平面应变问题。
浅埋圆形隧道地层挤出破坏平面应变分析模型见图1。其中:D为隧道直径;H为埋深;γ为土体重度;φ为内摩擦角;c为黏聚力。σtcr为隧道上覆地层恰好发生挤出破坏时对应的临界压力。
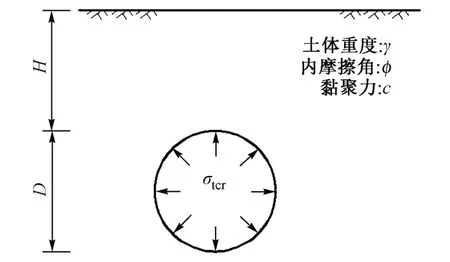
图1 浅埋隧道地层挤出破坏平面应变分析模型
定义σtcr/c为临界压力系数,则有

σtcr/c为内摩擦角φ、重度比γD/c、埋深比H/D的函数,其数值由上限有限元法[10]计算获得。
1.2 上限有限元分析模型
浅埋隧道地层挤出破坏上限有限元模型网格和边界条件(H/D=2,取隧道右侧1/2)见图2。模型竖向向下延伸L1,水平向右延伸L2,以消除边界效应。L1,L2分别取25,50 m。

图2 浅埋隧道地层挤出破坏上限有限元模型网格和边界条件
考虑到挤出破坏发生在隧道正上方和斜上方区域,对这些区域网格进行了加密,共划分了5 467 个单元。不同埋深比对应的网格与图2类似。
隧道圆心为模型坐标原点O。六节点三角形单元上限有限元法[10]每个单元节点含2 个速度分量,底部和右侧边界均同时约束x轴和y轴方向的速度。左侧边界约束x轴方向的速度,地表为自由边界。
为求解σtcr/c,需在隧道轮廓上施加均布力。施加均布力时

式中:S为单位面积;dS表示沿隧道轮廓s方向上的塑流体积,法向方向指向隧道围岩一侧为正为法向速度分量。
对于浅埋隧道地层挤出破坏上限有限元模型,其目标函数=系统耗散能-自重虚功率。目标函数的最小值为隧道上覆地层恰好发生挤出破坏时对应的临界压力σtcr。上限有限元的线性规划模型[10]为
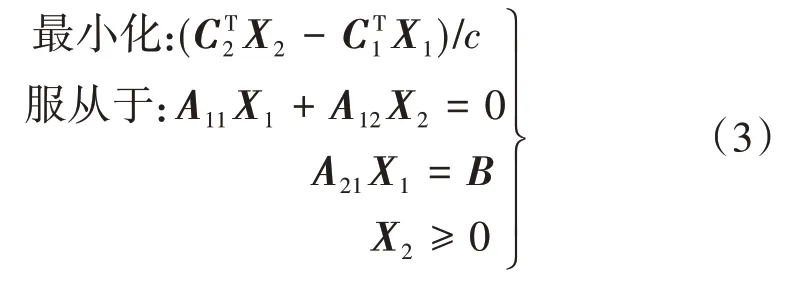
式中:X1为节点速度分量ui和vi组成的向量;X2为单元塑性乘子组成的向量为系统耗散能之和;为地层自重虚功率;A11,A12,A21为全局变量;B为速度边界等式约束向量。
假定摩尔-库伦屈服准则线性化参数为36,计算理论见文献[10]。
1.3 计算参数的确定
为考察不同参数(φ,γD/c,H/D)[11]对σtcr/c的影响规律,计算参数按表1取值。

表1 浅埋隧道地层挤出破坏计算参数
φ和c的选取考虑了实际岩土材料,兼顾了无量纲正交化计算的需求。当φ较大时,必须考虑剪胀效应对临界压力系数的影响。参考文献[10],引入剪胀角ψ,设置等效参数φ*和c*。

本文取ψ/φ=1和ψ/φ=0两种情况进行分析。
2 模拟结果分析
2.1 临界压力系数σtcr/c分析
采用上限有限元程序[10],按1.3 节各参数取值正交组合出252 种工况。隧道施工地层挤出σtcr/c上限有限元计算结果见表2。
各参数对σtcr/c的影响曲线见图3。
由图3(a)可以看出:σtcr/c随φ增大而增大;且γD/c越大,σtcr/c增大越明显;反之,γD/c较小时,σtcr/c更接近于水平直线。虚线示意了文献[10]刚体平动运动单元上限有限元分析结果,与本文结果高度一致。
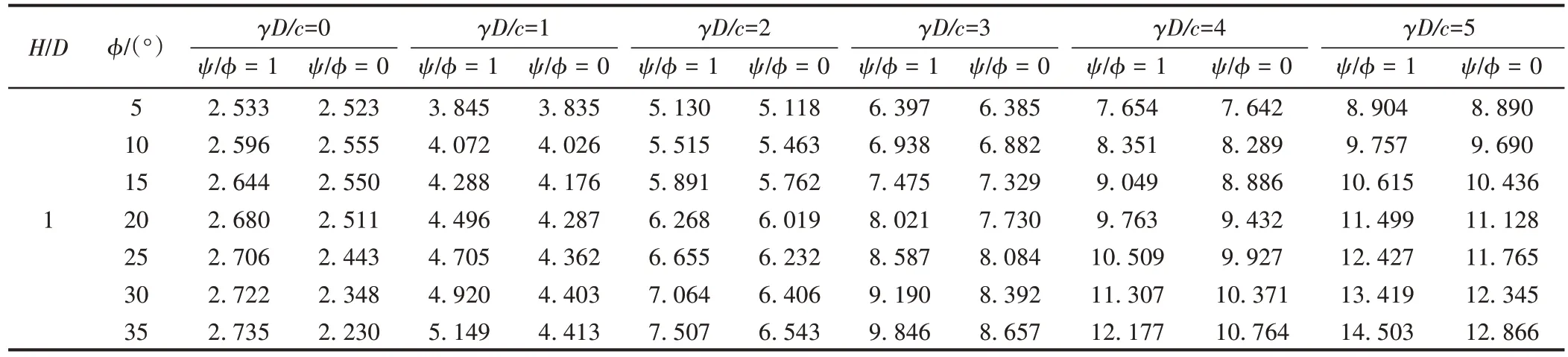
表2 隧道施工地层挤出σtcr/c上限有限元计算结果
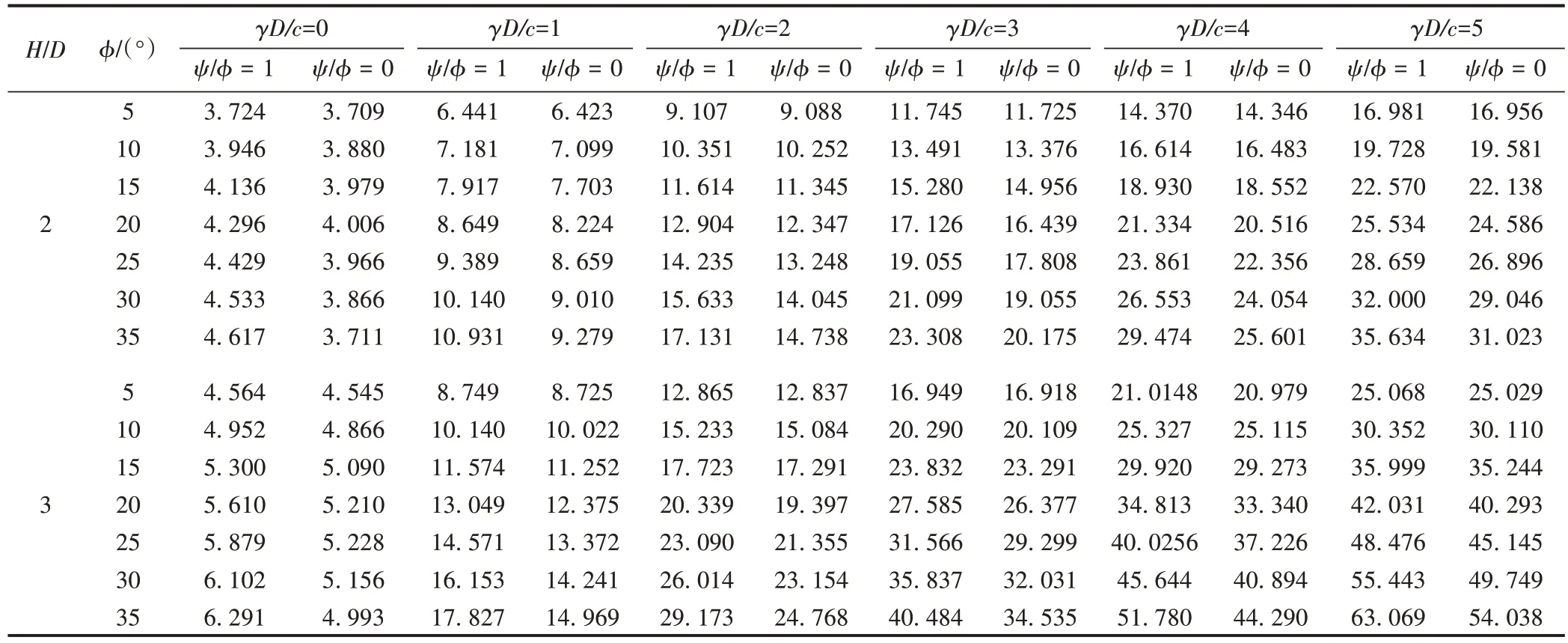
续表2
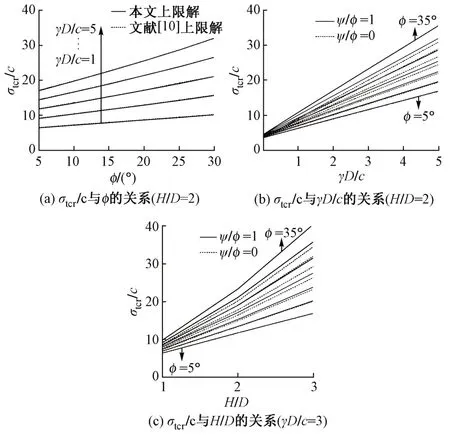
图3 各参数对σtcr/c的影响曲线
由图3(b)中将ψ/φ=0 对应的结果以虚线示出。可以看出:σtcr/c随γD/c变化基本呈线性增加,表明自重对挤出破坏发生起主导作用。随着φ的增加,σtcr/c直线斜率增加。对于ψ/φ=0的情况,φ较小时,σtcr/c与ψ/φ=1 对应结果差异不大;而φ较大时,ψ/φ=0 对应的σtcr/c值明显较ψ/φ=1时小。
由图3(c)可以看出:σtcr/c随H/D基本呈线性增加,当φ较大时(如φ= 35°),σtcr/c随H/D的增大呈非线性变化趋势。
2.2 破坏模式分析
当γD/c= 3,φ= 20°,H/D= 1 时,地层挤出破坏上限有限元网格和耗散能密度分布见图4。图中只显示了水平方向0~1.5D,竖直方向-1.0D~1.5D的计算区域。稀疏网格有428 个单元,密集网格有4 521 个单元。耗散能密度为单元耗散能与面积的比值,并依据最大值进行了归一化处理。其反映了地层挤出破坏发生时土体中的剪切带或塑性区。
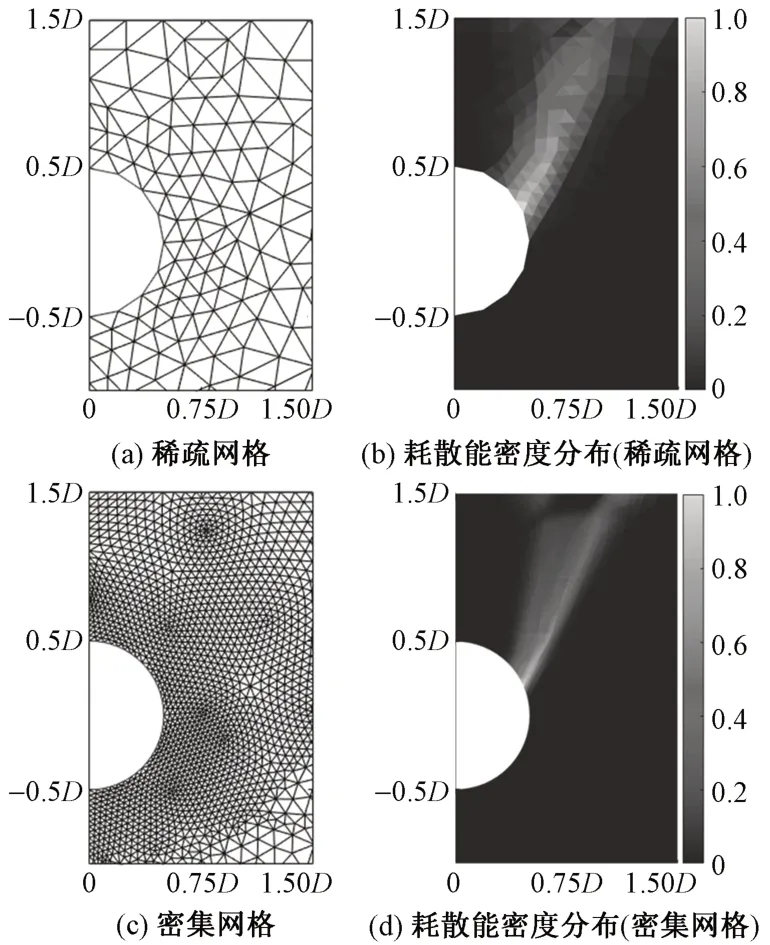
图4 地层挤出破坏上限有限元网格和耗散能密度分布
从图4 可以看出:网格稀疏时耗散能密度分布的范围较大,耗散能密度较大区域不集中;网格密集时耗散能密度较大区域明显呈带状,靠近隧道轮廓处耗散能密度最大,地表处最小。
网格稀疏和网格密集时对应的σtcr/c分别为8.278和8.021,后者比前者小3.1%。按上限理论,后者精度较高。本文计算均采用密集网格。
各参数对破坏模式的影响规律见图5。
由图5(a)和图5(b)可以看出:φ较大时耗散能密度呈明显的斜向条带状分布,向上隆起的范围比φ较小时大;而φ较小时耗散能密度分布区域更宽,从隧道起拱线处向上弯曲到达地表,形成的破坏范围更大。
由图5(c)和图5(d)可以看出:γD/c较大时,耗散能密度呈更窄更集中的斜向条带状分布,至地表有所发散;而γD/c较小时,耗散能密度分布区域变得更加宽大,从隧道边墙处向上弯曲,到达地表后发散更明显,破坏范围更大。

图5 各参数对破坏模式的影响规律
当γD/c=3,φ=20°,H/D=3 时,地层挤出破坏发生时网格变形见图6。可以看出,挤出区域出现在隧道正上方,地表鼔出近似呈倒置的锅底。隧道正上方至地表相当大范围内地层整体向上运动,斜向上方向变形最大。虚线为隧道原轮廓线,其上帽子状区域即为隧道内挤出土体。因破坏时的体积增大效应,该土体体积小于地表鼔出土体体积。
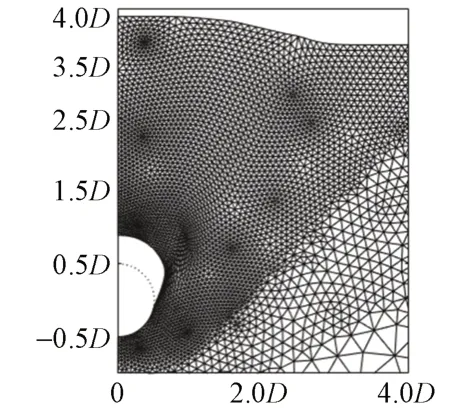
图6 地层挤出破坏发生时网格变形
其他参数条件下的挤出破坏网格变形与此类似,不作赘述。
埋深比越大,剪切带起始位置越靠下,剪切带在隧道斜上方发生弯曲的程度越大。
3 结论
采用六节点三角形单元上限有限元法进行盾构隧道施工地层挤出破坏分析,结论如下:
1)临界压力系数随土体内摩擦角增大而增大,且重度比越大临界压力系数增加得越明显;当重度比较小时,临界压力系数与内摩擦角关系曲线接近于水平直线;临界压力系数随重度比和埋深比的变化基本呈线性增长;当内摩擦角较大时,剪胀效应使临界压力系数明显增大。
2)内摩擦角较小时,剪切带从隧道起拱线处向上弯曲到达地表,区域较宽,形成的破坏范围较大;内摩擦角较大时,耗散能密度呈斜向条带状分布,向上隆起的范围较大。重度比较大时,耗散能密度呈更窄更集中的斜向条带状分布,至地表有所发散;埋深比越大,剪切带起始位置越靠下,剪切带在隧道斜上方发生弯曲的程度越大。
3)地层挤出破坏区域出现在隧道正上方,地表鼔出近似呈倒置锅底。隧道正上方至地表相当大范围内地层整体向上运动,斜向上方向变形最大。
