锚杆加固恩施大峡谷绝壁危岩的稳定性数值分析

谭朝瑞,王明华,付 强,袁 飞,刘易然

(湖北省地质局第二地质大队，湖北 恩施 445000)

锚杆锚固技术已成为一种不可替代的岩土工程安全加固措施，在边坡岩体经过开挖卸载后，表层失衡的自重应力场通过锚固作用得到适当恢复，主要作用为对表层卸荷岩体的压实压密，增韧止裂，提高岩体整体性与变形均匀性，降低了局部破坏的机率，形成了新应力状态的良性调整[1-3]。因此许多专家学者通过理论计算或者监测数据分析的方法也对锚杆部分加固参数与稳定性的关系做出来了许多创新性的研究[4-9]。有限元法作为一种运用广泛的数值分析方法，具有功能强大，分析结果明确等优点，一些学者结合锚杆的部分加固参数，也开展了数值模拟方面的研究[10-17]。本文采用ABAQUS有限元软件，对锚杆加固参数的作用效果进行分析，分别选取锚杆的长度、入射角、数量、间距多情况进行模拟，并进行综合对比分析，得到大峡谷绝壁栈道危岩加固最为经济安全的选择。

1 危岩概况

绝壁陡崖危岩位于湖北省恩施大峡谷绝壁栈道景区，属构造剥蚀侵蚀中低山区，出露地层岩性主要为三叠系下统大冶组三段(T1d3)薄层状灰岩，呈近水平产出，风化程度不均，整体呈微—中风化，局部陡崖顶有少量第四系全风化层，单层厚度一般8 cm～15 cm，总层厚约1 m～2 m。

如图1所示，危岩分布高程1 767.4 m～1 788.2 m，总体呈巨块状，整体高约21 m，平均宽约8 m，平均厚度4 m，体积约672 m3。危岩受两组垂直的裂隙切割，正面、右侧临空，底部完全悬空，只有左侧和后部与母岩相连。

图1 危岩基本特征

2 研究方法

本次模拟采用ABAQUS有限元分析软件开展数值模拟研究。ABAQUS有限元模拟中危岩边坡稳定极限平衡方法采用Mohr-Coulomb屈服准则，安全系数定义为沿滑动面的抗剪强度与滑动面上实际的剪力的比值，用公式表示如下：

(1)

式中:ω、s和τ分别为安全系数、滑面上的抗剪强度和滑面上的实际剪切力；c、φ分别为岩体的黏聚力和内摩擦角。将式(1)中强度参数除以ω得到：

(2)

(3)

有限元强度折减法通常采用下式定义安全系数：

(4)

式中:I1和J2分别为应力张量的第一不变量、应力偏量的第二不变量；α和k是与岩土材料黏聚力c和内摩擦角φ有关的常数，采用与Mohr-Coulomb准则等面积圆的广义米赛斯屈服准则，计算的塑性区反映围岩实际塑性区的大小，广义米赛斯屈服准则的系数α和k为：

(5)

(6)

可见，在D-P准则中α和k折减的同时，c和tanφ也有同步折减关系，式(5)和式(6)是两者折减系数间换算关系。式(4)中，ω是强度折减法中安全系数的定义。强度折减有限元方法的基本原理是将岩体强度参数黏聚力c和内摩擦角φ同时除以一个折减系数ω,得到一组新的c′和φ′值，作为新材料参数输入，进行试算；当计算不收敛时，对应的ω值为边坡的最大稳定安全系数。

本文采用了未降雨和降雨后两种工况模拟危岩的稳定性，模拟参数如表1所示。

选用危岩的防护治理为研究对象，考虑其不同锚杆参数选择在稳定性的区别，参数选择如表2所示。

表1 灰岩模拟参数

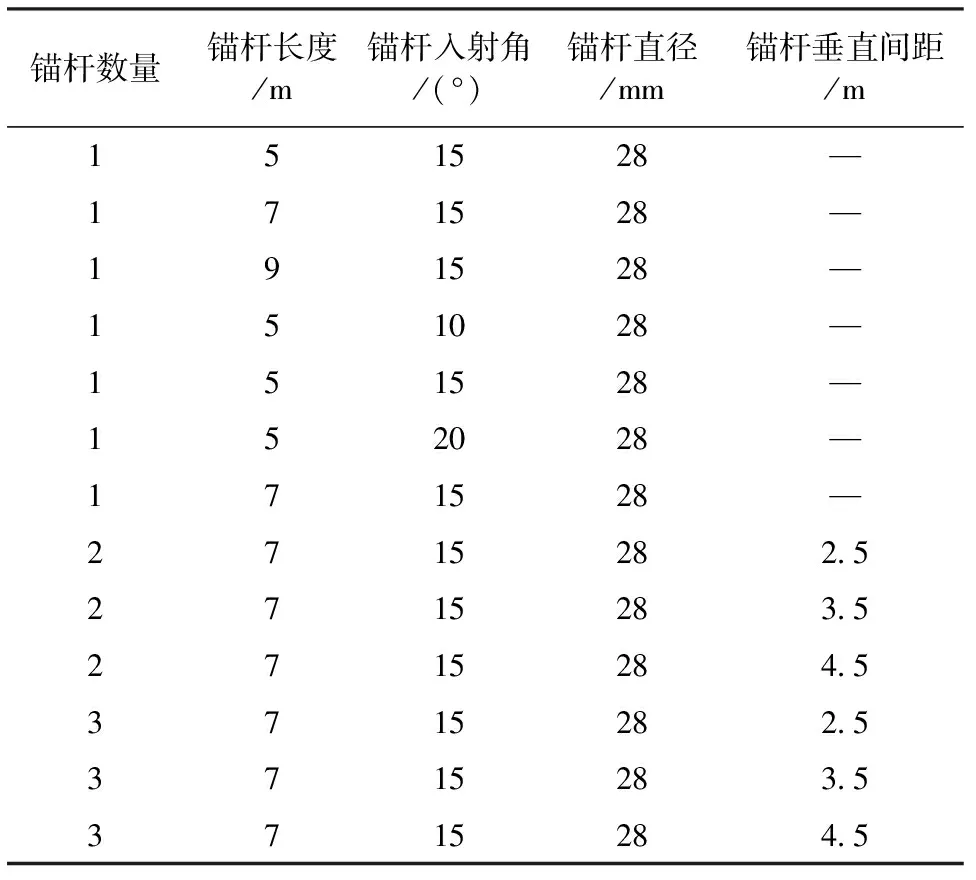
表2 锚杆加固参数选择

其中模型参数不变，在危岩位置加设锚杆，根据锚杆物理力学参数，弹性模量取210 GPa，泊松比取0.3，密度取7 850 kg/m3。模拟云图结果应力单位为Pa，位移单位为m。根据危岩和实际工程情况，锚杆直径统一为28 mm，且长度不宜过长，因此选取5 m、7 m、9 m三种锚杆长度，根据不同锚杆长度布置图如图2所示。

图2 不同锚杆长度布置图

锚杆入射角一般取值在10°～25°之间，当锚杆入射角度<5°时，锚杆注浆施工难度大，浆液不容易到达锚杆底部；当锚杆入射角度>25°时，锚杆提供的水平力比较小了，造成锚杆浪费，因而选取10°、15°、20°作为入射角的参数选择，如图3所示。

与此同时，在危岩锚杆治理中，通常会考虑使用多根锚杆共同作用，考虑了纵向2根、3根锚杆设置，锚杆间距分别为2.5 m、3.5 m、4.5 m，如图4、图5所示。

图3 不同锚杆入射角布置图

图4 2根不同锚杆间距布置图

图5 3根不同锚杆间距布置图

3 有限元数值模拟研究

3.1 单根锚杆不同加固参数危岩稳定性的有限元模拟

3.1.1 塑性应变结果分析

如图6所示，设置锚杆后塑性应变的分布区域不变，但应变值都有所减小，且平均最大塑性应变值相比未设锚杆降低了47.1%，但增大锚杆长度几乎不能影响塑性应变值的最大值和分布，对于后续的应力和位移分布也同样如此。因此，当锚杆长度超过推测滑动面时，持续增大锚杆长度并不能很好的提高危岩的防护效果，达到增强稳定性的效果。

如图7所示，入射角在10°～15°之间，每增加1°最大塑性应变值就增加7.1×10-4；入射角在15°～20°之间，每增加1°最大塑性应变值就增加16×10-4。因而，锚杆入射角越大，最大塑性应变值也越大，塑性应变值的增大的速度也越快。

3.1.2 应力结果分析

如图8所示，最大应力集中在锚杆下部潜在滑动面附近，入射角在10°～15°之间，每增加1°最大应力就增加1.02×108Pa；入射角在15°～20°之间，每增加1°最大塑性应变值就增加1.72×106Pa。因而，锚杆入射角越大，锚杆的最大应力也越大，但最大应力的增大的速度越慢。

图6 单根不同长度锚杆塑性应变值云图

图7 单根锚杆不同入射角塑性应变值云图

图8 不同入射角单根锚杆应力云图

3.1.3 位移结果分析

如图9所示，增设锚杆后能明显降低危岩的水平位移，其中平均最大水平位移降低0.107 m，相比未设锚杆降低47.7%，但其总体的分布特征不会改变。入射角在10°～15°之间，每增加1°最大水平位移就增大0.001 7 m；入射角在15°～20°之间，每增加1°最大水平位移就增大0.003 5 m。因而，锚杆入射角越大，危岩的最大水平位移也越大，且最大水平位移增大的速度越快。

如图10所示，增设锚杆后能明显降低危岩的垂直位移，其中平均最大垂直位移降低0.077 m，相比未设锚杆降低29.5%，但其总体的分布特征不会改变。入射角在10°～15°之间，每增加1°最大垂直位移就增大0.001 2 m；入射角在15°～20°之间，每增加1°最大垂直位移就增大0.002 4 m。因而，锚杆入射角越大，危岩的最大垂直位移也越大，且最大垂直位移增大的速度越快。

图9 不同入射角单根锚杆水平位移云图

图10 不同入射角单根锚杆垂直位移云图

综上所述，锚杆入射角越大，对危岩的控制效果和安全性就越差，对于危岩的最大塑性应变值、最大水平位移、最大垂直位移，随着入射角增大，变化速度越快；而对于危岩的应力而言，则变化速度越慢，但入射角的变化，并不会改变它们的分布特征。因此选取较小的锚杆入射角，能够提高危岩的安全性，这和施工中的实际经验是相符合的。

3.2 2根锚杆不同间距参数危岩稳定性的有限元模拟

3.2.1 塑性应变结果分析

如图11所示，设置2根锚杆时，锚杆间距为2.5 m对塑性应变的控制效果最好，相比未设置锚杆减小了72.8%，间距3.5 m和4.5 m则相比未设置锚杆减小了57.0%和58.0%。

图11 2根锚杆不同间距的塑性应变值云图

3.2.2 应力结果分析

如图12所示，设置2根锚杆时，间距分别2.5 m、3.5 m、4.5 m时锚杆的最大应力分别为1.591×109Pa、2.051×109Pa、1.815×109Pa，即锚杆间距为2.5 m时对应力的控制效果最好，且相对位置靠下的锚杆承受的应力更大。

图12 2根锚杆不同间距的应力云图

3.2.3 位移结果分析

如图13所示，是否设置锚杆对水平位移的分布特征影响甚微，锚杆间距分别为2.5 m、3.5 m、4.5 m时，相比未设锚杆分别减小了70.5%、58.9%、59.7%，即锚杆间距为2.5 m时对水平位移的控制效果最好。

如图14所示，是否设置锚杆对垂直位移的分布特征影响不大，锚杆间距分别为2.5 m、3.5 m、4.5 m时，相比未设锚杆分别减小了42.3%、36.4%、36.6%，即锚杆间距为2.5 m时对垂直位移的控制效果最好。

综上所述，设置2根锚杆时，间距为2.5 m时危岩的安全性和防护效果最好，相比未设置锚杆，能够降低72.8%的最大塑性应变值、70.5%的水平位移、42.3%的垂直位移；相比间距3.5 m和间距4.5 m，锚杆的最大应力降低了22.4%和12.3%。但锚杆间距的变化，也不会改变塑性应变、应力、位移的分布特征。由于位置靠下的锚杆在所受应力更大，因为建议在实际工程运用中下部锚杆采用施加预应力、增加锚杆直径、采用高性能锚杆等措施，进一步提高危岩的安全性，达到较好的经济合理性。

图13 2根锚杆不同间距的水平位移图

图14 2根锚杆不同间距的垂直位移图

3.3 3根锚杆不同间距参数危岩稳定性的有限元模拟

3.3.1 塑性应变结果分析

如图15所示，设置3根锚杆后的平均最大塑性应变值相比未设锚杆减小了77.5%，当锚杆间距为4.5 m时，最大塑性应变值分别相比间距2.5 m和间距3.5 m减小了7.0%和0.4%。这说明当锚杆间距越大时，其塑性应变的值越小。因此在施工设计时，考虑加大锚杆间距，有利于减小危岩后部与母岩间的塑性应变值，其安全稳定效果更好。

图15 3根锚杆不同间距的塑性应变值云图

3.3.2 应力结果分析

如图16所示，设置3根锚杆后应力将集中在锚杆下部，主要是在粘结危岩后部和母岩附近，边坡整体的应力都基本趋于一致，平均最大应力为2.498×104Pa。当锚杆间距过小为2.5 m时，锚杆的最大应力为别为间距3.5 m和4.5 m的1.26倍。因此考虑加大锚杆间距，有利于减小锚杆的应力。

3.3.3 位移结果分析

模型的水平位移云图如图17所示，相比未设置锚杆危岩最大水平位移为0.224 m，设置3根锚杆后危岩的最大平均水平位移为0.056 m减小了75.0%，锚杆间距为2.5 m的水平位移相比间距 3.5 m和4.5 m增大了5.1%和4.2%。因此可以认为锚杆间距对危岩的水平位移影响较小。

图16 3根锚杆不同间距的应力云图

图17 3根锚杆不同间距的水平位移云图

模型垂直位移云图如图18所示，相比未设置锚杆危岩最大垂直位移为0.261 m，设置3根锚杆后危岩的最大平均垂直位移为0.146 m减小了45.1%，锚杆间距为2.5 m的垂直位移相比间距 3.5 m和4.5 m增大了1.2%和0.6%。因此可以认为锚杆间距对危岩的垂直位移影响甚微。

图18 3根锚杆不同间距的垂直位移云图

综上所述，设置3根锚杆时，间距为3.5 m和4.5 m时危岩的安全性和防护效果非常接近，相比之下最大塑性应变值、最大应力、最大水平位移、最大垂直位移都相差甚微，分别占锚杆间距4.5 m结果的0.38%、-0.21%、-0.85%、-0.56%。以锚杆间距4.5 m为例，相比未设置锚杆，能够降低78.0%的最大塑性应变值、75.4%的水平位移、45.1%的垂直位移；且锚杆间距的变化，也不会改变塑性应变、应力、位移的分布特征。由于位置靠下的2根锚杆在所受应力更大，因而建议在实际工程运用中位置偏下的锚杆采用施加预应力、增加锚杆直径、采用高性能锚杆等措施提高其承载能力。

4 结 论

(1) 采用单根锚杆时，就有限元分析的结果的最大塑性应变值、最大应力、最大位移而言，在超过推测滑动面后不受锚杆长度变化影响，而锚杆入射角越小，对其控制效果越好。

(2) 在同一剖面上采用2根锚杆时，锚杆间距为2.5 m时对最大塑性应变值、最大应力、最大位移的控制效果最好；在同一剖面上采用3根锚杆时，锚杆间距为3.5 m和4.5 m对其控制效果基本一致。这说明为了缓解群锚效应，间距和锚杆的根数紧密相关，当采用锚杆数量较多时，可以适当扩大间距，能够有利于锚杆发挥其锚固力；而当间距过大时，锚固力在剖面上较为分散，也不利于安全性的控制。

(3) 同一剖面上位置偏下的锚杆受应力更大，这是由于位置偏下的锚杆受边坡危岩整体的重力和应力较大，因此在实际工程中应加大下部锚杆承受应力的能力。