带药缠绕复合壳体承压特性分析*

林天一,郑 庆,杨 明,江 真,王林祥

(上海航天动力技术研究所, 上海 201109)

0 引言

随着战术武器及相关技术的发展,导弹的轻质化、高性能越来越受到重视。固体火箭发动机作为导弹的动力来源,其推进性能的发挥直接影响到导弹的作战效能。以纤维缠绕复合壳体为代表的复合承压结构可实现发动机消极质量的大幅度下降,提高容积效率;同时可通过带药缠绕等形式实现药柱结构的多元化设计,提升发动机内弹道性能。对常规复合壳体的线性、非线性强度设计与分析国内已开展较多的研究工作[1-2],同时也建立了相应的复合壳体优化流程[3],开展了复合壳体承载力分析[4-6],但对于带药缠绕壳体由于芯模的特殊性,仍缺乏相应的研究。

纤维缠绕复合壳体承压性能与燃烧室工况及结构存在密切关系,复合壳体、药柱与绝热层三者材料性能与结构形式,对工作状态下壳体性能发挥有明显的作用,尤其是药柱芯模,在缠绕阶段由于纤维张力的存在使得芯模发生挤压收缩,导致壳体成型尺寸存在偏差。文中通过对带药缠绕复合壳体内压结构完整性分析,对比不同装药模量、肉厚条件下的复合壳体性能,为带药缠绕复合壳体的结构设计及工艺参数优化提供参考。

1 研究对象

文中所研究对象为带药缠绕固体火箭发动机燃烧室壳体,重点研究壳体在不同药柱条件下的结构承压特性,选用标准试验发动机,即壳体前后对称以保证柱段缠绕角恒定,其中药柱芯模外径Φ150 mm,根据网格分析方法开展壳体结构设计[7],纤维壳体壁厚1.62 mm,最大设计压强20 MPa,筒段铺层方案(±90°/±24°/+90°/±24°/±90°),筒段长度200 mm,药柱内孔直径Φ33 mm,其结构形式如图1所示,各材料物性参数如表1所示。

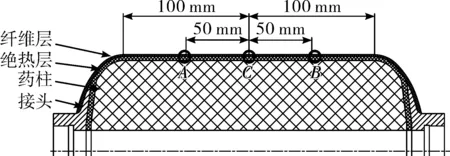
图1 带药缠绕复合壳体结构示意图

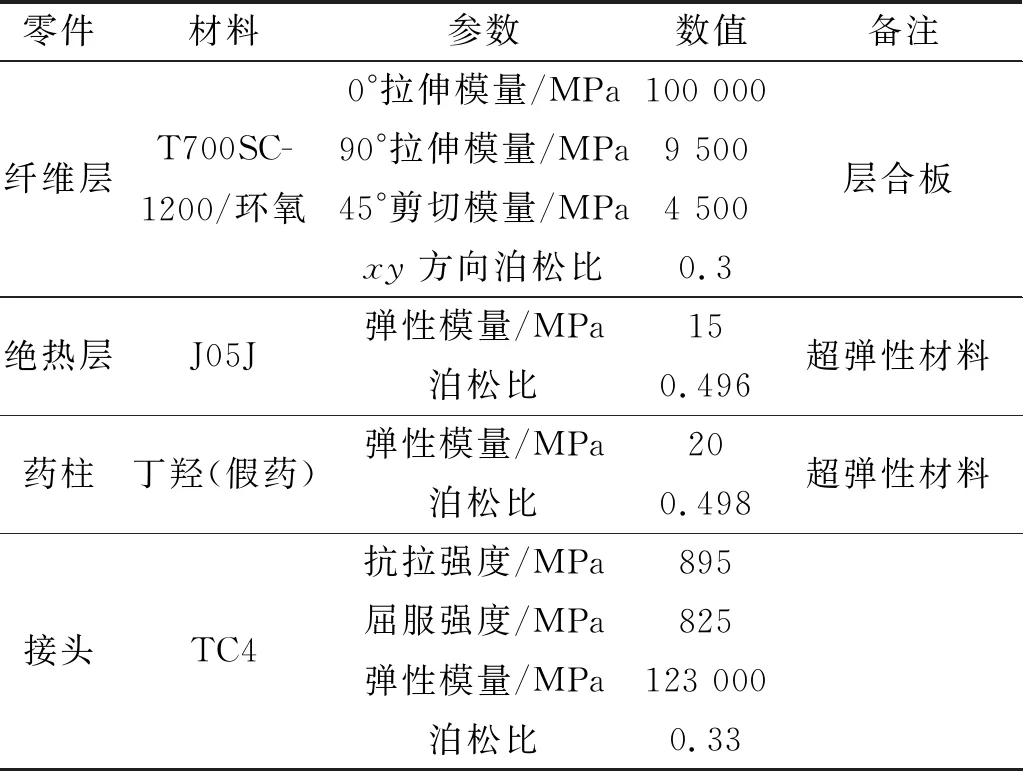
表1 材料力学性能

考虑到芯模制备的工艺可行性,实际制备按分体结构进行,该结构外形与图1设计方案保持一致。

2 结构完整性分析

2.1 仿真分析

为分析带药缠绕复合壳体结构完整性,进行以下假定:

1)不考虑各零件粘接面胶层厚度及层间相互作用;

2)绝热层与药柱均视为超弹性材料;

3)纤维层采用层合板理论进行有限元分析;

4)为避免对接面对壳体轴向的影响,仅考虑内压作用下筒段纤维层环向特性。

壳体最大设计压强为20 MPa,为避免极限载荷带来的壳体性能波动或损伤,选择5 MPa与10 MPa两个较低压强值用于仿真模型校验。仿真结果如表2与图2所示。

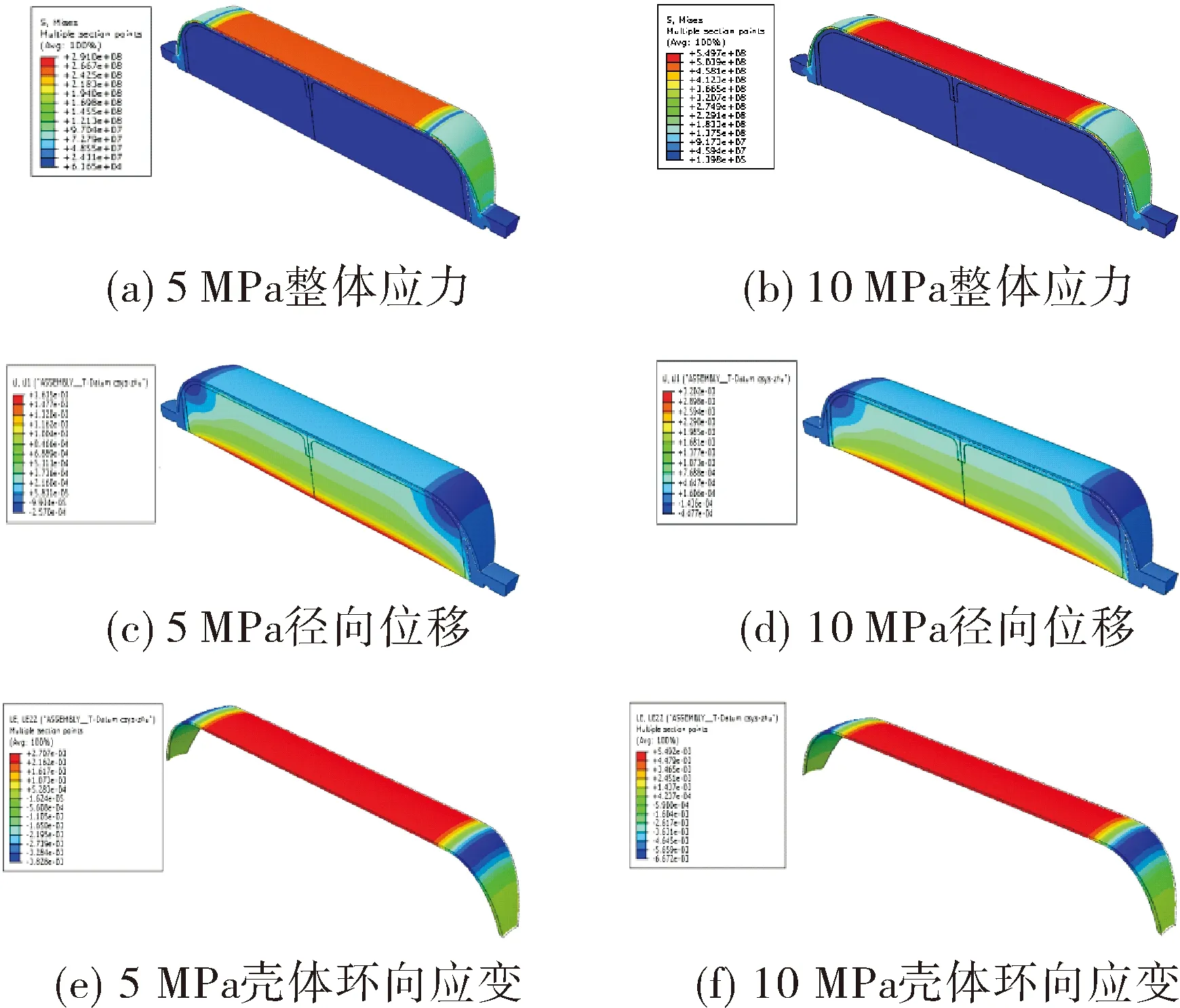
图2 结构完整性仿真结果

由仿真结果可见,带药缠绕复合壳体在5 MPa与10 MPa内压作用下结构完整无异常。

2.2 液压考核

对状态壳体选用假药进行制备(假药除无法燃烧外,其力学性能与真药一致),并对其进行液压试验考核,液压试验条件为:5 MPa条件下加载20 s,10 MPa条件下加载20 s,壳体无泄漏。同时对A点、B点进行应变数据采集,如图3所示。

图3 壳体制备与承压试验

壳体制备过程正常,壳体正常通过液压试验考核,无异常现象。共采集了A点、B点的0°、90°两个位置环向应变数据,如图4与表3所示。

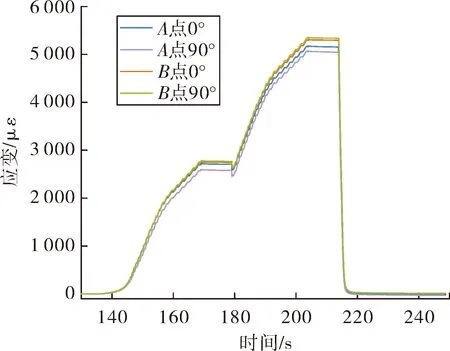
图4 特征点环向应变

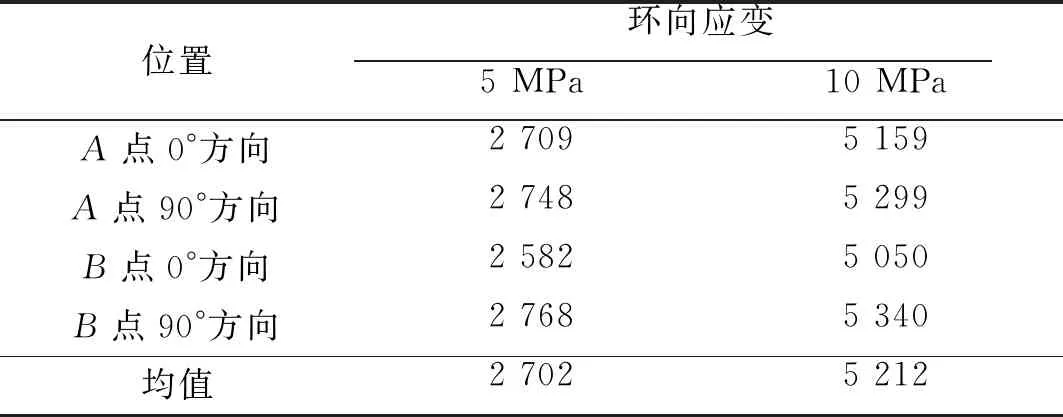
表3 应变测试结果 με

2.3 对比分析

由仿真及试验结果可见,5 MPa与10 MPa条件下特征点位置环向应变偏差仅为4.65%与2.94%。采用该静力学分析模式,应用上述假定通过有限元仿真形式,可较好表征带药缠绕复合壳体内压作用下的筒段壳体应变等分布情况。

3 纤维层承载特性分析

3.1 绝热层影响

图1对应模型绝热层设计厚度为3 mm,药柱与绝热层一体成型,绝热层的设计厚度主要与壳体热防护特性相关,为分析绝热层与药柱对壳体承载特性的影响,分别对纯纤维层、纤维层+绝热层、纤维层+绝热层+药柱进行10 MPa内压承载特性仿真。

仿真所用物性参数与表1一致,药柱厚度为55.5 mm。仿真结果如图5所示,以壳体左右对称点(C点)为基准,分别取C点左侧50 mm、右侧50 mm纤维层环向应变进行分析,如表4所示。

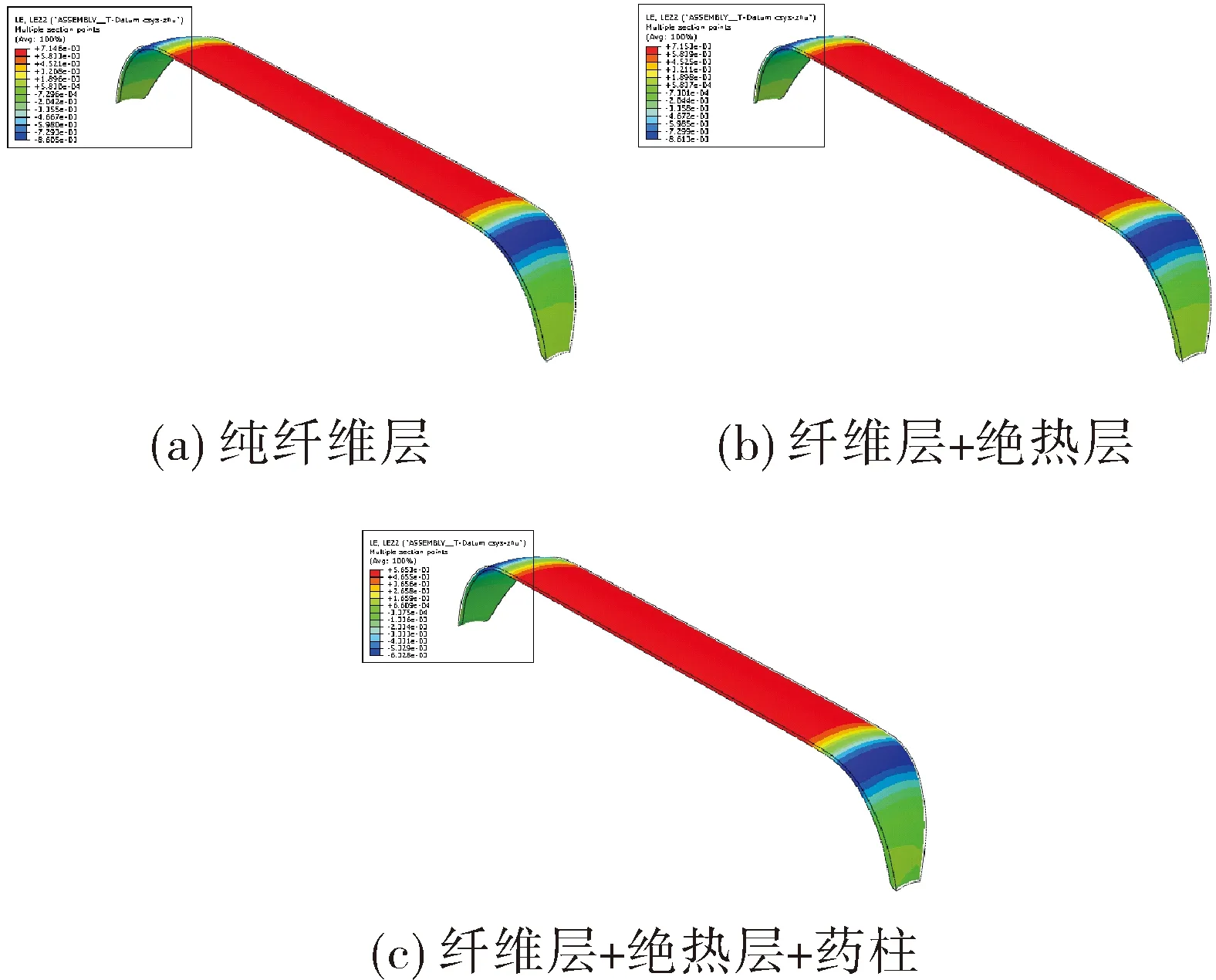
图5 纤维层壳体环向应变分布

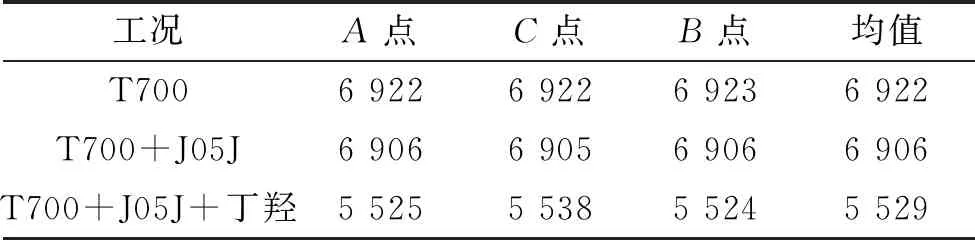
表4 筒段纤维层环向应变分布 με

由图5及表4可见,3 mm厚绝热层在10 MPa条件下对筒段纤维层环向应变仅产生约17 με(0.25%)的影响,而装药约产生1 377 με(24.9%)的影响,故可认为该状态绝热层对纤维层承载特性影响极小,可将其忽略,药柱对纤维层承载特性存在较大影响,环向应变减少可达24.9%。

3.2 药柱模量影响

为进一步分析药柱模量对纤维性能的发挥率影响,在上述有限元分析模型基础上对图1对应模型进行有限元仿真,在内压10 MPa、药柱肉厚55.5 mm条件下,仿真结果如表5与图6所示。

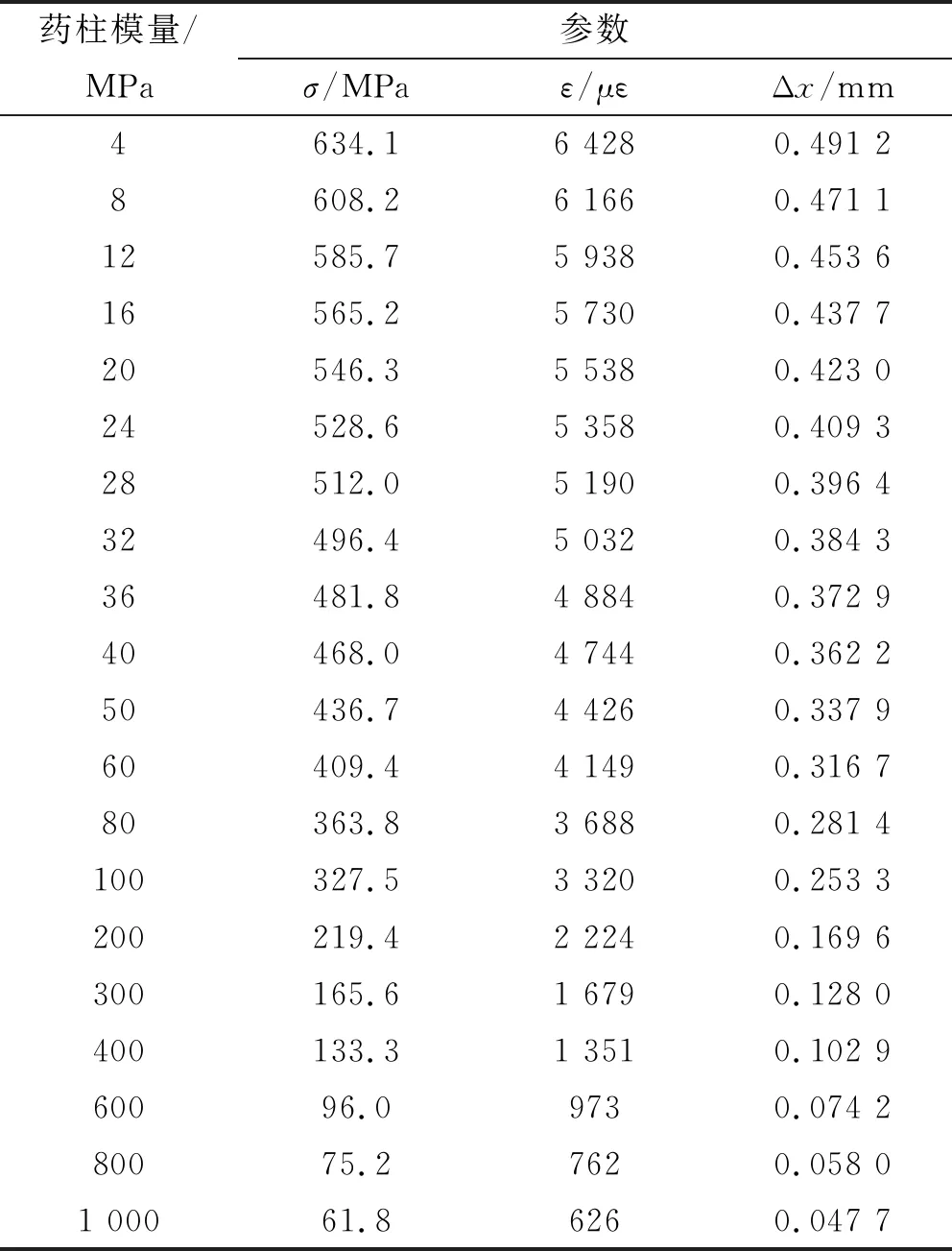
表5 C点(0 mm)位置不同药柱模量影响

由仿真结果分析可得纤维层中心处应力、环向应变及径向位移满足:

y=a(x1-b)c

(1)

壳体径向位移Δx与药柱模量E满足式(1)曲线变化规律,应力σ与环向应变ε均满足式(1)的规律,且与径向位移成比例关系。工程上药柱模量一般为5～30 MPa,故环向应力范围为504～628 MPa,应变范围为5 114～6 364 με,径向位移范围0.39～0.48 mm。同时,由表5与图6可知,当药柱模量超过400 MPa左右时,壳体环向应变与径向位移变化波动趋于平缓。

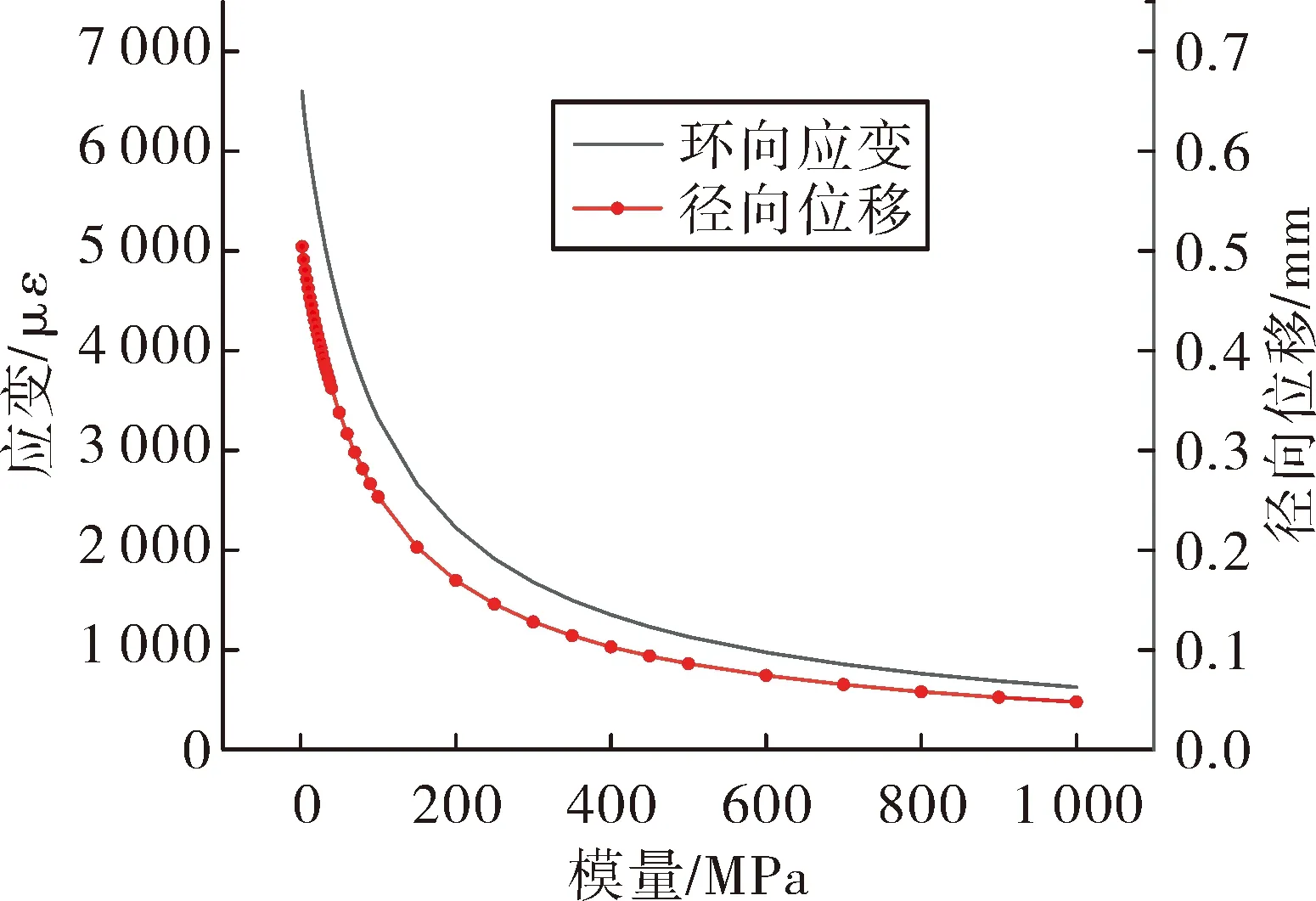
图6 不同药柱模量对应纤维层壳体环向应变与径向位移

3.3 药柱肉厚影响

为进一步分析药柱模量对纤维性能的发挥率影响,在上述有限元分析模型基础上对图1对应模型进行有限元仿真,在内压10 MPa、药柱模量20 MPa条件下,仿真结果如表7与图7所示。

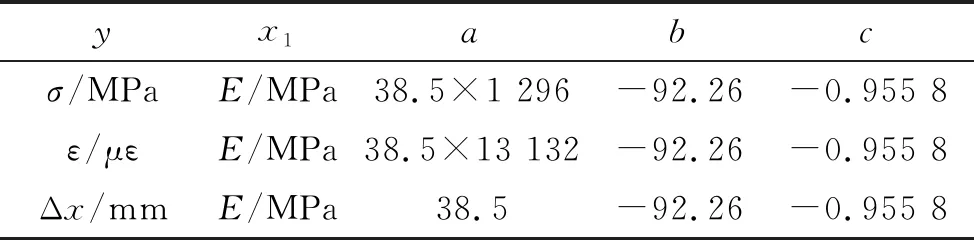
表6 参数(a,b,c)拟合结果

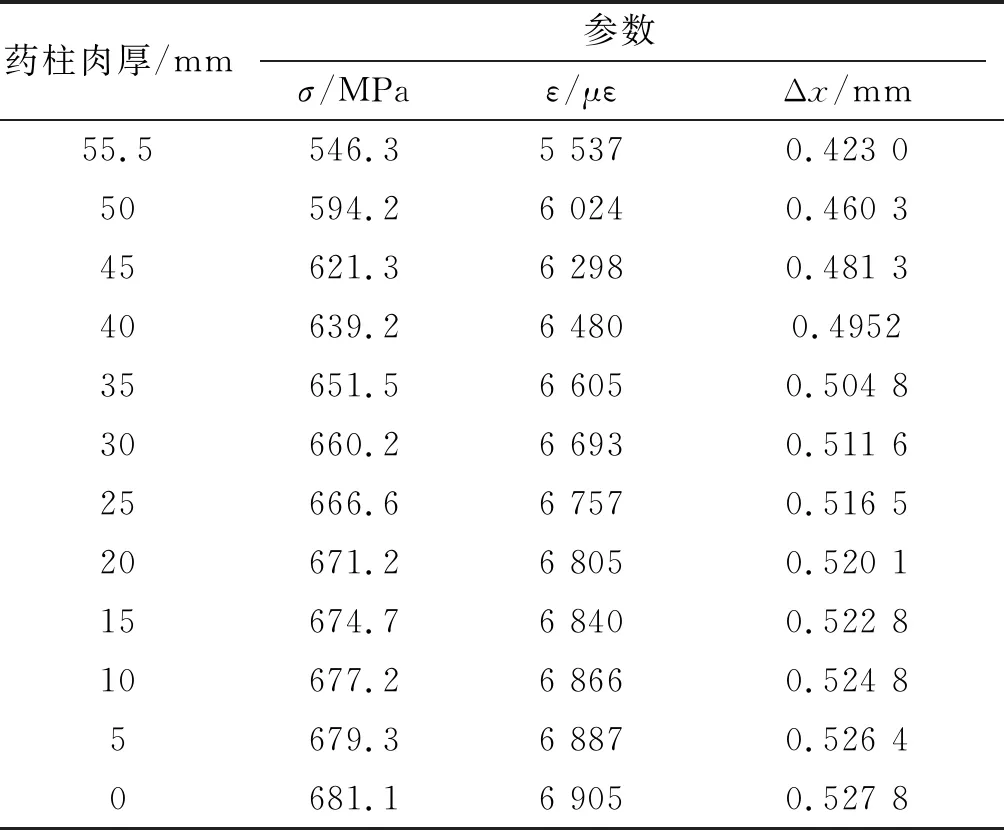
表7 C点(0 mm)位置不同药柱肉厚影响

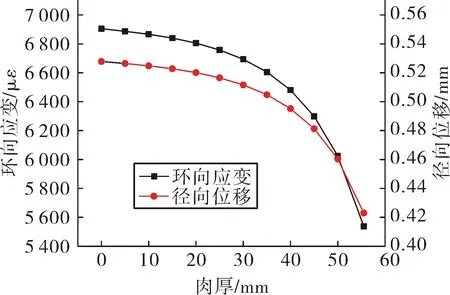
图7 不同药柱肉厚对应纤维层壳体环向应变与径向位移

由仿真结果分析可得纤维层中心处应力、环向应变及径向位移满足:

y=y0+AeR0x2

(2)

壳体Δx与药柱肉厚x满足指数型变化规律,σ与ε均满足此规律,且与Δx成比例关系。由表6与表8可见当纤维材料处于弹性区时,筒段σ数值上约为Δx的1 293倍,ε约为Δx的13 105倍,均呈现线性关系。对于采用药柱芯模的壳体在缠绕阶段可结合张力,平衡内压状态所产生的壳体径向位移。

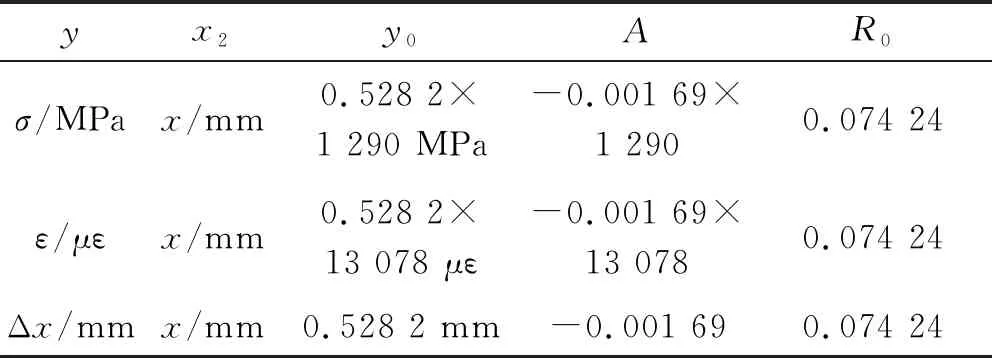
表8 参数(y0,A,R0)拟合结果

3.4 承压特性分析

实际工况条件下,对于内孔燃烧药柱,呈现增面燃烧效果,对于图1对应模型进行0维内弹道计算,所得Pc-t曲线如图8所示,最大压强10 MPa,工作时间3.26 s。由图4及表3可知,在壳体无破坏情况下,内压与壳体应变呈线性关系。故对于内孔型药柱,随着药面的燃烧,内压不断增大,当工作时间达3.1 s时达最大工作压强,此时筒段药柱剩余肉厚为3 mm,由式(2)可知此时C点应力为678.7 MPa,当工作时间超过3.1 s后内压下降,由式(2)可知此时C点最大应力未超过679 MPa。

对比图8所示Pc-t曲线,筒段壳体在大部分工作时间内工作压强均低于9 MPa,仅有约0.65 s左右超过 9 MPa,壳体径向位移仅在3.1 s附近达到极值,约为0.526 mm。

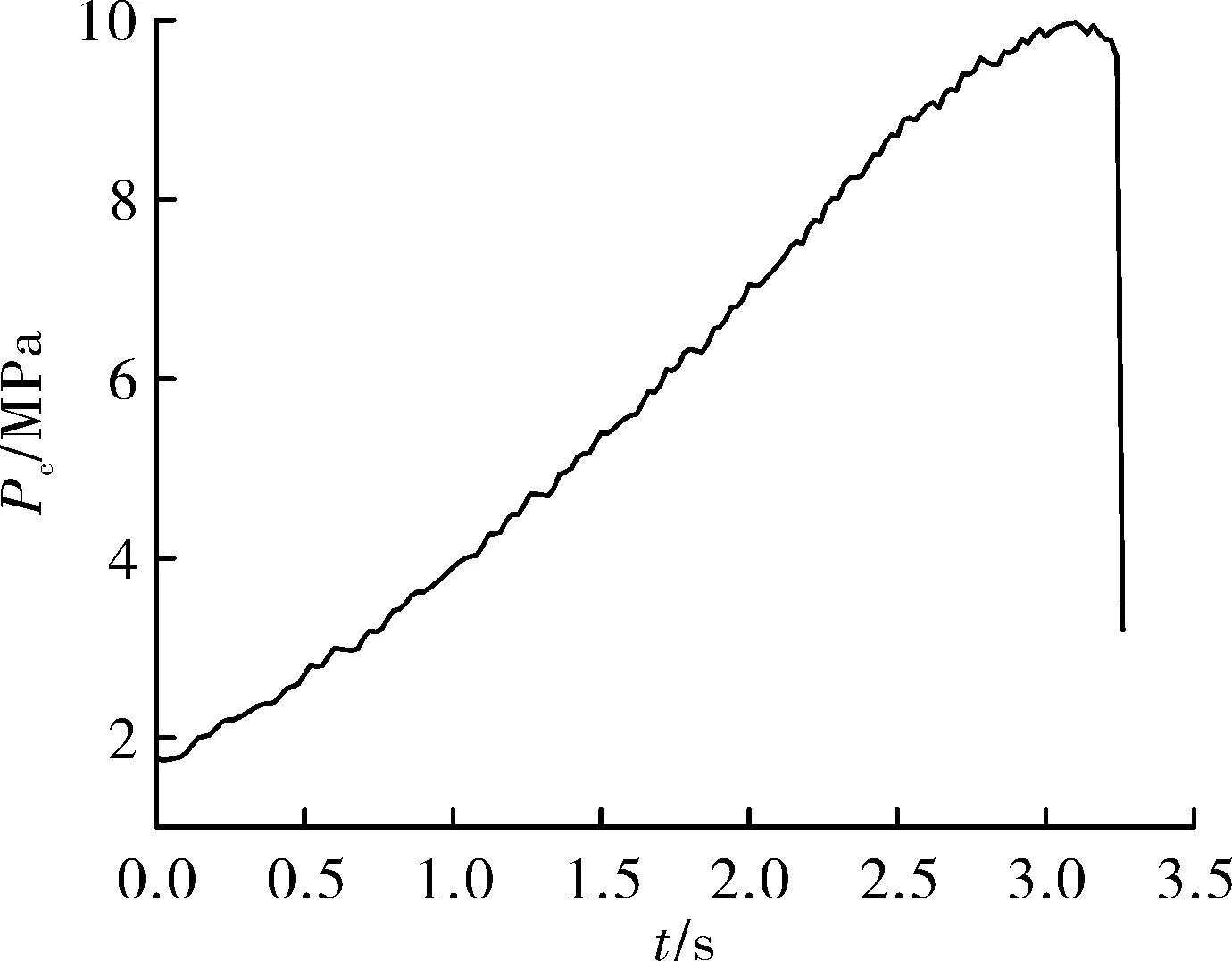
图8 Pc-t曲线

故可通过内弹道曲线,结合药柱结构特性,预示纤维层筒段应力、应变与变形,用于优化筒段纤维层厚度,减少壳体设计裕度,提高设计精准性。

此外,为保证发动机工作状态壳体最大外径,可采用弹性模量芯模,并结合张力制度适当增大各层缠绕张力,平衡壳体制造状态与工作状态的变形波动,以避免壳体变形引起的外径超差。

4 结论

根据标准试验发动机建立了纤维缠绕复合壳体静态内压承载结构完整性分析模型,可准确预示不同内压状态壳体的承载情况。

对药柱在不同模量与不同药柱肉厚条件下对纤维缠绕复合壳体承压特性的影响进行了详细分析,结果表明对于Φ150 mm直径带药缠绕复合壳体,绝热层在较薄条件下对筒段纤维层典型应变无明显作用;随着药柱模量的增加筒段纤维层应力、环向应变与径向位移减少呈现式(1)曲线变化规律,随着药柱厚度的减少筒段纤维层应力、环向应变与径向位移增加呈现指数型变化规律;σ数值上约为Δx的1 293倍,ε约为Δx的131 05倍,均呈现线性关系。

可通过内弹道曲线,结合药柱结构特性,预示纤维层筒段应力、应变与变形,用于优化筒段纤维层厚度,进一步减少壳体消极质量,提高设计精准性。同时,为保证发动机工作状态壳体最大外径,可采用高弹性芯模,结合张力制度适当增大各层缠绕张力,平衡壳体制造状态与工作状态的变形波动,以避免壳体变形引起的外径超差。