基于双目立体视觉的直升机旋翼桨叶位移变形测量方法
2020-03-29左承林岳廷瑞王勋年
左承林, 马 军,*, 岳廷瑞, 宋 晋, 王勋年
(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000; 2. 中国空气动力研究与发展中心 低速空气动力研究所, 四川 绵阳 621000)
0 引 言
旋翼是直升机最为核心的部件,直升机的飞行性能和飞行寿命都依赖于其结构设计、空气动力特性以及制造、试验与测试水平[1]。在诸多直升机故障中,旋翼系统故障最为常见,所占比例最高。因此,国内外均将优化直升机旋翼结构、提高旋翼空气动力特性作为直升机核心技术进行研究。旋翼桨叶高速旋转过程中的位移变形是反映旋翼系统运行性能的重要参数,对其进行精确测量是相关研究的关键。
传统方法通过在桨叶表面不同位置粘贴应变传感器来测量桨叶运动时所受到的力,根据桨叶材料特性或实际加载量,将受力变化转换为外形变化,基于不同应变传感器组成的不同桥路,计算得到桨叶的位移变形[2]。这种接触式测量方法的最大缺点在于粘贴的应变传感器破环了桨叶表面形状,从而不可避免地影响了桨叶气动外形,导致测量结果不够准确。此外,由于桨叶的尺寸限制以及旋转设备通道的有限利用度,可粘贴的应变传感器数量有限,无法安装于所有拟测量的桨叶剖面。
另一种接触式测量方法则以桨叶内部安装的光纤传感器测量其位移变形[3]。该方法是对上述表面贴片法的改进,光纤应变传感器在桨叶制造阶段就被埋入桨叶,可以在不影响桨叶外形和结构强度的情况下进行测量。但该方法同样存在测量点数少、精细度较差等缺点,且内埋光纤传感器桨叶的制造难度和成本都非常高。
随着视觉测量技术的快速发展,基于立体视觉原理的测量方法逐渐被应用于直升机旋翼桨叶位移变形测量。该方法能够对旋翼桨叶的位移变形进行非接触式测量,操作简单,易于维护,对环境要求也较低。2001年,德国宇航中心携手法国航空航天研究院、美国国家航空航天局兰利研究中心以及美国陆军航空飞行动力学学会,在德荷DNW LLF风洞开展了HART II试验,首次采用立体视觉方法对缩比40%、半径2 m的BO-105桨叶模型的位移变形参数进行了测量[4-6]。在2008年的SMART试验中,采用立体视觉方法成功测量了桨叶(长17 ft)在前飞速度228 km/h、旋转频率6.5 Hz条件下、90°旋转范围内的位移变形参数[7]。在2009年的IBC试验中,立体视觉方法得到进一步发展,研究者使用4台相机测量了全尺寸UH-60A旋翼桨叶在180°旋转范围内的位移变形[8];其后的改进试验中,使用8台相机实现了360°旋转范围内的测量[9-13]。此外,数字图像相关方法也被应用于直升机旋翼桨叶位移变形测量,该方法通过在桨叶表面投射或喷涂随机散斑图案,能够实现桨叶位移变形的整体连续测量[14-18]。
南昌航空大学熊邦书课题组[19-23]开展了大量基于立体视觉的旋翼桨叶运动变形参数测量方法研究,但对测量对象和测量环境进行了极大简化,也未实际应用于风洞试验。吴国宝等[24]提出了一种基于三维数字影像的非接触式测量方法,实现了旋翼桨叶运动参数的有效测量。韩涛等[25]构建了一种随旋翼旋转的立体相机系统,实现了旋翼桨叶的三维动态变形测量。
针对直升机风洞试验中旋翼桨叶高速旋转状态下的位移变形测量需求,本文提出一种基于双目立体视觉原理的三维测量方法。首先,采用编码标记方法,在旋翼桨叶上布置具有唯一编码信息的标记点,解决三维测量中旋翼桨叶特征不明显的问题;然后,以高频激光器提供纳秒级脉冲照明,同步触发高速CCD相机采集图像数据,实现高速旋转状态下旋翼桨叶瞬态图像对的清晰获取;再对采集的图像对中的标记点进行检测和解码识别,根据其唯一码值实现精准匹配;最后,基于双目立体视觉原理,计算标记点的三维坐标,进而计算得到旋翼桨叶的位移变形参数。
1 双目成像系统
在直升机风洞试验中,旋翼桨叶处于高速旋转状态,工况复杂使得测量难以进行。以直径2 m的旋翼为例,其额定转速为2100 r/min,桨尖线速度高达220 m/s,普通成像设备很难拍摄到清晰的旋翼桨叶瞬态图像,无法实现桨叶位移变形参数的精确测量。为此,本文基于高频激光器和高速CCD相机,构建了适用于直升机风洞试验测量的双目成像系统,如图1所示。
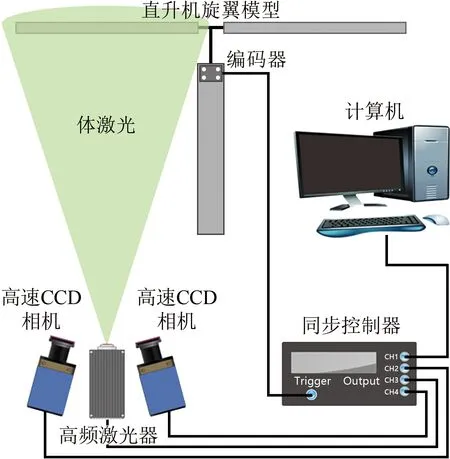
图1 双目成像系统结构
在双目成像系统中,2台高速CCD相机布置于旋翼桨叶下方,其成像视场覆盖桨叶旋转范围的一个象限;高频激光器通过激光扩束镜形成体激光,为测量区域提供纳秒级瞬态照明;同步控制器对高速CCD相机和高频激光器进行时钟同步,并根据旋翼编码器信号触发高速CCD相机同步采集旋翼桨叶图像。
瞬态成像原理如图2所示。基于同步控制器,相机与激光器被调至相同频率。在相对较长的相机曝光时间内,激光器仅进行极短时间的脉冲照明,以使旋翼桨叶在相机CCD上成像;而在相机曝光时间内的非照明时段,由于无光源照明,旋翼桨叶不会在相机CCD上成像,即:相机真正有效的曝光时间就是激光器的脉冲照明时间,因而可以拍摄得到高速旋转状态下清晰无拖尾的桨叶瞬态图像。
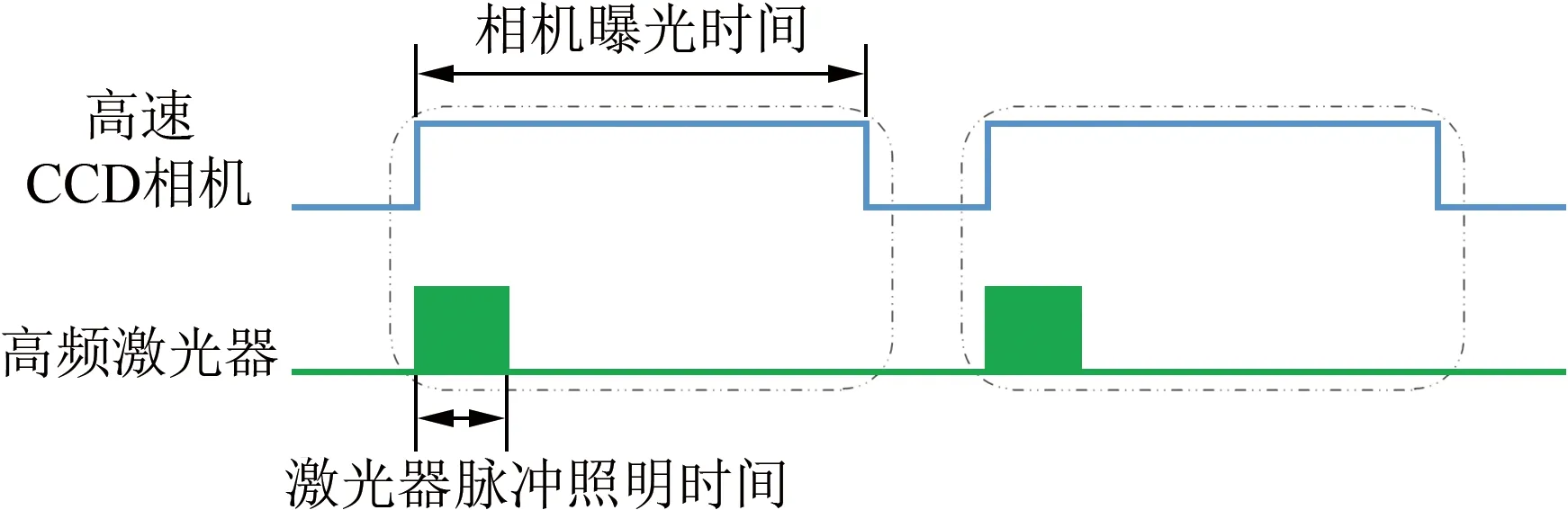
图2 瞬态成像原理
2 双目立体标定
双目立体视觉原理如图3所示。基于视差原理,采用2台相机从不同位置获取被测物体的2幅图像,通过计算图像中对应点的位置偏差,可得到物体三维信息。

图3 双目立体视觉原理
双目立体标定即是求解双目成像系统的内外参数,建立双目视觉测量与三维世界测量之间的对应关系。目前,典型的标定方法主要有直接线形变换法[26]、RAC两步法[27]和张正友标定法[28]。其中,张正友标定法利用不同视角位置的平面标定板上特征点的世界坐标与其图像上像点坐标之间的对应关系进行标定,具有使用简单、标定精度高等优点。因此,本文采用张正友标定法进行标定,并对拍摄图像进行非线性畸变修正。
首先,分别对2台相机的内外参数进行标定。对于三维空间中的任意一点P,通常采用理想的针孔成像模型描述其在相机成像平面上的投影:
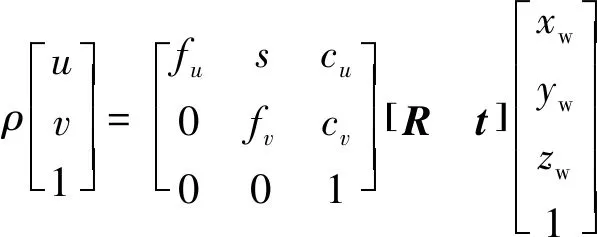
(1)
式中,ρ为比例因子;(xw,yw,zw)表示空间点P在世界坐标系OwXwYwZw下的三维坐标;(u,v)表示空间点P的投影点在图像坐标系ouv下的二维坐标;fu、fv表示相机在u轴和v轴方向上的等效焦距;(cu,cv)表示相机的光学中心坐标;s表示u轴和v轴的不垂直因子,通常情况下s=0;R和t表示世界坐标系OwXwYwZw变换到相机坐标系OXYZ的3×3旋转矩阵和3×1平移矢量。R和t是相机的外部参数,描述了世界坐标系到相机坐标系间的变换关系,令A为相机内部参数:

(2)
设标定板平面位于世界坐标系Zw=0平面上,则标定板上所有特征点的世界坐标zw=0,式(1)可简化为:
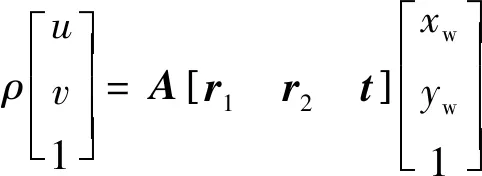
(3)
式中,ri(i=1, 2)表示旋转矩阵R的第i列。令H=A[r1r2t]作为单应矩阵,设:
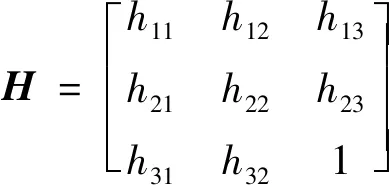
(4)
将H记为[h1h2h3],则有:
[h1h2h3]=λA[r1r2t]
(5)
式中,λ为任意非零常数因子。由于旋转矩阵具有单位正交性,可以得到内参矩阵的基本约束如下:

(6)
进一步地,设:
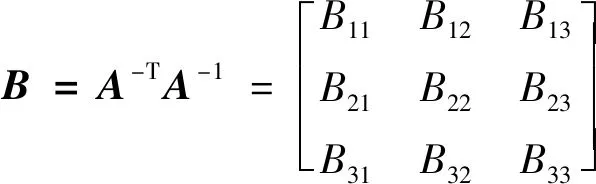
(7)
由于B是一个对称矩阵,可定义六维向量b=[B11B12B22B13B23B33],则有:
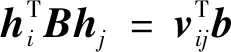
(8)
其中,
vij=[hi1hj1hi1hj2+hi2hj2hi2hj2
hi3hj1+hi1hj3hi3hj2+hi2hj3hi3hj3]T
(9)
根据式(6)的约束条件,可得到关于向量b的2个齐次方程:
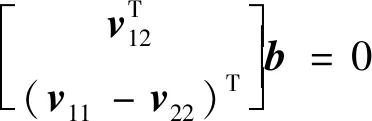
(10)
拍摄获取标定板不同位置的n副图像,就可得到2n个方程,记为:
Vb=0
(11)
式中,V是一个2n×6的矩阵,b有6个未知数,当n≥3时,就可得到b的带比例因子的唯一解。求得b后即可得到矩阵B,进而求得相机的内部参数:

(12)
进一步地,可求解相机的外部参数:

(13)
在实际应用中,相机镜头并非理想的光学镜头,得到的图像不可避免地会存在一定程度的畸变,其中最主要的就是径向畸变,需采用径向畸变模型对其进行校正:

(14)
式中,(ud,vd)和(u,v)分别表示实际情况(有畸变)和理想情况下(无畸变)的图像坐标,k1、k2为径向畸变系数。给定n幅标定图像,采用最小二乘法即可求出径向畸变系数k1和k2的初始估计。
上述方法计算出的相机内外参数初值易受噪声干扰,需采用最大似然估计对参数进行优化。设n幅图像中m×n个角点都存在独立同分布的噪声,给定目标函数如下:
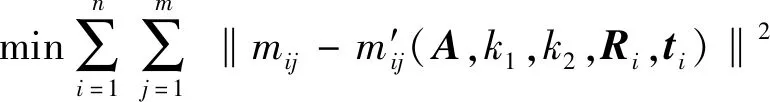
(15)
式中,mij和m′ij(A,k1,k2,Ri,ti)分别表示第i幅图像中第j个角点的图像坐标和投影点坐标;Ri和ti分别表示第i幅图像所对应的旋转矩阵和平移向量。式(15)是一个非线性优化问题,可以利用稳定性很好的LM(Levenberg-Marquardt)优化算法进行求解,从而得到优化后的相机内外参数。
对左右相机的内外参数进行标定后,即可确定它们之间的相对位姿,即双目成像系统的外参数。令Rr2l、tr2l表示从右相机坐标系到左相机坐标系的旋转矩阵和平移向量,则有如下关系:
Xl=Rr2lXr+tr2l
(16)
式中,Xl和Xr分别表示三维空间点P在左右相机坐标系下的三维坐标。基于标定求得的左右相机的外参数,可计算得到双目成像系统的外参数:
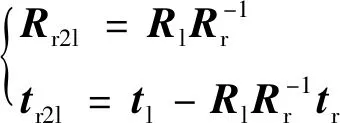
(17)
3 标记点检测识别
双目测量时,由于旋翼桨叶表面没有显著的纹理特征,传统立体匹配方法无法实现桨叶图像对的精确匹配。本文采用编码标记方法,在桨叶表面布置具有唯一编码信息的标记点,通过检测和解码识别,可实现标记点的精确定位和匹配。
如图4(a)所示,编码标记点由中间目标圆和外缘编码环构成,目标圆中心点用于定位,编码环用于编码。编码环按角度等分为8份,根据黑白颜色分别对应一个二进制位“0”或“1”,则整个编码环对应于一个8位的二进制码值,如图4(b)所示。由于解码方向及起始位置不同,同一编码标记点存在不同的二进制码值。为确保码值的唯一性,按逆时针方向逐个变换解码起始位置,可得到8个二进制码值及其对应的十进制数,以其中最小的十进制数作为编码标记点的唯一码值。当然,为获得更多类型的编码标记点,可对编码环进行更多数量的等分。
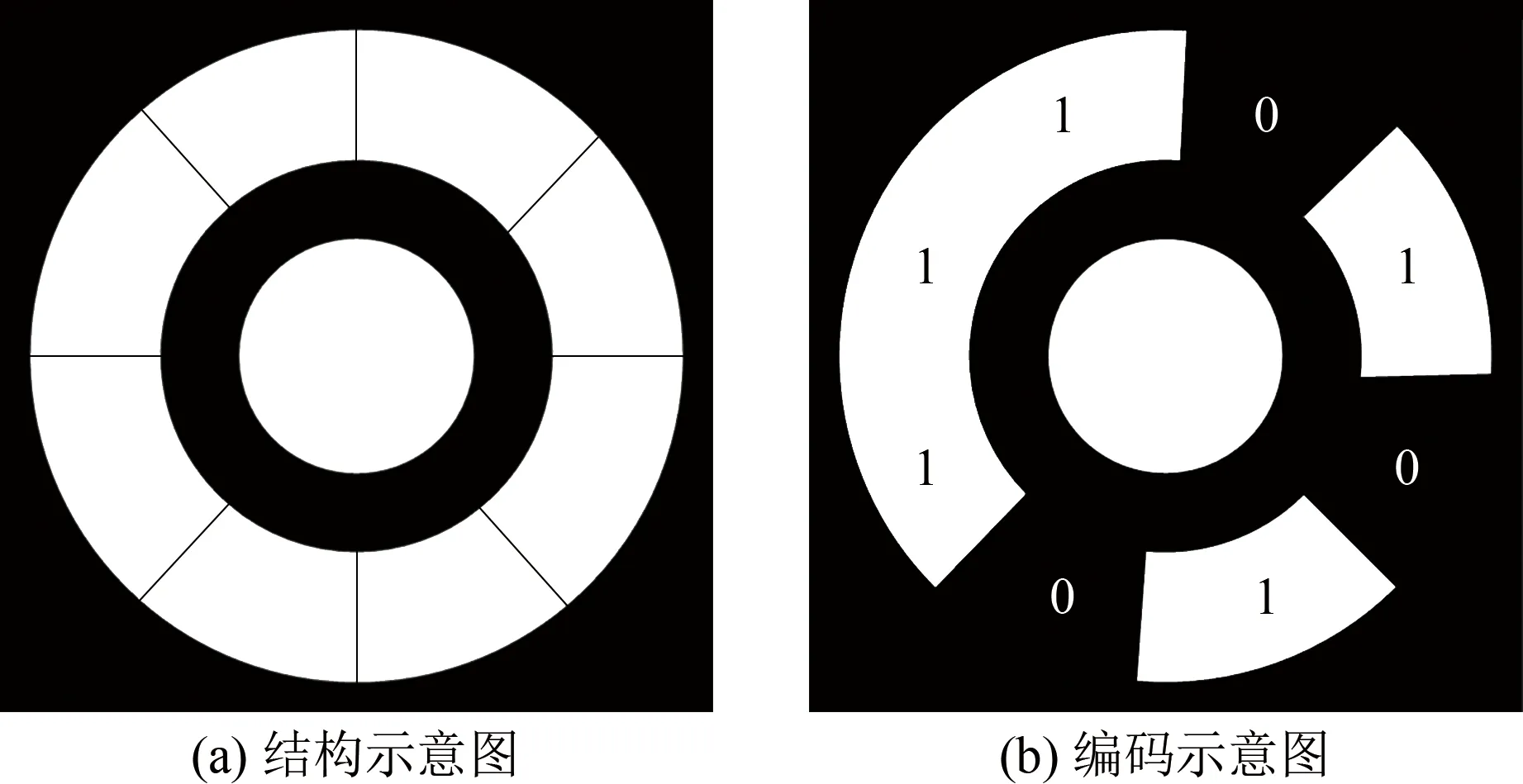
图4 编码标记点
3.1 检测定位
首先采用最大类间方差法(OTSU)对旋翼桨叶图像进行自适应阈值分割,将编码标记点分离出来,如图5(a)所示;然后,采用Canny算子进行边缘检测,提取得到编码标记点的像素级边缘轮廓,如图5(b)所示;再计算各边缘轮廓的周长L、面积S以及形状因子G=L2/(4πS),通过设置合适的阈值,筛除编码标记点的编码环轮廓,仅保留目标圆轮廓,如图5(c)所示。为获得亚像素级定位精度,在像素级边缘检测结果的基础上,采用Zernike正交矩法对编码标记点目标圆提取得到亚像素级边缘。

图5 标记点边缘检测
由于拍摄角度的影响,编码标记点的成像目标圆为椭圆。为定位其中心点,需进行椭圆拟合。对于任意椭圆,其一般方程为:
f(x,y)=x2+Axy+By2+Cx+Dy+E=0
(18)
对检测得到的成像目标圆的亚像素级边缘进行最小二乘椭圆拟合,即可解算得到椭圆方程参数A、B、C、D、E,进而计算得到:

(19)
式中,(x0,y0)、a、b、θ分别表示成像目标圆的中心坐标、半长轴、半短轴以及姿态角。基于成像目标圆的中心坐标,即可实现编码标记点的精确定位。3.2 解码识别
编码标记点成像符合仿射变换,因此,成像目标圆与成像编码环中心重合,姿态角相同,且大小比例保持不变。根据编码标记点的物理尺寸以及成像目标圆的椭圆参数,可计算得到成像编码环的椭圆参数:
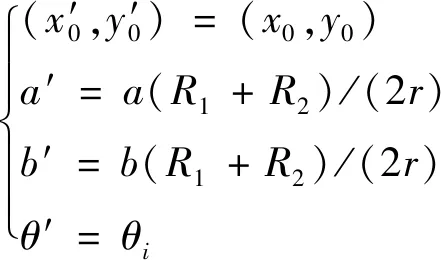
(20)
式中,R1和R2分别表示编码环的物理内环半径和物理外环半径,r表示目标圆的物理半径。
基于成像编码环的椭圆参数,在成像编码环上进行360°采样,如图6所示。通过分析确定采样序列的码值,即可实现编码标记点的解码识别。进一步地,根据桨叶图像对中编码标记点的解码值,即可实现其精确匹配。
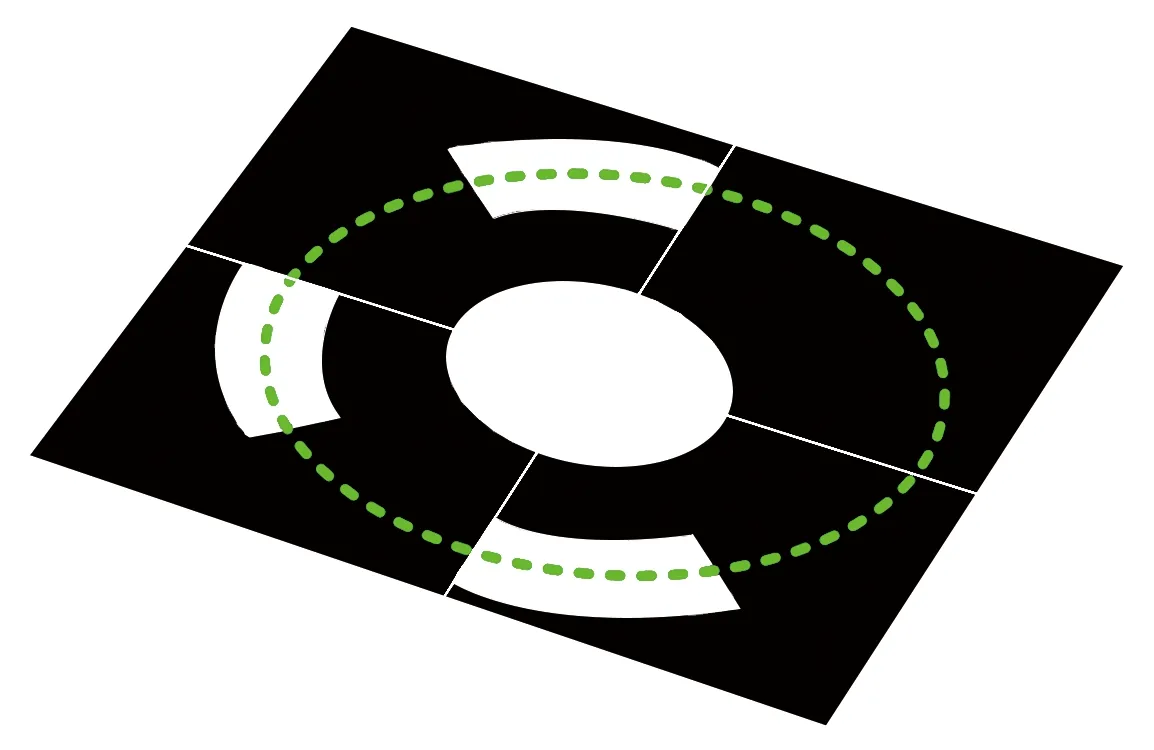
图6 编码环采样
3.3 三维坐标计算
在获得桨叶图像对中相匹配标记点的二维图像坐标后,即可根据双目立体标定得到的内外参数,计算标记点的三维空间坐标。设旋翼桨叶上某一标记点的三维空间坐标为(x,y,z),其在图像对中的二维图像坐标分别为(ul,vl)、(ur,vr),存在如下关系:

(21)
联立上式将ρl和ρr消去,可得到4个关于x、y、z的线性方程,采用最小二乘法即可求得三维坐标值。
4 试验结果与分析
在中国空气动力研究与发展中心Φ3.2 m风洞的Φ2 m刚性旋翼试验台上开展了验证试验,如图7所示。试验中,双目成像系统安装固定于旋翼下方的测量平台上,确保测量时相机不会发生振动。2台相机的夹角约为30°,距离旋翼桨叶约2.5 m,测量视场约为1 m×1 m,覆盖了旋翼桨叶90°旋转范围。2台高速CCD相机分辨率均为1024 pixel×1024 pixel,最大帧频3.6 kHz,动态范围12 bit。高频激光器波长527 nm,能量2×30 mJ@1 kHz,脉冲宽度150 ns。对悬停工况下的桨叶位移变形参数进行了测量,试验工况包括:转速400、1300和1860 r/min,控制总距0°、6°、10°。

图7 Φ2 m刚性旋翼试验台验证试验
图8为1860 r/min转速下双目成像系统拍摄的旋翼桨叶6个方位角处的合成图像,桨叶表面的编码标记点都清晰可见,无拖尾模糊现象,验证了双目成像系统对高速旋转桨叶进行瞬态成像的可行性。

图8 旋翼桨叶合成图像
首先,采用张正友标定法对双目成像系统的内外参数进行标定。图9为双目立体标定使用的棋盘格标定板,以氧化铝材料制成,尺寸大小为660 mm×500 mm,加工精度±0.01 mm,可满足1 m×1 m测量视场的高精度标定。标定板绘有15×11个黑白相间的格子,每个格子的大小为40 mm×40 mm。试验中,采用悬吊方式将标定板置于测量视场内,通过改变标定板位置和倾角,拍摄获得不同的标定图像,进而解算出双目成像系统的内外参数,如表1~3所示。
然后,对拍摄获得的桨叶图像中的编码标记点进行检测识别和三维坐标计算。图10为转速1860 r/min、控制总距0°、6°、10°工况下的编码标记点检测识别结果。可以看到,高转速和控制总距变化并不会影响编码标记点检测识别的准确性。图11为图10中编码标记点的三维坐标计算结果。
旋翼桨叶沿展向共有10对编码标记点,每对编码标记点之间的物理距离均为35 mm。在不同转速和控制总距下,基于测得的所有方位角位置的编码标记点对之间的三维空间距离,计算测量精度σ1和准度σ2:

图9 棋盘格标定板

表1 左相机内部参数标定结果Table 1 Internal calibration results of the left camera

表2 右相机内部参数标定结果Table 2 Internal calibration results of the right camera

表3 双目成像系统外部参数标定结果Table 3 External calibration results of the binocular imaging system

图10 编码标记点检测识别结果
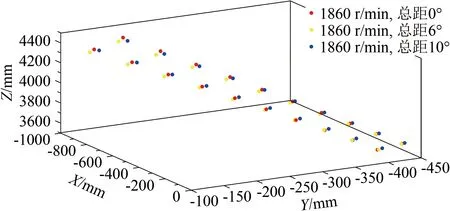
图11 编码标记点三维坐标计算结果
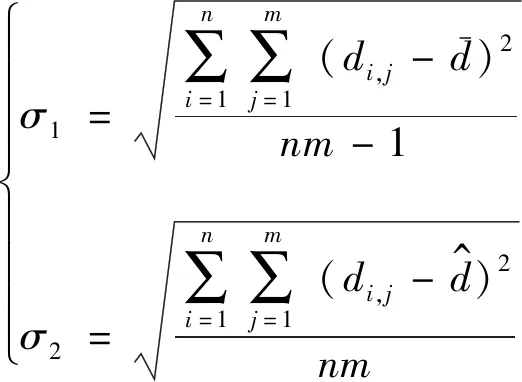
(22)

表4为不同转速和控制总距条件下计算得到的测量精准度。可以看到,随着控制总距增大,测量精准度逐渐降低,这是因为双目视觉在相机坐标系Z轴方向上的误差通常较大,控制总距增大使得编码标记点对在该方向上的距离偏差增大,导致测量精准度降低。此外,转速越大,桨叶发生的位移变形就越大,因此,转速增大也会使测量精准度降低。

表4 测量精准度Table 4 Measuring accuracy
基于编码标记点三维坐标,对旋翼桨叶进行动态三维重构。图12(a)为控制总距0°时转速400、1300和1860 r/min条件下的重构结果。可以看到,随着转速增加,旋翼桨叶在离心力作用下逐渐拉平,桨尖高度降低。图12(b)和(c)分别为转速1300和1860 r/min时控制总距0°、6°、10°条件下的重构结果。可以看到,随着控制总距增大,旋翼桨叶在气动载荷作用下逐渐抬高,桨尖上翘。
进一步地,基于桨尖编码标记点三维坐标,计算不同转速和控制总距条件下的桨尖挥舞位移量。如图13所示,在相同转速下,控制总距越大,桨尖挥舞位移量越大;而转速越大,控制总距增加带来的挥舞位移增量就越大。此外,由于旋翼处于悬停状态,不同转速和控制总距条件下的桨尖挥舞位移量基本保持稳定,其平均挥舞位移量如表5所示。



图12 旋翼桨叶动态三维重构结果
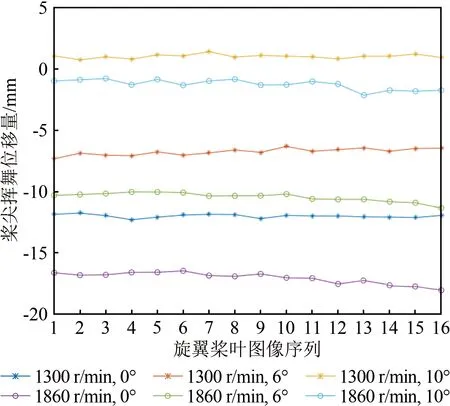
图13 桨尖挥舞位移量

表5 桨尖平均挥舞位移量Table 5 Average displacements of the blade tip
图14和15为不同转速和控制总距条件下的桨根、桨尖总距变化曲线,其平均值如表6所示。可以看到:当控制总距0°时,桨叶本身就存在一定的偏转角度,且桨尖位置的偏转角度明显更大,这与试验使用桨叶的结构相吻合;当控制总距相同时,不同转速条件下桨根和桨尖的总距都只存在较小差异,这与桨叶的刚性特性相吻合。

图14 桨根总距变化
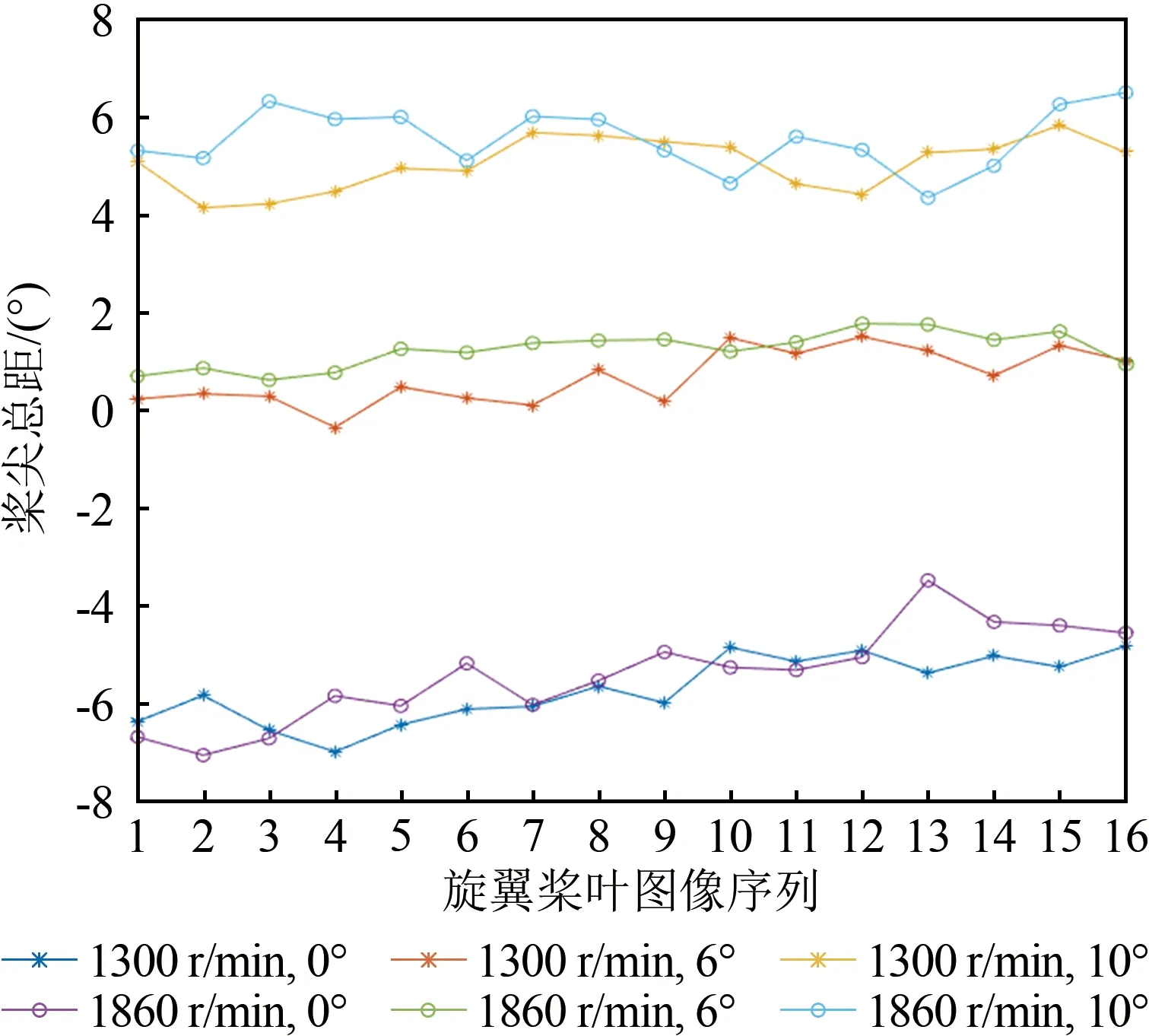
图15 桨尖总距变化
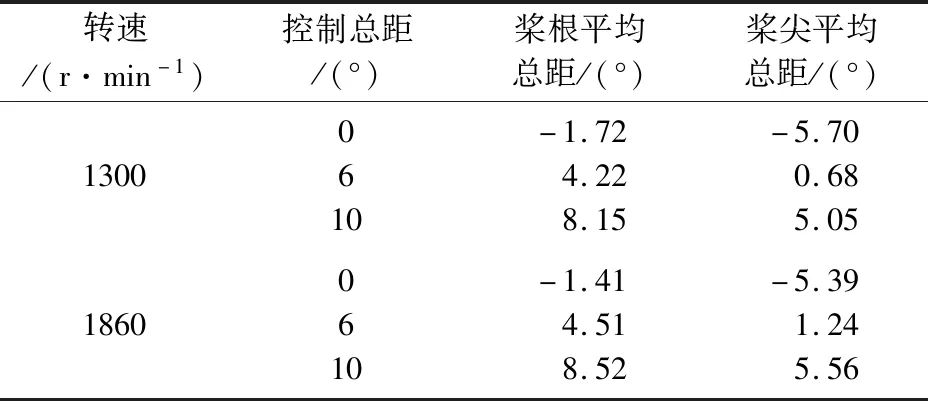
表6 桨根、桨尖平均总距Table 6 Average pitch angle of the blade root and tip
表7为不同转速和控制总距条件下桨根和桨尖的总距变化量。可以看到,桨根位置的总距变化量与控制总距最为吻合,桨尖位置因受到更大的气动载荷作用,其总距变化偏差相对较大。
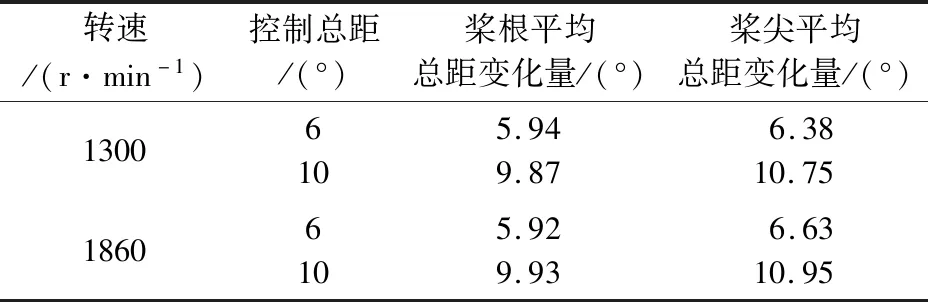
表7 桨根、桨尖总距变化量Table 7 Changes on pitch angle of the blade root and tip
5 结 论
本文提出了一种基于双目立体视觉的三维测量方法,实现了旋翼桨叶高速旋转状态下的位移变形测量。结果表明:该方法测量精度小于0.1 mm,测量准度小于0.3 mm,能够满足直升机旋翼桨叶位移变形的高精度测量需求。
