宽行加工中行宽与主曲率的关系研究

贾英杰，陈志同

（北京航空航天大学机械工程及自动化学院，北京 100191）

1 引言

在曲面加工中，宽行加工是有效提高加工效率的一种方法，通过优化刀具的姿态实现加工行宽的最大化[1]。中点法[2]可以实现刀具与曲面间的双点切触，获得较大行宽，是目前宽行加工中常用的刀位优化算法。但由于中点法在刀位优化过程中需要调整两个以上的设计变量，若逐一优化每个刀位，不仅需要耗费大量计算时间，而且生成的刀轨容易出现波动。

一行刀轨的行宽取决于每行刀轨的最窄行宽点，而对于行宽较大处，实际上没有必要以行宽最大化为目标对刀具姿态做充分优化。如果只优化计算最窄行宽处的刀位，其他刀位通过插值得到，这样既节约了计算时间，又可以有效解决刀轨不光顺问题。其中关键的一步，便是最窄行宽点的预测，这也是研究目的和意义所在。目前还没有对关于曲面上最窄行宽点的位置的相关研究，可以参考的现有文献中求解加工行宽的方法有很多。基于微分几何的投影椭圆法[3-4]计算简单，但仅仅在单一平面内衡量刀具和工件曲面的接触情况，误差较大。北航基于最短距离线原理，发展出了离散刀具法[5-7]和离散工件曲面法[8]。通过建立任意刀位下的误差分布曲线，进而确定加工行宽。这种基于数值求解的方法可以精确计算出加工行宽，基于离散刀具法研究行宽与曲率的关系。

首先对误差分布和曲率的关系进行理论研究，然后使用实验方法对中点法下行宽和主曲率的关系进行研究，最后给出了依据主曲率预判最窄行宽位置的方法。

2 误差分布与曲率关系研究

基于最短距离线对的误差分布曲线求解示意图，如图1所示。

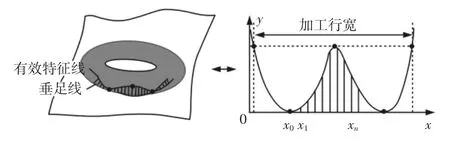
图1 误差分布求解示意图Fig.1 Error Distribution Solution

设误差分布曲线为函数y=f（x），其中一个切触点为x=x0，则f（x0）=0，f′（x0）=0。依次在x=x0，x1，…，xn-1处进行泰勒展开如下：

忽略无穷小项，并x=xi+1将带入上式，令yi=f（xi），驻yi=yi+1-yi，得到：

则x=xn处的最短距离线的长度yn为：

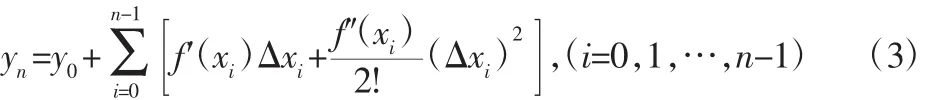
其中，驻xi表示的离散密度趋于无穷小且已知，因此yn可以写成关于f′（xi）和f″（xi）的函数，即：

二阶导数可以通过一阶导数的差分得到：

又有曲率的计算公式如下：

联立式、为方程组，求解f′（xi）、f″（xi）和ρi的关系。设其中ρi（i＝0，1，…，n）设为已知量，f′（x0）=0为已知，f′（xi），（i＝0，1，…，n）和f″（xi），（i＝0，1，…，n）为未知量。该方程组中未知量的个数和方程的个数相等均为2n+1，方程组可解。因此f′（xi）和f″（xi）可以写成关于ρi的函数：

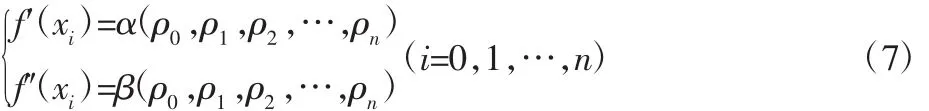
将式带入式，得到yn关于ρi的函数：

由式可以得出，误差分布曲线的形状由其曲率分布决定，而式中的曲率ρ由刀具曲面与设计曲面的曲率共同决定的[10]。将上述结论扩展到空间中，可以得出误差分布是由刀具曲率和设计曲面的局部曲率分布决定的。

行宽是基于误差分布曲线进行计算的，此外还需要设定残留高度。因此可以认为行宽是以设计曲面的局部曲率分布、刀具半径和残留高度为变量的函数，实际加工过程中残留高度和刀具半径是确定的，因此设计曲面的局部曲率分布决定了行宽。因此研究行宽与曲率的关系就可以找到预测最窄行宽点的方法。曲面曲率一般为连续的，当设计曲面局部曲率变化不大时，单点曲率可以近似描述局部曲率分布情况，主要包括最大主曲率和最小主曲率。基于刀位点处的单点曲率特征，通过试算统计、数据分析的方法，研究行宽与主曲率的关系，进而对最窄行宽点的位置做出预测。

3 试算步骤

基于实验法，令同一刀具加工具有不同曲率特征的曲面，求解行宽并记录，试算过程如下：（1）建立刀具模型。刀具底刃为圆环面，刀具半径R为10mm，圆环面截圆半径r为1mm。（2）建立待加工曲面模型。建立若干最大主曲率和最小主曲率各不相同的待加工曲面。（3）刀具定位和刀位优化。采用中点法，通过优化前倾角和侧偏角两个变量使刀具和曲面间达到双点切触的状态，此时认为行宽达到最大。（4）计算行宽。残留高度δ设为0.01mm，并研究不同残留高度下行宽和曲率的关系。采用离散刀具法求解误差分布曲线，进而计算行宽。（5）数据记录与分析。绘制行宽-曲率的关系图，分析得出行宽与曲率的关系。为了剔除具体刀具尺寸对实验结果的影响，这里行宽指的是实际行宽占刀具直径的百分比，而曲率则是刀具半径单位化后设计曲面相对曲率。

4 行宽与主曲率的关系

4.1 行宽与最大主曲率的关系

将最小主曲率k2设为任一定值（此处设为0），最大主曲率k1从0逐渐增大到1，得出行宽w随k1的变化规律，计算结果，如图 2（a）所示。

图2行宽与最大主曲率的关系Fig.2 Relationship between Strip-width and Maximum Principal Curvature

图2 中，最大主曲率k1从0逐渐增大到1时，行宽w是一个先减小后增大的过程。当k1=0时，刀具加工平面，刀具平放，行宽等于刀具直径；随着k1的增大，刀具倾角增大，与设计曲面贴合程度降低，行宽减小；当k1继续增大接近1时，曲率半径接近于刀具半径，由于刀具倾角很大，刀具的投影椭圆近似为一个圆形，与设计曲面贴合程度较高，行宽反而增大直至与设计面完全贴合。

4.2 行宽与最小主曲率的关系

将最大主曲率k1设为任一定值（此处设为0.5），最小主曲率k2从-1逐渐增大到k1，得出行宽w随最小主曲率的变化规律，如图3所示。图3中，最小主曲率从-1逐渐增大到k1时，行宽是一个逐渐增大的过程。刀具的临界前倾角由最大主曲率决定，在最大主曲率恒定时，刀具的前倾角不随最小主曲率而改变。在最小主曲率从-1增大到最大主曲率的过程中，曲面在最小主曲率方向上从“凸”逐渐变“平”再逐渐变“凹”，刀具后沿与设计曲面的距离h逐渐减小，贴合程度逐渐增高，行宽逐渐增大。当最小主曲率等于最大主曲率时，刀具底刃与设计曲面完全贴合，行宽等于刀具直径。

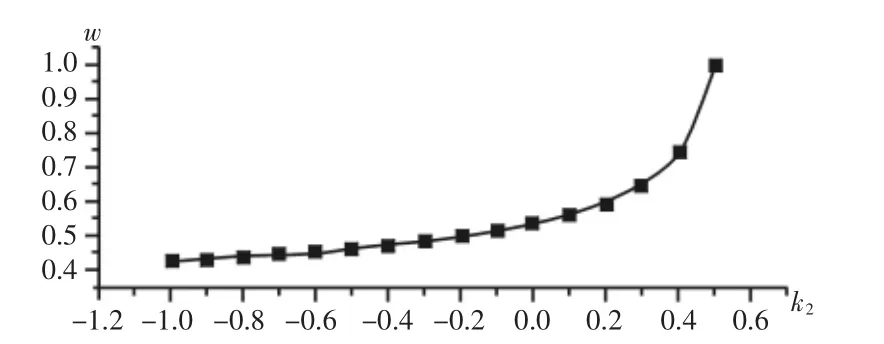
图3 行宽与最小主曲率的关系Fig.3 Relationship between Strip-width and Minimum Principal Curvature

5 基于主曲率的最窄行宽点预测

5.1 最窄行宽点预测

主曲率的取值范围为三角区域，如图4所示。该区域中又分为3块区域分别对应凹椭圆点、凸椭圆点和双曲点。采样若干曲率特征点，针对每个曲率特征点设计具有不同最大主曲率和最小主曲率的设计曲面。计算每一个曲率特征点对应的行宽，最终得到行宽w和最大主曲率k1、最小主曲率k2的等值线云图，如图5所示。

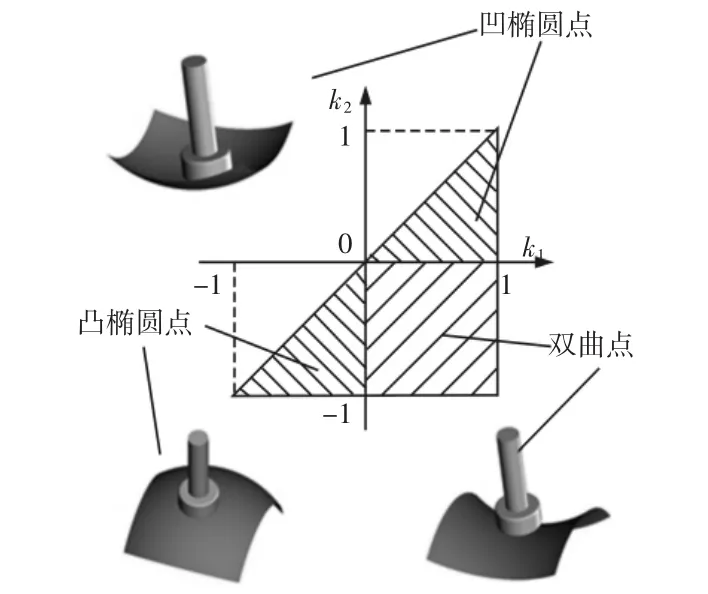
图4 主曲率的取值范围Fig.4 Range of the Value of Principal Curvature

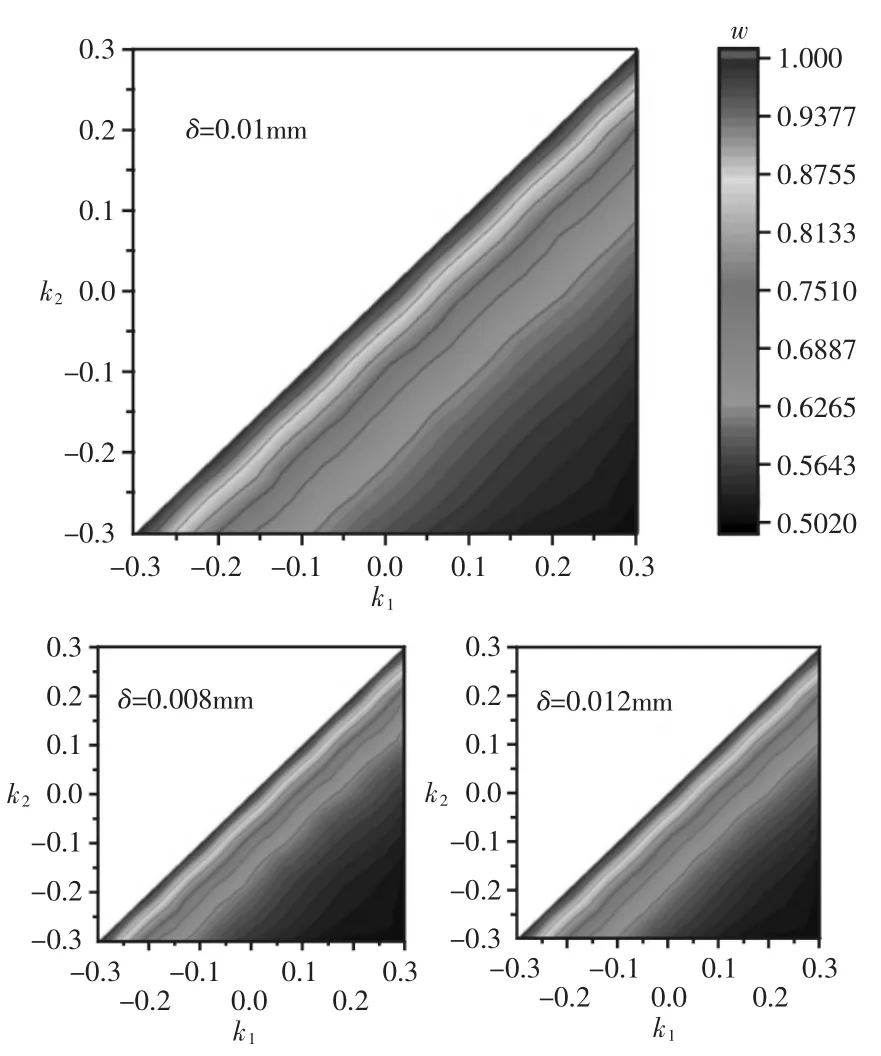
图5 行宽在主曲率坐标系中的等值线云图Fig.5 Contour Map of Strip-width in Principal Curvatures Coordinate System

通过图5中绘制的k1，k2∈［-0.3，0.3］范围内行宽的等值线图可以得到如下规律：在k1-k2坐标系内，在k1，k2接近于0的区域内，w沿近似斜45°方向递减，且在不同残留高度啄下这一规律依然成立。据此得到如下结论：在主曲率较为平坦的区域内（k1，k2∈［-0.3，0.3］），令 驻k=k1-k2，驻k 越大，行宽 w 越小，因此 驻k 最大的刀位点即为最窄行宽点。

5.2 实例验证

采用一模具曲面作为计算对象，该曲面的主曲率k1，k2∈［0，1.7］，在图5所示的［-0.3，0.3］区间内。在曲面上采样若干刀位点，并获取k1，k2，按照第3节的试算步骤计算行宽。计算结束后得到各刀位点的行宽w与主曲率差值驻k，将其绘制成散点图，如图6所示。

图6 模具型面计算实例Fig.6 An Example of Mold Surface Calculation

从图中可以看出，对于采样的若干刀位点，主曲率差值驻k越大，行宽w越小。正如在5.1节中得出的结论，在k1，k2坐标系中，如图5（b）所示．行宽w的等高线为斜45°且向右下方递减，每个驻k的值代表着一条等高线。当驻k＝0时，在k1＝k2这条等高线上，由于两个方向的主曲率相等，刀具可以完全贴合曲面，行宽最大。随着驻k逐渐增大，最大最小主曲率差值越大，等高线逐渐向右下方偏移，行宽逐渐减小。因此图6的散点图验证了当设计曲面相对平坦时，w与驻k呈负相关，刀位点处曲面的驻k越大，行宽w越窄的结论，这为日后曲面上最窄行宽点的预测提供了依据。

6 结论

（1）通过理论分析得出刀具曲面与设计曲面间的误差分布是由刀位点附近处的局部曲率分布决定的。（2）分析了行宽与主曲率的关系：当最小主曲率一定时，随着最大主曲率的增大，行宽先减小后增大；当最大主曲率一定时，随着最小主曲率的增大，行宽增大。（3）在主曲率坐标系内绘制了行宽的等值线云图，通过该图得出了在主曲率较小的区域内行宽沿近似斜45°方向递减的规律。根据这一规律得到最窄行宽点的预测方法：当设计曲面相对平坦时，行宽与最大主曲率与最小主曲率的差值呈负相关，因此主曲率差值最大的刀位点即为最窄行宽点。并通过实例验证了上述结论。鉴于研究主体为单点主曲率与行宽的关系，因此所提方法适用于局部曲率变化不大的曲面的行宽预测。这里的方法对于解决曲率变化丰富的曲面的行宽的预测问题存在一定限制，该问题将作为后续研究问题。