精密钢球传动组合行星盘误差对弹性转角影响分析

2020-03-30安子军王清华

机械设计与制造 2020年1期

安子军，姜威，张悦，王清华

（燕山大学机械工程学院，河北秦皇岛 066004）

1 引言

随着高精密机械的发展，精密钢球传动装置逐渐成为研究的热点。其在高精密机床的精确定位、航空遥感相机的位移补偿精密机构中有广泛的应用前景[1-2]。实时无隙精密钢球传动组合行星盘能够代替传统的消隙结构，实现实时消隙的功能，周向保持同步旋转，轴向利用钢球滚动特性实现轴向位移，从而能够实时消隙，满足精密机械的传动要求，因此受到学者们的广泛关注。

文献[3]根据啮合点处变形与法向力之间的非线性关系推导法向力计算公式；文献[4]运用蒙特卡洛模拟法对摆线钢球减速器传动误差进行了分析；精密钢球传动具有无侧隙、无回差的优点，其主要误差来源于弹性回差[5-6]，这与摆线针轮的传动机构有所不同[7]；文献[8-9]对双摆线钢球减速器进行了pro/E建模并进行了振动分析；文献[10]在结构原理、力学性能、运动学和动力学方面进行了一系列的研究；文献[11]对等速输出机构进行了设计与分析。但目前尚未有文献对于组合行星盘结构在受载时的弹性转角进行研究，更未对组合行星盘接触点的误差进行研究。在考虑组合行星盘误差影响的情况下，通过对实际接触角的计算，进而推导弹性转角精确表达式，研究了导向槽尺寸误差、导向钢球尺寸误差和导向槽分布圆径向误差对弹性转角的变化规律，分析了误差对转角变化率的影响。

2 结构及传动原理

实时无隙精密钢球减速器，如图1所示。中心盘右侧加工齿数为Z1的外摆线封闭槽，行星盘a的左侧加工齿数为Z2的内摆线封闭槽，且满足关系Z2-Z1=2。在内摆线和外摆线交错的区域等距装有数量为Zm的钢球，而且满足齿数关系Zm=（Z2+Z1）/2。行星盘a和行星盘b之间装有碟簧，其二者连接处均布6个圆柱槽，每个槽中放置2个导向钢球，行星盘a、行星盘b、碟簧和导向钢球构成组合行星盘。行星盘b的右侧和输出轴左侧均布相同个数的环形槽，环形槽内装有等速钢球。

减速器运转时，输入偏心轴带动组合行星盘运动，组合行星盘带动减速钢球转动，减速钢球在中心盘的摆线槽作用下，反推行星盘a以一个较低的角速度转动，实现减速运动，行星盘b在导向钢球的作用下，与行星盘a以相同的角速度转动，行星盘b通过等速钢球将速度传递给输出轴，实现等速输出。行星盘a与行星盘b之间放置碟簧，在预紧力作用下时刻处于压缩状态，可以实现减速器实时无隙啮合传动。

图1 实时无隙精密钢球减速器结构图Fig.1 The Sketching of the Real-time Non-clearance Precision Ball Transmission

3 误差模型建立

导向钢球在导向槽内为纯滚动，摩擦力较小，受力分析中忽略各接触部分的摩擦力。在求解弹性转角的过程中，导向钢球与导向槽的实际接触角是一个重要参数，因此在计算弹性转角之前必须对实际接触角进行计算。组合行星盘中，导向钢球与组合行星盘接触为空间赫兹接触，因组合行星盘轴向固定，可将接触点所在平面单独分析。以行星盘b右端面所在平面为分析平面，对组合行星盘整体进行受力分析，在考虑导向槽分布圆径向误差e3i（i=1，2，3，4，5，6分别对应 6 个导向槽）的情况下，各个导向钢球受力不同，如图2（a）所示；在考虑导向槽尺寸误差e1i、导向钢球尺寸误差e2i的情况下，以单个导向钢球啮合点所在平面对导向钢球进行受力分析，如图2（b）所示。Oin是内导向槽圆心，Oe是外导向槽圆心，假设外导向槽固定，Oii是受载之后内导向槽的圆心。

在进行计算之前引入如下假设：（1）e1i的变化仅影响相应的导向槽径向尺寸，导向槽仍保持圆柱形；（2）e2i的变化仅影响相应的导向钢球半径的大小，钢球仍然保持球形；（3）受力变形在弹性变形范围内；（4）同一导向槽内两钢球完全相同。

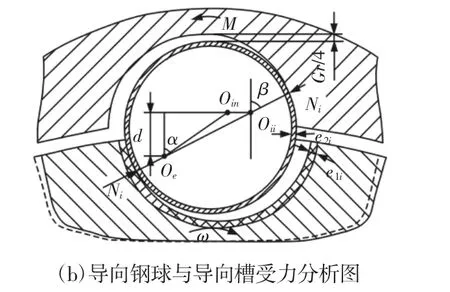
图2 组合行星盘受力分析图Fig.2 The Force Analysis of the Combined Planetary Plate

3.1 接触角误差模型

3.1.1 初始接触角

导向钢球受载前，当滚动体与导向槽刚接触时，任意滚动体位置接触对的内外圈曲率中心OinOe之间的距离为：

式中：Dq—导向钢球直径；r1i，r2i—内外导向槽半径。

此时为初始接触角琢，其计算公式[12]为：

式中：Gr—径向游隙。

3.1.2 实际接触角

在受载之后，此时的导向钢球在外载荷的作用下，接触角变为β，与初始接触角相比会发生变化。此时任意钢球位置接触对内外圈曲率中心OiiOe之间的距离为：

导向钢球与内外滚道接触，其啮合点的变形量分别为δi，法向力分别为 Ni，刚度系数[13]为 ki：

图3 接触物体主平面和主曲率图Fig.3 Main Plan and Main Curvature of the Object in Contact

法向力、接触变形和刚度系数密切相关[13]，其非线性关系为：

法向力力臂与导向钢球分布圆半径的关系由三角函数关系可以表示为：

式中：L—导向槽分布圆半径。

组合行星盘的力矩平衡方程为：

式中：M—组合行星盘所受阻力矩。

联立方程（2）～（8），整理得到：

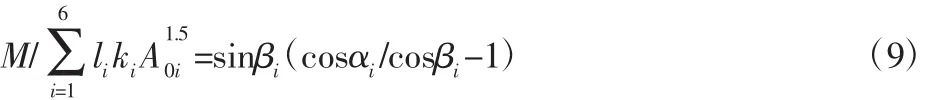
式（9）中只包含β一个未知数，通过计算便可求出受载之后的实际接触角β。

3.2 误差弹性转角模型

行星盘a顺时针转动，行星盘b受到阻力矩M的作用，在其啮合点处会产生弹性变形，使得行星盘b的实际转角相对于行星盘a的转角滞后的角度为驻α，变形协调方程为：

在考虑误差情况下，带有误差的导向钢球的载荷均不相同，如图4所示。设1号导向槽内的钢球存在负误差，其余钢球均无误差。在阻力矩M作用下，无误差钢球受挤压变形，若该变形量小于负误差值，则负误差钢球不受力，故计算组合行星盘弹性转角时不计负误差钢球，如图4（a）所示；若该变形量大于负误差值，则两类钢球同时受力，如图4（b）所示。

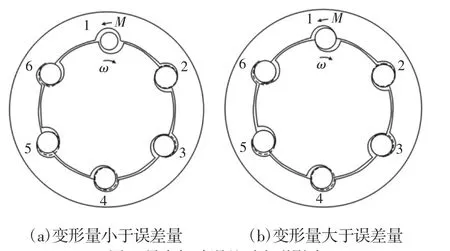
图4 导向钢球误差对变形影响Fig.4 Influence of Errors of the Ball to Deformation

另外误差的存在对于刚度系数，变形系数都会有影响，每个误差钢球所受的载荷取决于误差的大小，但是整体必须满足平衡方程。所以在综合考虑导向槽尺寸误差、导向钢球尺寸误差以及导向槽径向误差之后，推得变形协调方程为：

联立式（4）～式（8）、式（10）和式（11），整理得到新的平衡方程为：

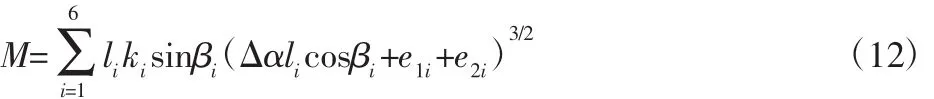
式（11）和式（12）构成的非线性方程组是以驻α为未知数，当阻力矩M给定时，依靠MATLAB的fsolve命令进行求解即可得到精确的数值。

3.3 误差灵敏度

为更直观对比各个误差对弹性转角变化的影响，基于参数灵敏度[14-15]的计算的方法，直接对各个误差求偏导，偏导数的大小即可反应弹性转角变化速度。导向槽尺寸误差、导向钢球尺寸误差、导向槽径向误差的灵敏度分别为：

4 误差影响分析

4.1 误差对弹性转角影响分析

导向槽尺寸误差e1i、导向钢球尺寸误差e2i和导向槽分布圆径向误差e3i对实际接触角βt和弹性转角驻α均有影响。根据样机参数，导向钢球分布圆半径L=14.25mm，导向钢球半径rq=1mm，导向钢球数 Zm=12，阻力矩 M=15N·m。e1i、e2i和 e3i对于实际接触角和弹性转角的影响，如图5～图7所示。

图5 导向槽尺寸误差影响图Fig.5 Influence of the Size Errors of the Guide Groove

图6 导向钢球尺寸误差影响图Fig.6 Influence of the Size Errors of the Ball

图7导向槽分布圆径向误差影响图Fig.7 Influence of the Radial Errors of Guide Groove Distribution Circle

图5 （a）中，实际接触角随着导向槽尺寸误差e3i的增大而减小，其减小的速度呈现减缓的趋势，最大数值为1.0994rad，最小为1.0763rad；图5（b）中，弹性转角随着e3i的增大而增大，增大的速度逐渐减慢，e3i过大会导致组合行星盘的弹性转角过大，影响机构的精密性，过小则可能出现钢球无法安装的问题，弹性转角最大值为6.5301×10-4rad，最小值为 6.3045×10-4rad。图 6（a）中，实际接触角随着导向钢球尺寸误差e2i的增大而增大，其增加的速度也随着误差的增大而增大，最大数值为1.0991rad，最小为1.0764rad；图6（b）中，弹性转角整体上随着e2i的增大而减小，而且减小的幅度越来越大，曲线整体分为两段，在［-0.01，-0.006］时，由于弹性转角小于误差量，此时的导向钢球并没有与导向槽啮合，因此该区间内，实际接触角为 0，弹性转角为定值，在（-0.006，0.01］时，弹性转角的减小速度随着误差的增大而逐渐增大，e2i过大虽然弹性转角会减小，但是此时的钢球可能会和导向槽出现过盈配合，无法安装，e2i过小时，误差钢球在组合行星盘当中没有发挥应有的作用，导致弹性转角过大。

从图7中曲线变化可以看出，实际接触角和弹性转角均随着导向槽分布圆径向误差e3i的增大而减小，但图7（a）的纵坐标几乎没有变化，说明e3i对于实际接触角的影响非常小，图7（b）弹性转角在整个误差范围内仅减小了0.0026×10-4rad，可见e3i对于组合行星盘的影响很小。