电动车再生制动系统的仿真及试验研究
2020-03-28王茹洁武志斐
王茹洁,武志斐
(太原理工大学车辆工程系,山西 太原 030024)
1 引言
电动自行车是一种在城市广泛应用的新型自行车,由于行驶环境的特殊性,制动较频繁,现有研究表明:在城市工况下,小型车辆在制动过程中消耗的制动能量约占总驱动能量的50%[1]。电动自行车具有能量来源可持续、零排放、轻巧便捷等优点,逐渐成为研究热点,但蓄电池充电时间长、续驶里程短等因素限制了电动自行车的推广。目前,最需解决的问题是提高电动自行车的续驶里程。
文献[2]分析了再生制动回收系统的可行性,试验研究表明加装制动回收系统的电动车在单次充满电后提高行驶里程(5~20)%。
为解决试验车续驶里程不足问题,文献[3]将ADVISOR原有策略与模糊控制策略进行对比,得出后者回收率策略优于前者。文献[4]针对前后轴制动力保持固定的混合系统,提出了一种电机与机械制动力分配的优化方法,得出制动能量回收率比模糊控制多16%。文献[5]采用电机和带ABS的并联制动方式,得到能量回收效率为42.7%,但此方法复杂,只有改变制动状态才能回收能量。文献[6]将理想制动力I曲线和ECE法规结合进行制动力优化分配,得出制动回收效率为24%。
针对富士达电动自行车,在Matlab/Simulink中建立模糊控制策略模型进行仿真;搭建试验台架并测试试验车在紧急制动、中轻度制动及下长坡制动三种工况下回收的能量,比较分析试验结果与仿真结果,验证试验的可行性。
2 电动自行车再生制动原理
电动自行车在制动过程中,车轮与路面之间摩擦生热消耗部分制动能量,若将这部分能量回收利用,可增加试验车的续驶里程。
当前后轮同时抱死,同步附着系数等于制动强度。Fbf、Fbr[7]为前后轮总的制动力,公式如下:

式中:φ—路面附着系数;z—制动强度;Fz1、Fz2—前后轮的法向反作用力,N;Fb—总制动力,N。

式中:a—前轮距质心的距离,m;b—后轮距质心的距离,m;L—前、后轮之间的距离,m;hg—质心高度,m。
β[8]定义为驱动轮的制动力与总制动力的比值,如下式所示:

式中:Fre—后轮的再生制动力,N。
电机额定功率范围内,回收的能量为下式:

式中:T—电机转矩,N·m;n—电机转速,r/min;η—电机效率。
制动能量回收率η可反映回收的能量,如下:

式中:Ec—电容回收的能量,J;ω1—制动初始速度,rad/s;ω2—制动终了速度,rad/s。
3 基于模糊控制的制动力分配
制动过程中,采取不同类型的控制策略分配制动力,会产生不同的能量回收效果。为了更佳的分配机械制动力与再生制动力,确保前后轮协调配合,高效运行,选取模糊控制策略[9-10]。
3.1 模糊控制总体结构
模糊控制器的总体结构,如图1所示。由图知,输入量为:制动强度、蓄电池SOC、电机转速n;输出量为再生制动力占总制动力的比值k。

图1 模糊控制器结构Fig.1 Fuzzy Controller Structure
3.2 模糊控制器设计
首先,确定模糊控制器三个输入量和输出量的模糊子集都为{high,middle,low}。n的论域为[-1,1],制动强度和 SOC 模糊论域为[0,1]。隶属度函数均为高斯型,输入、输出量的分布,如图2所示。

图2 制动强度z、蓄电池SOC、电机转速n和再生制动力占总制动力比值K的隶属度函数Fig.2 The Membership Function of the Brake Strength z,Battery SOC,Motor Speed n and Regenerative Braking Force in Total Braking Force Ratio K
然后,根据模糊变量之间的关系表示出模糊控制规则,将其导入计算机内控制再生制动力的比值。最后,将模糊输出量进行解模糊化,采用加权平均法,即:

式中:βi—第i条规则输出结果;Ki—在第i条规则中电机制动力所占比例;K—总输出量。
再生制动力所占比值k与z、SOC以及n之间的关系如图3所示。由图 3(a)知,当 z减小,n 增大时,k 逐渐增大;由图 3(b)知,当z和SOC都减小时,k逐渐增大;由图3(c)知,当soc减小,n增大时,再生制动比例k逐渐增大。由此可知,z减小,SOC减小,n增大,k值就增大。z>0.4,soc>0.4,n>-0.5 时,k基本保持在0.5附近。
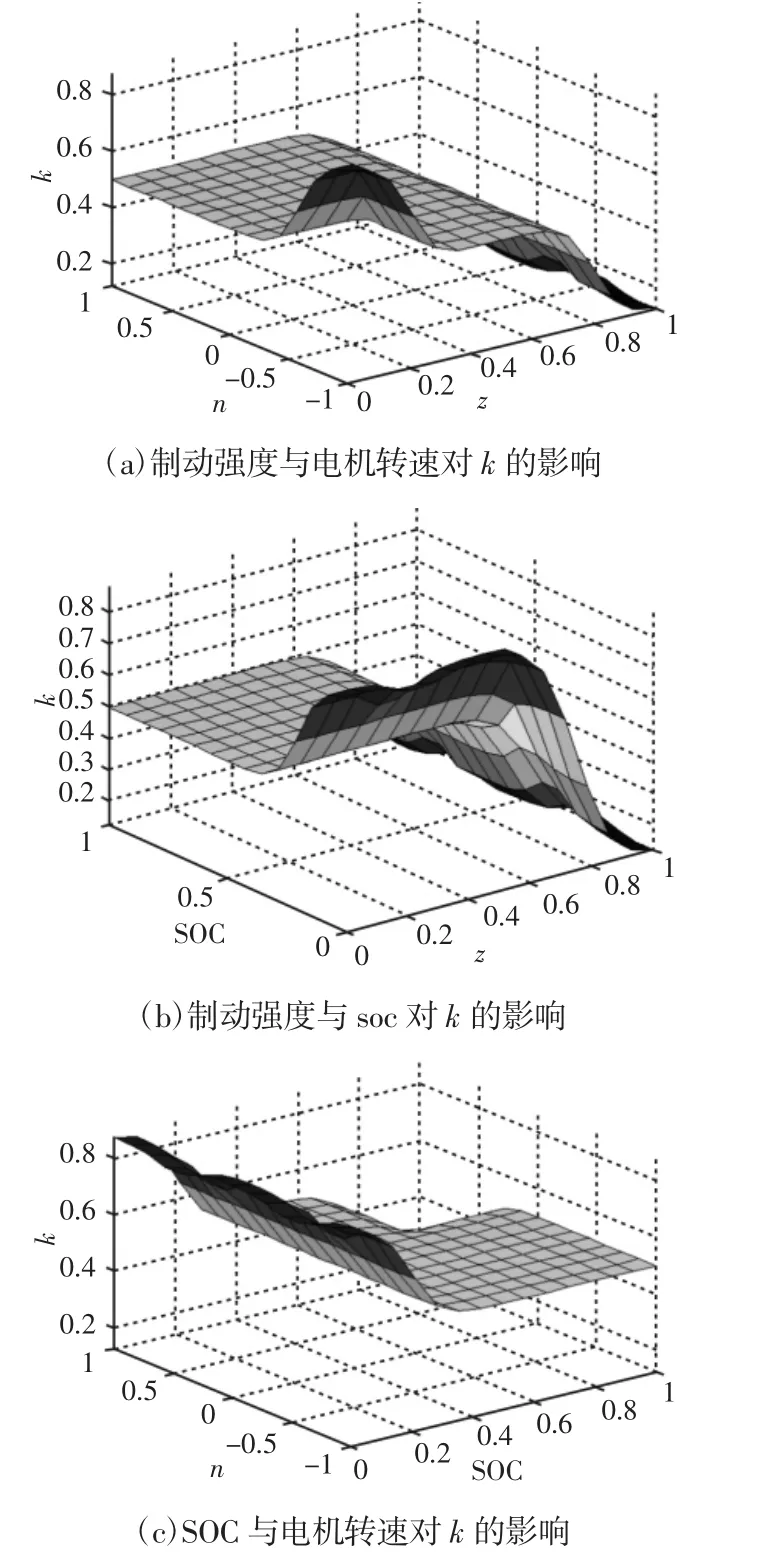
图3 z、SOC、n与k的关系Fig.3 The Relationship Between z、SOC、N and k
4 试验台架设计
4.1 试验台总体结构
试验台零部件包括:富士达电动自行车,45齿和15齿链轮,传动轴,带座轴承,电磁离合器,12V蓄电池,发电机,整流器(6只二极管组成),超级电容及220Ω电阻。试验车参数,如表1所示。

表1 电动自行车参数Tab.1 Electric Bicycle Parameters
制动过程中,放开转把,电磁离合器与12V蓄电池立即接通,使得离合器左右两侧吸合,将驱动轮的动能传递给发电机来回收电能;加速过程中,转动转把,电磁离合器与蓄电池断开,不回收能量。台架模型,如图4所示。
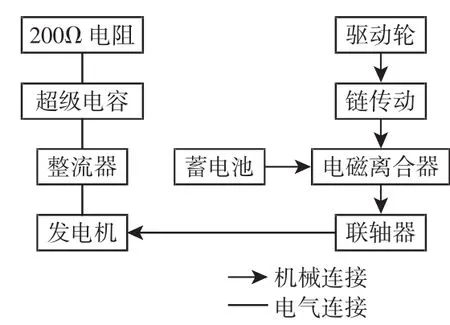
图4 台架模型Fig.4 Bench Model
为了直观的表示制动过程中回收的能量,首先将45齿链轮固定在自行车后轮上,通过链传动传递给15齿链轮,带动电磁离合器一侧转动;然后接通蓄电池,使电磁离合器两侧吸合,通过联轴器将动能传递给发电机;最后发电机将动能转化为电能存储到超级电容。
4.2 试验台工作原理
试验台是在试验车的基础上进行改进和扩充,目标是测试多种工况下能量回收性能,为优化控制策略提供良好的试验平台。
电动自行车转把转角可分为三等分,分别代表高速、中速和低速,以此来模拟紧急制动、中轻度制动和下长坡制动工况。当转把转到某一工况时,松开转把,接通12V蓄电池,驱动轮将惯性能通过链传动传递给发电机,再经整流器将不稳定的交流电转变为直流电,回收到超级电容中。分别测量三种工况下超级电容两端电压及驱动轮转速,电压用TBS1064示波器测量,转速用无线扭矩节点测量,如图5、图6所示。

图5 超级电容两端电压Fig.5 Super Capacitor Voltage

图6 电动自行车驱动轮转速Fig.6 Speed of Driving Wheel of Electric Bicycle
制动过程中,驱动轮五秒左右停止,超级电容由于充放电时间短作为储能装置,而仿真过程将电池作为储能装置。试验过程没有考虑车轮与路面之间的摩擦,主要是为了验证制动惯性能量转化为电能的最大效率。机械制动力主要是轮毂电机内部摩擦产生,再生制动力由发电机产生。
制动结束时,超级电容两端的电压在三种工况下分别为10.2V、7.4V和2.6V;驱动轮转速分别为399r/min、315r/min和224r/min。三种工况下最大制动强度z分别为0.7020、0.2161、0.4412,中轻度制动工况下z最小,则再生制动力所占比例最小。
5 仿真与试验结果分析
5.1 simulink模型
为验证控制策略可行性,在Matlab/Simulink中建立控制模型,如图7所示。在确保安全性和可靠性的同时,合理分配试验车两个轮的再生制动力与机械制动力,提高能量回收效率。
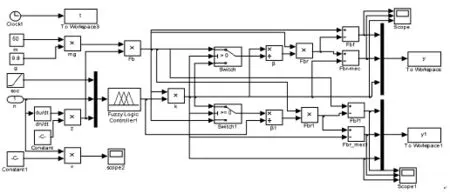
图7 simulink模糊控制模型Fig.7 Simulink Fuzzy Control Model
试验车自定义三种工况,即紧急制动、中轻度制动、下长坡制动,制动初始速度分别为7.445m/s、5.861m/s、4.169m/s。分别对三种工况进行仿真验证,得出电池SOC提升了3.22%、1.56%、0.36%。
5.2 比较分析
试验车仿真与试验能量回收效果,如表2所示。由此可知,在紧急制动、中轻度制动、下长坡制动三种工况下,仿真的能量回收率分别高于试验2.85%、1.54%、2.48%。因为试验过程中链条自重消耗能量较多,导致能量回收效果低。其中,安装在后轮的链轮质量为2.3kg,半径为0.116 m。

表2 试验车能量回收效果对比Tab.2 Comparison of Test Vehicle Energy Recovery
6 结论
根据再生制动原理,选取模糊控制策略来分配试验车前后轮的机械制动力和再生制动力,并在MATLAB/simulink中进行仿真;然后用富士达自行车搭建实验台架,将不同工况下制动初始的惯性能通过链传动传递给发电机,再将能量存储到超级电容中进行验证;最后,对比分析紧急制动、中轻度制动、下长坡制动三种工况下的能量回收率,仿真结果分别高出试验2.85%、1.54%、2.48%。
